立足数学实验 指向核心素养——“展开与折叠”教学设计与思考

■刘春阳

一、理论支撑

1.数学实验活动。数学活动经验的积累是提高学生数学素养的重要标志。帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果。

2.数学核心素养。数学核心素养是数学学习者在学习数学某一个领域所表达出的综合性能力。初中数学课程应该培养学生需要具备的核心素养有数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等。

二、教学目标

通过展开、折叠，感受立体图形与平面图形之间的关系；有些立体图形按照不同方式展开成平面图形,有些平面图形也可以折叠成立体图形；能想象并画出简单几何体的表面展开图,能根据表面展开图判断、制作简单几何体；经历、体验图形的变化过程,发展空间观念,养成研究性学习的良好习惯。

三、教学重、难点

1.教学重点。通过展开、折叠，感受立体图形与平面图形之间的关系，体验图形的变化过程，发展空间观念。

2.教学难点。能想象并画出简单几何体的表面展开图，能根据表面展开图判断、制作简单几何体。

四、教学设计

活动一：圆柱的侧面展开图。

1.图片展示，引导学生观察图片中的建筑物，探寻学过的几何图形——圆柱体。

引导学生结合圆柱体模型，分组讨论下列问题：

问题1：怎么求圆柱体的侧面积？

问题2：圆柱体侧面展开会是什么图形？

讨论结束后，先请一位学生演示：沿图1的虚线剪开，展开，观察所得图形，再探究它与立体图形之间存在的数量关系。

图1

图2

设计意图：从建筑物着手，抽象出几何图形，作为新知识的生长点，提出问题，引导学生思考。学生能真切感受到数学来源于生活，又服务于生活。培养学生应用数学的意识。圆柱体的侧面是曲面，其面积不容易计算，采取的策略是将曲面平面化，把不能直接解决的问题，通过转化，变成可以用已有的知识或经验来解决的问题，培养学生的转化思想。

2.教师引导学生思考。

问题3：将圆柱体的侧面沿不同的路线剪开，展开，所得到的平面图形是否相同？

问题4：这些平面图形之间有什么关系？

学生按照自己设计的路线（如图2）剪开，并展开成平面图形，在小组内讨论，得出结论：将圆柱体的侧面沿不同的路线剪开，展开所得到的平面图形不相同，但是这些图形经过变换后，都可以得到第一种图形——长方形。得出圆柱的侧面展开图之间的关系：

立体图形（侧面）平面图形

数量：1.圆柱底面圆的周长等于长方形的长；

2.圆柱的高等于长方形的宽；

3.圆柱侧面积等于长方形的面积。

思想方法：转化思想。

设计意图：让学生经历展开与折叠的全过程，体会立体图与平面图形之间的关系，增强空间想象能力；让学生明白展开与折叠都是解决问题的办法，体会转化思想；让学生设计出不同的路线，剪开，展开，有助于培养学生设计问题的能力和创新意识，同时又能增强学生做数学实验的操作能力。先从“数量”角度探究剪的图形与长方形之间存在相等关系，进而启发学生思考：从“形”的角度看，它们之间会不会存在着某种必然的联系？体现了“数形结合”的数学思想。多样化的展开方式有较强的创新性，同时也体现了图形的内在统一性。创新意识是学生核心素养中的核心，培养学生的创新意识，数学教学有不可替代的作用和价值。

活动二：圆锥的侧面展开图。

实物展示：在日常生活中，有些建筑物可以抽象成圆锥体。仿照研究圆柱体侧面展开图的方法，探究圆锥的侧面展开图。

图3

图4

问题5：怎么计算圆锥的侧面积?圆锥体侧面展开又会是怎样的图形呢？

操作：请一名学生演示，将圆锥侧面沿如图4的虚线剪开，展开，然后，其他同学各自将课桌上的圆锥侧面沿虚线剪开，展开，再将其卷起作为圆锥的侧面，反复操作。

探究它们之间的数量关系：

立体图形（侧面）平面图形

数量：1.圆锥底面圆的周长等于扇形的弧长；

2.圆锥的侧面积等于扇形的面积；

3.圆锥母线等于扇形的半径。

思想方法：转化思想

设计意图：数学教学的实质就是教会学生提出问题、思考问题和探究解决问题的方法。因为圆柱体和圆锥的侧面都是曲面，所以探究圆锥的侧面和扇形之间的“数”与“形”的关系就完全可以借助探究圆柱体侧面的方法，放手让学生自主完成。用类比的方法去学习新知识，发现新结论，是数学学习中重要的方法。学会学习是学生核心素养的重要组成部分。这部分教学设计是为了进一步增强学生对圆柱体与扇形的空间意识和实践操作能力，引导学生勤思考、善归纳、会总结，提升学生数学学习素养。

活动三：正方体的侧面展开图。

实物展示：如果一个几何体的表面是平面，它的表面展开图会是什么样呢？我们以正方体为例，探究正方体沿部分棱剪开、展开所得到的图形。

问题6:将一个正方体纸盒沿部分棱剪开，展开，会得到什么样的平面图形呢?

问题7:将一个正方体纸盒沿部分棱剪开并展开得到平面图形，至少需要剪开几条棱?

（要求:正方体表面展开成的6个正方形要相连，即其中每个正方形至少要有一条边与其他的正方形的边重合。）

设计意图：正方体的6个面都是平面，通过动手操作，让学生感悟到同一个正方体纸盒的表面沿不同的棱剪开，展开成的平面图形不相同。让学生经历从独立操作到交流分享的过程，培养其合作学习的习惯和意识。

教师在学生剪出的图形中任选一种引导学生思考：

问题8：你怎样得到如图所示的平面图形？

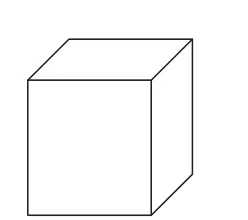
图5

学生分组讨论并解释如何操作，对于难点问题，可展开讨论。

设计意图：根据要求展开正方体纸盒，目的是要求学生将操作与思考结合起来。如何剪？这样剪行吗？下一步又怎么剪？定向剪裁的展开方式是本课的难点，对学生的空间想象能力要求较高。动手操作和动画演示相结合，可以较好地培养学生的空间想象能力，有助于培养学生的空间观念，把数学核心素养的养成落实到每一节课上。

在问题8的基础上，教师利用几何画板把刚才的动画逆向演示，将其折叠可以得到正方体，提出下面问题：

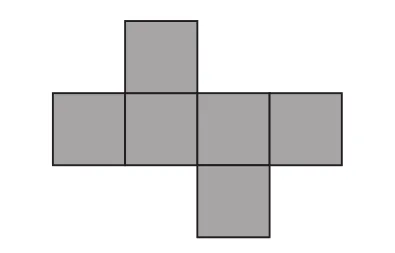
问题9：下面图形能折叠成正方体吗?若能，请指出相对面。

设计意图：“先想一想，再折一折”是一个观察、思考、实践的过程，其中“想一想”是理性的思考，有助于提高学生的空间想象能力，“折一折”是操作活动，可以让学生直接感受平面图形与立体图形之间的关系，并验证“猜想”是否正确，有助于培养学生的空间观念。

问题10：下面图形能折叠成正方体吗？若不能,怎样改变其中一个正方形的位置，使它与其余5个小正方形重新拼接后能折叠成正方体？

教师可让一个学生到讲台前操作，并思考：可移动的正方形有几个？移动一个正方形后，将其摆放的位置有几处？

设计意图：通过观察、思考，学生能够发现，图示的平面图形不能沿虚线折叠成一个正方体，通过平移可以改变形状，使之可以折成一个正方体。这样既锻炼学生的实际操作能力，又发展学生的空间想象能力。可移动的正方形有3个，移动一个正方形后将其摆放的位置有4处，又强化学生的分类思想。提醒学生要从多角度思考问题，考虑问题要全面。

思考：把下列图形沿虚线折叠，观察其围成的几何体。

设计意图：把所给的图形沿虚线折叠，并加以判断，这一过程突出了学生的自主操作，引导学生再次感知：平面图形和立体图形可以通过折叠和展开相互转化，并解决有关实际问题和数学问题，进一步渗透转化思想，提高学生解决问题的能力。

五、教学反思

1.数学活动经验是提升数学思维的支撑。

《全日制义务教育数学课程标准（2011年版）》特别强调，数学活动经验的积累是提高学生数学素养的重要标志。帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动的结果。“数学活动经验”是在“做”中积累起来的，因此在教学中，我让学生亲身参与了“剪一剪”“展一展”“折一折”“拼一拼”等活动，让学生在获得丰富的活动经验的同时，又经历了探究、思考、抽象、归纳等数学思维的全过程，既达到对展开与折叠的过程体会，又让学生真正明白展开与折叠是解决数学问题的有效办法。这样既能增强学生的数学直观能力，又能让学生感悟到数学的理性思维。数学活动经验是学生思考和创新的起点，是核心素养形成的有效支撑。

2.高质量问题是数学教学的核心。

一个高质量的数学问题要能够激发学生的好奇心，引起学生思考，激发学生创造性的思维，启迪学生的智慧。问题3和问题4既可以引导学生从边长、面积这样的数量角度思考，也可以引导学生从“图形”本身的角度思考。当一连串的问题得到解决,学生才恍然大悟，圆柱体侧面沿不同的路线剪开，展开，得到的平面图形都可以经过变换得到长方形，因此我们在研究圆柱体的侧面展开图时，只需沿母线剪开，展开即可。在教学过程中，教师考虑到学情和数学本身的特点，不急于求成，而是紧紧抓住学生思维的闪光点追问，既突破了难点，又作为新知识的生成点，“生成”一些新的教学资源,体现了数学的实质。教师能够及时把握，因势利导,有意识地培养学生创新意识，可谓彰显了智慧，启迪了思维。

3.数学思想方法是数学核心素养的精髓。

数学思想方法是数学学科的特质，是数学区别于其他学科的重要标志。数学思想方法的掌握是提高数学思维能力的必经之路，是数学学科的核心素养，需要在教学中不断挖掘和渗透。本节课的核心数学思想方法有：转化思想、分类思想、数形结合思想。

总之，一节数学实验课只有以提升学生数学核心素养为认知目标，才是有效的、高效的、实效的课堂。