运用手持计算器对函数对称问题的探索

刘红卫 程海波 刘伯贤 雷丹 夏远景

摘 要：函数是中学数学教学的主线，是中学数学的核心内容，也是整个高中数学的基础。函数的性质是竞赛和高考的重点与热点，函数的对称性问题是函数性质的一个重要方面，也是历年高考热点问题之一，函数图像的对称性包括图像关于直线轴对称和关于点中心对称的两类问题，函数图像对称问题还分为一个函数图像的自对称问题和两个函数图像的互对称问题。图形计算器一般是指一种可以绘制函數图像、解高次方程或多元方程组以及能执行其他复杂操作的手持计算器，大多数图形计算器还能编写数学类程序。有人指出：“数学教学应该使用科技来帮助所有学生理解数学，并为在越来越科技化的社会中应用数学做好准备。”同时也要求培养学生的动手能力，提升学生发现问题、解决问题的能力。文章针对这些问题给出一般结论，并分别加以理论证明和手持计算器中的直观呈现，体现了手持计算器在数学教学下的作用和优势，以及它在教学中的应用，希望能给广大教师一定的教学启发。

关键词：图形计算器；自对称；互对称；轴对称；中心对称

中图分类号：G633.6 文献标识码：A收稿日期：2017-12-08

首先我们看看高考题或高考模拟题：

1.【2011年新课标卷文12】函数y=—的图像与函数y=2sinπx（-2≤x≤4）的图像所有交点的横坐标之和等于

（A）2 （B）4

（C）6 （D）8

解析：图像法求解。y=—的对称中心是（1，0），也是y=2sinπx（-2≤x≤4）的中心，-2≤x≤4，它们的图像在x=1的左侧有4个交点，则x=1右侧必有4个交点。不妨把它们的横坐标由小到大设为x1，x2，x3，x4，x5，x6，x7，x8，则x1+x8=x2+x7=x3+x6=x4+x5=2，所以选D。

考点：①函数图像的对称性；②数形结合思想。

2.【2014高考全国2卷文第15题】偶函数y=f（x）的图像关于直线x=2对称，f（3）=3，则f（-1）=______.

解析：因为y=f（x）的图像关于直线x=2对称，故，f（3）=f（1）=3，又因为y=f（x）是偶函数，所以f（-1）=f（1）=3，故答案为3。

考点：①函数图像的对称性；②函数周期性。

函数的对称性、周期性、奇偶性是高考的热点问题，而且多以选择题、填空题综合多个知识点同时考查，分值5分，高中学生必须理解。下面我小结了函数对称的几个性质，首先从理论上证明，培养学生的逻辑推理能力，同时用手持计算器探索、演示，可培养学生的动手能力，加强学生对知识生成的直观感受，让学生有身临其境的感觉，这是手持计算器独到的好处，也是本文的亮点。

一、同一个函数图像关于直线的对称（自对称）

结论1：设a，b均为常数，函数 y=f（x）对一切实数x都满足f（a+x）=f（b-x），则函数的图像关于直线x=—对称。

证明：在函数f（x）上任取一点P（x1，y1），即y1=f（x1），则点P关于直线x=—的对称点为Q（a+b-x1，y1），

∵f（a+x）=f（b-x），

∴f（a+b-x1）=f（a+（b-x1））=f（b-（b-x1））=f（x1）

∴y1=f（a+b-x1）

∴点Q（a+b-x1，y1）也是函数y= f（x）上的点。

∴命题得证。

下面用手持计算器直观呈现（改变a，b的值）。

（1）我们先将公式变形，将f（a+x）=f（b-x）转换为f（—+t）=f（—-t）

a+x→ —+—+x

b-x→ —-—-x

另t=—+x

a+x→ —+t

a+x→ —-t

（2）做出a，b的值，选择命令→绘图→滑动条，取最小值为-10，最大值为10，值和步长都为1，选择动画为无动画（如图1）。

同样的方法作出b的值。

（3）作出t的值，也是以滑动条的方式做出t的值，将t的值设置为来回或循环。

（4）因为函数的定义为：设在某变化过程中有两个变量x、y，如果对于x在某一范围内的每一个确定的值，y都有唯一确定的值与它对应，那么就称y是x的函数，x叫做自变量。所以任意一—+t都有一个y值与之对应，但y值是唯一确定的值。

（5）进入symb视图，选择命令→点→点，输入point（—+t，t2）。这时出现的是一个移动的点。点击屏幕，选择选项将动画前面的钩取消掉。点击点，选择选项，勾选矩阵迹。点的纵坐标t2不唯一，不同的对应关系产生不同的y值，随着t值的变化，点的位置也会变化，形成的就是某种对应关系下的函数图像（如图2）。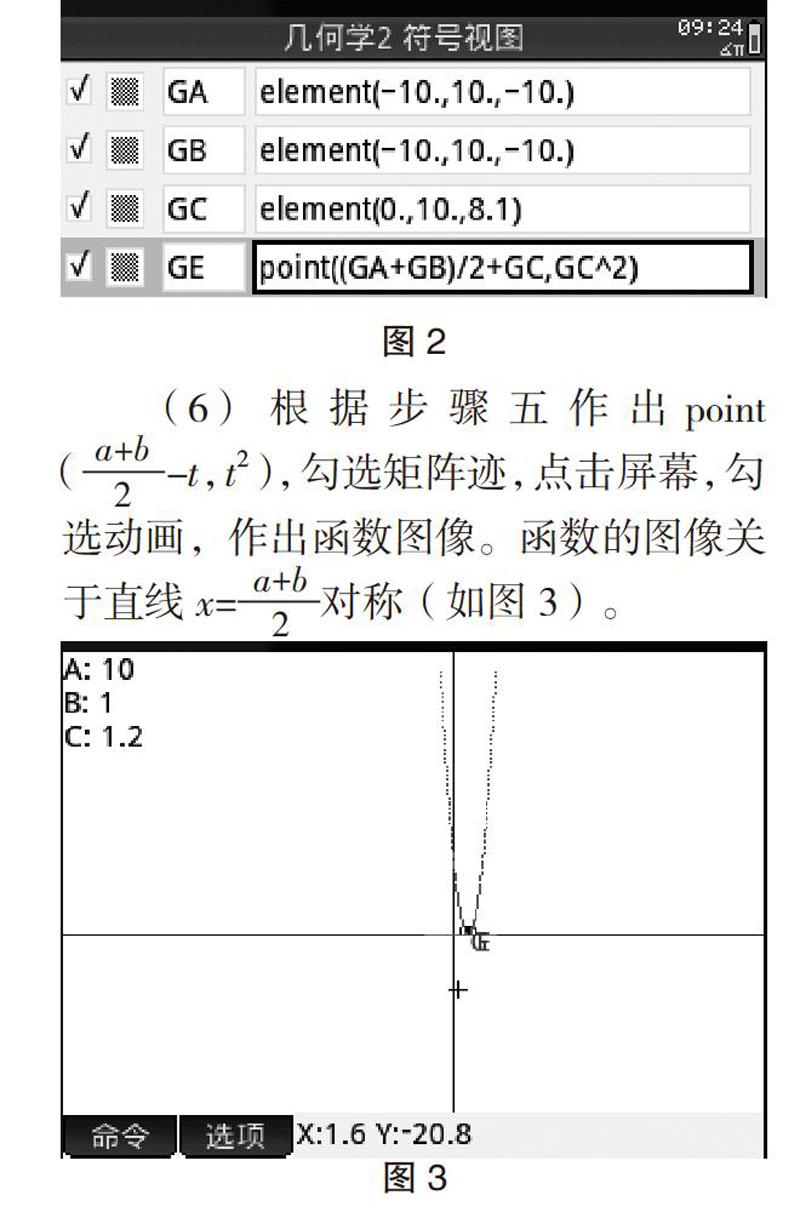

（6）根据步骤五作出point（—-t，t2），勾选矩阵迹，点击屏幕，勾选动画，作出函数图像。函数的图像关于直线x=—对称（如图3）。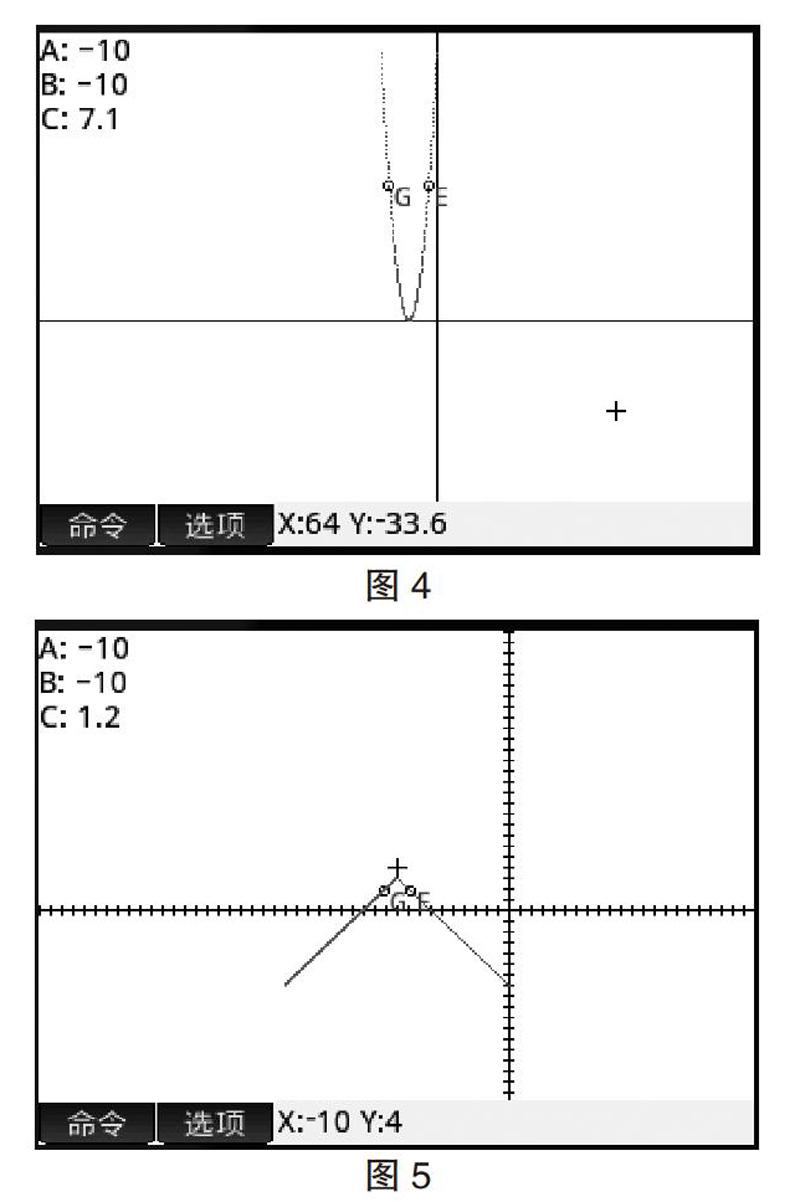

（7）我们可以改变a，b的值，作出函数的图像。点击屏幕，取消动画。改变a，b的值，点击点，选择清除矩阵迹，勾选动画（如图4）。

（8）重复步骤7，改变函数的对应关系，将t2改成3-t（如图5）。

结论成立。

推论1：在直角坐标系中，满足f（a+x）=f（a-x）的函数y= f（x）关于直线x=a对称（其中a为常数）（特例：当a=0时，若y= f（x）的定义域关于原点对称，则y= f（x）为偶函数）。

推论2：在直角坐标系中，满足f（a-x）=f（x-a）的函数y= f（x）的图像关于直线x=0对称。

二、两个函数图像关于直线的对称（互对称）

结论2：在同一直角坐标系中，函数y1=f（a+x）与函数y2=f（b-x）的图像关于直线x=—对称（其中a，b均为常数）。

证明：

方法一：已知y1，求出y1关于直线x=—对称的函数y3，若y3=y2则证明完毕。

在函数y3上任取一点P（x0，y0），即y0=f（a+x0），则点P关于直线x=—的对称点为Q（b-a-x0，y0），则点Q必在函数y1的图像上。

∴y0=f（a+（b-a-x0））=f（b-x0），即点（x0，y0）在y2=f（b-x）的图像上。

∴函数y3=y2，命题得证。

方法二：函数y1=f（a+x）的图像可以看成是函数y=f（x）的图像向左平移a个单位所得，现在函数y=f（x）图像上任取一点P（x1，y1），则点P1（x1-a，y1）在函数y1=f（a+x）的图像上；函数y2=f（b-x）的图像可以看成是函数y=f（x）的图像先关于y轴对称得y=f（-x）的图像，再向右平移b个单位得y2=f（-（x-b）），即得函数y2=f（b-x）的图像，则点P2（b-x1，y1）在函数y2=f（b-x）的图像上，又因为点P1（x1-a，y1）和点P2（b-x1，y1）关于直线对称，所以两函数图像关于直线x=—对称。命题得证。

下面用手持计算器直观呈现（改变a，b的值）。

（1）打开几何学应用程序，我们先做出一个函数，点击命令→选择绘图→函数，绘制任一函数，为之后不对结论产生误导，在这里最好绘制奇函数而非偶函数。我们可以尝试绘制函数y=x3（如图6）。

（2）已经作出函数y1=f（x）的图像，现在作出函数y1=f（a+x）的图像。先做出a值，在plot视图选择命令→绘图→滑动条，取最小值-10、最大值10、初始值为1、步长为1，其他不变（在这里取值是为了取到正数、0、负数，证明a为常数时结论满足）。在符号视图将GB改成a（如图7）。

现在我们能在plot视图看到a的值，我们将鼠标长按在a值上会出现滑动块，移动滑动块可以改变a的值（如图8）。

（3）使用同样的步骤作出b值。

（4）在symb视图做出y1=f（a+x），进入symb视图，选择命令→绘图→函数，plotfunc（a+x）3。为区分原函数和函数y1，改变函数y1的颜色（如图9、图10）。

（5）同样的方式作出y2=f（b-x）的函数图像（如图11、图12）。

（6）作出函数y1和y2的函数后，原函数不需要了，可以选中原函数的图像将函数图像隐藏。此时，我们能直观地看出两个函数图像是对称的，但函数图像是否对称还需要我们进行证明。

（7）在y1上面取一点，做直线x=—，以直线为对称轴做出点的对称点，如果对称点再函数y2上，则两函数对称。

（8）进入plot视图，选择命令→点→上面的点。进入symb视图，选择命令→线→直线line（x=—）。做出对称点，选择命令→变换→反射（如图13）。

（9）验证点G是否在函数图像上，选择命令→检验→对象上。检验结果为1，表示点在直线上。长按在点B上，进入编辑界面，将无动画改为来回或循环，发现检验结果一直为1（如图14）。

（10）也可以将点B和点G的坐标表示出来，选择命令→笛卡尔→坐标。同时也可以改变a，b的值，发现结论同样正确（如图15）。

推论1：在直角坐标系中，函数y1=f（a+x）与函数y2=f（a-x）的图像关于直线x=0对称（特例：当a=0时，函数y1=f（x）与函数y2=f（-x）的图像关于y轴对称）。

推论2：在直角坐标系中，函数y1=f（a-x）与函数y2=f（x-a）的图像关于直线x=a对称（其中a为常数）。

三、同一个函数图像关于点成中心对称

结论3：设a，b均为常数，函数对一切实数x都满足f（a+x）+f（a-x）=2b，则函数y=f（x）的图像关于点（a，b）成中心对称图形。

证明：

方法一：∵f（a+x）+f（a-x）=2b

∴[f（a+x）-b]+[f（a-x）-b]=0

令F（x）=f（a+x）-b，（x∈R）

∴F（x）+F（-x）=0，即F（x）为奇函数，其图像关于原点（0，0）对称。

∴y=f（a+x），（x∈R）的图像关于点（0，b）对称

∴y=f（x），（x∈R）的圖像关于点（a，b）成中心对称，证明完毕。

∴命题得证。

方法二：∨P（x0，y0）∈y=f（x）图像上，从而有y0=f（x0），

则可得P（x0，y0）关于点（a，b）对称的点Q（2a-x0，2b-y0）。

下面证明点Q在y=f（x）上，即证2b-y0=f（2a-x0），

需证f（2a-x0）+f（x0）<=>f（a+（a-x0））+f（a-（a-x0））=2b。

这里显然成立（只需令x=a-x0即可）

由于P点的任意性可知y=f（x）关于点（a，b）对称。证明完毕。

下面用手持计算器直观呈现（改变a，b的值）。

（1）本结论为结论1的引申，我们在结论1的方法上证明。使f（a+x）的值为b+x，f（a-x）的值为b-x。将结论一的point（—+GC，GC2）改为point（GA+GC，GB+GC2），point（—-GC，GC2）改为（GA-GC，GB-GC2）（如图16）。

得出函数图像（如图17）：

（2）函数图像作出来之后，点击选项，取消动画。连接两点做一条线段，取中点，选择命令→线→线段→选择点G和点E，再选择命令→点→中点→选择点G和点E。勾选动画（如图18）。

点G点E关于点H对称，点H位置不变，所以函数关于点H（a，b）成中心对称图形。

推论：设a，b，c均为常数，函数y=f（x）对一切实数x都满足f（a+x）+f（b-x）=2c，则函数y=f（x）的图像关于点（—，c）成中心对称图形（特例：当a=b=c=0时，函数y=f（x）的图像关于原点（0，0）中心对称）。

四、两个函数图像关于点成中心对称

结论4：设a，b，c均为常数，则函数y1=f（a+x）与y2=c-f（b-x）关于点（—，—）成中心对称图形。

证明：

方法一：已知y1，求出y1关于点（—，—）对称的函数y3，若y3=y2，则证明完毕。

在函数y3上任取一点P（x0，y0），即y0=f（a+x0），则点P关于点（—，—）的对称点为Q（b-a-x0，c-y0），则点Q必在函数y1的图像上。

∴c-y0=f（b-a-x0）=f（b-x0），

∴y0=c-f（b-x），即点（x0，y0）在y2=c-f（b-x）的图像上。

∴函数y3=y2，命题得证。

方法二：函数y1=f（a+x）的图像可以看成是函数y=f（x）的图像向左平移a个单位所得，现在函数y=f（x）图像上任取一点P（x1，y1），则点P1（x1-a，y1）在函数y1=f（a+x）的图像上；函数y2=c-f（b-x）的图像可以看成是函数y=f（x）的图像先关于y轴对称得y=f（-x）的图像，再向右平移b个单位得y=f（-（x-b）），再将所得函数图像关于x轴对称得y=-f（b-x），最后将所得图像向上平移c个单位，即得函数y2=c-f（b-x）的图像，根据函数图像变换可知，点P（x1，y1）经过y2=c-f（b-x）的相应变换得点P2（b-x1，c-y1），又因为点P1（x1-a，y1）和点P2（b-x1，c-y1）关于点（—，—）对称，由于点P（x1，y1）是任取的，所以两函数图像关于关于点（—，—）对称。命题得证。

下面用手持计算器直观呈现（改变a，b的值）。

我们在结论2的基础上探索结论4，我们已经知道函数y1=f（a+x）的图像可以看成是函数y=f（x）的图像向左平移a个单位所得。我们探索一下y2=c-f（b-x）的函数图像的性质。

（1）我们做出函数y=x的图像，再做出y=-x和y=6-x的函数图像。选择命令→绘图→函数（如图19）。

函数图像（如图20）：

我们可以发现y=6-x相当于函数y=x沿y轴对称再上移6个单位。

（2）我们作出原函数y=x2的图像。创建a、b值，作出y=（a+x）2和y= （b-x）2的图像（如图21）。

函数图像（如图22）：

两函数图像关于x=—对称。

（3）创建c值，plot视图，选择命令→绘图→滑动条，最小值到最大值任取，步长为1。作出函数y=c-（b-x）2的图像（如图23）。

隐藏原函数和函数y=（b-x）2。选择函数图像，选择选项→隐藏（如图24）。

（4）在y=（a+x）2作上面的点，选择命令→点→上面的点。做出点（—，—），再上面的点关于点（—，—）的对称点（如图25）。选择命令→变换→反射。

（5）检验点H在否在函数上，现在命令→检验→对象上（如图26）。

移动函数上的点，检验结果为1，证明结论正确。

（6）我们可以改变函数检验结论是否正确，将函数改为x3（如图27）。

结论正确。

参考文献：

[1]陈顺保.两个函数的图像关于直线x=a的对称问题[J].数学教学研究， 1995（4）.

[2]林米尔.关于现代教育技术在数学教育中的应用探索——由图形计算器解数学高考题引起的若干思考[J].现代教育技术，2006（2）.

[3]邱洪文.函数对称性与周期性[J].中学生数学，2015（5）.

[4]赵 媛，张 鹏.图形计算器“颠覆”传统数学课堂[J].中国现代教育装备，2014（12）.

[5]张翠林.浅谈如何通过使用图形计算器初步培养初中生的创新能力[J].才智，2016（15）.

[6]吴绍兵，于 明，赵丽宏.图形计算器在数学概念精加工过程中的作用[J].中国电化教育，2011（11）.

[7]杨大伟，李声持.图形计算器在高中数学教学中的应用[J].中国现代教育装备，2014（12）.

[8]马玉涛.引入图形计算器，改变学生的数学学习思维方式[J].南昌教育学院学报，2013（5）.

[9]何 韬.用科学发展观看图形计算器在高中数学新课改中的使用[J].電子测试，2013（14）.

[10]林 风.基于图形计算器开展数学实验的实践与思考[J].中国电化教育，2012（2）.

[11]张科立.利用图形计算器 有效促进数学理解[J].课程教学研究，2012（11）.

[12]周小蕴，林 威.图形计算器改进学生数学学习的实践与思考[J].中国电化教育，2010（6）.

[13]胡耀华，房爱莲.对图形计算器与数学课程整合的研究[J].中国电化教育，2008（5）.