外1-平面图的均匀点荫度
刘维婵,张 欣
西安电子科技大学 数学与统计学院,西安 710071
1 引言
图论是一门古老的数学分支,它起源于1736年欧拉对于哥尼斯堡七桥问题的研究。近年来,图论学科的发展非常迅速且应用广泛,已渗透到诸如语言学、物理学、化学、电讯工程、计算机科学以及数学的其他分支中,特别在计算机科学中,图论在如形式语言、数据结构、分布式系统、操作系统等方面均扮演着重要的角色。
本文仅考虑简单的有限无向图。设G是一个图,用∆(G),δ(G),V(G)与E(G)分别表示图G的最大度,最小度,点集合与边集合,用|G|与‖G ‖分别表示图G的顶点数与边数。
本文主要研究图的均匀树染色问题。所谓图的均匀树k-染色是一个从图的点集合到数集{1,2,…,k}的映射 c,其满足对于任何 1≤i≤j≤k,都有 |c-1(i)-c-1(j)|≤1,并且由点集c-1(i)导出的子图为一个森林。使得图G具有均匀树k-染色的最小整数k称为图G的均匀点荫度,记为va=(G)。例如,完全二部图K9,9具有一个均匀树2-染色(每一个部染一种颜色即可),而不具有均匀树1-染色,从而va=( )K9,9=2。然而,容易验证完全二部图K9,9不具有均匀树3-染色(如图1的第一张图所示),从而在研究图的均匀树染色的过程中,还需要定义一个染色参数,即图的均匀点荫度阀值。所谓图G的均匀点荫度阀值va*=(G)是一个尽可能小的整数k,其使得对于任何一个不小于k的整数t,图G都具有均匀树t-染色。例如,完全二部图K9,9不具有均匀树3-染色,但是对于每个不小于4的整数k都具有均匀树k-染色(如图1的第二张图所示),从而va*=( )K9,9=4。显而易见,对于任何图G,都有va=(G)≤va*=(G),并且va*=(G)与va=(G) 的差值可以很大。
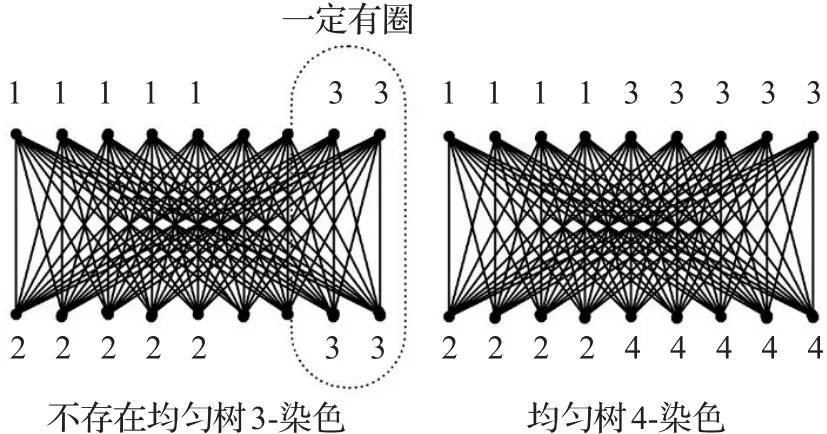
图1 K9,9的均匀树染色
图的均匀点荫度的概念是由Wu,Zhang与Li[1]于2013年提出的,他们证明了va*=(G)≤3对于所有的围长至少为5的平面图成立,va*=(G)≤2对于所有的围长至少为6的平面图以及外平面图成立等结论,同时提出了两个猜想。
猜想1对于任何图G,都有va*=(G)≤「(∆ (G )+1)/2」。
猜想2存在常数C,其使得对于任何平面图G都有va*=(G )≤C。
到目前为止,猜想1(均匀点荫度猜想)已被证明对于完全图以及完全二部图Kn,n[1],最大度至少为|G|/2的图[2],最大度至多为3的图[3]与5-退化图[4]成立。猜想2则被Esperet,Lemoine与Maffray[5]于2015年解决,他们证明了va*=(G)≤4对于所有的平面图G成立。由于Chartrand与Kronk[6]证明了平面图的点荫度至多为3,故Esperet,Lemoine与Maffray认为考虑平面图是否具有均匀树3-染色是十分有意义的。
2015年,Zhang[7]证明了va*=(G)≤3对于任何两个长度至多为4的圈都是点不交的平面图以及围长为4且任何两个4-圈不相邻的平面图成立。将该结论与Wu,Zhang与Li所给出的前述关于平面图的均匀点荫度的结论结合起来,本文提出如下猜想:
猜想3对于任何平面图G,都有va*=(G )≤3。
如果一个图G可以画在一个平面上,使得其所有顶点都分布在G的外面上,并且每条边最多被交叉一次,则称图G为外1-平面图。从这个定义容易看出,每个外1-平面图都是平面图。因此,下文将针对外1-平面图证明猜想3,继而对外1-平面图证明猜想1。
2 外1-平面图的结构
关于图的结构问题的研究是图论领域的一个热门研究方向,在该领域有很多结果,并且有一部分被用于图的染色问题的研究,读者可参阅文献[8-15]了解相关细节。
本章将主要讨论外1-平面图的结构,然后在第3章将其用于研究外1-平面图的相关染色问题。
设G是外1-平面图,并且其已经画在平面上,使得其所有的顶点v1,v2,…,v|G|都按照该次序以逆时针顺序分布在G的外面上,并且每条边最多被交叉一次。按如此方式画好的外1-平面图称为外1-平图。记V[vi,vj]={vi,vi+1,…,vj},V(vi,vj)=V[vi,vj]{vi,vj},分别用G[vi,vj],G(vi,vj)表示由点集V[vi,vj],V(vi,vj)导出的子图。如果vivj∈E(G)并且 | j-i|≠1,| G |-1,则称vivj为外1-平图G的一条弦。本章首先证明如下一个结构引理。
引理1设图G是一个2-连通的外1-平面图,则图G含有以下四种结构之一:
(1)边uv,其中d(u)=2,d(v)≤3;
(2)长度为3的圈uvwu,其中d(u)=2;
(3)长度为4的圈uxvyu,其中d(u)=d(v)=2;
(4)长度为4的圈uxvyu,其中d(u)=d(v)=3,uv∈E(G)。
此外,如果图G含有结构(3)或者结构(4),则按如下方式得到的图H依然是外1-平面图:先将点u删除,此时若xy∉E(G),则将x与y用一条新边连接。
证明 不妨假设图G是一个外1-平图,且不含有上述四种结构之一。如果图G不含有交叉弦,则其为外平面图,而众所周知的是每个外平面图必定含有一条边uv,其中d(u)=2,d(v)≤3,从而G 包含结构(1)。
设弦vivj与弦vkvl在图G中交叉,其中1≤i<k<j<l,并且G[vi,vl]仅含有两条交叉弦,即vivj与vkvl。如果 k-i≥3,则G[vi,vk]中必定含有弦,否则根据图G的2-连通性可推出子图G(vi,vk)是一条路。由于|V(vi,vk)|=k-i-1≥2,故在V(vi,vk)中必定含有两个相邻的度数为2的点,因此图G含有结构(1)。另一方面,如果G[vi,vk]中含有弦,则取其中的一条弦vsvt,使得 i≤s<t≤k并且G[vs,vt]只包含一条弦,即vsvt。此时,再次根据图G的2-连通性又可推出t-s=2且 vsvs+1,vs+1vt∈E(G),从而 vsvs+1vtvs是一个长度为3的圈,并且d(vs+1)=2,于是图G含有结构(2)。因此,k-i≤2。同理可证,l-j≤2,j-k≤2。
如果k-i=2,则必定有d(vk-1)=2,vk-1vk∈E(G)。如果d(vk)≤3,则图G 含有结构(1)。如果d(vk)≥4,则必定有 vivk∈E(G)或者 vkvj∈E(G)。此时若vivk∈E(G),则 vivk-1vkvi是一个长度为3的圈,并且d(vk-1)=2。若vkvj∈E(G),则vkvj-1vjvk是一个长度为3的圈,并且d(vj-1)=2。无论何种情况,均可推出图G含有结构(2)。因此,k-i=1。此时如果vivk∉E(G),则点vl是图G的一个割点,此与图的2-连通性矛盾,因此有vivk∈E(G)。
同理可证l-j=1且vjvl∈E(G)。此时若 j-k=2,则 d(vk+1)=2,vkvk+1∈E(G)。如果 d(vk)≤3,则图 G含有结构(1)。如果d(vk)≥4,则vkvk+1vjvk是一个长度为3的圈,从而图G含有结构(2)。因此,j-k=1。此时如果vkvj∉E(G),则vkvlvjvivk是一个长度为4的圈,并且d(vk)=d(vj)=2,于是图G含有结构(3)。如果vkvj∈E(G),则vkvlvjvivk是一个长度为4的圈,并且d(vk)=d(vj)=3,vkvj∈E(G),于是图 G 含有结构(4)。无论上述何种情况,均可验证G-vk+vivl依然是外1-平面图。
3 外1-平面图的染色
本章首先考虑与图的树染色密切相关的无圈点染色。图的无圈点k-染色是图的一个正常的点k-染色,其使得任何两个色类的导出子图是一个森林。使得图G具有无圈点k-染色的最小整数k称为图G的无圈点色数,记为χa(G)。Borodin[8]证明了每个平面图的无圈点色数至多为5,并且这个上界5是紧的。下面考虑外1-平面图的无圈点染色问题。
定理1如果G是外1-平面图,则χa(G)≤4。
证明 假如该结论不成立,则取G为该定理的极小反例,即 χa(G)>4,且对于任何图H,只要 | H|+‖H‖<| G |+‖G ‖ ,则 χa(H)≤4。显然,图 H 是2-连通的。由引理1,图H包含引理所述的四种结构之一。
情况1图H包含边uv,其中d(u)=2,d(v)≤3。
此时,不妨设d(v)=3。记u的另外一个邻点为w,v的另外两个邻点为v1与v2。由图H的极小性可知图 H′=H-u具有一个无圈点4-染色c。如果c(v)≠c(w),则用颜色 c(u)∈{1,2,3,4}/{c(v),c(w)}染点u。如果c(v)=c(w),则用颜色c(u)∈{1,2,3,4}/{c(v),c(v1),c(v2)}染点u。无论上述何种情况均可得到图G的一个无圈点4-染色,矛盾。
情况2图H包含长度为3的圈uvwu,其中d(u)=2。
由图H的极小性可知图H′=H-u具有一个无圈点4-染色c。此时用颜色c(u)∈{1,2,3,4}/{c(v),c(w)}染点u即可得到图G的一个无圈点4-染色,矛盾。
情况3图H包含长度为4的圈uxvyu,其中d(u)=d(v)=2。
由引理1与图H的极小性可知图H′=H-u+xy具有一个无圈点4-染色c。此时用颜色c(u)∈{1,2,3,4}/{c(x),c(y)}染点u即可得到图G的一个无圈点4-染色,矛盾。
情况4图H包含长度为4的圈uxvyu,其中d(u)=d(v)=3,uv∈E(G)。
由引理1与图H的极小性可知图H′=H-u+xy具有一个无圈点4-染色c。此时用颜色c(u)∈{1,2,3,4}/{c(x),c(y),c(v)}染点u即可得到图G的一个无圈点4-染色,矛盾。
综上所述,该定理的极小反例不存在,从而结论成立。
注1由定理1给出的外1-平面图的无圈点色数的上界4是紧的,例如完全图K4是一个外1-平面图,其无圈点色数恰好是4。
定理2如果G是外1-平面图,则va*=(G )≤3。
证明 由于每个平面图的均匀点荫度阀值至多为4[5],故此处仅需证图G具有均匀树3-染色。由定理1,可以用四种颜色对图G进行染色,即将图G的点集合分成四个两两不交的子集V1,V2,V3,V4,使得由任何两个子集导出的子图是森林。不妨假设|V1|≤|G|/4。由于
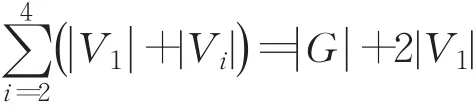
故 必 定存在 i∈{2,3,4},使 得 | V1|+| Vi|≥|G|/3+2|V1|/3。因此,不妨设 |V1|+| V2|≥|G|/3+2|V1|/3,从而 |V2|≥|G|/3-|V1|/3。于是可以取到V2的一个大小为 「|G|/3」-|V1|的子集V,使得S1:=V1∪V的导出子图是森林,并且|S1|=「|G|/3」。
下面考虑集合U2:=V2VU3:=V3,U4:=V4。由于 |U2|+| U3|+| U4|=| G |-| S1|≥2|G|/3,故不妨假设|U2|≤2|G|/9。由于
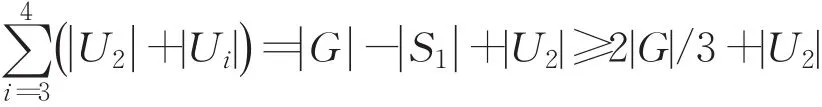
故必定存在i∈{3,4},使得 |U2|+| Ui|≥|G|/3+|U2|/2。因此,不妨设 | U2|+| U3|≥|G|/3+|U2|/2,从而 | U3|≥|G|/3-|U2|/2。于是可以取到U3的一个大小为「|G|/3」-|U2|的子集U,使得S2:=U2∪U的导出子图是森林,并且|S2|=「|G|/3」。
最后,令 S3:=V(G)(S1∪S2),则 S3⊂V3∪V4。从而S3的导出子图是森林,并且 「|G|/3」≤|S3|≤「|G|/3」。
因此,图G具有均匀树3-染色,其三个色类分别为S1,S2,S3。
注2定理2的证明过程说明,只要事先给出了外1-平面图的无圈点4-染色,则必定可以在多项式时间内构造出它的均匀树3-染色。
4 结论
设G是外1-平面图,如果Δ(G)≥4,则由定理2知va*=(G )≤3≤「(∆ ( G)+1)/2」。如果2≤Δ(G)≤3,则由于Zhang在文献[3]中证明了任何最大度至多为3的图都有va*=(G )≤2,故依然有va*=(G)≤「(∆ ( G)+1)/2」。如果Δ(G)≤1,则图G本身就是一个树,从而va*=(G)=1=「(∆ (G )+1)/2」。因此得到:
结论1猜想1对于外1-平面图成立。
另一方面,由于外1-平面图一定是平面图,故由定理2立刻可以推出。
结论2猜想3对于外1-平面图成立。
:
[1]Wu J L,Zhang X,Li H.Equitable vertex arboricity of graphs[J].Discrete Math,2013,313:2696-2701.
[2]Zhang X,Wu J L.A conjecture on equitable vertex arboricity of graphs[J].Filomat,2014,28(1):217-219.
[3]Zhang X.Equitable vertex arboricity of subcubic graphs[J].Discrete Math,2016,339:1724-1726.
[4]Chen G,Gao Y,Shan S,et al.Equitable vertex arboricity of 5-degenerate graphs[J].J Comb Optim,2017,34(2).
[5]Esperet L,Lemoine L,Maffray F.Equitable partition of graphs into induced forests[J].Discrete Math,2015,338(8):1481-1483.
[6]Chartrand G,Kronk H V.The point-arboricity of planar graphs[J].J Lond Math Soc,1969,44:612-616.
[7]Zhang X.Equitable vertex arboricity of planar graphs[J].Discrete Mathematics,2015(1):2696-2701.
[8]Borodin O V.On acyclic coloring of planar graphs[J].Discrete Math,1979,25:211-236.
[9]Zhang X,Drawing complete multipartite graphs on the plane with restrictions on crossings[J].Acta Math Sin:Engl Ser,2014,30(12):2045-2053.
[10]Zhang X.On equitable colorings of sparse graphs[J].Bull Malays Math Sci Soc,2016,39(1):257-268.
[11]张欣,刘桂真,吴建良.1-平面图的结构性质及其在无圈边染色上的应用[J].中国科学:数学,2010,40(10):1025-1032.
[12]张欣,刘桂真,吴建良.不含3-圈的1-平面图的边染色[J].山东大学学报:理学版,2010,45(6):15-17.
[13]张欣,徐兰,刘桂真.稀疏图的k-森林染色[J].山东大学学报:理学版,2011,46(4):1-3.
[14]田京京,聂玉峰,度限制条件下的IC-平面图类中轻弦4-圈的存在性[J].计算机工程与应用,2016,52(20):26-28.
[15]刘维婵,NIC-平面图的轻边存在性及其在定向染色中的应用[J].计算机工程与应用,2018,54(7):62-65.

