基于t分布混合模型的半监督网络流分类方法
董育宁,朱善胜,赵家杰
DONG Yuning,ZHU Shansheng,ZHAO Jiajie
南京邮电大学 通信与信息工程学院,南京 210003
1 引言
近年来,由于网络多媒体业务的不断发展,网络流量的监测管理和网络安全的难度也随之提升。根据Cisco的预测报告[1],到2021年,全球每年的IP网络流量将达到3.3 ZB(ZB;1 000 Exabytes[EB]),将比2016年提高3.2倍;其中视频流量将占所有消费流量的82%。因此,对网络的流量进行分类管理在改善网络环境、保障网络安全等方面具有重要的意义。
网络流分类主要分为四种形式[2]:基于端口、深度包检测、基于统计行为和基于机器学习的方法。然而,由于新型网络应用层出不穷,加密传输、动态端口号等技术的出现使得前两种方法对流分类的准确率大为降低。目前通常采用机器学习的方式进行流分类。
基于机器学习的流分类算法可以分为有监督分类[3]、无监督分类(聚类)[4]和半监督分类[5]。半监督分类是有监督分类和无监督分类的结合。由于其结合了已知标签的样本,可以提前获取部分信息,所以被一些算法所采用。Jun Zhang[6]等人提出了一个半监督的分类模型。该方法使用K-Means和Random Forest算法构建分类模型,并采用流袋进行优化。实验表明该模型可以较好地提高对短时未知应用(zero-day applications)的流分类准确率。Yu Wang[7]等人在考虑了背景信息的情况下,将马氏距离应用于K-Means方法中,提高了分类的准确度。此外,他们将该算法加入对未知聚类的分析,并应用于未知协议的流分类[8]。Shukla[9]等人使用KMedoids方法对KDD CUP 99数据库进行半监督分类的研究。李林林[10]等人针对网络流量分类的类不均衡问题,提出一种K-Means和kNN(k-Nearest Neighbor)相结合的半监督流量分类算法,提高了非均衡流中特别对小类流的识别率。
对于高斯混合模型(Gaussian Mixture Model,GMM)和期望最大化(Expectation Maximization,EM)算法,国内外相关学者也进行了相当多的研究。程华[11]等人根据网络流尺度的Log-normal分布,对数据集进行了GMM建模。Songyin Liu[12]等人将EM算法结合了q-DAEM,降低了传统EM算法的迭代次数。然而,以上EM算法均是基于GMM的。而高斯分布本身对于样本尾部的拟合效果较差,易受到噪声的影响。本文在EM算法基础上,结合t分布混合模型(Student’s t-distribution Mixture Model,TMM)进行改进,并用半监督分类方法验证了算法的有效性。
本文的贡献主要包括以下两点。第一,现有文献中的无监督和半监督的流分类方法通常采用K-Means、EM等算法。但是采用这些算法拟合的模型对数据样本边缘及离群样本比较敏感。因此,本文在流分类时采用t分布代替传统的高斯分布,结合t分布混合模型(TMM)对网络多媒体业务流进行拟合,从而提高了分类的准确率。第二,传统的EM算法执行效率比较低,这是因为如果数据集本身比较复杂,数据样本的边缘信息有可能对每次迭代产生影响,所以收敛速度较慢。本文采用更加复杂的TMM,执行效率将更加低下。为了提高EM的收敛速度,本文使用3σ准则对TMM模型进行限制,提出了有限t分布混合模型(Limited t-distribution Mixture Model,LTMM),降低了EM算法的迭代次数。理论分析和实验结果表明,本文提出的算法模型优于现有文献中的K-Means和高斯混合模型的EM算法。
2 t分布混合模型流分类算法
2.1 高斯混合模型和EM算法
高斯分布(Gaussian distribution)可以较好地描述一般数据样本的分布情况。对于数据集x={x1,x2,…,xN}T,多维高斯分布可由公式(1)表示:

其中,μ表示数据集x的均值;Σ表示数据集x的协方差矩阵;D表示高斯分布的维度。对于网络流分布的数据集而言,每个数据流样本可以通过多种QoS(Quality of Service)特征表示,且每个特征之间还存在一定的相关性。所以为了描述多媒体业务数据集的分布情况,可以引入高斯混合模型(GMM)对样本进行拟合[13],即K个高斯分布的期望:
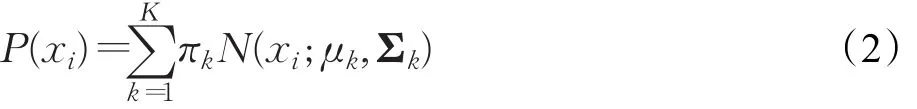
其中,表示第k个高斯分布,该高斯分布的系数用πk表示。需要注意的是,πk应满足公式(3)。

GMM的估计通常采用期望最大化算法(Expectation Maximization,EM)进行迭代拟合。公式(4)~(7)给出了EM算法的迭代公式[7]:
E步:
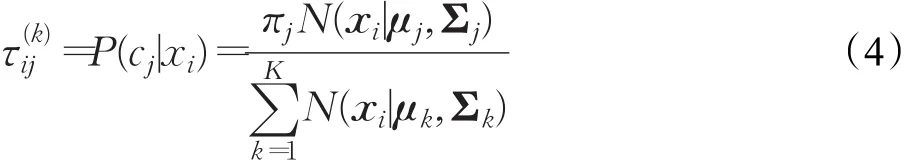
M步:
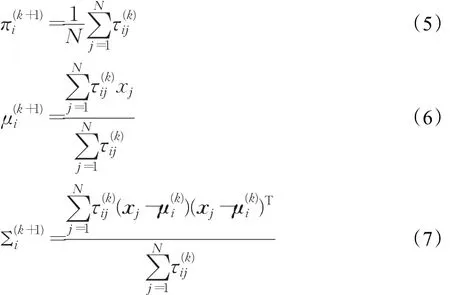
EM算法的收敛条件,即似然函数(公式(8))的变化量小于误差值eps,则表示迭代结束。
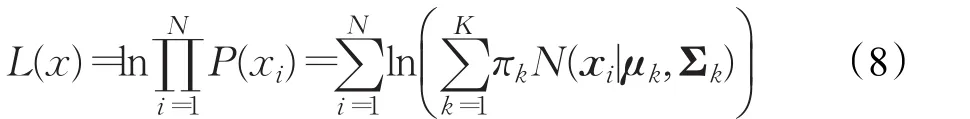
2.2 t分布混合模型和EM算法
上文提到,高斯分布容易受到噪声值的干扰,对数据样本边缘的拟合较差。为了能够更好地拟合数据样本尾部的取值,本文引入了学生t分布(Student’s tdistribution,以下简称为t分布)来代替原有的高斯分布。标准的一维t分布由公式(9)所示:
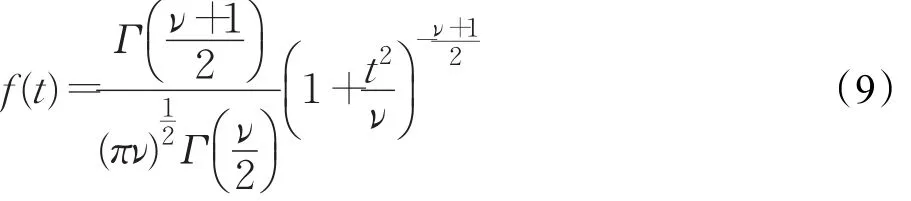
其中,Γ(·)为Gamma函数,ν代表自由度。当ν=1时,t分布退化为柯西分布(Cauchy distribution);当ν=∞时,t分布退化为高斯分布。因此,t分布可以看作高斯分布的拓展。
图1的直方图反映了HTTP网页浏览的平均数据包大小的分布情况。分别用高斯分布和t分布进行拟合。由于使用t分布所具有的“长尾”特性能够更好地匹配数据样本尾部的分布,因此使用t分布模型对数据样本进行拟合,所得到的结果将更准确。
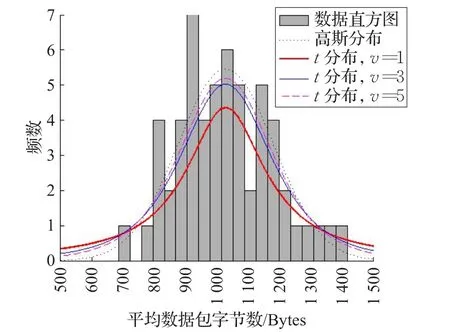
图1 HTTP网页浏览数据包大小的拟合曲线
从物理角度而言,每种多媒体业务流样本的分布是随机且独立的。根据中心极限定理,每种业务可以用高斯分布拟合,而多个业务显然可以构成高斯混合。t分布作为高斯分布的拓展,因此多媒体业务流的数据集使用GMM拓展的t分布混合模型(Student’s t-distribution Mixture Model,TMM)来描述也是相对合理的。常规的多维t分布公式可由式(10)和式(11)给出,TMM的公式可由式(12)表示。
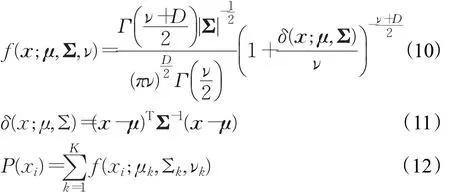
TMM也可以使用EM算法进行拟合。由于TMM还受到自由度ν的影响,根据文献[14],t分布混合模型的EM算法可以修正为:
E步:
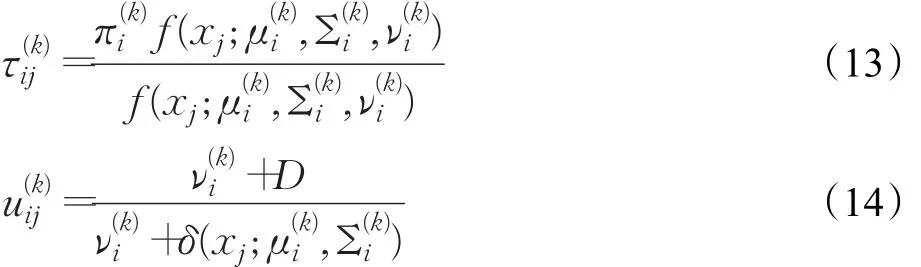
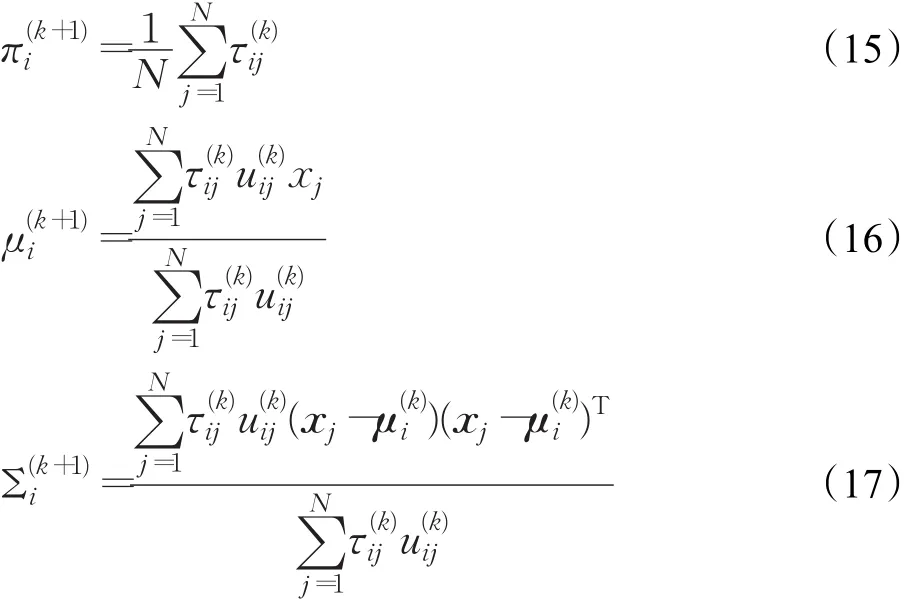
M步:似然函数:
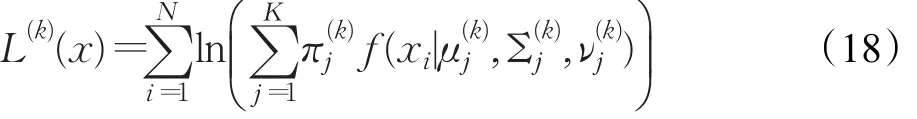
需要注意的是,算法中自由度ν是维度为聚类数K的向量,完整的EM迭代需要不断更新ν的值。为了简化EM算法的计算量,本文取ν为常数,并在实验中用多个ν的取值进行了验证。综上所述,t分布混合模型的EM算法如下所示:
TMM(x1,x2,…,xN,K)
begin
初始化K个中心,记为 μ1,μ2,…,μK
初始化混合模型参数π1,π2,…,πK←1/K
计算每个混合模型协方差Σ1,Σ2,…,ΣK
while true
E步,公式(13)~(14)
M步,公式(15)~(17)
计算似然函数L(x),公式(18)
if|L(k+1)(x)-L(k)(x)|<eps//收敛条件
break
end if
end while
end
3 有限t分布混合模型
3.1 t分布和3σ准则
高斯分布存在3σ准则,即数据样本 X出现在(μ-3σ,μ+3σ)外的取值不足0.3%。换句话说,数据样本在双侧置信度为99.73%的置信区间是(μ-3σ,μ+3σ)。用数学语言可描述为:
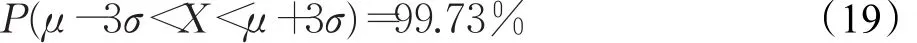
在本文的流分类数据集中,可以用到该结论。我们认为超过这一区间的样本几乎不可能发生,即视为离群样本。为了避免这些离群样本对模型的拟合带来错误的影响,因此可以事先忽略这些离群样本,从而加快算法的收敛。
因为t分布可以看成高斯分布的拓展,所以t分布模型的优化和高斯模型类似。但是由于自由度ν的存在,此时3σ准则已不完全适用于99.73%的置信区间。通过查询t分布表,得到了一个修正的t分布置信区间,如表1所示。
3.2 有限t分布混合模型
传统的EM算法在每一次迭代的时候都要通过第k
步的 μ(k)和 Σ(k)值来更新第k+1步的 μ(k+1)和 Σ(k+1)值。在引入t分布混合模型后,由于模型更加复杂,可能导致计算量上升,迭代次数增加。为了减少迭代次数,本节结合修正的3σ准则,对EM算法的每一次迭代进行了优化,并提出了有限t分布混合模型(Limited t-distributionMixture Model,LTMM)。
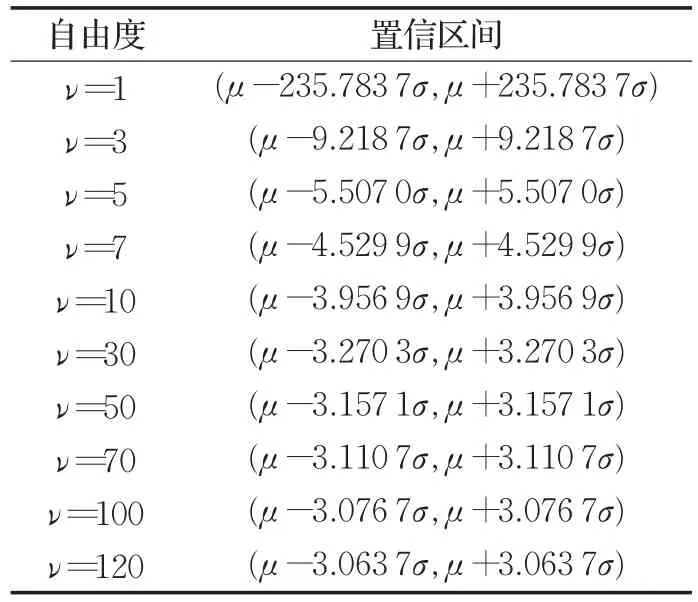
表1 修正的t分布置信区间
根据1.1节,计算高斯混合模型的E步时,需要计算马氏距离的平方(x-μ)TΣ-1(x-μ)。由于马氏距离可以看成是欧式距离‖‖x-μ的拓展[7],所以可以在计算马氏距离时加上限制。这里以ν=5为例,限制条件如公式(20)所示:
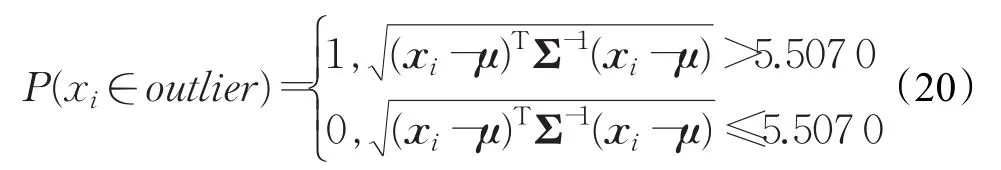
如果某个样本到所有K个t分布的马氏距离均大于5.507 0,那么该样本可以看作是离群样本(outlier)。每一次计算M步的时候,首先忽略掉这些离群样本,那么计算得到μ和Σ就不会受到这些样本的影响。在这一轮迭代结束后,需要把忽略的样本重新加回,保证离群样本不被错误划定。这样就完成了TMM模型的优化。把这种改进的模型称为有限t分布混合模型(LTMM)。同理,高斯混合模型可优化为有限高斯混合模型(LGMM)。
综上所述,有限的t分布混合模型的EM算法如下所示:
LTMM(x1,x2,…,xN,K)
begin
初始化K个中心,记为μ1,μ2,…,μK
初始化混合模型参数π1,π2,…,πK←1/K
计算每个混合模型协方差Σ1,Σ2,…,ΣK
while true
E步,公式(13)~(14),计算离群点,公式(21)
排除离群点,执行M步,公式(15)~(17)
计算似然函数L(x),公式(18)
if|L(k+1)(x)-L(k)(x)|<eps//收敛条件
break
end if
end while
end
3.3 有限t分布混合模型分析
为了更直观地说明迭代过程,这里构建了一个简化的数据分布。图2生成了3个二维高斯分布,其均值和协方差矩阵分别为布均有50个点。那么它们的迭代过程如图2所示。
图2中有限t分布模型中的⊙代表迭代考虑的离群样本。原始数据分布中,存在两个距离数据分布较远的离群样本。迭代结束后,结合TMM的EM算法一共迭代了19次,而LTMM仅迭代了5次。从图2可以看出,虽然开始时迭代效果接近,但当TMM迭代6次之后,其聚类中心的更新都极其微小;而LTMM不受离群样本的干扰,收敛速度很快。这是由于LTMM在每次迭代时能找到更接近迭代中心的μ和Σ值,所以降低了迭代次数,加快了算法的收敛。
4 实验分析
4.1 实验模型建立
本节给出了流分类的实验模型,如图3所示。实验模型可以分为3个部分:数据预处理、聚类过程和分类过程。预处理部分包括:对网络多媒体流进行z-score标准化(即使用标准分数使数据无量纲化[15])、特征选择、划分已标识/未标识样本;聚类过程采用KMeans、SBCK[8]、K-Medoids[9]以及各个混合模型(GMM、TMM、LTMM)进行对比。得到聚类结果可分为三种情况:聚类中没有已标识的样本,则该聚类可视为未知聚类,不在本文考虑范围内;聚类中已标识样本的类型仅有一种,则该聚类中所有的样本均可划分为该类型;第三种是聚类含多种已标识样本的类型。对于这类混合簇,可以进一步对簇中未知样本进行细分类判定,提高分类的准确度[10]。部分文献[6]采用“多数投票”的方式,少部分文献[8,10]进行了细分类工作。由于Random Forest算法不仅分类速度快、分类准确率高,而且相比其他算法可以减少过拟合的情况,所以本文将采用Random Forest作为细分类工作。最后将三种聚类情况综合即可得到半监督流分类模型的分类的准确率。
本文采用半监督方法分类,因而随机选取数据集中的10%作为已标识的样本,剩余的90%作为未标识的样本。为了提高结果的准确性和可靠性,对每个实验均进行10次重复验证取平均值。
4.2 数据集和评价指标
本文数据集采用南京邮电大学校园网内抓取的网络多媒体业务流。数据集的时间跨度是2014年4月到2015年8月,使用的抓包工具是WireShark1http://wiki.wireshark.org/。本文涉及的网络多媒体业务主要可以分为6类,如表2所示。每类业务均为60条数据流,每条数据流的长度均为30分钟。分别选用典型的应用进行实验。
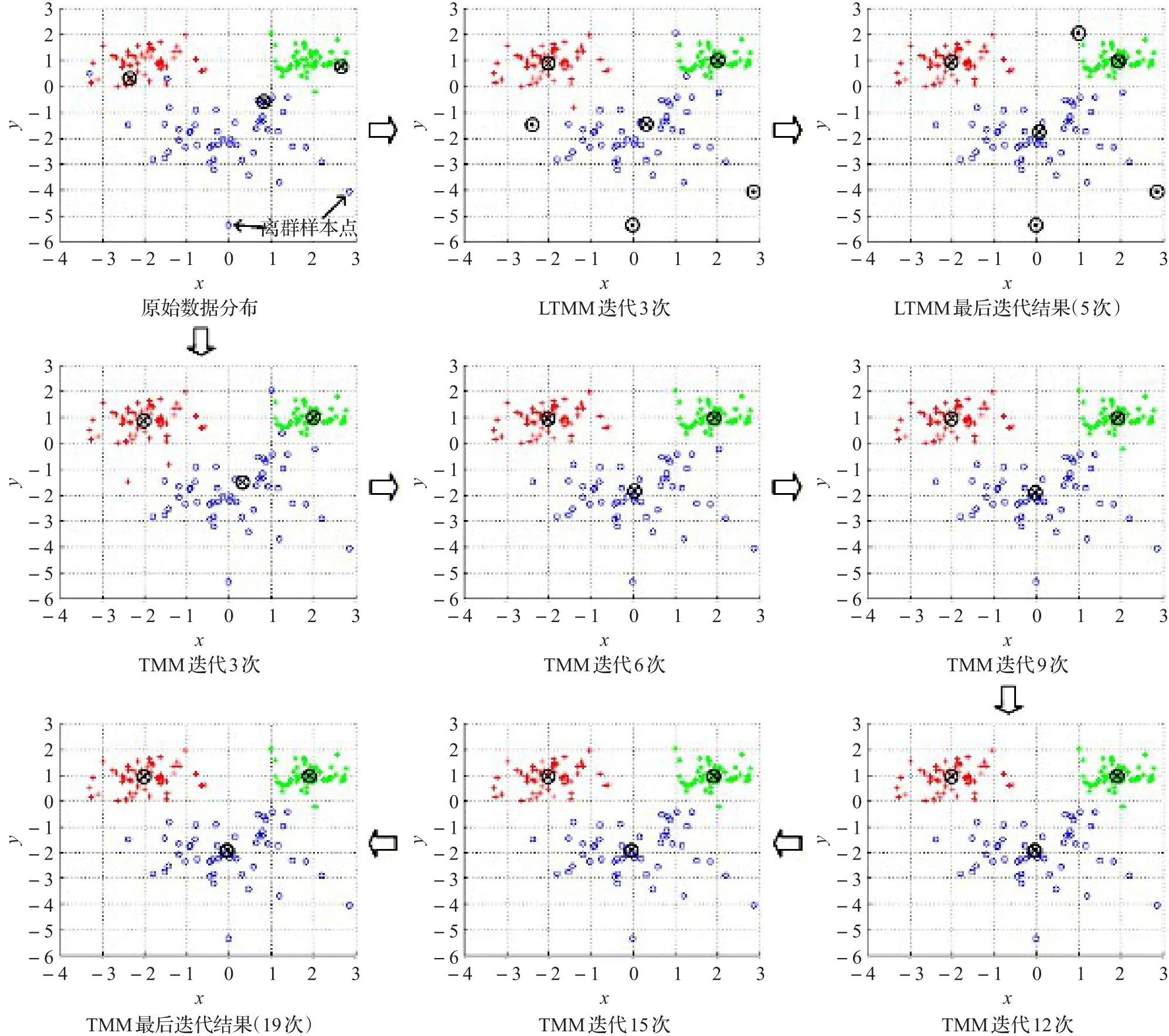
图2 传统t分布模型和有限t分布模型的迭代对比
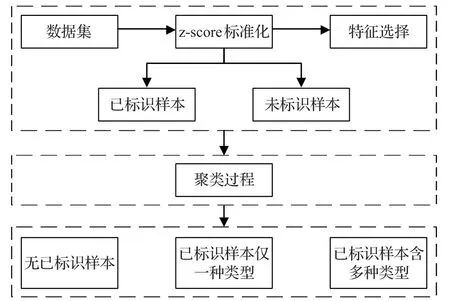
图3 多媒体业务的半监督流分类模型
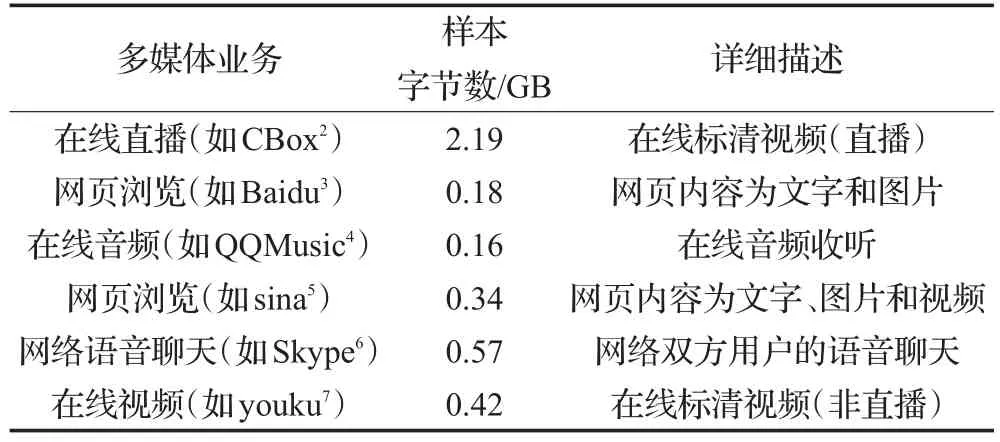
表2 多媒体业务流数据集
衡量网络流的分类结果通常引入四个评价指标:查准率(Precision)、查全率(Recall)、F-测度(F-measure)和总体正确率(Accuracy)。在引入四个指标之前,需要给出二分问题的几种分类结果,如表3所示。

表3 二分类问题的分类结果
其中,TP(True Positive)表示正确样本预测为正确分类的数目;FP(False Positive)表示错误样本被预测为正确分类的数目;FN(False Negative)表示正确样本被预测为错误分类的数目;TN(True Negative)表示错误样本预测为错误分类的数目。进而,四种指标分别由公式(21)~(24)表示:

4.3 特征选择
常用的网络多媒体业务流的QoS统计特征包括数据包大小、数据包传输间隔等。根据数据流传输方向,QoS特征可以分为上行、下行以及整体方向。由于本文针对的网络多媒体流主要集中于下行业务,即下行方向的数据流可以承载更多的特征信息,因此本文主要对下行方向数据流的QoS统计特征进行了相应的研究。
为了能够更加有效地进行流分类,需要找到一个简洁有效的特征组合,以提高分类的准确率,同时降低分类的复杂度。然而,并没有一种最优的特征选择算法能够完全适用于所有数据样本的分类[16]。因此,本文选用了6种常用的特征选择算法,并在本文数据集的基础上进行了特征选择。本文采用信息增益(InfoGain)、信息增益率(GainRatio)或卡方检验(Chi-square)这三种方法选出的特征进行进一步的研究。这些QoS分类特征由表4列出。

表4 实验所采用的特征
不同特征选择算法的总体正确率由图4所示。从图4可以看出,InfoGain、GainRatio和Chi-square这三种方法选出的特征一致,得到的分类正确率较高。此外,虽然一致性特征选择方法(Consistency)对K-Means算法可以获得较高的总体正确率,但在TMM和LTMM算法的总体正确率却不如InfoGain等三种方法选出的特征。
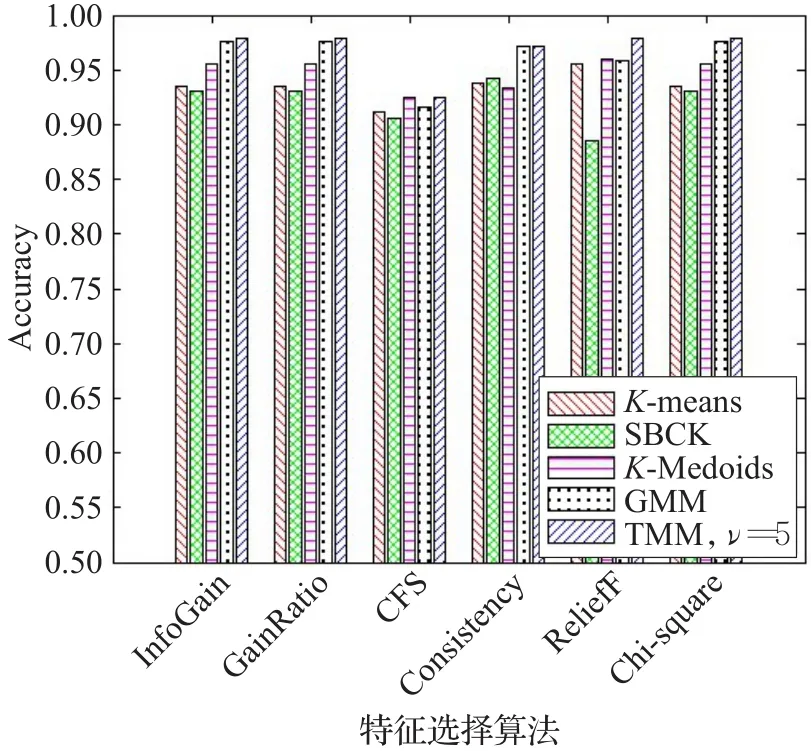
图4 QoS特征选择算法的总体正确率
4.4 自由度的确定
根据3.2节,t分布混合模型根据自由度ν的不同,最后得出的拟合模型也随之不同。因此,为了找到一个比较合适的自由度ν以拟合最后的数据样本,需要对自由度ν进行确定。本节将对提出的TMM和LTMM算法的自由度进行分析。
图5对本文数据集分别执行TMM和LTMM算法,聚类数K取15。从图中可以得出,当ν=3或ν=5的时候,两种模型得到的总体正确率比较高,即更加贴近实际的数据样本。在接下来的实验中,主要采用这两种自由度进行分析。

图5 TMM和LTMM算法的自由度分析
4.5 聚类数的影响
不同的聚类数对K-Means、EM算法均有较大的影响。本节使用半监督流分类模型,探讨不同聚类算法在不同聚类数条件下的影响。
图6给出了不同的聚类数对不同算法的总体正确率。从图6(a)中可以看出,EM算法(GMM和TMM)要优于K-Means部分的算法(K-Means、SBCK和KMedoids)。这是由于K-Means部分的算法通常采用欧氏距离,获得的簇的形状往往是球形的,对非球形簇的聚类并不准确[11]。虽然文[7]中的实验提到他们的算法SBCK要优于GMM,但可能是由于数据集之间的差异,导致本文实验中对SBCK算法的总体正确率较低。对于GMM和TMM而言,本文采用的模型无论取自由度ν=3或5,总体分类正确率均高于GMM模型的分类正确率。因而采用TMM能够更精确地拟合多媒体业务流的数据集。
图6(b)验证了常规混合模型(GMM、TMM)和改进的混合模型(LGMM、LTMM)之间的差异。从图中可以看出,TMM模型的分类正确率均要高于GMM模型的分类正确率,而改进混合模型可能会导致总体分类正确率的降低。这是由于改进混合模型LTMM采用了3σ准则,在每次聚类时可能会过度忽略模型边缘点的影响,因而造成在某些聚类数下的分类正确率的降低。但TMM模型和LTMM模型的拟合结果均优于GMM模型,证明LTMM模型在分类正确率方面还是可以接受的。
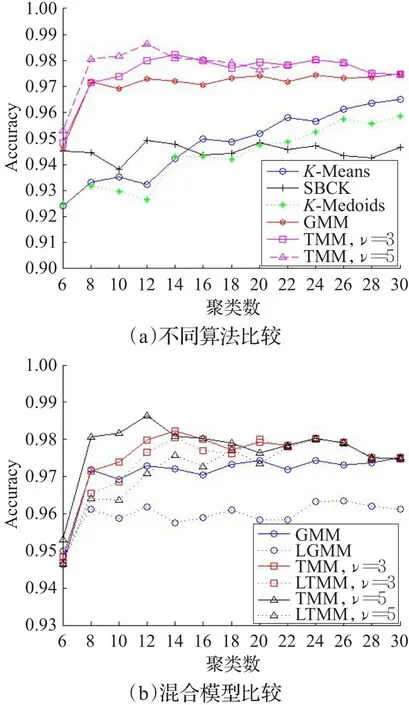
图6 不同聚类数的影响
为了更明显地看出每一类的分类情况,图7列出了各个算法在聚类数为15时的F-measure值。可以看出,本文使用的TMM和LTMM算法确实要优于其他列出的算法。
4.6 迭代次数比对
在本节中,主要对混合模型算法的迭代次数进行实验比较,以验证2.3节的理论分析结果。为简单起见,取聚类数为15,并重复做10次实验取平均值。各算法迭代次数的平均值如表5所示。
从表5中可以得出,使用TMM拟合后,由于算法复杂度增加,因此迭代次数比GMM有所增加。但是有限t分布混合模型(LTMM)的迭代次数小于t分布混合模型(TMM),证明了LTMM可以显著降低算法的迭代次数。虽然LTMM的分类正确率相比TMM有略微的下降,但是由于在迭代次数上降低较明显,所以有限t分布混合模型是可以接受的。
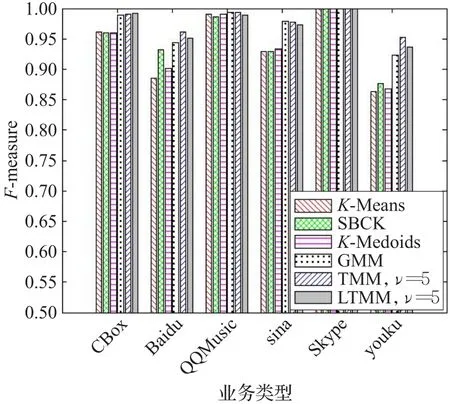
图7 不同算法的F-measure比较

表5 不同算法迭代次数比对
4.7 TMM、LTMM特点及适应场景
由实验可知,TMM、LTMM相较于K-Means和GMM,在准确率、F测度和总体正确率的指标都更优。对t分布自由度v的值进行适当的调整,能够更好地匹配数据样本的尾部分布,提高抗噪声性能,因此t分布拟合的模型可以更好地适用于尾部较长情形。由于引入EM算法,TMM、LTMM拥有EM的优点,能够稳定地处理数据集中的缺损、截尾等不完全数据,但此模型的运算复杂度较高,比较适用于较小型的数据集。从表5可知,与TMM相比,LTMM精确度稍有下降,但高于GMM;然而,其计算复杂度比TMM降低近一半,与GMM相当,所以适用于对计算时间要求较为苛刻的场景。
5 结束语
本文结合t分布混合模型对多媒体业务流进行分类,并用理论和实验证实了t分布混合模型的有效性。相比于高斯混合模型,t分布混合模型对数据集边缘样本的拟合更加精确。为了减少模型中EM算法的迭代次数,本文对t分布模型加以改进,并提出了有限的t分布混合模型,显著地降低了迭代次数。然而,该算法在处理过大的数据集时,可能会导致执行效率低下的问题。在未来的工作中,将进一步优化本文算法,以适用于较大数据集和高维特征的情况。
:
[1]White paper:Cisco VNI forecast and methodology[EB/OL].[2016-2021].http://www.cisco.com/c/en/us/solutions/collateral/service-provider/ip-ngn-ip-next-generation-network/white_paper_c11-481360.html.
[2]Al Khater N,Overill R E.Network traffic classification techniques and challenges[C]//Tenth International Conference on Digital Information Management.IEEE,2015:43-48.[3]Hardt M,Price E,Srebro N.Equality of opportunity in supervised learning[C]//Advances in neural information processing systems,2016:3315-3323.
[4]Li Y,Paluri M,Rehg J M,et al.Unsupervised learning of edges[C]//Computer Vision and Pattern Recognition.IEEE,2016:1619-1627.
[5]Chapelle O,Schölkopf B,Zien A.Semi-supervised learning[C]//Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining.[S.l.]:Springer-Verlag,2009:588-595.
[6]Zhang J,Chen X,Xiang Y,et al.Robust network traffic classification[J].IEEE/ACM Transactions on Networking,2015,23(4):1257-1270.
[7]Wang Y,Xiang Y,Zhang J,et al.Internet traffic classification using constrained clustering[J].IEEE Transactions on Parallel&Distributed Systems,2014,25(11):2932-2943.[8]Wang Y,Chen C,Xiang Y.Unknown pattern extraction forstatisticalnetwork protocolidentification[C]//Local Computer Networks.IEEE,2015:506-509.
[9]Shukla D B,Chandel G S.An approach for classification of network traffic on semi-supervised data using clustering techniques[C]//Nirma University International Conference on Engineering,2013:1-6.
[10]李林林,张效义,张霞,等.基于K均值和k近邻的半监督流量分类算法[J].信息工程大学学报,2015,16(2):234-239.[11]程华,房一泉.基于聚类分析的网络流量高斯混合模型[J].华东理工大学学报:自然科学版,2010,36(2):255-260.
[12]Liu S,Hu J,Hao S,et al.Improved EM method for internet traffic classification[C]//2016 8th International Conference on Knowledge and Smart Technology(KST),Chiangmai,2016:13-17.
[13]Dukkipati A,Ghoshdastidar D,Krishnan J.Mixture modeling with compact support distributions for unsupervised learning[C]//2016 International Joint Conference on Neural Networks(IJCNN),Vancouver,BC,2016:2706-2713.[14]Yao W,Wei Y,Yu C.Robust mixture regression using the t-distribution[J].Computational Statistics&Data Analysis,2014,71(3):116-127.
[15]Han J,Pei J,Kamber M.Data mining:concepts and techniques[M].3rded.SanFrancisco:MorganKaufmann Publishers,2011.
[16]Fahad A,Tari Z,Khalil I,et al.Toward an efficient and scalable feature selection approach for internet traffic classification[J].Computer Networks,2013,57(9):2040-2057.

