软件需求权重的模糊网络分析法
王晓强,王 冬
河南科技大学 机电工程学院,河南 洛阳 471003
1 引言
软件的需求分析在软件的开发过程中起着举足轻重的作用,而需求权重是量化各项顾客需求的相对重要程度,用于指导软件的健壮设计。在软件开发过程中,随着客户对软件的功能要求、性能要求和运行要求等的不断提高,使得顾客需求过于复杂,此时运用层次分析法(Analytic Hierarchy Process,AHP)与模糊层次分析法(Fuzzy Analytical Hierarchy Process,FAHP)求解顾客需求权重就会与真实顾客需求重要度产生较大偏差。因此,为了开发出令顾客满意的软件产品,必须用正确且行之有效的方法对需求权重进行求解和验证。
目前,国内外学者对需求权重的求解进行了相关理论的研究,运用的方法主要包括层次分析法(AHP)、模糊层次分析法(FAHP)、网络分析法(Analytic Network Process,ANP)等。王晓暾等[1]通过融合层次分析法与粗糙集理论提出了粗糙数和粗糙区间两个新概念,用粗糙数和粗糙边界区间来解决顾客需求的含糊性和不确定性。李磊等[2]提出了一种基于模糊层次分析法的多目标决策问题的解决方案,应用基于三角模糊数的模糊层次分析法来求各层次指标权重。周黎莎等[3]将网络层次分析法和模糊综合评价法相结合,对电力企业客户满意度进行综合评价,并进行实例分析,验证该评价模型的有效性和科学性。周晓光等[4]采用模糊优先规划方法确定了各指标的权重,进而通过网络层次分析法计算各指标的综合权重。Yang Shaomei[5]提出了一种改进的模糊层次分析法评估风险的方法,该方法充分利用了三标度法和模糊一致矩阵的优点,更加适合于分析多目标决策问题。Al-Hawari T[6]等将网络层次分析法应用到设施规划上,通过建立网络结构来解决各元素和集群以及它们之间的相互作用,最终确定各方案的优先级别。兰继斌等[7]提出用模糊一致判断矩阵确定方案权重是不完善的,必须考虑参数β的选择,参数β是隐藏在决策过程中决策者的偏好及决策者的分辨能力,同时给出了从传统层次分析法标度到模糊层次分析法标度的转换方法。
AHP与FAHP方法适合于解决系统层次结构中元素的权重问题,但其递阶层次结构限制了它在复杂需求权重决策中的应用;网络分析法适用于需求元素关系比较复杂的权重分析。但网络分析法在判断矩阵求解的一致性和需求元素相对重要度评价的模糊性等方面仍需进一步的深入研究。
本文针对软件开发过程中顾客需求关系较复杂的权重分析问题,运用网络分析法与梯形模糊数相结合的方法,建立加权极限超矩阵,分析需求元素的混合权重,旨在解决各指标层内各元素的相互作用以及指标评价的模糊性所造成权重严重偏差问题,并通过实例验证该方法的可行性。
2 需求权重的模糊网络分析法基本组成
模糊网络分析法是模糊数学与网络分析法相结合的一种方法,主要解决模糊层次分析法和网络分析法中未能解决的问题。梯形模糊数主要解决边界值以及隶属度问题;网络分析法主要建立网络图,解决不同元素组中的元素的相互联系。模糊网络层次分析法为复杂系统中权重的求解提供了依据。
2.1 网络分析法
网络分析法是在层次分析法的基础上,综合考虑各元素组以及组内元素间的相互影响,建立需求元素间的网络结构图,采用超矩阵对需求元素的混合权重进行求解。
ANP结构图(如图1)由控制层与网络层组成[7-8]。控制层中的准则R1,R2,…,Rm相互独立;元素组件(C1,C2,…,CN)构成网络层,其中元素组Cj有元素ej1,ej2,…,ejnj,不同组件中的元素间存在内部依赖和外部依赖,这些依赖就构成了反馈网络,其中箭头所指向的因素影响着箭尾的因素。

图1 ANP结构图
2.2 梯形模糊数及其基本运算
在层次分析法中,通常采用T.L.Saaty建立的1~9标度方法来量化两因素的相对重要度[10]。但在实际中进行两两比较判断时,由于人的主观性以及各个因素的模糊性,各个因素的相对重要度用一个确定的实数来表示存在着不合理性。针对这个问题,一些学者运用模糊区间来界定各因素相对重要度的上下限,本文利用梯形模糊数rij=(a,b,c,d)来定量地表示元素ei比ej的重要程度。通过对各因素进行模糊判断,得到相应的梯形模糊一致互补判断矩阵。
假设M是论域U中的任意一个梯形模糊数,梯形模糊数Fuzzy集对应的隶属函数定义为:

其中 a、b、c、d 是隶属函数的参数,且 a≤b≤c≤d,a与d分别是模糊数的上界和下界,且区间[b,c]是模糊数的中间值,参数a、b、c、d根据模糊网络分析法标度取值。rij可以被四元实数组(a,b,c,d)所确定。
假设梯形模糊数eij=(aij,bij,cij,dij),ekh=(akh,bkh,ckh,dkh),则eij与ekh的代数运算为:
eij⊕ekh=(aij+akh,bij+bkh,cij+ckh,dij+dkh)
eij⊗ekh=(aij×akh,bij×bkh,cij×ckh,dij×dkh)
λ⊗ ekh=(λaij,λbij,λcij,λdij)
其中aij>0,bij>0,cij>0,dij>0,akh>0,bkh>0,ckh>0,dkh>0。
3 需求权重的模糊网络分析法数学模型
3.1 模糊一致互补判断矩阵的改进方法
网络分析法是利用超矩阵求解顾客需求混合权重的一种方法,其求解过程的复杂性使得网络分析法在很多领域中较难得到应用,而判断矩阵的一致性检验是网络分析法中较繁琐的一步验证,研究利用一致性矩阵代替判断矩阵的一致性检验,可以在很大程度上降低求解过程的复杂性。
定理1若模糊互补矩阵R=(rij)n×n满足:∀i,j,k=1,2,…,n,有rij=rik-rjk+0.5,则称模糊互补矩阵R是模糊一致互补判断矩阵[11]。
文献[12]有结论(1)和结论(2):
结论1
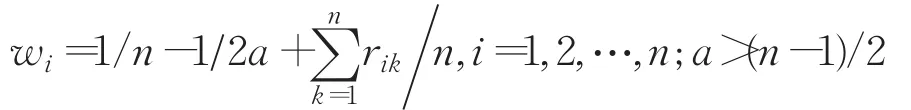
结论2 |wi-wj|≤1/(n-1)
由结论1、2可知,当n较大时,权重之间的偏差会很小,不利于确定各项需求的重要度。
定义1设模糊互补判断矩阵R=(rij)n×n,则R是模糊一致判断矩阵的充要条件存在n维正的归一化向量w=(w1,w2,…,wn)T及 β(β>1),使得 ∀i,j都有 rij=logβwi-logβwj+0.5 成立[7]。
其中权重公式wi为:
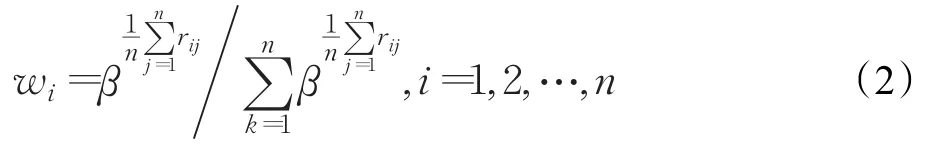
假设 wi(β)>wk(β),则:
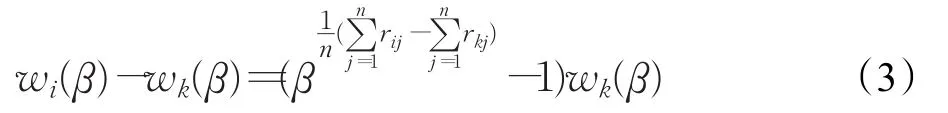
式中
根据公式(3)可知 wi(β)-wk(β)是关于 β 的增函数。故β的变化可以调节权重值的大小,而不会改变各项需求的排序。参数β起着调节权重分辨率的作用。
定义2若A=(aij)n×n是一致的正互反判断矩阵,则R=(rij(β))n×n(β≥81)是模糊一致互补判断矩阵,这里rij(β)=logβaij+0.5(β ≥81)[7]。
通过上述的定义、结论和定理,定理1给出了模糊一致互补判断矩阵,结论1、2说明了定理1在n很大时,权重值并不能反映需求的相对重要度,这样引出模糊一致互补判断矩阵的新定义1、2,其中β值起着调节权重分辨率的作用。
根据定义2,调节β值将1~9标度转换为模糊网络分析法标度,当β=300时,获得表1模糊网络分析法标度。
3.2 模糊网络分析法权重的求解
根据模糊互补一致性矩阵的改进方法,建立改进的模糊互补一致性矩阵R。在Ri控制准则下,以Cj中的元素ejl为次准则,对其他元素组Ci中的元素按其对ejl的影响大小进行间接优势度比较。其中rij为梯形模糊判断向量,设aij为向量rij中的元素,则有0≤aij≤1,aii=1,aij+aji=1,且向量 rij满足 rij=rik-rjk+0.5。rij表示元素ei比元素ej重要的隶属度,rij=(0.5,0.5,0.5,0.5)表示元素ei与元素ej同等重要。

对元素组Ci的模糊一致互补判断矩阵R进行求解,确定元素的排序向量。由于判断矩阵R本身就满足一致性指标,因此可以直接计算eij的综合模糊数Deij:
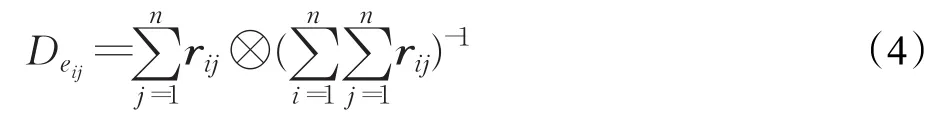
定理2设M=(a1,b1,c1,d1),N=(a2,b2,c2,d2)是两个梯形模糊数,则M≥N的可能性程度为:

其中,a1>0,b1>0,c1>0,d1>0,a2>0,b2>0,c2>0,d2>0。
由公式(5)计算元素eik≥eij的可能性程度,其中 j=1,2,…,ni。确定元素eik大于元素组中其他元素的可能值d(eik)。
d(eik)=minV(Deik≥Dei1,Dei2,…,Dei(k-1),Dei(k+1),…,Deini)(6)式中,k=1,2,…,ni。进而得到元素排序向量(d(ei1),d(ei2),…,d(eini))。归一化得到元素组元素权重向量Wjl。

通过上述求解权重向量的方法,计算在准则层Ri下,以ejl(l=1,2,…,nj)为次准则,计算出超矩阵W的子矩阵Wij。

表1 模糊网络分析法标度

图2 需求结构图
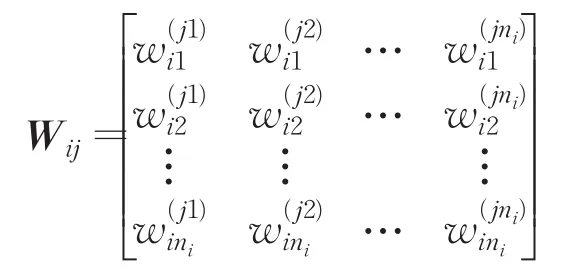
中的列向量就是元素组Ci中的元素ei1,ei2,…,eini对Cj中元素ej1,ej2,…,ejnj的影响程度排序向量。如果元素组之间的元素没有影响,则Wij=0。通过相同的方法最终得到在准则Ri下的超矩阵W。

由于超矩阵W中的子模块Wij的每一列都是归一化的,但超矩阵的整列并不满足归一化要求,因此需要以Ri为主准则,Cj为次准则的条件下,判断网络层中元素组之间的相对重要度。根据上述构建判断矩阵的方法,建立元素组的梯形模糊一致互补判断矩阵。
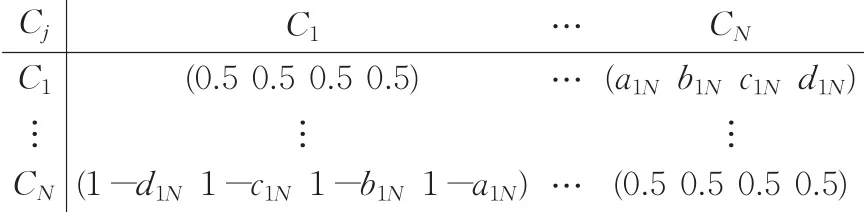
相同的方法得到元素组元素在次准则Cj条件下的权重向量(a1ja2j…aNj),这样的向量有N组,即得到加权矩阵A:

确定加权极限超矩阵,将超矩阵中的子矩阵与元素组的权重做乘积,即:

即为所求加权超矩阵,且每列都满足归一化要求。最后对加权超矩阵进行幂运算,使幂指数趋于无穷,直到每行元素不再发生变化,最终得到加权极限超矩阵。
4 实例应用
在软件开发的过程中,针对顾客需求关系的复杂性,用户需求的模糊性以及软件用户与软件开发人员之间缺乏共同语言等问题,本文以某测量仪软件系统开发为研究对象,采用模糊网络分析法来确定用户对该系统的各项需求权重,并对比模糊层次分析法,以验证该方法的正确性。
在系统的开发过程中,用户对该软件的需求主要包括性能需求、功能需求、界面需求及其他相关需求(如图2)。性能需求主要包括软件的可靠性、可扩展性、安全性、兼容性、系统稳定性和执行效率等;功能需求主要反映在软件必须要实现的功能,而用户对系统要实现的功能主要有数据采集、轮廓/粗糙度/波纹度图形显示、轮廓尺寸标注、粗糙度/波纹度参数评定、运动控制、工作区显示、运动参数设置、指定格式保存文件、打印等;一款好的软件不仅仅局限在强大的功能,软件界面的质量直接关系到用户能否高效、准确、轻松地工作,主要表现在软件的可理解性、易操作性、美观性等;另外还包括其他需求如费用、开发周期等。
4.1 模糊网络分析法
通过分析顾客各项需求之间的相互联系,建立各元素组之间的网络图(如图3)。
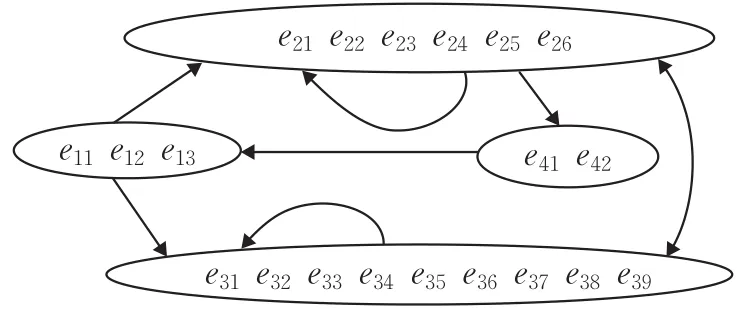
图3 网络层各组件的关联

表2 初始超矩阵
通过对图中各元素组之间元素的相互关联,进行间接优势度比较,即相对于一个准则(主准则),两个元素相对于第三个元素(次准则)的重要度进行比较。图中箭头连线代表元素组之间的元素存在相互制约,以元素组C3中的元素e31为次准则,建立元素组C1的判断矩阵R1。因此需要计算各元素组之间相互影响的优先权重,即元素组优先权矩阵见表3,而这些优先权就是为加权超矩阵对应模块的权重。

将初始超矩阵中的子矩阵分别与元素组的权重做乘积,获得加权超矩阵见表4,其中加权超矩阵的每一列都满足归一化要求。最后通过运用Matlab对加权超矩
由于R1是模糊一致互补判断矩阵,具有满意的一致性,不需进行一致性检验。根据公式(4)解得综合模糊数De1i:

根据公式(5)、(6)求解在元素e31准则下元素组C1的层次单排序。

归一化得e31准则下元素e11、e12和e13权重向量:
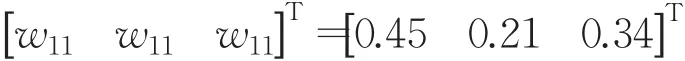
综上,根据网络层各组件关联图得各准则条件下元素组元素的权重向量,建立初始完全超矩阵见表2。
由于初始完全超矩阵的子模块的每一列都是归一化,但是初始超矩阵的每一整列并不满足归一化要求,阵进行幂运算,使幂指数趋于无穷,直到每列元素不再发生变化,此时的矩阵即为加权极限超矩阵见表5。

表3 元素组优先权矩阵
通过表5加权极限超矩阵可知各元素的权重向量为:
(0.031,0.02,0.03,0.097,0.054,0.097,0.061,0.101,0.072,0.058,0.037,0.036,0.042,0.04,0.052,0.058,0.038,0.04,0.022,0.018)
4.2 网络分析法
由文献[8]网络分析法,考虑判断矩阵的一致性检验,根据1~9标度方法,以元素组C3中的元素e31为次准则,建立元素组C1的判断矩阵R1′:
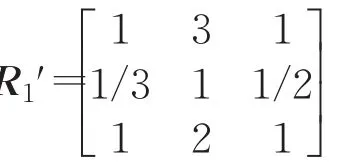

表4 加权超矩阵

表5 加权极限超矩阵
求解判断矩阵R1′,特征向量W′为:
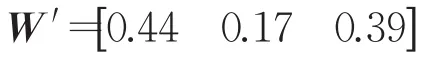
一致性检验有(其中RI=0.58)λmax=3.02,CI=(λmax-n)/(n-1),CR=CI/RI=0.01<0.1 ,即一致性检验符合要求。
相同方法,根据网络层各组件关联图得各准则条件下元素组元素的权重向量,进而获得初始完全超矩阵,最终通过加权极限超矩阵得到各项需求的权重。
(0.027,0.019,0.036,0.090,0.055,0.092,0.061,0.091,0.072,0.060,0.039,0.040,0.043,0.043,0.053,0.057,0.039,0.041,0.022,0.02)
4.3 模糊层次分析法
将文献[13-15]建立的模糊层次分析法模型运用到该测量软件需求权重的求解中,求得界面要求、性能要求、功能要求以及其他要求的元素组内部元素的层次单排序,如下:

然后,对界面要求、性能要求、功能要求、其他要求进行层次排序,如下:

最终确定层次总排序WpiWei,即元素在所在层中的层次单排序值乘以该元素所在层次的权重。得到总排序向量如下:

4.4 方案的比较分析
为选取满意的权重A,通过方案结果的准确性B1、方案的适用范围B2及求解效率B3三方面对模糊网络分析法C1,模糊层次分析法C2和网络分析法C3三种权重方案进行评价。通过定量化比较判断两两之间的相对重要度[10],建立判断矩阵见表6~9。
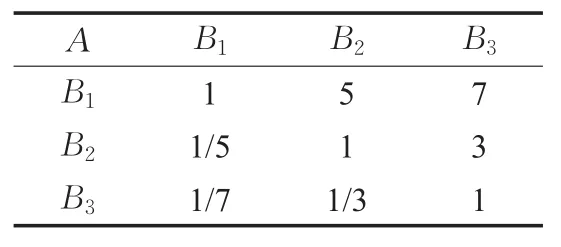
表6 判断矩阵A-B
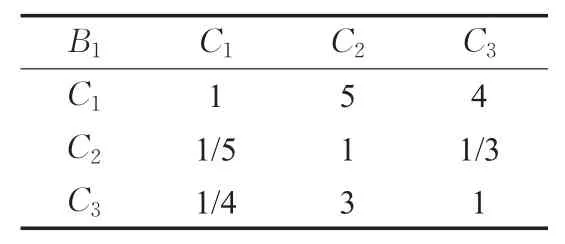
表7 判断矩阵B1-C
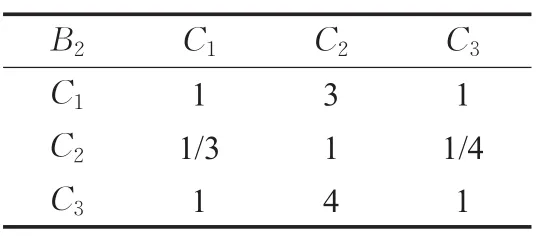
表8 判断矩阵B2-C

表9 判断矩阵B3-C
判断矩阵A-B的特征向量W=[0.73 0.19 0.08]T,最大特征根λmax=3.07,一致性检验有:
CI=(λmax-n)/(n-1)=0.035
则一致性指标CR(其中RI=0.58):
CR=CI/RI=0.06<0.1
判断矩阵具有满意的一致性。
判断矩阵Bi-C的特征向量、一致性指标CR分别为W1=[0.67 0.10 0.23]T,CR=0.069;W2=[0.42 0.13 0.46]T,CR=0.008 ;W3=[0.13 0.69 0.18]T,CR=0.078。则各方案相对于各准则的排序值见图4,层次总排序见图5。

图4 方案各准则排序直方图

图5 各方案总排序直方图
由直方图4~5可知,模糊网络分析法所得权重更能反映顾客的需求强度,更加适合复杂需求关系的权重求解;模糊层次分析法适合求解递阶层次结构中的元素权重,不适合解决复杂关系系统(网络结构)中的权重问题;网络分析法未考虑评价的模糊性评价问题且判断矩阵需一致性检验,使得准确性没有模糊网络分析法高,且求解过程复杂。通过方案的比较分析,由于模糊网络分析法在理论上不但考虑了准则与准则之间、准则与指标之间以及各项指标之间的相互联系,还考虑了模糊性判断和模糊一致互补判断矩阵问题,因此在顾客需求多且复杂的情况时,适合采用模糊网络分析法求解权重。
5 结论
本文着重于在软件开发过程中对顾客需求权重的研究,利用网络分析法和模糊数学相结合的方法,对各项需求建立网络结构,进而利用梯形模糊区间数建立改进的模糊一致互补判断矩阵,整合加权极限超矩阵确定各项需求的权重。
建立的改进一致互补判断矩阵明显提高了判断的一致性和权重的计算效率。利用梯形模糊区间数代替1~9标度方法建立判断矩阵,降低了相对重要度评判的主观性,相对重要度更加准确。
模糊网络分析法与模糊层次分析法实例应用的对比分析表明,模糊网络分析法更适合解决需求过于复杂的系统。
:
[1]王晓暾,熊伟.质量功能展开中顾客需求重要度确定的粗糙层次分析法[J].计算机集成制造系统,2010,16(4):763-771.[2]李磊,王永超,唐雨.基于模糊层次分析法的机械材料选择[J].组合机床与自动化加工技术,2015(11):9-12.
[3]周黎莎,于新华.基于网络层次分析法的电力客户满意度模糊综合评价[J].电网技术,2009,33(17):191-193.
[4]周晓光,高学东.基于FANP模型的建设项目选择方法与应用[J].系统工程理论与实践,2012,32(11):2459-2466.
[5]Yang Shaomei,Liu Jinghua,Wang Rui.The improved fuzzy analytic hierarchy process and its application in risk evaluation of wind power project investment[J].Journal of Information and Computational Science,2014,11(13):4547-4553.
[6]Al-Hawari T,Mumani A,Momani A.Application of the analytic network process to facility layout selection[J].Journal of Manufacturing Systems,2014,33(4):488-497.
[7]兰继斌,徐扬,霍良安.模糊层次法权重研究[J].系统工程理论与实践,2006(9):110-111.
[8]Saaty T L.网络层次分析法原理及其应用[M].鞠彦兵,刘建昌,译.北京:北京理工大学出版社,2015:120-131.
[9]贺纯纯,王应明.网络层次分析法研究述评[J].科技管理研究,2014(3):204-206.
[10]吕永波,胡天军,雷黎.系统工程[M].北京:清华大学出版社,2006:185-199.
[11]张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学,2000,14(2):80-88.
[12]吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2):79-85.
[13]宾光福,李学军.基于模糊层次分析法的设备状态系统量化评价新方法[J].系统工程理论与实践,2010,30(4):744-750.
[14]周艳美,李伟华.改进模糊层次分析法及其对方案的评价[J].计算机工程与应用,2008,44(5):212-215.
[15]李永峰,朱丽萍.基于模糊层次分析法的产品可用性评价方法[J].机械工程学报,2012,48(14):183-191.

