抓住图形变化本质，“变换”视角追根溯源——中考第一轮复习“图形的变换”设计

☉湖北武汉市钢城第二中学 龙金凤

初中阶段“图形变换”主要涉及图形的轴对称、平移、旋转及位似.不同变换下的图形都有各自的性质，这些性质不仅能为合理推理提供依据，同时也是解决许多实际问题的重要工具.图形变换考查学生对基本图形本质的理解，又能培养学生的实践与操作能力，形成空间观念和运动变化的意识［1］，也是中考的热点与难点.在中考复习中，怎样让学生能够将三年学习的知识进行梳理并提升知识板块间的深层次认识，提高学生的复习效率呢？笔者在近期进行了一次第一轮复习的研讨课，谈谈自己的想法及做法，以供大家一起研讨.

一、案例分析

1.课前忆学.

（1）思考：平面内有两个点A、B，如何让点A运动到点B处？

按一定的方法把一个图形变成另一个图形，叫作几何变换.

问题1：初中阶段我们学过哪几类几何变换？

问题2：教材是如何定义的？

问题3：它们有哪些性质？

请同学们完成下表1：

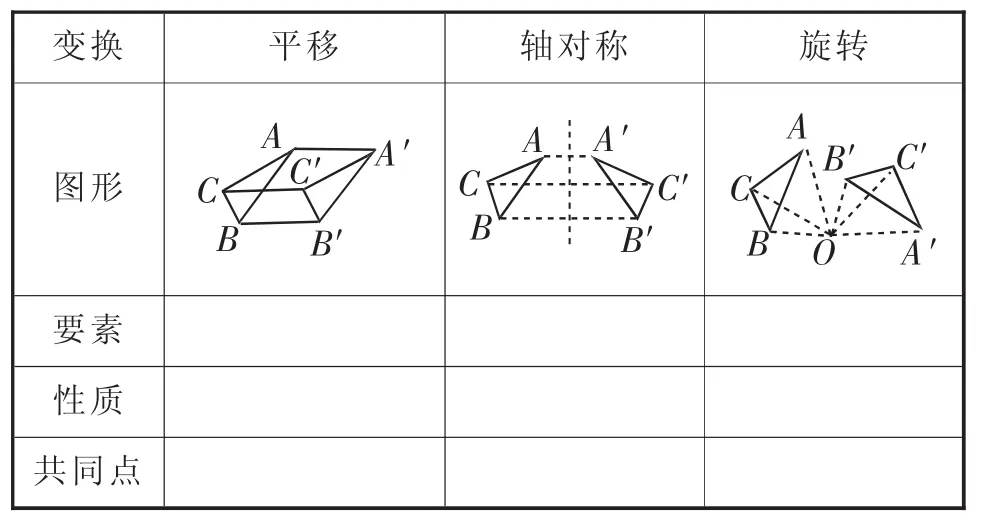
表1

课中追问：

（1）平移的性质梳理时，追问：为什么平移中对应点的连线平行（或共线）且相等呢？

（2）在三种变换共同点的梳理时，引导学生发现它们都是全等变换.追问：有没有不全等的变换？将相似变换补充到知识体系中.

设计意图：（1）通过提出图形变换中最本质的问题——点的运动，让学生回顾复习初中阶段学习的变换.学生能够想到按照平移、轴对称、中心对称及普通的旋转达到运动的效果.为学生梳理这几类变换都是按照一定的方法把一个图形变成另一个图形，也就是几何变换，切入本节课的复习内容.

（2）回归课本，梳理三类变换的概念及性质.引导学生梳理性质时从点、线、面的层面关注变换前后两个图形间的关系.同时在课中追问：为什么平移中对应点的连线平行（或共线）且相等呢？让学生体会对应点的连线平行（或共线）是由于平移的方向一样，对应点的连线相等是由于平移的距离一样.也让学生能够体会几何图形间的关系包括数量关系和位置关系.

2.目标导学.

表2

设计意图：让学生能够明确知道中考要求学生会利用图形的变换作图及利用图形变换的性质进行应用.

3.集中研学.

复习平面图形中最基本的元素——点在平面直角坐标系中的变化规律：

（1）点P（x，y）向右平移a个单位，再向上平移b个单位长度，得到的对应点P1的坐标为_____.

（2）点P（x，y）关于x轴的对称点P2的坐标为____.

点P（x，y）关于y轴的对称点P3的坐标为____.

（3）点P（x，y）关于原点的对称点P4的坐标为____.

设计意图：先从点的变化规律复习，再逐步发展到线（直线、曲线）、面（平面图形）的运动变换.

例1如图1，在直角坐标系中，A（0，4）、C（3，0）.

①画出线段AC关于y轴的对称线段AB.

②将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD.

③写出从线段AB到线段DC的变换过程.

④写出从线段AB到线段CD的变换过程.

课中追问：（1）在第①问完成后，追问学生：AC还可以怎样变换到AB？

（2）在第②问中，追问学生：需要什么作图工具？

（3）从线段AB到线段DC与到线段CD有何不同？

设计意图：（1）本题为武汉市2014年与2015年中考题目的融合，考查学生的作图能力.其中第一问考查学生的轴对称变换，在追问①中让学生用不同的变换视角看待问题，将静态的平面图形“动态”化，发展学生的空间想象能力.

（2）从线段AB到线段DC的过程可以是平移、也可以是先沿y轴轴对称（或旋转）再沿直线x=3轴对称（或旋转）得到，让学生能够体会到几种运动变换之间的关联.

（3）通过第③和④问的对比，让学生能够再次体会变换前后图形的对应关系.

图1

为曲线C1，将其向左平移2个单位长度，得到曲线C2，请在图中画出C2，并直接写出C1平移至C2处所扫过的面积并思考：能求出C2的解析式吗？

课中追问：除了将C1平移，我们还可能将C1进行什么样的变换呢？请独立思考，设计一种与变换相关的题目，课后与同学交流.

设计意图：（1）本题选自2016年武汉市中考，让学生通过中考来感受对图形变换的考查.

（2）由例1直线型的变换过渡到曲线型的变换，让学生体会运动变换的本质是点的变换.

（3）让学生自己想象C1的运动变换，激发学生的空间想象能力，思考C2的解析式的求法，发展学生的推理能力.

图2

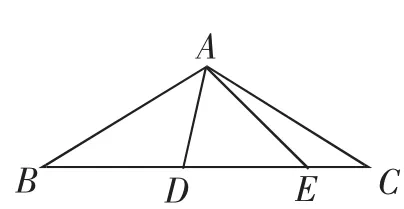
图3

解法1：解法2：

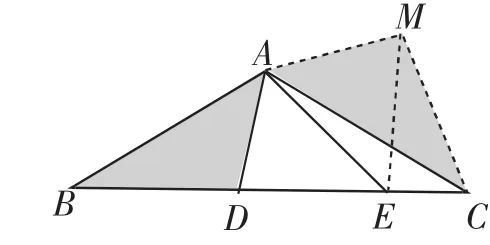
图4

图5

课中追问：

（1）线段AB和AC有什么关系？

（2）∠BAD与∠CAE有什么关系？

（3）我们如何将BD、CE以及相关信息合理利用呢？

设计意图：（1）本题选自2017年武汉市中考，为学生提供最直接的中考考题方式.

（2）利用有公共端点的相等线段的信息，以及∠BAD+∠CAE＝60°这两方面把关于线段和角的信息整合，引导学生用变换的角度思考问题.

（3）利用“合”的想法产生解法1，利用“分”的想法产生解法2，与证线段和与差中的“截长补短”的思想方法的内核相通.让学生能够体会运动变换后可以将图形中的线段及角这些分散的信息集中.

练习2：如图6，在矩形ABCD中，点E、F分别在边BC、CD上，且∠EAF＝∠CEF＝45°，若DF＝3，EF＝，则AD的长为________.

解法1：

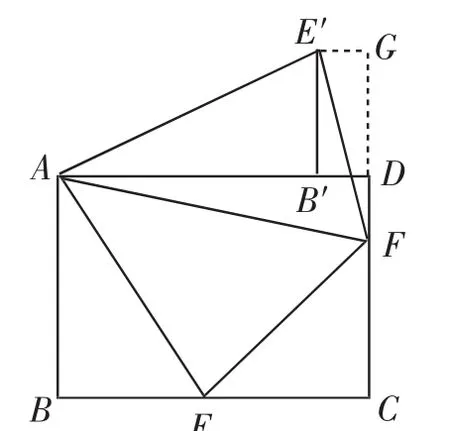
图7

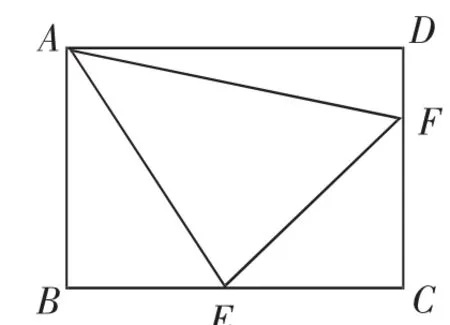
图6

解法2：（化归为例2）

图8

解法3：（相似）

图9

课中追问：（1）目前可以挖掘一些什么信息？和例2比起来有什么区别呢？是否还是可以借助例2的想法呢？

（2）此题和例2的区别在于载体变成了四边形，45°的角在∠DAB中，但∠DAB所在的不是三角形，你能够化归成与例2类似的情况吗？

设计意图：（1）发展学生的思维能力，让学生活学活用，不拘泥于之前老师总结的解题规律，引导学生遇到新题目如何思考问题.

（2）引导学生抓住核心要素，思考需要集中的信息有哪些？我们如何进行集中？遇到新题目的呈现，我们如何化归为已学过的知识.

二、课后思考

1.抓住本质，寻找知识的生长点.

第一轮复习起到了知识梳理与整合的作用，应以学生为知识梳理的主体，让他们自主经历题组解答和互动交流的过程，推动基础知识的有效入网［2］.本节课着手于图形的运动变化，以点、线、面的方式铺开，用运动变化的观点思考问题，让学生体会学习运动变换的作用，为学生的中考复习备考提供有力支撑.

2.培养学生能力，让学生学会如何思考.

在平时的教学中，教师常给学生总结各种几何基本图形的方法，学生机械化记忆或者训练能够让学生形成条件反射，可是为什么我们要这样作辅助线呢？学生可能并没有理解.基于对知识本身的追溯，引导学生如何思考应成为教师教学中的着力点，引导学生通过观察、联想，形成自己的认知经验.

如果教师能够帮助学生在中考备考中梳理好知识脉络，形成知识体系，打通各个知识板块中的关联，做到心中有教材，心中有学生，多引导学生思考问题的本源，可以提高学生在数学课堂中的成就感，实现有效中考复习备考，为考生助一臂之力.

参考文献：

1.黄云兴.图形变换问题在中考中的应用探究［J］.新课程学习（上），2014（7）.

2.孙来扣.中考复习，从“起点”再出发——以“一次方程（组）”复习为例［J］.中学数学（下），2015（6）.