基于时间序列数据挖掘的地铁车门亚健康状态识别方法
薛 钰,梅 雪,支有冉,许志兴,史 翔
(1.南京工业大学 电气工程与控制科学学院,南京 211816; 2.南京康尼机电股份有限公司,南京 210013)
近年来,城市人口的急剧增加,城市规模的增大,致使城市的交通系统面临严峻的局势。地铁作为公共交通中重要的组成部分,是目前人们主要出行方式之一。列车车门由于其工作环境中经常受到挤压和震动,所以它是整个车辆中故障频发的部分[1]。车门打开和关闭过程中最重要的驱动部件就是电机,其工作状态可以直接或间接反映出车门的工作状态。最近这些年人们提出多种方法用于电机的故障诊断,例如基于神经网络的方法[2]、基于信号处理的方法[3]和基于规则发现的诊断方法[4]等。车门亚健康状态不同于故障,是介于车门正常运行和故障之间的中间状态,对其进行识别存在重要意义。
由于车门电机参数为时间序列相关的数据,故可以利用时间序列数据挖掘算法和技术来对电机的运行状态进行分析。目前,时间序列常用的表示方法有离散小波变换、分段线性表示和符号化方法。文献[5]采用离散小波变换处理地震波时间序列,将转化后小波的系数作为特征,实现对地震信号的跟踪。文献[6]等依据时间序列中斜率的变化,提出了基于一阶滤波的时间序列分段线性表示方法(Piecewise Linear Representation method of time Series based on First-order Filtering, PLR_SFWF),将时间序列分段线性表示。文献[7]挖掘字符串处理后时间序列中的频繁模式,实现时间序列的聚类以及分类。虽然上述的算法对时间序列处理效果很好,但遗憾的是运算比较复杂,难以应用于地铁车门电机数据处理中。本文针对地铁门电机数据提出了一种新的亚健康识别算法。首先,采用多尺度滑动窗口的方法并结合拓展符号聚集近似(Extension of Symbolic Aggregate approXimation, ESAX)算法对地铁门电机数据进行挖掘;然后,采用主成分分析(Principal Component Analysis, PCA)法降维并选择较为敏感的参数作为亚健康判断的特征量;最后,结合基础特征利用分层模式识别模型对各类亚健康状态进行识别,并以实测地铁门电机数据为例验证本文所提方法的有效性。
1 地铁门电机数据特征提取
1.1 时间序列符号化
Lin等[8]提出符号化聚合近似(Symbolic Aggregate approXimation, SAX)算法,对于长度为n的时间序列X,若要将其用长度为w的字符串表示,需要进行下面四个步骤:
1)对数据X进行标准化处理。对于标准化后的时间序列,数据往往呈现高斯分布,计算公式如下:
(1)
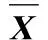
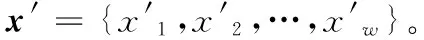
3) 依据间断点β={β1,β2,…,βα-1}将高斯空间等概率划分,其中的区间个数为α。间断点可以查表获得,表1给出了α从3到5时的间断点的值。

表1 高斯空间等概率划分断点(α为区间个数, β为断点)Tab. 1 Breakpoints that divide a Gaussian distribution into equiprobable regions (α is the number of regions, β are the breakpoints)
1.2 改进时间序列符号化
SAX在应用中的良好效果使其成为近10年来被广泛使用的一种符号化特征表示方法;然而,只计算均值往往会忽略时间序列中的极值点。图1为车门在刚启动阶段时的电流曲线,通过SAX算法可以将其离散化为字符串DCBCDE(a=6,w=6)。可以发现,图1中很多重要的极值点信息被忽略了,这些极值点记录车门运行过程中一些极端且不寻常的模式,这些模式往往是进行识别的关键。文献[9]提出了拓展符号聚集近似(ESAX)算法并将其应用于金融数据处理,其思想是在计算均值的时候同时引入最大值和最小值,以此来保留时间序列数据中的极值点。
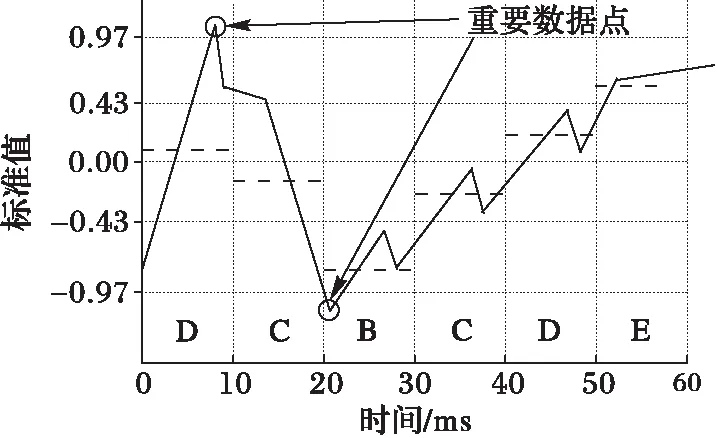
图1 通过SAX字符化车门电机电流曲线 Fig. 1 Current data of motor represented by SAX
图2为使用ESAX算法对电流曲线进行离散化。当α=6,w=6时,曲线离散字符化结果为BDFECBABBBCCCDDDEE。这种改进的字符化算法能够保留图中的极值点信息,缺点是使得原来长度为6的字符串变为长度为18的字符串。
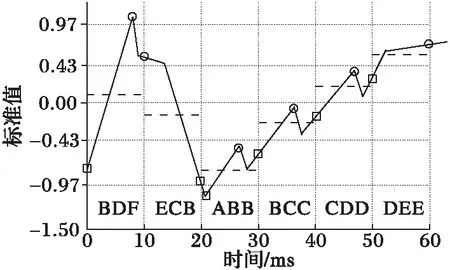
图2 通过ESAX字符化车门电机电流曲线 Fig. 2 Current curve of motor represented by ESAX
为了使ESAX算法进一步适用于车门电机数据,对其作出改进,结合滑动窗口重叠分割法来离散时间序列[10]。滑动窗口的原理如图3所示,其将时间序列分成若干等宽的短序列,序列个数为N-s+1(为了避免序列末端数据剩余,取步长r=1)。

图3 滑动窗原理 Fig. 3 Principle diagram of sliding window
1.3 基于多尺度滑动窗口的特征提取
地铁车门所受的阻力主要来源于机械阻力、空气阻力、密封条反弹力和密封条摩擦力四个方面,而这些阻力受到温度和湿度等环境的影响。车门在开关门过程中的开始阶段和结束阶段阻力变化较大,从而使得这部分电机的转速和转矩信号变化明显。图4为车门开关门时电机的转矩曲线,依据曲线的变化,将开关门过程大致分为3个阶段,即启动段、匀速段和减速段。开关门过程中启动段和减速段蕴含着更多的车门状态信息,对这两个阶段的数据挖掘有着更加重要的意义。在本文中,采用一种多尺度的滑动窗口的方法对开关门过程中的转速、转角和电流信号进行挖掘,在匀速阶段采用较大的滑动窗口来将时间序列离散成字符,在启动段和减速段采用比较小的滑动窗口进行离散。在尽可能多地挖掘时间序列数据特征的同时降低数据的维数。
通过符号化特征表示之后,可以识别车门电机参数形态特征,接着通过选取合适的距离度量的函数,可以找出数据之间的差别。欧氏距离[11]和最小距离[8]是目前最常见的两种计算离散字符序列距离的方法。本文通过对最小距离方法的改进,计算时间序列的相似性。对于字符化后的时间序列AEsax={a1,a2,…,an}和BEsax={b1,b2,…,bn},计算公式如下:
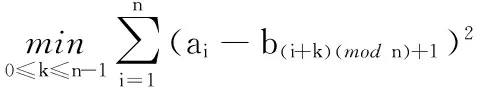
(2)
其中:c为压缩率,c=3n/w,n为滑动窗口长度,w为字符化后字符的个数;ai和bi来自字符表V={V1,V2,…,Vn},且
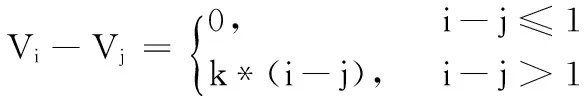
(3)
其中k为间断点β={β1,β2,…,βn}之间的距离。
本文基于多尺度滑动窗口的符号化特征提取算法如下:
1) 初始化相关数据。字符种类数α=6,字符个数w=5,电机的转角数据滑动窗口长度s=120;转速和电流数据在启动段和减速段滑动窗口长度s=30,匀速段滑动窗口长度s=120。
2)标准化车门正常状态下的模板曲线,利用滑动窗口对其中的转角、转速和电流曲线依次分段,并通过对子序列均值、最大值和最小值的计算,将时间序列离散成ESAX字符串。
3)对亚健康和其对应正常数据的电机转速、转角和转矩曲线预处理,包括问题数据的去除和数据长度的处理,然后采用步骤2)的方法进行离散,获得离散后的字符串序列。
4)利用式(2)分别计算亚健康状态下转速、转角和转矩和模板之间的距离,即d(ESAX,ESAXT),将其组合获得距离表示的特征集。
步骤2)中模板曲线对车门亚健康状态的识别有着重要意义。由于地铁门受其工作环境和人为因素的影响,使得其正常状态之间的曲线也存在差异,比如温度的降低或者气压的增加,车门开关过程中受到的阻力会变大,其电机电流将会增加。因此有必要考虑各亚健康对应的模板曲线,以减小实验过程中门的调整所带来的误差,提高特征的可靠性。本文将车门调整之后正常运行一段时间数据的均值作为模板曲线。
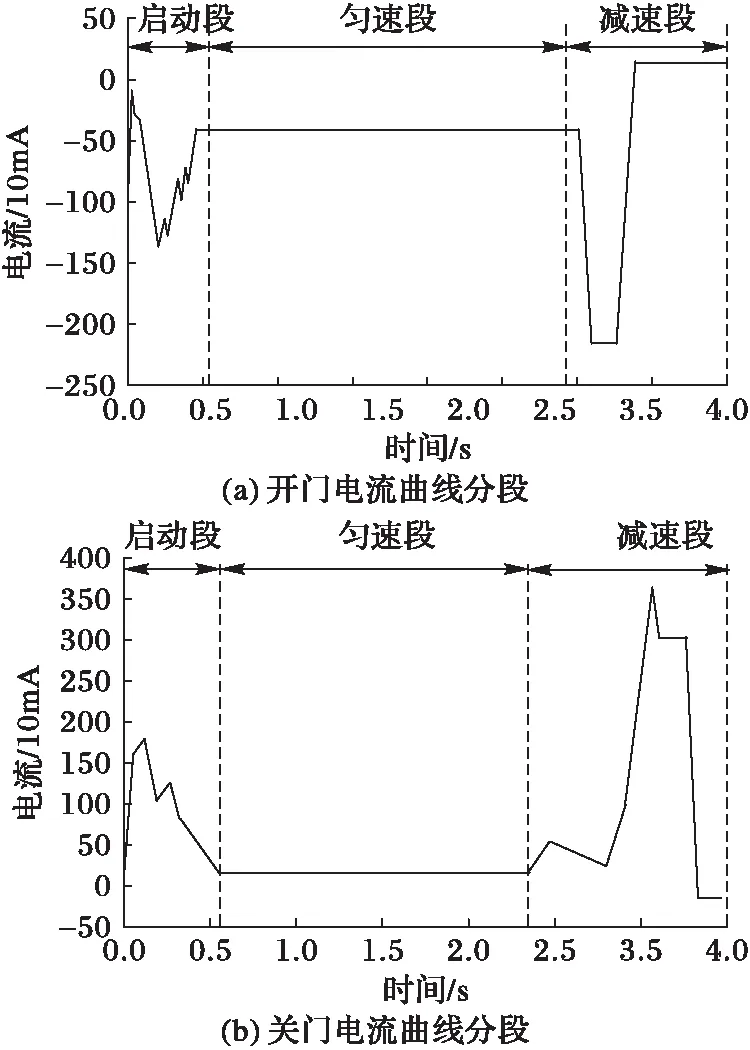
图4 电机电流曲线分段 Fig. 4 Curve segmentation of motor current
2 分层亚健康状态识别模型
在实际的地铁车门亚健康状态诊断中,亚健康类别与亚健康的状态并不存在完全的一一对应的关系,部分亚健康例如电机组松动、下挡销干涉对电机的运行过程中所造成的阻力干扰比较小,对曲线的变化不如其他亚健康状态明显。将这些靠近正常状态的亚健康状态归为Ⅱ类亚健康,而将远离正常状态的亚健康归为Ⅰ类亚健康。本文采用一种由粗到精细分层分类的算法[12],对2类亚健康逐层进行区分,算法流程如图5所示。
分层亚健康状态识别算法含有2层识别过程:针对正常数据和亚健康数据,首先采用字符化处理对数据进行挖掘,获得距离表示的特征集,接着使用主成分分析(Principal Component Analysis, PCA)进行降维,去除冗余信息并选择贡献率较高的特征用于第一层分类;第一层的训练识别的过程主要针对Ⅰ类亚健康,这类亚健康往往拥有着很高的区分度。在第二层识别中,通过融合数据的基础特征和距离表示的特征集,进一步区分出Ⅱ类亚健康数据和正常数据。本文的分层亚健康识别模型采用鉴别能力和推广特性较好的支持向量机(Support Vector Machine, SVM)作为分类器。
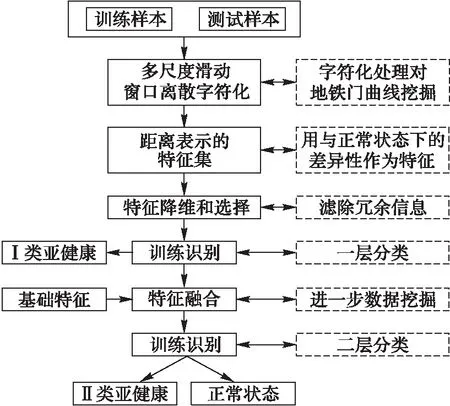
图5 分层亚健康识别模型 Fig. 5 Hierarchical sub-health state identification model
SVM的本质是采用核函数将特征非线性映射到高维空间,并在高维空间寻找最大间隔分类面。SVM常见的核函数包括线性核、高斯核和Sigmoid核,本文选用高斯核。SVM在进行分类时通常会引入松弛变量ξ和惩罚系数C,求解软边界二次规划问题。其中C>0为一个自定义的惩罚因子,它决定对错分样本的惩罚程度,用来控制样本偏差与机器泛化能力之间的平衡。C越大,惩罚就越大,暗示着对离群点的重视程度也越高,其取值与具体应用有关。当各亚健康特征的区分特性较好时,可以适当提高惩罚因子,以提高SVM分类能力。当亚健康特征区分度较差时,必须适当减小惩罚因子,保证分类器有着比较好的泛化性能。因此,在第一层分类模型中选择较大的C来区别出Ⅰ类亚健康;第二层分类模型中,减小C的取值,以得到较为准确的识别结果。
在每一层的分类识别过程中,需要同时对多种亚健康状态进行分类。单个支持向量机只能解决二分类问题,对于多分类问题,本文使用一对一的方法来实现多分类的功能。通过在各个亚健康之间构造决策函数,对t个类别共需构造t(t-1)/2个决策超平面。当对未知亚健康数据进行分类时,采用投票法,即得票最多的类为样本所属的类别。
传统特征[13]通过总结时间序列中一个单一的值来描述时间序列,本文称这些特征为基础特征。这些特征计算简单并且快速,实时性效果比较好,因而在实际中被广泛地使用。常用的基础特征类型包括三种:1)简单的静态值,例如时间序列均值、最大最小值、方差、标准差、斜率;2)频率主导特征,例如时间序列的傅里叶变换以及穿越横轴的次数和频率;3)不同序列之间的相关特征,例如协方差、相关系数、欧氏距离等。本文采用的基础特征主要包括两部分:一是运动曲线静态值特征,通过对三种曲线的分析,启动段提取的特征包括最大转速以及其对应的转角、加速度和最大电流。匀速段提取的特征包括最大转速、平均转速和电流的有效值。减速段提取的特征包括最大加速度、最大电流、截止转速、电流有效值和开关到位堵转电流以及时间。二是曲线与模板曲线的相关特征,包括协方差和相关系数的计算。其中相关系数反映当前曲线与模板曲线的相似程度,协方差反映当前曲线与模板曲线的总体误差。
3 实验结果分析
3.1 数据来源及分析
实验所依赖的地铁门台架为塞拉门结构,通过对其进行调整来模拟各种亚健康状态。数据采集由内置的采集设备对电机开关门过程中的各项数据实时采集,并通过无线传输的方式(由外置监测设备转发)将数据信息传到数据中心服务器。电机数据采集设备(编码器)由采样电路、霍尔传感器及无线传输模块等组成,采集的数据量包括转角、转速和电流,数据采集流程如图6所示。

图6 数据采集流程 Fig. 6 Data acquisition process
主要针对实际运行过程中地铁门可能发生的各种常见亚健康进行分析,通过对门结构进行微调整来模拟这些常见的亚健康状态,本实验包括的亚健康类型主要有V型异常、电机组件松动、对中尺寸变化小、对中尺寸变化大、上滑道外移、下挡销横向干涉、下挡销纵向干涉和压轮过压这8种。由于每次的实验过程中地铁门的调整都会对门的正常状态造成影响,所以每一组亚健康都对应一组正常数据。
在实验中,选取8种亚健康状态下的电机数据,每种亚健康状态选取约40组数据(每组数据又分别包含开门数据和关门数据),每组正常数据也约40组,分别与亚健康数据一一对应。图7为其中的一种亚健康状态(对中尺寸变化小)以及其对应的正常状态曲线。从图7中可以看出,亚健康曲线与正常曲线相似程度比较高,其中转角的正常曲线和亚健康曲线基本重合;转速曲线和电流曲线在匀速段基本重合,在启动段和减速段差异较为明显。其他各组亚健康情况基本类似,所以选取了一组亚健康进行说明。
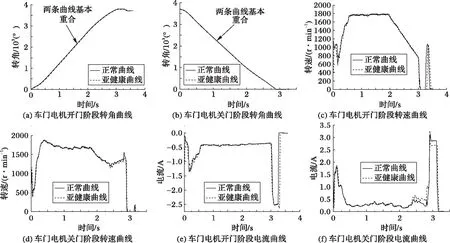
图7 车门电机数据 Fig. 7 Data of door motor
3.2 距离表示的特征集参数分析
利用多尺度滑动窗口的特征提取算法对8种亚健康以及对应的正常数据进行分析,每组数据分别可以获得600多个开门特征及关门特征。最终获得的整体的特征已经达到1 200个之多,构成的特征维数很高,各组特征之间的相关性较大,且存在大量冗长信息(主要存在于开关门过程中的均速段)。直接将这些数据放入分类器进行模式识别,不仅给分类的过程造成较大的负担,同时还影响分类的准确率。主成分分析(PCA)[14]通过映射的方法将特征变换为维数较少的新特征,在保留主要特征的同时极大地降低特征的维数。
针对开关门整体特征参数,通过求解协方差矩阵的特征值和对应的特征向量,确定各主要成分。图8列出了前10个主成分的贡献率随主成分变化趋势图。
由图8分析得到,从第5个主成分开始,贡献率的变化趋势已趋于平稳并逐渐接近于0。累计经过主成分变换后各特征值的贡献率,前4个特征值累计贡献率达到73%,相对的前20个累计贡献率为90%。由此可见,前4个主成分可以很好地表示原本数据的大部分特征。为了进一步反映各主成分对车门亚健康状态的敏感程度,图9给出了前4个主成分在不同的亚健康状态下的分布。由图9可知,第一个特征拥有着最高的贡献率,能准确地区分对中尺寸变化大、对中尺寸变化小、上滑道外移和正常这4个状态,对其他几种状态存在着混叠现象;其他3个特征仅对部分的亚健康状态有着很好的区分度,对其余状态存在着明显的混叠以及波动较大。结合这些特征的分布情况,可以发现区分度最好的亚健康状态为对中尺寸变化小、对中尺寸变化大、压轮过压和正常状态,其次为上滑道外移、V型异常和下挡销纵向干涉,而电机组松动和下挡销横向干涉的区分度较差。综上所述,将电机组松动和下挡销横向干涉归为Ⅱ类亚健康,其他6种归为Ⅰ类亚健康;在分层识别算法,首先对6种Ⅰ类亚健康进行区分,接着结合基础特征,对正常数据和剩下的2种Ⅱ类亚健康状态作进一步识别。
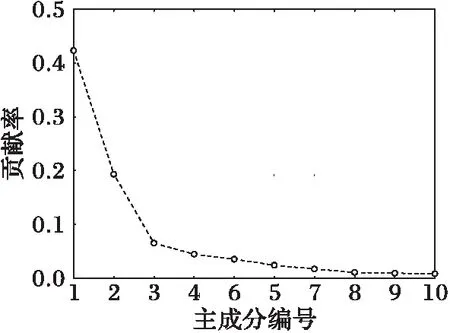
图8 贡献率随特征变化趋势 Fig. 8 Trend of contribution rate with principal components changing
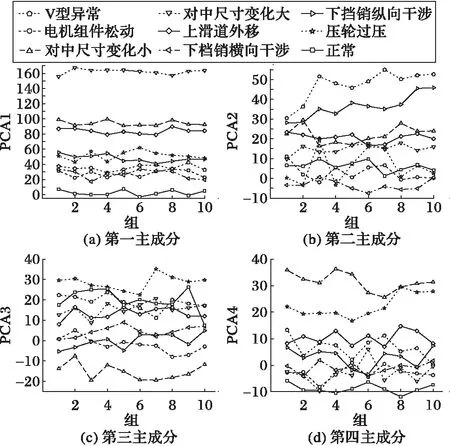
图9 前4个主成分在各亚健康状态下的分布 Fig. 9 Distribution of first four principal components in different sub-health states
3.3 亚健康状态的识别
3.3.1 基于距离表示特征的亚健康状态识别
为了进一步验证距离表示特征集的有效性,采用几个常用分类器对其进行分类。选取3.1节中的8种正常数据和亚健康数据,其中一半用作训练集,另一半用作测试集,得到总的训练集数据330个,测试集数据326个,实验分为3次,分别依据车门开门特征、关门特征以及整体特征进行识别。实验过程中选择降维后的前20个主成分进行训练识别,分类器分别为1NN(k-Nearest Neighbor,其中k=1)[15]、人工神经网络(Artificial Neural Network, ANN)[2]和支持向量机(Support Vector Machine, SVM)[12]。其中:SVM选择高斯核,惩罚系数C为10;ANN使用多层感知器拓扑结构,节点输出函数采用Sigmoid函数。
表2中的识别率为测试集正确识别的个数占测试集总个数的比例,基于距离的特征集通过对电机数据的字符化处理和序列中极值点的挖掘,其识别的准确率要高于传统特征集。从各特征的识别准确率来看,开关门整体特征要比单个特征拥有更好的识别结果。各分类器识别的准确率相差不大,SVM识别的准确率比其他分类器略高。由于Ⅱ类亚健康与正常数据比较接近,错误识别主要发生在某些正常数据被错分成Ⅱ类亚健康。
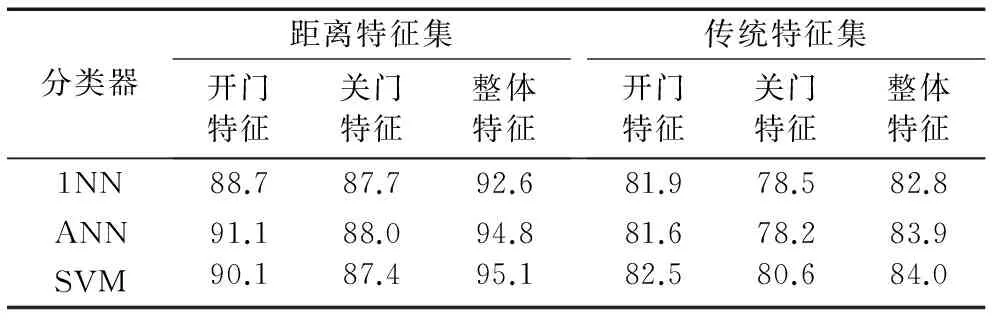
表2 不同特征的识别结果 %Tab. 2 Results of classification based on different feature %
3.3.2 基于融合特征的分层亚健康状态识别
采用分层亚健康识别模型对同样的数据进行识别。在第1层训练中,将Ⅱ类亚健康和正常数据看作一类,依据基于距离特征集,对其他6种Ⅰ类亚健康进行识别;在第2层的识别中,融合基于距离的特征集和基础特征集,对正常数据和Ⅱ类亚健康进一步判断。各层分类器均采用SVM作为分类器,核函数使用高斯核,第1层中惩罚系数C为10,第2层中惩罚系数C为1。测试集数据每层的识别结果如表3所示。

表3 分层亚健康状态识别结果 %Tab. 3 Results of hierarchical sub-health state identification %
表3中第1层的识别率表示第1层中测试集正确识别的个数占测试集总个数的比例;第2层对Ⅱ类亚健康进一步判断,识别率表示两层中正确识别的个数之和占测试集总数的比例。分析表3可知,与3.3.1节的识别结果相比,分层亚健康识别模型的开门、关门和整体特征的识别率都有所提高。在第1层中,将区分度较差的亚健康数据和正常数据归为一类,先区分较为明显的Ⅰ类亚健康,故三种特征的识别率都比较高,其中整体特征在这层的识别结果全部正确;第2层中,亚健康差别较小,错误明显增多,识别率下降较大。最终本文方法的识别率可达到99%,测试样本中仅有3个下档销横向干涉被识别错误。由此可见,采用分层识别的模型能够对亚健康数据做到更加准确的区分。
4 结语
本文提出了一种基于时间序列数据挖掘的轨道车辆门亚健康状态识别的方法,通过对实测地铁门电机数据的分析得到以下结论:
1)采用多尺度滑动窗口的方法并结合ESAX字符化算法对地铁门电机数据进行字符化,有效地捕捉了时间序列中的极值点信息,同时能够多层次地挖掘出车门运行过程中不同阶段的信息。
2)将亚健康数据与模板曲线之间的距离作为特征集,减小实验中车门调整所带来的误差;同时使用主成分分析对特征降维并分析了前4种主成分在不同的亚健康状态下的分布,将实测的8种车门亚健康划分为Ⅰ类和Ⅱ类。
3)通过车门8种亚健康状态结果分析,表明分层亚健康识别模型比单个特征集有更好的分类效果,能够准确识别各种亚健康状态。
由于本文算法字符化后的字符串的长度较长,存在着效率较低的缺点,接下来的工作就是进一步提高算法实现的效率,以及对更多类型的亚健康状态进行分析。
参考文献(References)
[1] REN J B, LONG J, QIN Y, et al. Fault criticality evaluation of metro door based on WLSM and FWGM [C]// EITRT 2013: Proceedings of the 2013 International Conference on Electrical and Information Technologies for Rail Transportation, LNEE 288. Berlin: Springer, 2014, Ⅱ: 293-300.
[2] 朱兴统,熊建斌.基于PCA和BP神经网络的故障诊断仿真系统[J].自动化与仪器仪表,2015(12):47-48. (ZHU X T, XIONG J B. The fault diagnosis system based on PCA and BP neural network [J]. Automation & Instrumentation, 2015(12): 47-48.)
[3] 李海林,郭崇慧,杨丽彬. 基于时间序列数据挖掘的故障检测方法[J].数据采集与处理,2016,31(4):782-790. (LI H L, GUO C H, YANG L B. Fault detection algorithm based on time series data mining [J]. Journal of Data Acquisition and Processing, 2016, 31(4): 782-790.)
[4] 胡为,高雷,傅莉.基于最优阶次HMM的电机故障诊断方法研究[J].仪器仪表学报,2013,34(3):524-530. (HU W, GAO L, FU L. Research on motor fault detection method based on optimal order hidden Markov model [J]. Chinese Journal of Scientific Instrument, 2013, 34(3): 524-530.)
[5] GRUBB H J, WALDEN A T. Characterizing seismic time series using the discrete wavelet transform [J]. Geophysical Prospecting, 2010, 45(2): 183-205.
[6] 林意,王智博.基于一阶滤波的时间序列分段线性表示方法[J].计算机工程,2016,42(9):151-157.(LIN Y, WANG Z B. Time series piecewise linear representation method based on first-order filtering [J]. Computer Engineering, 2016, 42(9): 151-157.)
[7] LIN J, KHADE R, LI Y. Rotation-invariant similarity in time series using bag-of-patterns representation [J]. Journal of Intelligent Information Systems, 2012, 39(2): 287-315.
[8] LIN J, KEOGH E, WEI L, et al. Experiencing SAX: a novel symbolic representation of time series [J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144.
[9] LKHAGVAK B, SUZUKI Y, KAWAGOE K. Extended SAX: extension of symbolic aggregate approximation for financial time series data representation [EB/OL]. [2017- 03- 16]. http://www.ieice.org/iss/de/DEWS/DEWS2006/doc/4A-i8.pdf.
[10] 田再克,李洪儒,孙健,等.基于改进MF-DFA和SSM-FCM的液压泵退化状态识别方法[J].仪器仪表学报,2016,37(8):1851-1860. (TIAN Z K, LI H R, SUN J, et al. Degradation state identification method of hydraulic pump based on improved MF-DFA and SSM-FCM [J]. Chinese Journal of Scientific Instrument, 2016, 37(8): 1851-1860.)
[11] LAI C-P, CHUNG P-C, TSENG V S. A novel two-level clustering method for time series data analysis [J]. Expert Systems with Applications, 2010, 37(9): 6319-6326.
[12] 陈立江,毛峡,MITSURU I,等.基于Fisher准则与SVM的分层语音情感识别[J].模式识别与人工智能,2012,25(4):604-609. (CHEN L J, MAO X, MITSURU I, et al. Multi-level speech emotion recognition based on Fisher criterion and SVM [J]. Pattern Recognition and Artificial Intelligence, 2012, 25(4): 604-609.)
[13] SIIRTOLA P, KOSKIMAKI H, HUIKARI V, et al. Improving the classification accuracy of streaming data using SAX similarity features [J]. Pattern Recognition Letters, 2011, 32(13): 1659-1668.
[14] 律方成,金虎,王子建,等.基于主成分分析和多分类相关向量机的GIS局部放电模式识别[J].电工技术学报,2015,30(6):225-231. (LYU F C, JIN H, WANG Z J, et al. GIS partial discharge pattern recognition based on principal component analysis and milticlass relevance vector machine [J]. Transactions of China Electrotechnical Society, 2015, 30(6): 225-231.)
[15] 陈法法,汤宝平,苏祖强,等.基于等距映射与加权KNN的旋转机械故障诊断[J].仪器仪表学报,2013,34(1):215-220. (CHEN F F, TANG B P, SU Z Q, et al. Rotation machinery fault diagnosis based on isometric mapping and weightedKNN [J]. Chinese Journal of Scientific Instrument, 2013, 34(1): 215-220.)
XUEYu, born in 1992, M. S. candidate. His research interests include data mining, pattern recognition.
MEIXue, born in 1975, Ph. D., associate professor. Her research interests include image processing, pattern recognition.
ZHIYouran, born in 1984, Ph. D., associate professor. His research interests include fire science, pattern recognition.
XUZhixin, born in 1970, Ph. D. His research interests include fault diagnosis, data mining.
SHIXiang, born in 1956, M. S. His research interests include fault diagnosis, data mining.

