基于联合概率矩阵分解的个性化试题推荐方法

李 全，刘兴红，许新华，林 松

(湖北师范大学 教育信息与技术学院，湖北 黄石 435002)

0 引言

随着网络技术和教育信息化的不断发展，人们的学习不再受时间和空间的限制。智能教育和在线教育能够便捷地为学生提供试题练习，帮助学生巩固学习知识，但是随着试题资源数量爆炸式的增长，学生很难在海量的试题资源中找到合适的试题，因此，在智能教育系统中，如何为学生推荐符合其学习特征的试题是一个重要的问题[1]。

目前，研究者将推荐系统的相关技术应用到试题推荐中，并开展了初步的研究工作。现有的试题推荐方法一般可以分为3类：基于内容的推荐方法[2]、基于协同过滤推荐方法[3-5]和混合推荐方法[6]。在这些推荐方法中，基于协同过滤的推荐是应用最广泛的推荐方法。该方法主要包括基于邻域协同过滤和基于模型协同过滤。基于邻域协同过滤又可以分为基于用户(User-based)协同过滤和基于项目(Item-based)协同过滤，但它们通常面临着冷启动、数据稀疏、算法可扩展性差等问题[7]。为了进一步解决数据稀疏性和冷启动等问题，一些现代推荐系统采用基于模型协同过滤的推荐方法中矩阵分解技术进行推荐。矩阵分解技术包括奇异值分解(Singular Value Decomposition, SVD)[8]、非负矩阵分解(Non-negative Matrix Factorization, NMF)[9]和概率矩阵分解(Probabilistic Matrix Factorization, PMF)[10]等，其中以概率矩阵分解应用最为广泛。它可以将一个高维的学生-试题得分矩阵分解为两个学生和试题的低维矩阵，然后利用两个低维矩阵的乘积来预测学生在试题上的得分，最后根据预测的得分进行试题推荐，但该方法只能结合学生和试题两方面的信息进行两维分解,而没有考虑学生的知识点掌握信息，因此，在应用到试题推荐时,可能导致试题推荐结果不合理、不可靠和缺少解释性等问题[11]。为了进一步提高试题推荐方法的性能，针对以上问题，本文提出了一种基于联合概率矩阵分解的个性化试题推荐方法。首先，通过认知诊断模型对学生进行建模，得到学生的知识点掌握信息；接着，将试题-知识点信息和学生-知识点信息融入到基于学生试题得分概率矩阵分解方法中，实现联合概率矩阵分解，得到用户特征矩阵和试题特征矩阵。然后，根据用户特征矩阵和试题特征矩阵计算学生对试题的预测得分；最后，把相应难度范围的试题推荐给学生。该方法保证了试题推荐结果的可解释性和合理性。实验结果表明，本文提出的方法在不同难度的试题推荐准确率上要优于传统的协同过滤算法和已有的矩阵分解算法。

1 相关工作

近年来，有学者将传统的推荐技术应用到智能教育和在线教育的相关研究中。而在这些推荐方法中，基于协同过滤的推荐是应用最广泛的推荐方法。该方法主要包括基于邻域协同过滤和基于模型协同过滤。基于邻域协同过滤算法通过分析和目标学生的相似学生来对目标学生进行推荐。文献[12]针对大学体育课程教育和教学问答应用，从功能、处理方法等角度设计推荐系统架构；但在推荐方法上，并未考虑数据稀疏性对推荐方法的影响。文献[13]引入数据挖掘技术，挖掘历史行为记录中的潜在规则，为学习者提供个性化学习指导；但挖掘出的规则局限于已有数据，在数据稀疏情况下，对于新的资源，由于缺乏行为数据而不能推荐给用户。文献[14]提出了一种在线学习背景下基于模糊树匹配用户学习材料个性化推荐方法。文献[15]提出了一种融合不同学生的学习兴趣并向同一组学生进行个性化学习材料推荐的方法；但在预测学生表现时，会丢失学生自身的一些学习特征。因此，基于邻域协同过滤推荐算法通常在网络教育应用中存在一定的局限性。

目前，基于模型协同过滤的推荐方法中矩阵分解算法逐渐成为了教育应用中最为广泛的算法，因为矩阵分解算法比传统的推荐技术具有更好的推荐精度[16]。它通过构造学生和试题的低维矩阵，然后利用两个低维矩阵的乘积来预测学生在试题上的得分，最后根据预测的得分进行试题推荐；但是该方法只能结合学生和试题两方面的信息进行两维分解，并且该方法在应用到试题推荐时忽略了学生试题相关的知识点信息，使系统无法向学生解释推荐某一试题的原因；此外通过该方法向学生推荐的试题可能对学生并没有帮助。因此，如何结合学生自身的特性和相似学生的做题情况提高试题推荐合理性和可靠性成为了一个重要的研究问题。

在认知心理学中，认知诊断模型可以较好地从知识点层面对学生的认知状态进行建模[17]。现有的认知诊断模型包括连续型和离散型。其中，项目反应理论(Item Response Theory, IRT)是一种典型的连续型认知诊断模型。它根据学生答题情况，通过对试题和学生进行联合建模，来推出试题参数及学生潜在能力[18]。DINA模型(Deterministic Inputs，Noisy “And” gate model)是一种典型的离散型认知诊断模型。该模型将学生描述成一个多维的知识点掌握向量，从学生实际作答结果入手进行诊断[19]。由于DINA模型简单，参数的可解释性较好，且DINA模型的复杂性不受属性个数的影响[20]，因此本文选择DINA模型作为认知诊断模型对学生进行建模，得到学生的知识点掌握信息，并将其融入到学生试题概率矩阵分解方法中，从而提出了一种基于联合概率矩阵分解的个性化试题推荐方法。

2 基于联合概率矩阵分解的个性化试题推荐

2.1 问题的形式化定义

为了便于形式化描述，本文的符号标记如表1所示。

表1 符号表Tab. 1 Notations

已知学生集合US={u1,u2,…,um}，试题集合TS={t1,t2,…,tn}，知识点集合BS={b1,b2,…,bl}，学生试题得分矩阵R=[rij]m×n表示m个学生做n道试题，其中，rij=1表示学生ui答对试题tj；rij=0表示学生ui答错试题tj。试题知识点矩阵Q=[qjk]n×l表示n道试题和l个知识点相关联，其中，qjk=1表示试题tj考查知识点bk；qjk=0表示试题tj未考查知识点bk。

2.2 QueRec方法整体框架

本文提出的基于联合概率矩阵分解的个性化试题推荐方法(QueRec)的整体框架如图1所示。

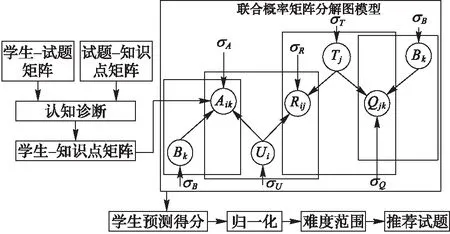
图1 QueRec整体框架 Fig. 1 Whole framework of QueRec

从图1中可以看出，该推荐方法主要步骤如下：

1)输入学生做题的学生-试题得分矩阵和由领域专家标注的试题-知识点关联矩阵。

2)使用DINA模型对学生进行建模，获取学生-知识点掌握信息矩阵。

3)将试题-知识点矩阵和学生-知识点矩阵融入到基于学生试题得分概率矩阵分解方法中，实现联合概率矩阵分解，得到用户特征矩阵和试题特征矩阵。

4)根据用户特征矩阵和试题特征矩阵计算得到学生的预测得分，并将预测得分归一化到[0,1]范围。

5)设置待推荐试题的难度范围[λ1,λ2],根据学生预测得分情况，把相应难度范围内的试题推荐给学生。

2.3 构造学生-知识点矩阵

为了得到学生的个性化状态，采用DINA模型获取学生知识点掌握信息A=[aik]m×l。DINA模型通过学生试题矩阵R和试题知识点矩阵Q对学生进行建模，即对每一个学生ui都可以得到一个知识点掌握向量αi={ai1,ai2,…,ail}，其中aik=1表示学生ui掌握知识点bk，aik=0表示学生ui没有掌握知识点bk。所有学生的知识点掌握向量α={α1,α2,…,αm}。

学生的潜在作答情况如式(1)所示：

(1)

ηij=1表示学生ui掌握了试题tj考核的所有知识点;ηij=0表示学生ui没有掌握试题tj考核的所有知识点。此外，为了在真实状态下表示学生答题情况，DINA模型还引入了失误率和猜测率。失误率表示学生掌握了试题考查的所有知识点，存在因为粗心导致答题错误，如式(2)所示：

sj=p(rij=0|ηij=1)

(2)

猜测率表示学生没有掌握试题考查的所有知识点，处在一定的概率因为猜测导致答题正确，如式(3)所示：

gj=p(rij=1|ηij=0)

(3)

因此学生ui在试题tj上正确作答的概率如式(4)所示：

(4)

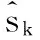
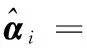
(5)

2.4 联合概率矩阵分解图模型

本文提出的基于联合概率矩阵分解的个性化试题推荐的图模型如图2所示。

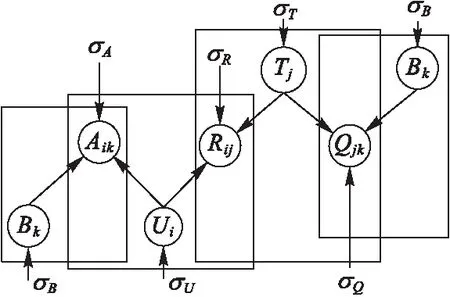
图2 联合概率矩阵分解图模型 Fig. 2 Graph model of unified probalilistic matrix factorization

联合概率矩阵分解图模型基于以下假设：

1)假设Ui、Tj、Bk的先验概率服从高斯分布且相互独立，即：

(6)

(7)

(8)

其中:N(x|μ,σ2)表示均值为μ，方差为σ2的正态分布的概率密度函数，I为单位矩阵。

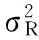
(9)

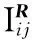
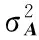
(10)

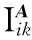
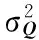
(11)

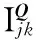
学生在试题上的得分受学生在试题所关联知识点上的掌握程度的影响，所以该算法将学生试题关系矩阵的分解、试题知识点关系矩阵分解和学生知识点关系矩阵的分解整合起来，通过学生特征矩阵和试题特征矩阵进行连接。由如图2可以推到出U、T和B的后验概率分布函数。后验分布函数的对数函数满足式(12)：

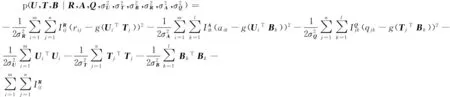
(12)

其中：d表示特征向量的维数，C是常量。最大化式(12)可视为无约束优化问题，最小化式(13)等价于最大化式(12):

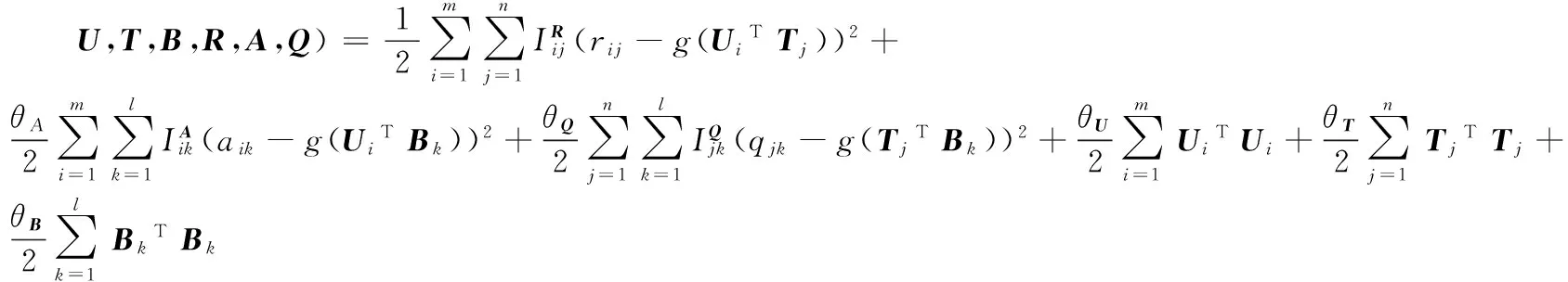
(13)

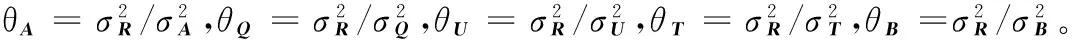
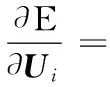
(14)

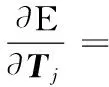
(15)

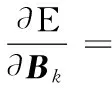
(16)

2.5 时间复杂度分析

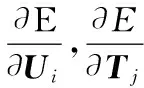
2.6 试题推荐

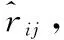
(17)

(18)

该公式表示：如果学生的预测得分越高，则待推荐试题的难度系数越低；如果学生的预测得分越低，则待推荐试题的难度系数越高。在进行试题推荐时，先要设定推荐试题的难度范围λ1和λ2(0<λ1<λ2<1)作为试题推荐难度的边界。QueRec方法可以根据待推荐试题的难度系数为学生推荐相应难度范围内的试题，保证了试题推荐结果的可解释性和合理性。

3 实验与结果分析

3.1 实验数据

本文所用的实验数据来自于某市高校学生数据库考试的真实数据，考试的数据真实反映了学生对试题的掌握程度。原始数据集包括203个学生，46道试题，18个知识点，8 243个学生试题得分信息，763个试题与知识点关联信息。

3.2 评价指标

本文选用推荐系统领域常用F1值作为评价指标。F1值综合了信息检索领域中的准确率(Precision)和召回率(Recall)。F1值越高，表明推荐算法的准确率越高。具体F1值、准确率和召回率的定义如式(19)所示:

(19)

其中：Precison表示推荐的试题中真正符合学生兴趣的试题所占的比例，Recall表示推荐的试题中符合学生兴趣的占测试集中所有试题的比例，X表示推荐的结果集，Y表示测试集。

3.3 方法比较

为了验证QueRec方法的预测准确率，将其与基于用户(User-Based)协同过滤方法、基于项目(Item-Based)协同过滤方法和基于概率矩阵分解(PMF)方法进行比较。在实验过程中，从数据集中分别抽取90%、70%、50%和30%作为训练数据，在数据稀疏程度不同时，比较算法的效果。90%的训练数据表示从数据集中随机抽取90%的数据来预测剩下的10%的数据。同时，为了降低算法的复杂度，通过反复实验测试，在QueRec方法中，将θU、θT、θB均设置为0.001，θA设置为0.5，θQ设置为1，潜在特征向量维数为10，该方法效果最好。

3.4 实验结果分析

3.4.1 不同难度试题推荐对比实验

在比较不同难度试题推荐效果实验中，根据难度范围，将待推荐试题分为简单试题和困难试题两类，其中难度范围λ∈[0,0.6]的待推荐试题为简单试题，即学生的预测得分较高的试题；难度范围λ∈(0.6,1]的待推荐试题为困难试题，即学生的预测得分较低的试题。在实验中分别向学生推荐6道简单试题和6道困难试题，将QueRec与其他3种方法进行对比实验。实验结果如表2所示。

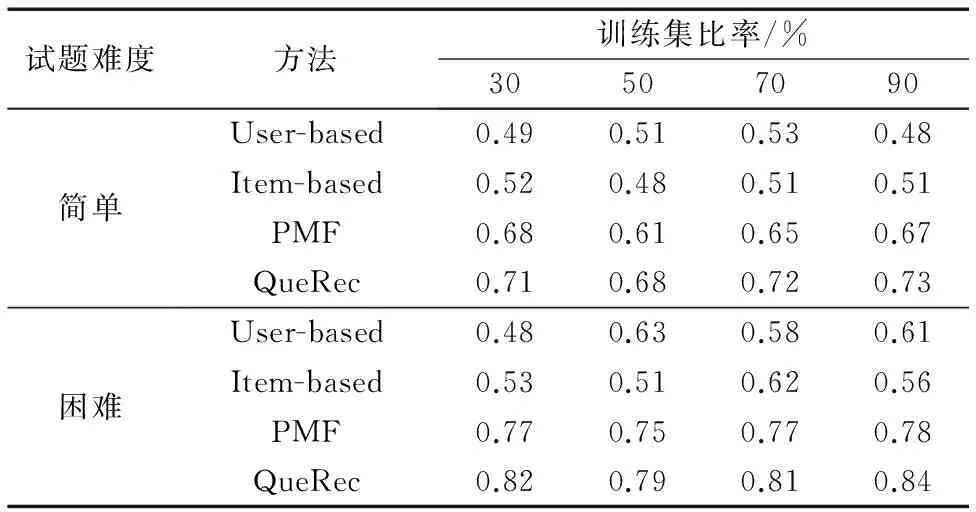
表2 不同难度试题预测效果的F1值Tab. 2 F1 value of prediction effect of different difficulty test questions

利用不同稀疏程度的训练集对以上算法进行实验，由表2可知，随着训练集的增大，QueRec方法在简单试题和困难试题的推荐准确率上比其他的3种算法高。在推荐简单试题时F1值比其他3种算法提高了4.2%～6.8%。在推荐困难试题时F1值比其他3种算法提高了5.6%～8.3%。

3.4.2 参数θA和θQ对方法的影响

参数θA决定了学生-知识点矩阵对算法效果的影响，参数θQ决定了试题-知识点矩阵对算法效果的影响。当θA和θQ都设置为0时，试题推荐方法不考虑学生与知识点之间以及试题与知识点之间的相互关系，只考虑学生和试题的得分矩阵。当θA和θQ越大，学生与知识点之间以及试题与知识点之间的相互关系对算法的作用越大。当测试θA对算法的影响时，将θU、θT、θB分别设置为0.001，θQ设置为1，具体结果如图5和图6所示。当测试θQ对算法的影响时，将θU、θT、θB分别设置为0.001，θA设置为0.5，具体结果如图3～6所示。

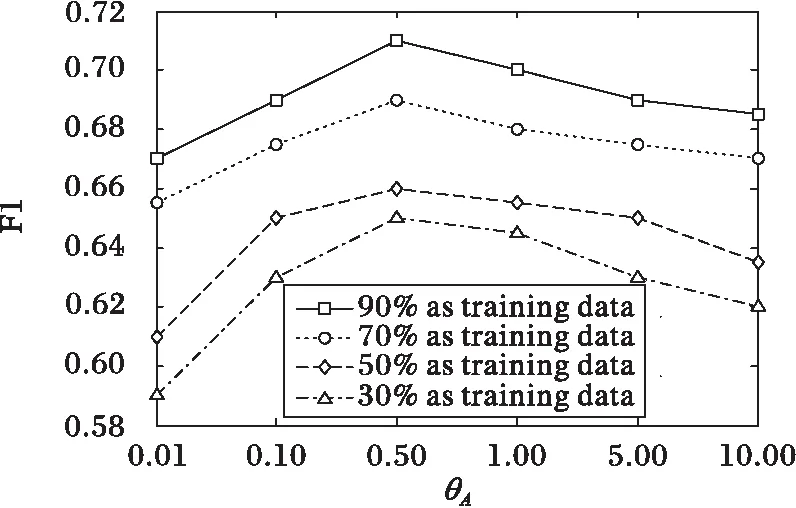
图3 简单试题推荐时参数θA对F1值的影响 Fig. 3 Impact of θA on F1 (simple question recommendation)

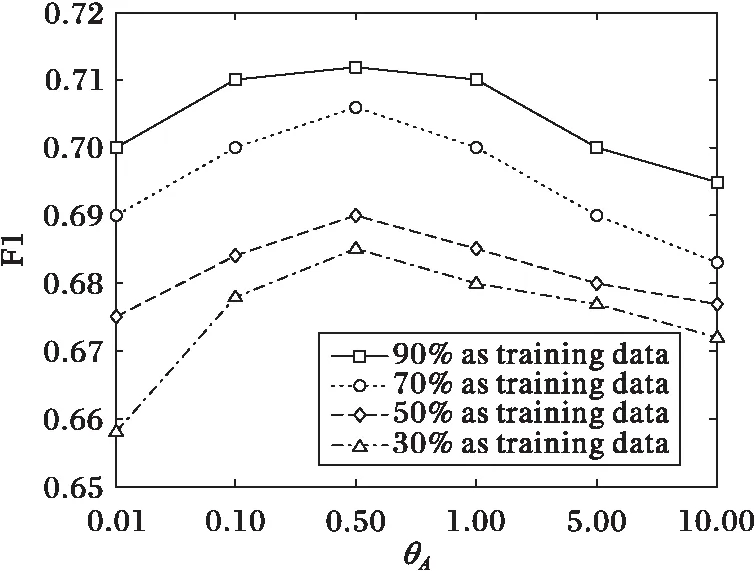
图4 困难试题推荐时参数θA对F1值的影响 Fig. 4 Impact of θA on F1 (difficult question recommendation)

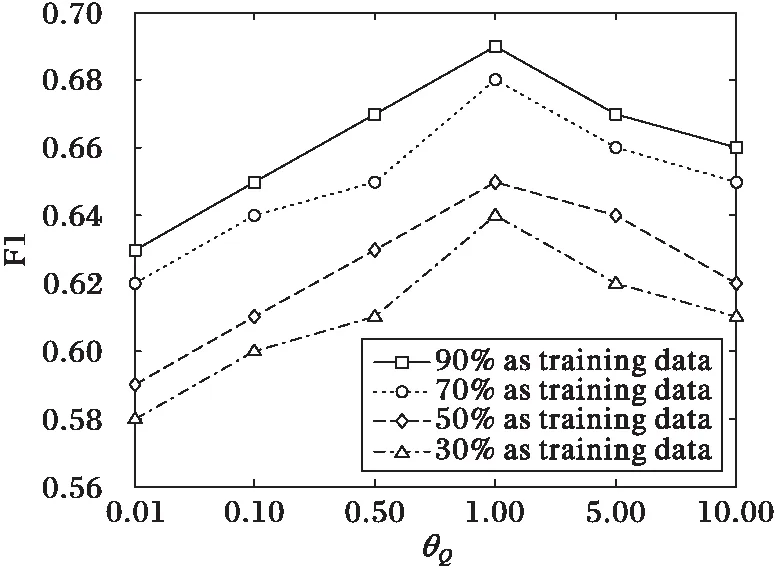
图5 简单试题推荐时参数θQ对F1值的影响 Fig. 5 Impact of θQ on F1 (simple question recommendation)

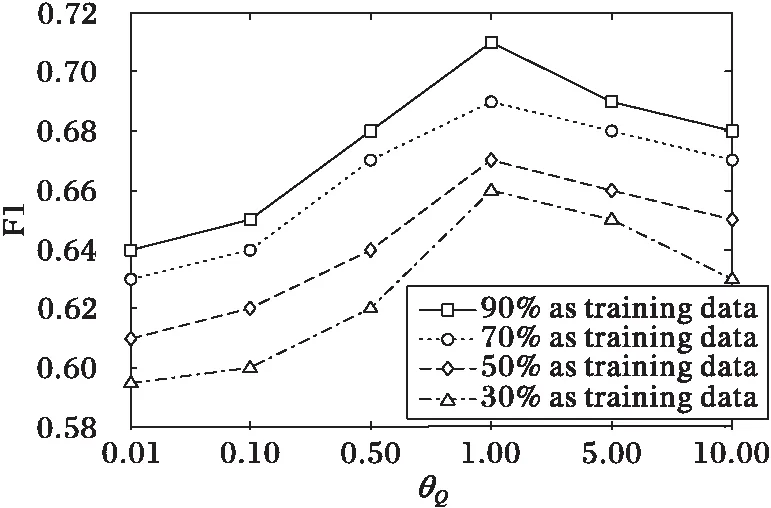
图6 困难试题推荐时参数θQ对F1值的影响 Fig. 6 Impact of θQ on F1 (difficult question recommendation)

由图3～6可以得出以下结论：参数θA和θQ的值对算法推荐准确率的影响是比较大的。通过进一步观察发现，随着参数θA或者θQ的增加，算法的F1值先增加；当θA=0.5或者θQ=1时，F1值取得最大值；但当θA超过0.5或者θQ超过1时，F1值逐渐降低，QueRec方法的推荐效果开始下降。主要原因是由于θA或者θQ过大时，引起了QueRec方法的过拟合，导致推荐准确率的下降。

4 结语

本文对智能教育和在线教育中的试题推荐方法进行了研究。本文在概率矩阵分解方法的基础上，通过认知诊断模型对学生进行建模，将试题-知识点信息和学生-知识点信息融入到基于学生试题得分概率矩阵分解方法中，提出了一种基于联合概率矩阵分解的个性化试题推荐方法。实验结果表明，与其他传统推荐方法相比，本文所提方法在不同难度范围的试题推荐上均取得了较好的推荐结果；另外，通过对算法时间复杂度的分析，表明该方法可以应用于大规模数据集。在下一步的研究工作中，将更加深入地研究认知诊断模型对试题推荐方法的影响，以期进一步提高该推荐算法的精度和性能。

参考文献(References)

[1] VESIN B, IVANOVIC M, BUDIMAC Z, et al. E-learning personalization based on hybrid recommendation strategy and learning style identification [J]. Computers and Education, 2011, 56(3): 885-899.

[2] ZHAO W, WU R, LIU H. Paper recommendation based on the knowledge gap between a researcher’s background knowledge and research target [J]. Information Processing and Management, 2016, 52(5): 976-988.

[3] BOGERS T, van den BOSCH A. Recommending scientific articles using citeulike [C]// Proceedings of the 2008 ACM Conference on Recommender Systems. New York: ACM, 2008: 287-290.

[4] TIAN G, JING L. Recommending scientific articles using birelational graph-based iterative RWR [C]// Proceedings of the 2013 7th ACM Conference on Recommender Systems. New York: ACM, 2013: 399-402.

[5] LAI C H, LIU D R, LIN C S. Novel personal and group-based trust models in collaborative filtering for document recommendation [J]. Information Sciences, 2013, 239(8): 31-49.

[6] SUN J, MA J, LIU Z, et al. Leveraging content and connection for scientific article recommendation in social computing contexts [J]. The Computer Journal, 2014, 57(9): 1331-1342.

[7] CREMONESI P, TURRIN R. Analysis of cold-start recommendations in IPTV system [C]// Proceedings of the 2009 3rd ACM Conference on Recommender Systems. New York: ACM, 2009: 233-236.

[8] GOLUB G, KAHAN K. Calculating the singular values and pseudo-inverse of a matrix [J]. Journal of the Society for Industrial and Applied Mathematics, 1965,2(2): 205-224.

[9] LEE D D, SEUNG H S. Algorithms for non-negative matrix factorization [C]// Proceedings of the 2001 13th International Conference on Neural Information Processing Systems. Cambridge, MA: MIT Press, 2001: 535-541.

[10] SALAKHUTDINOV R, MNIH A. Probabilistic matrix factorization[C]// Proceedings of the 2007 20th International Conference on Neural Information Processing Systems. Vancouver, British Columbia: Curran Associates Inc., 2007: 1257-1264.

[11] KOREN Y, BELL R, VOLINSKY C. Matirx factorization for recommender systems [J]. IEEE Computer, 2009, 42(8): 30-37.

[12] SOUALI K, AFIA A E, FAIZI R, et al. A new recommender system for e-learning environments [C]// Proceedings of the 2011 International Conference on Multimedia Computing and System. Piscataway: IEEE, 2011: 1-4.

[13] 张海东,倪晚成,赵美静,等.面向基础教育阶段的教学资源推荐系统[J].计算机应用,2014,34(11):3353-3356.(ZHANG H D, NI W C, ZHAO M J, et al. Teaching resources recommendation system for K12 education [J]. Journal of Computer Applications, 2014, 34(11): 3353-3356.)

[14] WU D, ZHANG G, LIU J. A fuzzy tree matching-based personalised e-learning recommender system [J]. IEEE Transactions on Fuzzy Systems, 2015, 23(6): 2412-2426.

[15] DWIVEDI P, BHARADWAJ K K. E-learning recommender system for a group of learners based on the unified learner profile approach [J]. Expert Systems, 2015, 32(2): 264-276.

[16] XU W, CAO J, HU L, et al. A social-aware service recommendation approach for mashup creation [C]// Proceedings of the 2013 IEEE 20th Internationnal Conference on Web Services. Washington, DC: IEEE Computer Society, 2013: 107-114.

[17] TAMHANE A, IKBAL S, SENGUPTA B, et al. Predicting student risks through longitudinal analysis [C]// Proceedings of the 2014 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York: ACM, 2014: 1544-1552.

[18] 康春花,孙小坚,顾士伟,等.多水平多维IRT模型在学业质量监测中的应用[J].江西师范大学学报(自然科学版),2016,40(2):133-139.(KANG C H, SUN X J, GU S W, et al. The application of multilevel multidemensional IRT model in academic quality monitoring test [J]. Journal of Jiangxi Normal University (Nature Science Edition), 2016, 40(2): 133-139.)

[19] OZAKI K. DINA models for multiple-choice items with few parameters:considering incorrect answers [J]. Applied Psychological Measurement, 2015, 39(6): 431-447.

[20] de la TORRE J. The generalized DINA model framework [J]. Psychometrika, 2011, 76(2): 179-199.

This work is partially supported by the Education Science “Twelfth Five-Year” Planning Project of Hubei Province (2011-B130), the Planning Project of Science and Technology of State Archives Bureau (2016-x-51), the Planning Project of Outstanding Young and Middle-aged Scientific and Technological Innovation Team of Universities and Colleges of Hubei Province (T201515), the Science and Technology Project of Education Department of Hubei Province (D20142504).

LIQuan, born in 1982, M. S., lecturer. His research interests include machine learning, data mining.

LIUXinghong, born in 1969, M. S., professor. Her research interests include big data, education informationization.

XUXinhua, born in 1968, M. S., professor. His research interests include database, data mining.

LINSong, born in 1978, M. S., lecturer. His research interests include search engine, data mining.