基于均匀局部搜索和可变步长的萤火虫算法
王晓静,彭 虎,邓长寿,黄海燕,张 艳,谭旭杰
(九江学院 信息科学与技术学院,江西 九江 332005)
0 引言
Yang[1]研究了萤火虫个体间相互吸引与发光亮度的关联关系,以及萤火虫的移动特性,于2008年提出了一种新型群智能优化算法,即萤火虫算法(Firefly Algorithm, FA)。FA的基本思想是模拟萤火虫的发光特性在一定区域内寻找伙伴,向位置较优的萤火虫移动,以达到寻优的目的。萤火虫算法操作简单、参数少、收敛速度较快,已被成功地用于路径优化[2]、电频谱分配[3]、水资源优化配置[4]、板料成形优化[5]、工程管柱设计[6]等优化问题中,从而引起了国内外学者的广泛关注,成为智能计算领域的一个研究热点。
萤火虫算法也存在一些不足,比如后期收敛速度慢、易陷入局部最优、寻优结果依赖于初始种群和参数设置等。许多学者对其进行了各种改进。如臧睿等[6]将自适应惯性权重引入标准萤火虫算法,提高了算法的收敛速度。王翔等[7]设计了一种混沌局部搜索算子和替换算子,克服了萤火虫算法收敛速度慢和易于早熟的缺陷。Wang等[8]设计了随机吸引模型和三个邻域搜索策略,以及动态参数调整策略,提高了萤火虫算法的搜索精度,增强了算法的鲁棒性。Yu等[9-10]先后提出了基于个体最好位置与全局最好位置的步长设置策略[9],以及非线性动态调整步长策略[10],提高了搜索质量。刘金等[11]提出了图形处理器(Graphics Processing Unit, GPU)上的维度并行随机吸引策略萤火虫算法,降低了标准萤火虫算法的时间复杂度,提高了其优化能力。陆克中等[12]提出了一种基于全局信息共享的自适应FA,提高了收敛速度和收敛精度。
本文借鉴Peng等[13]提出的均匀局部搜索策略对差分进化(Differential Evolution, DE)算法的改进,在萤火虫种群中随机选择两个个体构成一个局部空间,利用均匀设计实验设计方法,在此空间中寻找一个最优个体并进行迭代,以达到增强局部开采能力的目的,从而提高算法的收敛性能。为了弥补局部搜索可能出现的局部最优和早熟的缺陷,考虑到萤火虫位置更新时在局部和全局之间的平衡性,引入Yu等[10]提出的非线性动态调整步长策略,利用当前迭代次数和最大迭代次数建立起非线性变化的步长值对算法进行改进。通过12个测试函数的验证,证明了改进算法的有效性,并针对不同维度问题中算法结果的差异,分析了原因并给出了解决办法。
1 标准FA
萤火虫算法用搜索空间中的所有可行解模拟夜空中的萤火虫个体,将问题的目标函数适应度值定义为萤火虫所处位置的相应解,将优化过程模拟成萤火虫个体的相互吸引和位置更新过程,将个体的优胜劣汰过程类比为搜索和优化过程中用好的可行解取代较差可行解的迭代过程。算法涉及两个关键因素,即萤火虫个体的发光亮度和相对吸引度。萤火虫的发光亮度取决于自身所在位置的目标值,亮度越高表示所处的位置越好,即目标值越佳。吸引度与亮度相关,越亮的萤火虫拥有越高的吸引力,可以吸引视线范围内亮度比其弱的萤火虫往这个方向移动。如果发光亮度相同,则萤火虫各自随机移动。亮度和吸引度与萤火虫之间的距离成反比,都随着距离的增加而减小。
1.1 标准FA的基本思想
标准FA涉及的主要公式包括相对荧光亮度公式、相对吸引度公式和位置更新公式[14]如下所示:
荧光亮度为:
I(r)=I0e-γr
(1)
其中:I0为萤火虫的最大荧光亮度,即r=0处的荧光亮度,与目标函数值相关,目标函数值越优自身亮度越高;γ为光强吸收系数,以体现光强的减弱特性,在多数问题中γ∈[0.01,100];r通常为萤火虫i与j间的欧氏距离。
吸引度为:
β(r) =β0e-γr2
(2)
其中:β0为最大吸引度,即r=0处的吸引度;γ为光强吸收系数。
寻优过程中萤火虫j受萤火虫i的吸引,从而向萤火虫i靠近的位置更新公式为:
xj(t+ 1) =xj(t) +β(xi(t)-xj(t)) +αεj
(3)
其中:xj(t+ 1)为萤火虫xj第t+1次移动后的位置;α为步长因子,是[0,1]上的常数;ε为[0,1]上服从高斯分布的随机因子。
1.2 标准FA步骤
在以上3个公式的基础上,标准萤火虫算法通过算法1的步骤完成寻优过程。
算法1 标准FA。
1)
选取适应度函数f(X),X= (x1,x2,…,xd)T
2)
初始化萤火虫种群Xi(i=l, 2,…,n)
3)
初始化算法基本参数γ、β0、MaxFEs(最大评估次数)
4)
5)
While (FEs 6) Fori=1∶n 7) Forj=1∶n 8) If (Ij>Ii) 1)模型坐标系:有限元模型坐标系:模型建立在直角坐标系(X,Y,Z)下,X 轴,沿河流方向并指向下游;Y 轴,垂直河流方向,指向山外;Z轴,竖直向上。 9) 根据式(2)计算相对吸引度 10) 根据式(3)萤火虫Xi在d维空间向xj移动 11) 计算适应度值f(X),更新荧光亮度 12) FEs=FEs+1 13) End if 14) End for 15) End for 16) 对所有萤火虫排序,确定当前最优位置 17) End while 18) 输出结果 均匀设计是Wang等[15]于1981年提出的科学实验方法,其实验思想是找到一些散布得更均匀的点集,利用这些点集来安排实验,使得实验结果既有代表性,又有相对较少的实验次数,从而减少实验时间,节约实验成本。在相同的均匀性前提下,正交设计实验次数的量级是O(q2),而均匀设计实验次数的量级是O(qlogq)。显然后者在实验次数上占很大优势。 Peng等[13]基于均匀设计提出了均匀局部搜索(Uniform Local Search, ULS)算子,并将之用于增强DE算法的局部开采能力,实验结果证明了ULS优异的局部搜索性能。均匀设计实验用均匀设计表来安排实验。均匀设计表是一个n行k列的表格,实验次数和水平个数相等,即n=q。用Un(qk)表示均匀设计表,其中U表示均匀设计,n表示实验次数,q表示每个因素的水平个数,k表示独立因素的最大个数[16]。 如文献[13]所述,ULS采用均匀设计表U7(76)进行实验,如表1所示。构建均匀设计表格的过程可参照文献[17]。从表1中可以看出,均匀设计允许每个因素拥有最大可能的水平数,因此,水平的数量等于实验数。研究中考虑到如下两点,首先,此处的均匀局部搜索方法中,表1的最后一行全是“7”,这代表了一个多余的原生个体;其二,经过多次实验验证,U6(66)是最合适的。因此,去掉均匀设计表U7(76)的最后一行从而构成U6(66)均匀设计表。每个因素有6个水平能从实验得到有效的信息,水平数大于6就没有必要,并且ULS还需要消耗更多的函数评估次数。 表1 均匀设计表U7(76)Tab. 1 Uniform design table U7(76) 以二维空间为例,如图1所示[13],均匀局部搜索就是在种群G中随机选择两个个体A和B执行一组实验,其搜索空间为A和B所构成的2维空间,将每一维均匀的分解成6个部分代表6个水平。依据均匀设计表的U6(66)的第一列和第二列,在A和B形成的搜索空间中生成了6个实验个体。假设C是这6个实验个体中的最优个体,那么C个体第一维的水平是1,第二维的水平是2。 在ULS算子中,如果问题的维数D大于6,则将D随机的分成6组,ULS将构建6个实验个体,花费6次评估次数。作为一种通用的局部搜索框架,ULS能应用到其他进化算法中以提高改善搜索能力。ULS算子的步骤如算法2所示[13]。 算法2 ULS算子步骤。 1) 输入:种群P、适应度函数评估次数FEs。 2) 从种群P中随机选择两个个体xi,G和xj,G。 3) 基于U6(66)在个体xi,G和xj,G之间构建6个实验个体Y1,Y2,…,Y6。 4) 评估目标函数值f(Y1),f(Y2),…,f(Y6)。 5) 从Y1,Y2,…,Y6中选取最优个体O。 6) If(f(xi,G)>f(O)) 7) xi,G=O 8) End if 9) FEs=FEs+6 10) 更新种群P,返回FEs。 图1 二维搜索空间中两个随机个体的均匀局部寻优示意图 Fig. 1 Illustration of uniform local search with two randomly chosen individuals in two-dimensional search space 萤火虫因亮度而相互吸引,如果某个个体周围有太多萤火虫亮度比其高,就会造成搜索过程中的震荡,这种无意义的震荡会增加时间复杂度。相反,如果这种吸引力很少,就会导致错过极优值而过早收敛。因此,吸引的数量和范围很重要。假如先把搜索过程限定在一定的范围内,搜索到该范围内的最优值,再进行扩展,以局部最优促成全局最优,就是一个合理的优化思路。ULS算子正好实现了这个思路。 在标准FA中,萤火虫因相互吸引而进行位置移动更新,之后再执行均匀局部搜索ULS算子进行一次搜索,利用该算子优异的局部搜索性能来提高FA的解质量。虽然ULS是一个有效的提高收敛速度的方法,但是它是一个相对贪婪的机制,执行次数越多,陷入局部极值的概率越大,因此,权衡收敛速度和种群多样性,每一代种群执行一次ULS。 在标准FA中,步长因子α的取值是固定的,这不能真正地反映搜索过程。通常较大的α取值适用于探索新的搜索空间,而较小的α取值适用于局部开采。因此,步长对于全局勘探和算法收敛有很大的影响。文献[10]中VSSFA(Variable Step Size Firefly Algorithm)中可变步长策略平衡了萤火虫的全局勘探和局部开采能力。在VSSFA中,步长α的调整公式如下: α(t)=0.4/(1+exp(0.015*(t-maxG)/3)) (4) 其中:t是当前迭代次数,maxG是最大迭代次数。在标准FA中,加入ULS算子,提出基于均匀局部搜索的萤火虫优化算法(Uniform local search Firefly Algorithm, UFA),该算法纯粹从搜索过程进行改进。其算法步骤在算法3的基础上略去第10)行即可。 在标准FA的基础上,使用以上步长调整策略,再利用均匀局部搜索算子ULS,提出了基于均匀局部搜索和可变步长的萤火虫优化算法(Firefly Algorithm based on Uniform local search and Variable step size, UVFA),从搜索过程和参数调整两个方面对标准FA进行优化,其算法的步骤如算法3所示。UVFA与标准萤火虫算法FA的区别主要体现在步骤的第10)行和第15)行,分别利用式(4)进行步长调整和利用均匀局部搜索算子增强局部寻优能力。 算法3 UVFA步骤。 1) 选取适应度函数f(X),X= (x1,x2,…,xd)T 2) 初始化萤火虫种群Xi(i=l, 2,…,n) 3) 初始化算法基本参数γ、β0、MaxFEs(最大评估次数) 4) FEs=n 5) While (FEs 6) Fori=1∶n 7) Forj=1∶n 8) If (Ij>Ii) 9) 根据式(2)计算相对吸引度 10) 根据式(4)计算步长α的值 11) 根据式(3)萤火虫Xi在d维空间向xj移动 12) 计算适应度值f(X),更新荧光亮度 13) FEs=FEs+1 14) End if 15) 利用ULS算子进行局部搜索 16) End for 17) End for 18) 对所有萤火虫排序,确定当前最优位置 19) End while 20) 输出结果 本文采用国际上广泛使用的12个标准测试函数来分析和验证UVFA的收敛速度和解的质量,这12个函数的名称、形式、搜索范围以及最优值如表2所示,其中:函数f1~f7是单峰值函数,f8~f12是具有多个极小值的多峰值函数[18]。Sphere函数为非线性函数,不同维之间可分离,主要用于测试算法的寻优精度;Schwefel2.22函数是具有明显转折点的非线性函数;Schwefel1.2函数的最优解周围具有很小的下降梯度;Schwefel2.21函数为倒锥形非线性函数;Rosenbrock函数为多维病态二次函数,极难进行极小化;Step函数计算一个动态系统的阶跃响应;Quartic with noise函数是凹形非线性函数; Schwefel 2.26函数是具有正弦特点的多个局部极小值的函数;Rastrigin函数使用余弦函数产生局部极小值,是典型多峰函数,域内有大量局部极小点,容易陷入局部最优,而不能得到全局最优解;Ackley函数为连续、旋转、不可分离的多峰函数,具有大量局部最优点;Griewank函数是典型的非线性多模态函数,通常被认为是优化算法很难处理的复杂多模态函数;Penalized1函数使用正弦函数产生大量局部极小值。 实验硬件环境为Intel Core i7-4770 CPU 3.40 GHz处理器,8 GB内存,64位操作系统;软件环境为Windows 7操作系统,Matlab 7.11.0版本。 表2 基准测试函数[18]Tab. 2 Benchmark functions 为了说明UVFA的性能,将其算法参数和对比算法的参数设置成相同的,具体如表3所示。实验中,12个测试函数的维度均设置为30维,每个函数运行30次。 表3 算法参数设置Tab. 3 Algorithm parameters settings 为了客观公正地评价实验结果,采用统计学中的Wilcoxon秩和检验与Friedman检验对实验结果进行分析。Wilcoxon秩和检验基于样本的秩和来判断两个样本是否来自相同的总体,用以分析对比算法的实验结果是否存在显著差异[19]。Friedman检验利用秩分析多个独立样本的总体分布是否存在显著差异,通过对各样本的秩均值进行排名反映算法性能的优劣,秩均值越小表示算法性能越好[20]。 将标准FA、明智步长策略的萤火虫算法(Wise Step Strategy for Firefly Algorithm, WSSFA)[9]、VSSFA、UFA和UVFA运行结果的平均误差值和标准方差进行对比,并给出秩和检验结果,具体数据如表4所示。表中用“-”、“+”和“≈”3个符号分别代表该算法解的质量较UVFA解的质量差、优和相似。带下划线数字表示对比算法中的平均误差最优值。此外,通过对FA、WSSFA、VSSFA与UFA实验数据的秩和检验结果统计显示,在12个测试函数中,UFA全部优于其他3种算法。FA、WSSFA、VSSFA、UFA和UVFA实验结果的Friedman检验秩均值分别为4.54、4.31、3.15、1.85、1.15,进一步说明了UVFA的性能是对比算法中最优的。 针对12个测试函数,UFA的寻优结果都显著地优于标准FA、WSSFA和VSSFA,UVFA较UFA的结果也有了改善。特别是,UFA针对每个函数的平均误差值均比FA、WSSFA和VSSFA有了大幅改进。可见,ULS算子对UVFA的贡献是显著的,可变步长因子在函数f1、f2、f3、f5、f7、f10上的效果较好。 为了更好地反映改进算法的收敛过程,用图2展示了FA、WSSFA、VSSFA、UFA和UVFA对前12个代表函数的收敛曲线并进行对比。图2中横坐标表示函数评价次数,其上界是150 000;纵坐标表示30次实验目标函数均值以10为底的对数形式lg(f)。 由图2可以得出以下结论:第一,改进的局部搜索萤火虫算法的收敛速度明显快于标准萤火虫算法。这种现象是由于ULS算子较强的局部开采能力而产生的,同时可变步长策略又平衡了全局探索能力,故可以提升算法的收敛速度。第二,在进化的初期阶段,UFA与UVFA的收敛速度相当;在进化的后期,UVFA的收敛速度快于UFA。这是合理的。在进化后期,种群中最优解已经陷入局部极值,没有改进空间;与此同时,种群中其他的较优解还存在一定改进的空间,故UVFA的收敛速度会快于UFA,在函数f1、f2、f3、f5、f7、f10上,UVFA算法的求解质量也明显地优于UFA。 表4 算法FA、WSSFA、VSSFA、UFA、UVFA的实验平均误差值(标准方差)对比(30维)Tab. 4 Mean error values (standard deviation) comparison of standard FA, WSSFA,VSSFA, UFA, and UVFA (D=30) 图2 算法FA、WSSFA、VSSFA、UFA、UVFA针对12个测试函数的收敛曲线 Fig. 2 Convergence curves of standard FA, WSSFA,VSSFA, UFA, and UVFA on all test functions 表5是标准FA、WSSFA、VSSFA、UFA和UVFA在12个函数上运行30次所用的平均机器时间数据。可以明显地看出UFA和UVFA在时间上的优势,其理由是ULS算子在搜索过程中对空间的分解和重组需要一定的时间开销,但这个时间与FA搜索过程的时间开销相抵消,并且要小于FA的时间开销。 表5中的平均时间行是每种算法在运行12个测试函数时所耗用的平均时间,速度比是UVFA的平均时间/相应算法的平均时间得到的值,体现了UVFA的速度优势。可以看出,UVFA相对于标准FA、WSSFA和VSSFA的速度比分别是0.31、0.20和0.30,相对于UFA的速度比是0.99,说明了ULS算子在优化过程中对收敛速度的贡献是相当明显的。 通常算法的性能会随着问题规模的增大而降低,为了观察这种影响,表6列出了FA、VSSFA、UFA和UVFA在5维、20维100维等不同维度上的平均误差值和平均标准方差值。带下划线数据表示对比算法中的平均误差最优值,并进行了秩和检验,检验结果的表示同上。每个函数分别独立运行30次。由于10维、50维、200维数据与100维数据结果相似,因此,没有一一列出。 通过对以上5、20和100几种维度的数据进行秩和检验分析,我们发现,UFA在每一种维度上和FA、VSSFA结果相比,均显示出了绝对的优势;UVFA除了具有UFA的优势之外,在低维度问题中,较UFA的优化效果不明显,随着维度的增大,搜索结果显示出普遍的小幅度优化。表7是各算法实验结果的Friedman检验排名,在5维和20维问题中,UFA排名是第一,在100维等其他高维度中UVFA排名第一。从统计学的角度,说明了UVFA在所有参与比较的算法中是最优的。另外,UFA和UVFA的实验时间大幅度降低,在搜索速度上有很大的改进。综合以上结果可见UVFA具有较好的稳定性和鲁棒性,不仅适用于各种低维问题,也适用于复杂的高维问题。 表5五个算法的实验平均机器时间对比s Tab. 5 Experiment average machine time comparison among five algorithms s 表6 各种维度下算法FA、VSSFA、UFA、UVFA的实验平均误差值(标准方差)对比Tab. 6 Mean error values (standard deviation) comparison of standard FA, VSSFA, UFA, and UVFA under various dimensions 表7 各算法实验结果的Friedman检验值Tab. 7 Experimental results of algorithms by Friedman test under different dimensions 以上实验是在U6(66)均匀设计表上进行的,考虑到针对不同规模问题,不同大小的均匀设计表会对实验结果有所影响,因此,设定水平数q=12,独立因素的最大个数k=12,即U12(1212)均匀设计表,以及q=k=18,即U18(1818)均匀设计表,分别在5、20、100三种维度上分别进行UVFA仿真实验,实验结果如表10所示。需要说明的是,如果维数D<因素数k,则只取前D个因素,即均匀设计表中前D列的值进行实验。 从秩和检验的结果可以发现,U12和U18的结果并没有显示出优势,甚至反而使寻优结果变差,验证了文献[13]中关于使用U6(66)进行均匀局部搜索是最合适的选择。 表8 各种维度下不同ULS算子参数对算法UVFA的实验平均误差值对比Tab. 8 Comparison of experimental mean error values with different ULS parameters to UVFA under various dimensions 本文利用ULS算子改进标准FA,提高了萤火虫算法的搜索质量和收敛速度,为了平衡萤火虫全局和局部的搜索能力,特增加可变步长策略,对均匀局部搜索萤火虫算法进一步优化。从实验的结果来看,在不同维度的优化问题中,改进的UVFA的质量均明显地优于标准FA和动态步长萤火虫算法VSSFA,并且实验时间明显缩短,同时,UVFA也显示出较简化版UFA的优越性,证明了改进算法是有效的。 参考文献(References) [1] YANG X S. Nature-Inspired Metaheuristic Algorithms [M]. Beckington, UK: Luniver Press, 2008: 81-96. [2] 徐晓光,胡楠,徐禹翔,等.改进萤火虫算法在路径规划中的应用[J]. 电子测量与仪器学报,2016,30(11):1735-1742.(XU X G, HU N, XU Y X, et al. Application of improved firefly algorithm in path planning [J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(11): 1735-1742.) [3] 李卫军.蛙跳萤火虫算法及其在无线电频谱分配中的应用[J].微型机与应用,2015,34(5):16-18.(LI W J. Study on leapfrog firefly algorithm and its application in the radio spectrum allocation [J]. Microcomputer & Its Applications, 2015, 34(5): 16-18.) [4] 张凯,沈洁.基于萤火虫算法和熵权法的水资源优化配置[J].水资源保护,2016,32(3):50-53.(ZHANG K, SHEN J. Optimal allocation of water resources based on firefly algorithm and entropy method [J]. Water Resources Protection, 2016, 32(3): 50-53.) [5] 王晓新,陈磊.基于高斯过程的萤火虫算法及其在板料成形优化设计中的应用[J].锻压技术,2015,40(12):26-34.(WANG X X, CHEN L. Firefly algorithm and application in sheet metal forming optimization based on Gaussian process [J]. Forging and Stamping Technology, 2015, 40(12): 26-34.) [6] 臧睿,李辉辉.基于标准萤火虫算法的改进与仿真应用[J].计算机科学,2016,43(S2):113-116.(ZANG R, LI H H. Improvement and simulation application based on standard firefly algorithm [J]. Computer Science, 2016, 43(S2): 113-116.) [7] 王翔,于浩杰,颜敏,等.一种新颖的改进萤火虫算法[J].计算机与应用化学,2014(8):987-992.(WANG X, YU H J, YAN M, et al. A novel improved firefly algorithm [J]. Computers and Applied Chemistry, 2014(8): 987-992.) [8] WANG H, CUI Z, SUN H, et al. Randomly attracted firefly algorithm with neighborhood search and dynamic parameter adjustment mechanism [J]. Soft Computing, 2017, 21(18): 5325-5339. [9] YU S, SU S, LU Q, et al. A novel wise step strategy for firefly algorithm [J]. International Journal of Computer Mathematics, 2014, 91(12): 2507-2513. [10] YU S, ZHU S, MA Y, et al. A variable step size firefly algorithm for numerical optimization [J]. Applied Mathematics and Computation, 2015, 263(C): 214-220. [11] 刘金,吴志健,吴双可,等.GPU上的维度并行随机吸引策略萤火虫算法[J].计算机工程与科学,2016,38(10):1961-1966.(LIU J, WU Z J, WU S K, et al. A dimensionally parallel firefly algorithm with random attraction on GPU[J]. Computer Engineering and Science,2016,38(10):1961-1966.) [12] 陆克中,孙俊.全局信息共享的自适应FA算法[J].计算机工程与科学,2016,38(6):1164-1170.(LU K Z, SUN J. An adaptive FA algorithm based on global information sharing [J]. Computer Engineering and Science, 2016, 38(6): 1164-1170.) [13] PENG H, WU Z J, DENG C S. Enhancing differential evolution with commensal learning and uniform local search [J]. Chinese Journal of Electronics, 2017, 26(4): 725-733. [14] YANG X S. Firefly algorithm, stochastic test functions and design optimisation [J]. International Journal of Bio-Inspired Computation, 2010, 2(2): 78-84. [15] WANG Y, FANG K T. A note on uniform distribution and experimental design [J]. Science Bulletin, 1981, 26(6): 485-489. [16] 王元.均匀设计──一种试验设计方法[J].科技导报,1994,12(5):20-21.(WANG Y. Uniform design ─ a method for experimental design [J]. Science and Technology Review, 1994, 12(5): 20-21.) [17] FANG K T, MA C, WINKER P, et al. Uniform design: theory and application [J]. Technometrics, 2000, 42(3): 237-248. [18] YAO X, LIU Y, LIN G. Evolutionary programming made faster [J]. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. [19] ROSNER B, GLYNN R J, LEE M L T. Incorporation of clustering effects for the Wilcoxon rank sum test: a large-sample approach [J]. Biometrics, 2003, 59(4): 1089-1098. [20] FRIEDMAN M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance [J]. Journal of the American Statistical Association, 1937, 32(200): 675-701. This work is partially supported by the National Natural Science Foundation of China (61364025, 61763019), the Science and Technology Project of Jiangxi Provincial Education Department (GJJ161072, GJJ161076). WANGXiaojing, born in 1980, M. S., lecturer. Her research interests include evolutionary computation. PENGHu, born in 1981, Ph. D., lecturer. His research interests include evolutionary computation. DENGChangshou, born in 1972, Ph. D., professor. His research interests include intelligent computing, data mining. HUANGHaiyan, born in 1982, M. S., lecturer. Her research interests include evolutionary computation. ZHANGYan, born in 1979, M. S., lecturer. Her research interests include evolutionary computation. TANXujie, born in 1978, M. S., lecturer. His research interests include intelligent computing.2 改进的萤火虫算法
2.1 均匀局部搜索
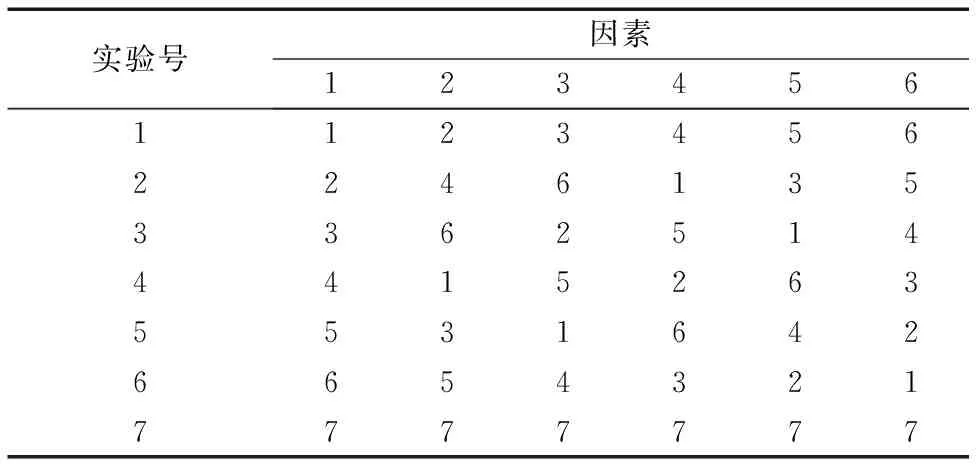
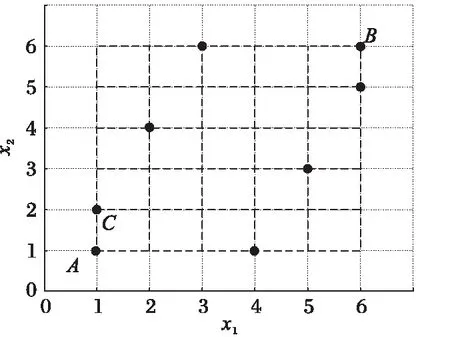
2.2 基于均匀局部搜索和可变步长策略的萤火虫优化算法
3 实验仿真及分析
3.1 测试函数及算法参数设置


3.2 实验结果及算法收敛性对比分析
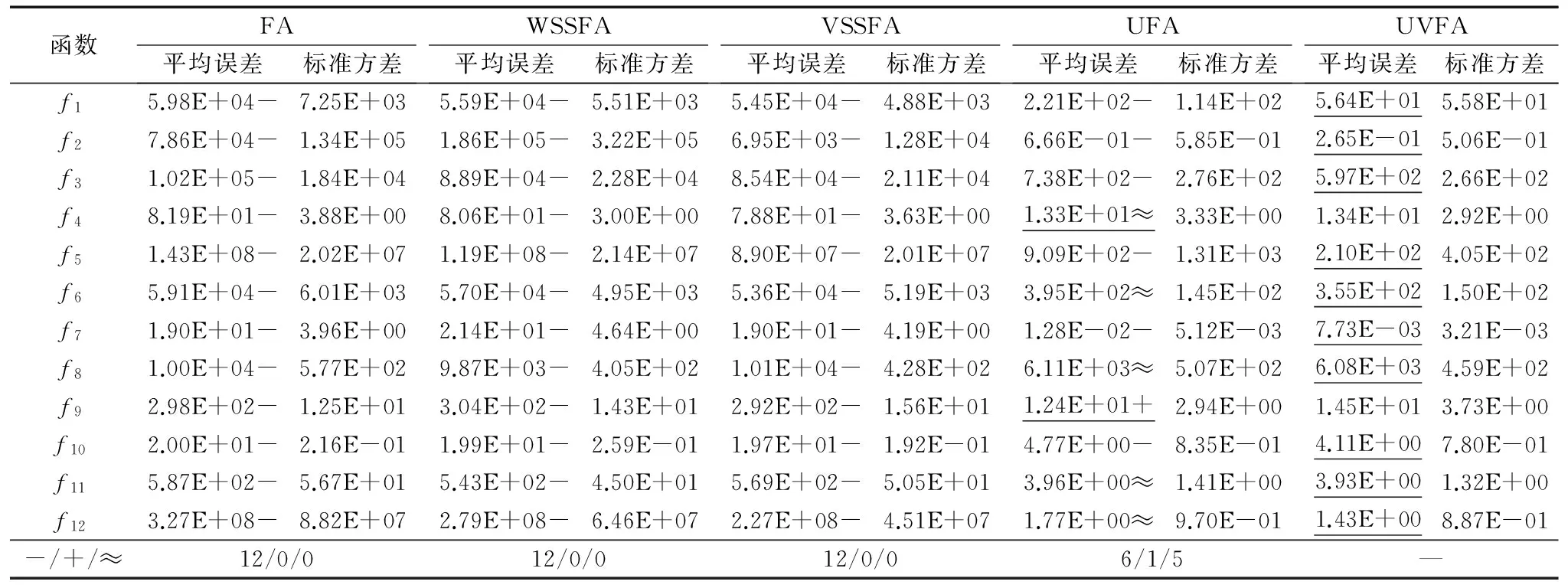
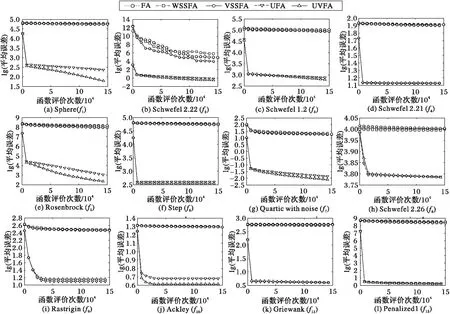
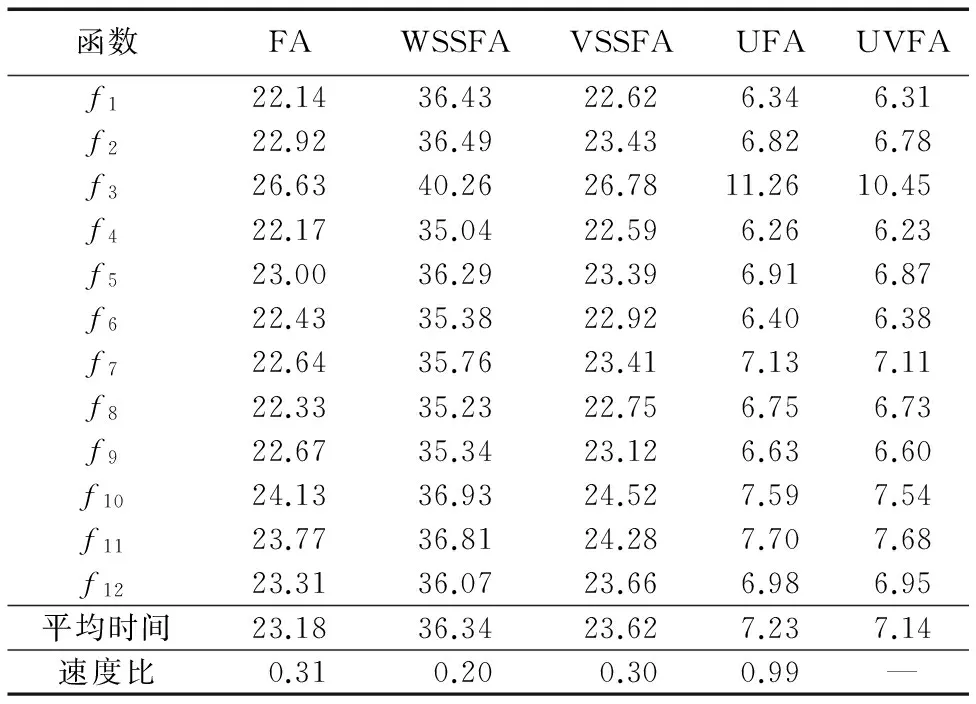
3.3 时间开销分析
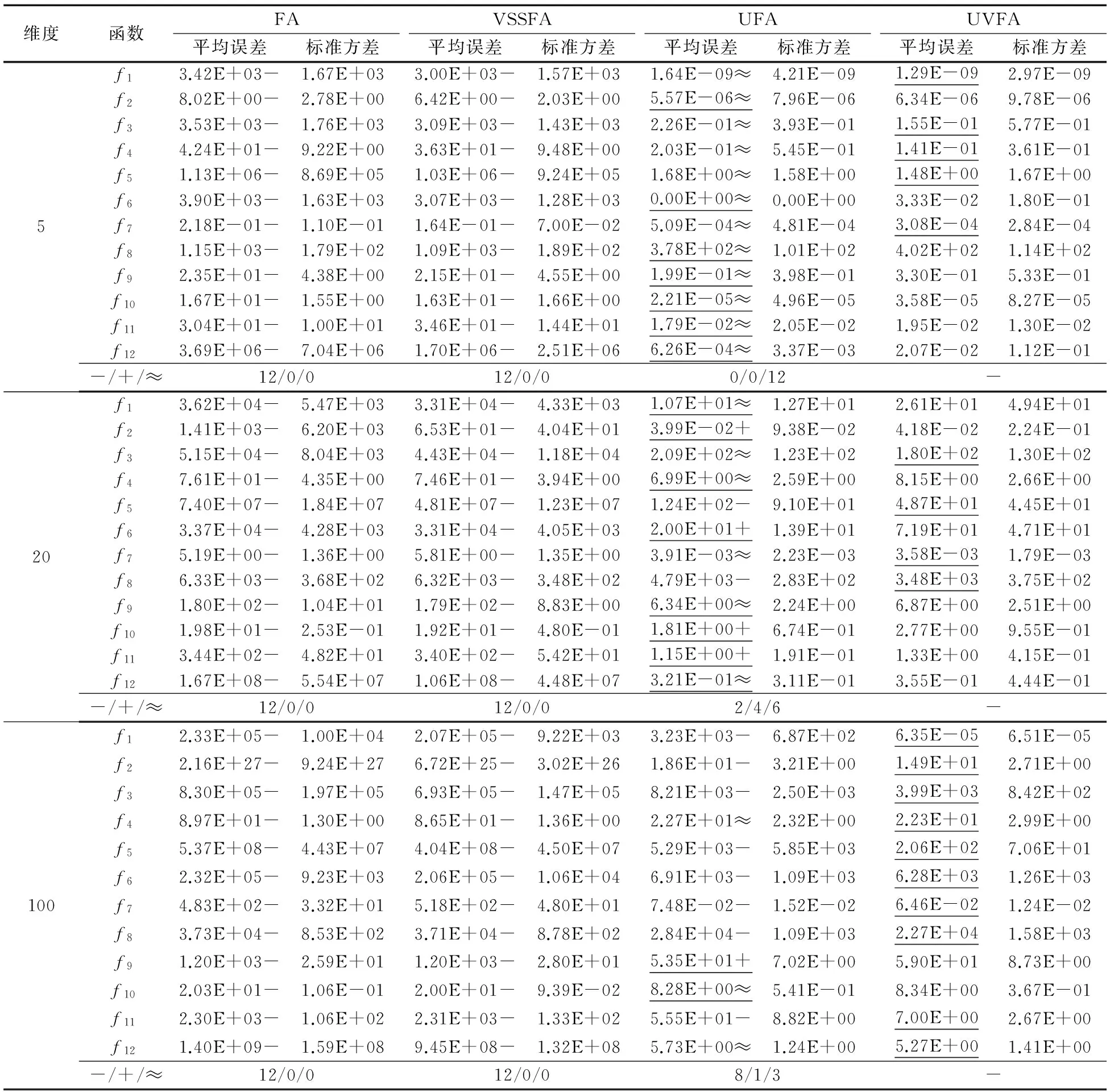
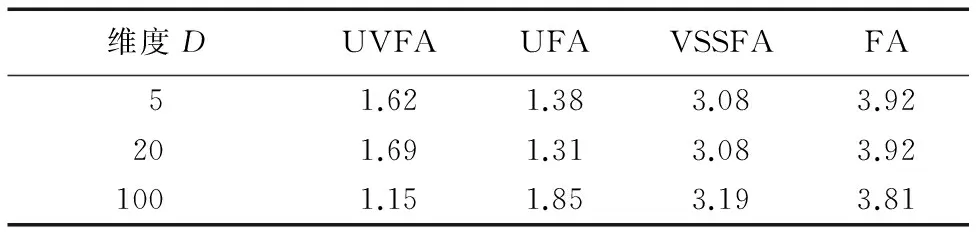
3.4 维数变化分析
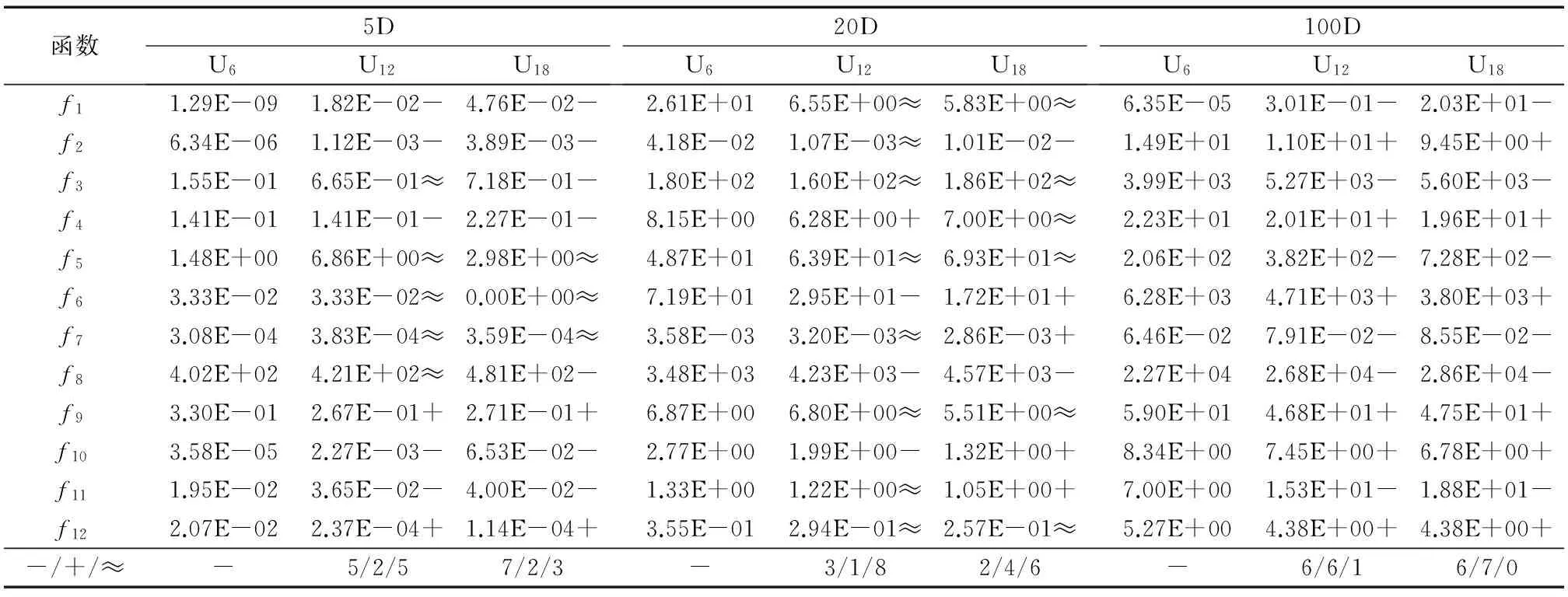
3.5 ULS算子参数变化对UVFA的影响分析
4 结语

