基于动态遗忘因子递推最小二乘算法的船舶航向模型辨识
孙功武,谢基榕,王俊轩
(中国船舶科学研究中心 深海载人装备国家重点实验室,江苏 无锡 214082)
0 引言
船舶是一个典型的时变系统,其模型参数会随航行环境和工况的变化而变化。采用辨识方法获取船舶航行过程中不确定的模型参数,可以为船舶的特性研究和控制策略设计奠定重要基础。传统的参数辨识方法主要有极大似然法、递推最小二乘(Recursive Least Squares, RLS )算法、卡尔曼滤波法等[1-5]。其中,RLS算法的计算量小,且不需要估计变量的任何统计特性,应用非常广泛。文献[3]将RLS算法应用在电机电感、电阻等参数的辨识中,然后通过实验验证了该算法的准确性和实时性,非常适用于参数的在线辨识。文献[4]采用RLS算法在线辨识水下机器人的模型参数,并根据辨识结果修正控制器参数,以提高机器人的控制效果。为改善RLS算法的性能,文献[6]提出了一种能同时获得较高辨识精度和收敛速度的变遗忘因子RLS算法,由于该算法仅根据当前的残差对遗忘因子进行在线调整,导致调整量计算易受到噪声干扰的影响。经过多年的研究发展,还出现了广义最小二乘法、正交最小二乘法、偏最小二乘法等改进算法[7-9],使参数辨识的适用领域得到进一步拓展,然而这类算法对噪声的鲁棒性不强,难以在复杂非线性系统中获得高精度的辨识效果。近年来,智能算法的发展为参数辨识提供了新的途径。文献[10]将建筑物热模型的参数辨识问题转化为参数最优化问题,然后采用进化算法对模型参数进行寻优,利用该算法优越的全局搜索能力和对噪声的强鲁棒性实现了模型参数的高精度求解,但进化算法实现的复杂度要远大于RLS算法。与进化算法辨识模型参数的步骤类似,很多学者将粒子群算法、蚁群算法、遗传算法等[11-14]应用于多个领域系统模型的参数辨识,并都取得了高精度的辨识结果,但同样存在算法计算量大的问题。对于文献[10-14]中采用优化算法辨识模型参数的问题,搜索空间范围对算法的收敛速度和精度都有直接的影响。为获取最佳的搜索空间,文献[15]先利用RLS算法初步辨识模型参数,然后在初步辨识结果的附近小范围内采用差分进化算法进行寻优,从而大幅度提高了参数辨识的精度,但辨识过程的复杂度也增加了。此外,采用神经网络、支持向量机等学习算法[16-18]也可以准确地辨识出模型参数。文献[10-18]中提出的智能算法适用于简单的线性、复杂的多变量非线性等各种系统的参数辨识,并具有很高的辨识精度,但辨识过程需要进行多次的迭代计算或训练,算法复杂、计算耗时长、对处理器性能的要求高,限制了实际的应用范围。
考虑到船舶航向数学模型为单输入单输出的线性模型,非常适合采用遗忘因子RLS算法对模型参数进行在线辨识,并针对恒定遗忘因子不能使算法同时具备优越的跟踪性能及收敛精度的问题,提出一种基于模糊控制的遗忘因子在线修正方法,最后通过仿真对该方法的有效性进行了验证。
1 船舶航向模型及遗忘因子RLS算法
航向保持是船舶最常用的一种航行工况,该工况下通过给定小舵角来控制船舶航向。此时,船舶的航向数学模型可以采用一阶Nomoto线性模型[19]表示为:
(1)
其中:ψ为航向角;δ为舵角;K、T是与船体结构尺寸、载重、航速、吃水等因素相关的参数。式(1)表明,在不同航速、不同载重等情况下,船舶航向模型中的参数也不相同。采用双线性变换法可以将式(1)离散化为:
ψ(k)+a1ψ(k-1)+a2ψ(k-2)=b1δ(k)+
b2δ(k-1)+b3δ(k-2)
(2)
RLS算法是目前应用最广泛的参数在线辨识算法之一,采用该算法辨识船舶航向模型参数的迭代计算公式为:
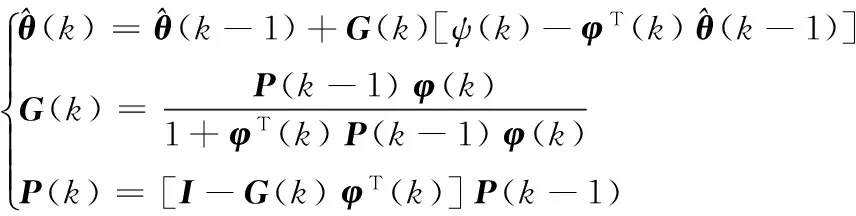
(3)
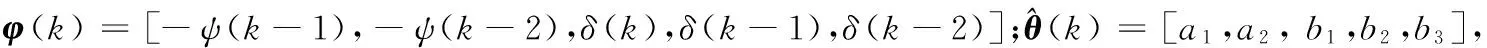
RLS算法在计算中将所有的数据同等对待,随着算法迭代次数的增加,会出现“数据饱和”现象,降低算法的收敛速度。为减小历史数据对当前参数辨识结果的影响,可以通过为每个数据增加一个权值来改进算法,形成遗忘因子RLS算法。引入遗忘因子后,船舶航向模型参数辨识的迭代计算公式被修正为:
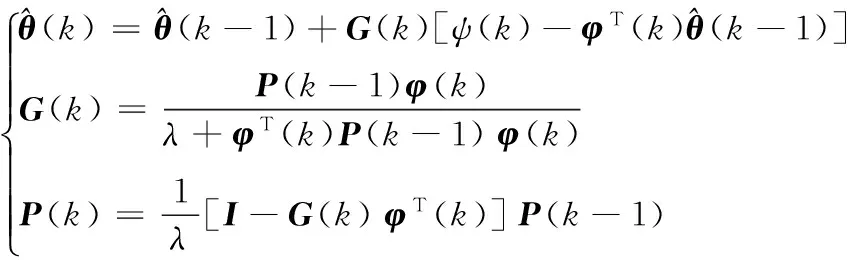
(4)
其中λ为遗忘因子。
在对系统的输入输出采样过程中会混入均值为0的随机噪声干扰,噪声干扰越大,系统参数的辨识精度也会越低。在RLS算法中引入遗忘因子λ,能够改善算法的跟踪性能,但也在一定程度上降低了算法对噪声的鲁棒性。遗忘因子RLS算法的性能在很大程度上取决于λ的大小,当λ较小时,算法的收敛速度较快,但对噪声会较敏感,导致算法收敛时的参数辨识精度较低;当选取较大的λ时,能够提高算法对噪声的鲁棒性,但削弱了其跟踪能力。因此,设计遗忘因子RLS算法时,λ值的取值非常重要,需要综合考虑算法的收敛速度和对噪声的鲁棒性进行折中选取。
2 基于模糊控制的动态遗忘因子RLS算法
2.1 动态遗忘因子设计思想
在常规的遗忘因子RLS算法中,λ为恒定值,根据算法的跟踪性能和对噪声的鲁棒性来折中确定λ值会导致算法的两种性能都有一定的“牺牲”。若能够在辨识过程中实时评估辨识结果与实际模型参数之间的接近程度,并根据接近程度对遗忘因子进行动态调整则可大幅度提高算法的综合性能。由于实际模型的参数未知,无法直接计算参数辨识的误差,所以只能通过其他途径对误差进行评估。
计k时刻的理论模型输出与实际模型输出之间的残差为:
(5)
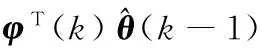
残差主要是由噪声干扰和参数辨识误差引起的,其中的噪声干扰对残差的影响很小。当参数辨识的误差较大时,残差绝对值也较大,此时希望遗忘因子的值较小,使RLS算法的辨识结果能够快速收敛到实际模型参数附近;随着算法的执行,参数辨识的误差越来越小,残差绝对值不断减小,此时希望遗忘因子能适当增大,以抑制噪声对辨识精度的影响。可见,通过残差可以间接评估参数辨识误差的大小。
2.2 基于模糊控制的遗忘因子在线修正
在遗忘因子的修正过程中,仅根据单次残差绝对值修正遗忘因子,会使修正过程对噪声比较敏感。为此,可以取一段时间内残差绝对值的平均值作为辨识参数与实际参数接近程度的评价函数,再将评价函数作为修正遗忘因子的参考依据。第k时刻,评价函数J的计算为:
(6)
其中n为选取残差的数量。
通过分析可知,遗忘因子的期望修正量应该与评价函数呈反相关关系,但难以建立两者之间的精确表达式。因此,本文引入模糊理论,设计模糊控制器对遗忘因子进行在线修正,并将评价函数作为模糊控制器的一个输入。同时,鉴于评价函数的变化率ΔJ可以反映辨识误差的变化趋势,将ΔJ也作为模糊控制器的一个输入。第k时刻,ΔJ的计算如下:
(7)
其中m为计算变化率的时间常数的离散值。
设计基于模糊控制的遗忘因子在线修正原理如图1所示。
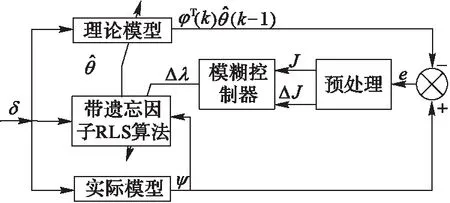
图1 基于模糊控制的遗忘因子在线修正 Fig. 1 Online correction of forgetting factor based on fuzzy control
图1中,预处理部分根据式(6)和式(7)对残差进行处理得到J和ΔJ,模糊控制器根据输入J和ΔJ实时计算修正量Δλ,将遗忘因子的修正为:
λ=λ0+Δλ
(8)
其中λ0是遗忘因子的初值。
采用动态遗忘因子RLS算法进行模型参数辨识时,模型参数的辨识计算在每个采样周期会执行一次。为在一定程度上减小算法的计算量,遗忘因子的修正周期可以取采样周期的l倍。辨识算法在程序实现时,首先定义并初始化变量nc=0,然后在每个采样周期到达时,执行如下步骤:
步骤1 令nc=nc+1,采样实际模型的输入和输出,并根据式(5)计算残差。
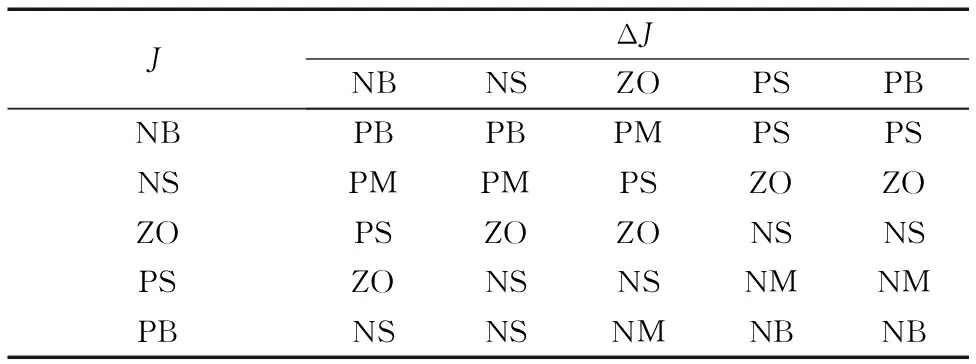
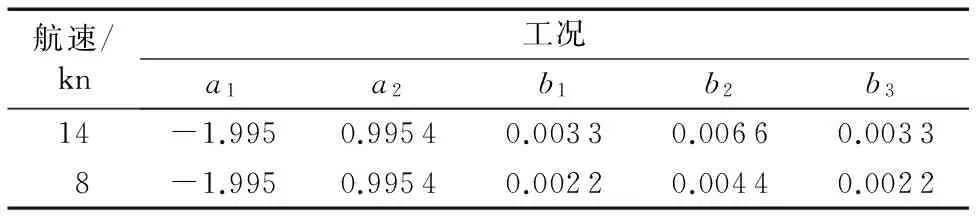
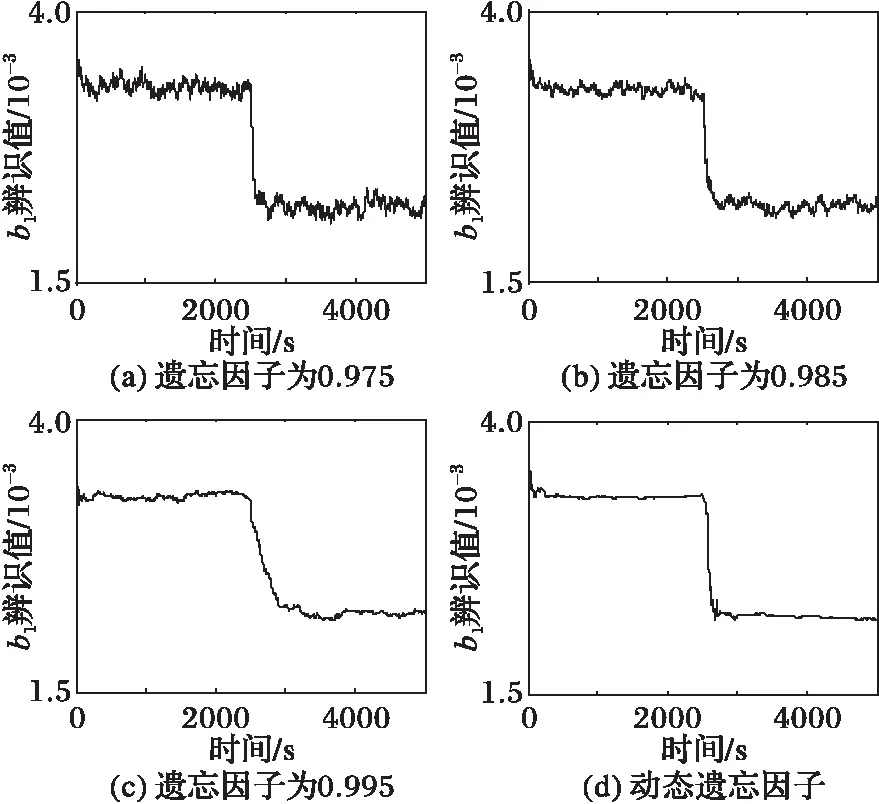
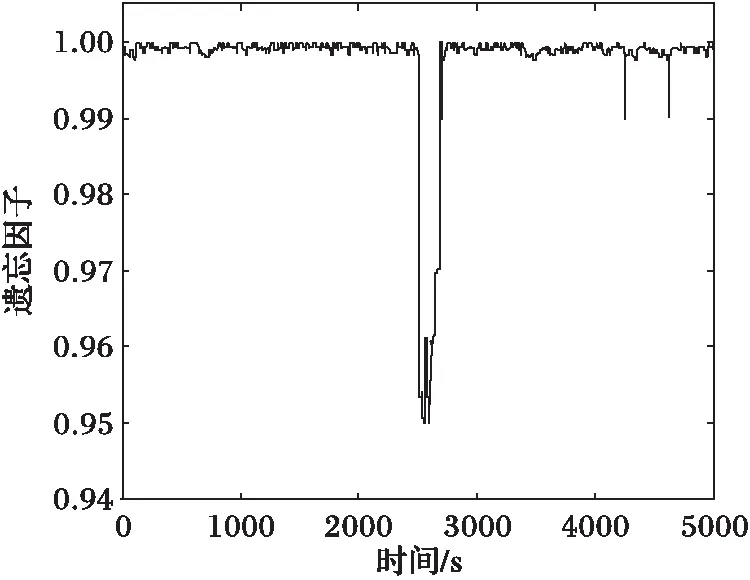
步骤2 如果nc 步骤2.1 根据式(6)和式(7)对残差进行预处理,得到J和ΔJ。 步骤2.2 将J和ΔJ作为模糊控制器的输入,利用模糊控制器推理计算Δλ。 步骤2.3 根据式(8)修正此时的遗忘因子λ,将修正后的λ代入式(4)中,完成一次遗忘因子的更新。 循环执行上述过程,便实现模型参数的在线辨识。 模糊控制器设计时,首先通过线性变换将输入输出的精确量映射到模糊论域,取输入J和ΔJ模糊论域都为[-2,2],取输出Δλ的模糊论域为[-3,3]。选择J和ΔJ对应模糊语言集为{NB(正大),NS(负小),ZO(零),PS(正小),PB(正大)},取输出Δλ对应模糊语言集为{ NB(正大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}。采用三角形函数设计控制器输入输出的隶属函数。 模糊控制规则表是模糊控制器设计的核心,当J和ΔJ都为正大时,表明辨识参数有大的误差,且误差还在迅速增大,此时期望模糊控制器输出的Δλ为负大,将遗忘因子修正为极小值,使算法具有快速跟踪的能力;当J为正大且ΔJ负大时,表明辨识参数有大误差,但误差还在迅速减小,此时输出Δλ为负小;当J和ΔJ都为负大时,表明辨识参数已经非常接近实际参数,且误差还在迅速减小,此时期望输出的Δλ为正大,将遗忘因子修正为极大值,使算法具备高辨识精度;当J为负大且ΔJ为正大,期望模糊控制器输出的Δλ为正小。根据上述原则,制定5×5的模糊控制规则表如表1所示。 根据表1的模糊规则表,采用Mamdani模糊推理和重心法计算输出Δλ。 表1 模糊控制规则表ΔλTab. 1 Fuzzy control rule table Δλ 以小舵角控制工况下的某工程船为研究对象,该船总长82.7 m,型宽14.2 m,型深7.8 m,排水4 600 t,其离散化的数学模型同式(2)。假设船舶初始航速为14 kn,在2 500 s时切换到8 kn航行,采样周期取1 s,两种航速下的船舶模型参数如表2所示。 表2 不同航速下的船舶模型参数Tab. 2 Ship model parameters with different speed 采用本文方法对上述航行过程中的模型参数进行在线辨识仿真。算法中m=100,n=15,l=10,λ0=0.975,在模型输入端施加0.1 Hz的三角波信号模拟输入舵角值,在模型输出端叠加高斯白噪声模拟实际采样到的航向角。船舶实际航速调节需要较长的过渡时间,而考虑到模型参数变化缓慢难以使辨识算法收敛的快速性得到较好的对比验证,因此在仿真中人为设置模型参数b1、b2和b3在第2 500 s发生突变。将本文算法对模型参数b1、b2和b3的辨识结果与恒定遗忘因子RLS算法的辨识结果进行对比,结果分别如图2、图3和图4所示。 图2 b1辨识结果 Fig. 2 Identification results of b1 图2、图3和图4的仿真结果表明:恒定遗忘因子RLS算法中的遗忘因子越大,算法辨识的稳态精度越高,但对模型参数突变时的跟踪能力变差,收敛速度变慢;而本文所提的动态遗忘因子RLS算法不仅在模型参数平稳时有很高的辨识精度,在模型参数突变时也能迅速跟踪参数的变化。 图3 b2辨识结果 Fig. 3 Identification results of b2 图4 b3辨识结果 Fig. 4 Identification results of b3 在整个航行过程中,船舶模型参数a1和a2保持不变,辨识结果分别如图5和图6所示。 图5和图6图中,本文方法对参数a1和a2的辨识结果在第2 500 s开始出现短时间的波动,但在其他时间段内都有非常高的辨识精度,综合整个过程的辨识效果仍具有一定的优势。 基于模糊控制的动态遗忘因子RLS算法在整个参数辨识过程中,遗忘因子的调整如图7所示。 图7中,遗忘因子的动态变化曲线充分解释了图2(d)至图6(d)辨识结果,当模型参数平稳时,遗忘因子被修正为较大值,此时算法对噪声的鲁棒性较强,辨识精度较高;当模型参数在第2 500 s出现突变时,遗忘因子被迅速修正为较小值,使算法的收敛速度较快,如图2(d)至图4(d)所示。在遗忘因子较小的时间段内,算法也会对噪声比较敏感,因此出现图5(d)和图6(d)中第2 500 s开始出现的短期波动。 本文在评价函数及其变化率计算中引入了参数m和n,以减小噪声干扰对遗忘因子调整的影响,但也会造成遗忘因子期望的修正滞后于实际模型参数的变化,使模型参数在2 500 s发生突变时,遗忘因子没有立即被修正为最小值,如图7所示。同时,结合图2(d)、3(d)、4(d)和图7可以得出,在辨识算法收敛到真实模型参数值附近时,遗忘因子也没有立即被修正为最大值。遗忘因子修正的滞后,会导致算法在模型参数突变初期的跟踪速度不会达到最快,在算法初次收敛到模型参数真实值附近后仍会持续小幅度波动一段时间。 图5 a1辨识结果 Fig. 5 Identification results of a1 图6 a2辨识结果 Fig. 6 Identification results of a2 图7 遗忘因子的调整过程 Fig. 7 Adjustment process of forgetting factor 提出了一种基于模糊控制的动态遗忘因子RLS算法,并采用该算法对小舵角控制工况下的船舶航向运动模型参数进行辨识仿真。仿真结果表明,该算法中的遗忘因子能够根据参数辨识误差进行实时修正,使算法同时具备优越的辨识精度和收敛速度。所提算法将构造的评价函数及其变化率作为遗忘因子调整的依据,并采用模糊控制器实现遗忘因子修正量的计算,使算法的应用不依赖于被辨识对象的具体领域,且改进后的算法仍具有较小的计算量,其实现过程简单、实时性强、通用性好,具有较高的应用价值。 本文仅对单输入输出系统模型参数进行了辨识研究,若要所提算法推广应用在多输入输出系统的参数辨识中,则需要对评价函数进行适当的改造。同时,如何获取参数m、n、l的最佳值需要进一步探讨。 参考文献(References) [1] REYNDERS E. System identification methods for (operational) modal analysis: review and comparison [J]. Archives of Computational Methods in Engineering, 2012, 19(1): 51-124. [2] 衷路生,李兵,龚锦红,等.高速列车非线性模型的极大似然辨识[J].自动化学报,2014,40(12):2950-2958.(ZHONG L S,LI B,GONG J H, et al. Maximum likelihood identification of nonlinear model for high-speed train [J]. Acta Automatica Sinica,2014, 40(12): 2950-2958.) [3] ZHANG H, GONG S J, DONG Z Z. On-line parameter identification of induction motor based on RLS algorithm [C]// Proceedings of the 2013 International Conference on Electrical Machines and Systems. Piscataway, NJ: IEEE, 2013: 2132-2137. [4] 刘慧婷,冯金金,张明.水下机器人操纵系统优化控制研究[J].计算机仿真, 2016,33(5):299-303.(LIU H T, FENG J J, ZHANG M. Research on optimal control of underwater robot control system [J]. Computer Simulation, 2016, 33(5): 299-303.) [5] 石刚,赵伟,刘珊珊.基于无迹卡尔曼滤波估算电池SOC[J].计算机应用,2016,36(12):3492-3498.(SHI G, ZHAO W, LIU S S. Battery SOC estimation based on unscented Kalman filtering [J]. Journal of Computer Applications, 2016,36(12):3492-3498.) [6] 陈涵,刘会金,李大路,等.可变遗忘因子递推最小二乘法对时变参数测量[J].高电压技术,2008,34(7):1474-1477.(CHEN H, LIU H J, LI D L, et al. Time-varying parameters measurement by least square method with variable forgetting factors [J]. High Voltage Engineering, 2008, 34(7):1474-1477.) [7] SALEHI R, DEHGHAN M. A generalized moving least square reproducing kernel method [J]. Journal of Computational & Applied Mathematics, 2013, 249(6):120-132. [8] CHEN C, LI Y. An orthogonal least-square-based method for DEM generalization [J]. International Journal of Geographical Information Science, 2013, 27(1): 154-167. [9] 何开锋,钱炜祺,张勇,等.偏最小二乘法在气动数据建模中的应用[J].宇航学报,2014,35(3):277-282.(HE K F, QIAN W Q, ZHANG Y, et al. Application of partial least squares regression method in modeling of aerodynamic data [J]. Journal of Astronautics, 2014, 35(3): 277-282.) [10] YANG Z, LI X, BOWERS C P, et al. An efficient evolutionary approach to parameter identification in a building thermal model [J]. IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews, 2012,42(6):957-969. [11] 张来福,田赟,姜敏,等.基于遗传算法的伺服系统摩擦参数辨识与仿真[J].计算机应用,2016,36(S1):110-112.(ZHANG L F, TIAN Y, JIANG M, et al. Friction parameter identification and simulation of servo system based on genetic algorithm [J]. Journal of Computer Applications, 2016,36(S1):110-112.) [12] 孙黎霞,倪瑶,马骙军.混沌遗传算法在励磁系统参数辨识中的应用[J].电气技术,2012(9):9-14.(SUN L X, NI Y, MA K J. Study on parameter identification of excitation system based on chaos genetic algorithm [J]. Electrical Engineering, 2012, (9):9-14.) [13] ALFI A, MODARES H. System identification and control using adaptive particle swarm optimization [J]. Applied Mathematical Modelling, 2011, 35(3):1210-1221. [14] YANG S, WU M, YAO X, et al. Load modeling and identification based on ant colony algorithms for EV charging stations [J]. IEEE Transactions on Power Systems, 2014, 30(4):1997-2003. [15] 魏彤,田双彪.基于RLS-DE算法的多变量径向磁轴承系统辨识[J].机械工程学报,2016,52(3):143-150.(WEI T, TIAN S B. The identification of multivariable radial magnetic bearing system based on RLS-DE algorithm [J]. Journal of Mechanical Engineering , 2016,52(3):143-150.) [16] 王兵,李盼池,许少华.一种基于过程神经元网络辨识的PID控制模型及方法[J].计算机应用,2010,30(1):233-235.(WANG B , LI P C, XU S H. PID control model and method based on process neural network identification [J]. Journal of Computer Applications, 2010, 30(1): 233-235.) [17] ZHAO H, GAO S, HE Z, et al. Identification of nonlinear dynamic system using a novel recurrent wavelet neural network based on the pipelined architecture [J]. IEEE Transactions on Industrial Electronics, 2014, 61(8):4171-4182. [18] AL-DHAIFLLAH M, WESTWICK D T. Identification of auto-regressive exogenous hammerstein models based on support vector machine regression [J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2083-2090. [19] BANAZADEH A, GHORBANI M T. Frequency domain identification of the Nomoto model to facilitate Kalman filter estimation and PID heading control of a patrol vessel [J]. Ocean Engineering, 2013, 72(4): 344-355. This work is partially supported by the Natural Science Foundation of Jiangsu Province (BK20170217). SUNGongwu, born in 1990, M. S., engineer. His research interests include intelligent control of ship, system identification. XIEJirong, born in 1977, Ph. D., research fellow. His research interests include intelligent control of ship, integrated information system. WANGJunxuan, born in 1986, M. S., senior engineer. His research interests include intelligent control of ship, integrated information system.2.3 模糊控制器设计
3 仿真研究
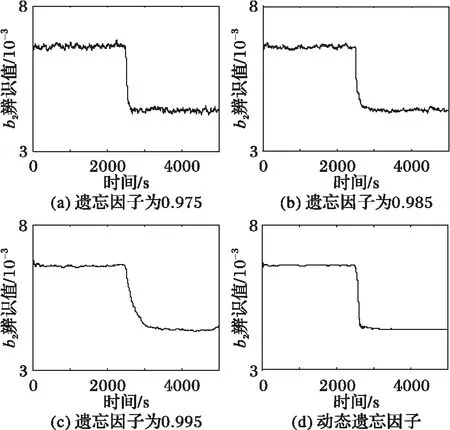
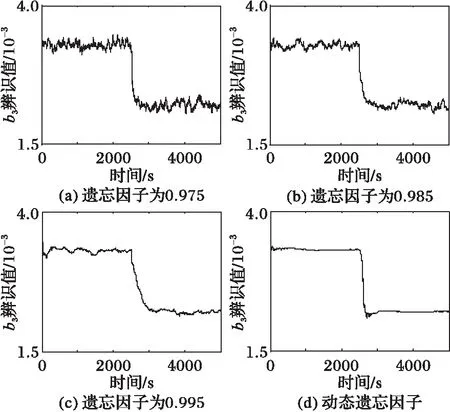
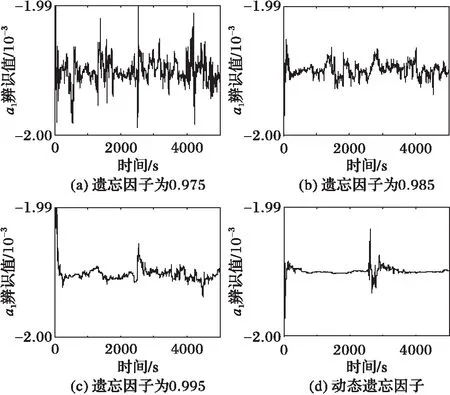
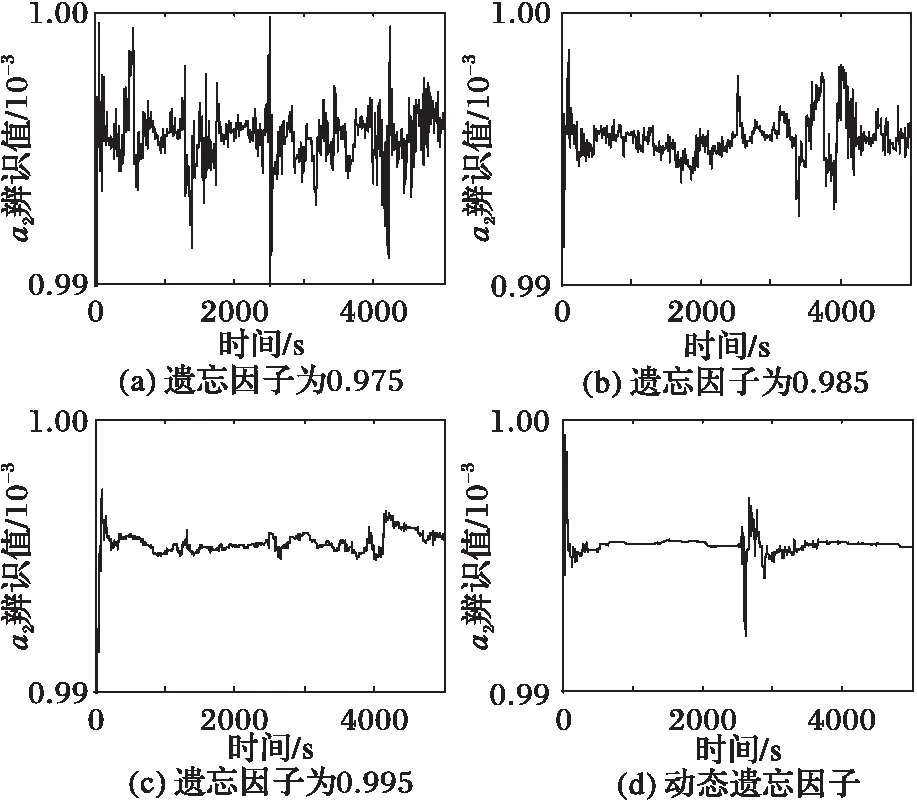
4 结语

