AdaBoost的多样性分析及改进
王玲娣,徐 华
(江南大学 物联网工程学院,江苏 无锡 214122)
0 引言
集成学习是当前机器学习的热点研究方向之一,和传统单个分类器的构造目的不同,它并非力求得到单一最优分类器,而是按照一定策略集成一组个体分类器。在两种经典的集成算法:Boosting[1]和Bagging[2]被提出之后,研究者又陆续提出了大量的集成学习算法。其中Boosting算法可将粗糙的、不太正确的、简单的初级预测方法,按照一定的规则构造出一个复杂的,精确度很高的预测方法,但是很难运用于实际中;AdaBoost[3]的出现有效地解决了这一问题,因此AdaBoost成为了Boosting家族的代表算法,受到极大的关注,成功应用于声音文件检索[4]、人脸识别[5]、癌症诊断[6]及目标检测[7-8]等实际问题中。
集成学习主要有两个阶段:一是基分类器的生成;二是组合策略的选择。将相同的基分类器进行集成是无意义的,因为组合而成的分类器与基分类器的分类结果必然相同。所以基分类器之间要存在差异,即分类器多样性。Krogh等[9]证明,集成的泛化误差是由个体分类器的平均泛化误差和平均差异度决定的。虽然目前已存在多种多样性度量方式,但是关于它的严格定义并不统一[10-11],只是可以从大量研究资料中获知,多样性有益于集成方法的设计,如:2012年,文献[12]使用遗传算法组合不同的多样性用于选择性集成;而文献[13]于2014年通过向量空间模型形象地论证了多样性的有效性;2015年文献[14]明确提到多样性是集成学习成功的重要条件;文献[15]在2016年研究了很可能接近正确的(Probably Approximately Correct, PAC)学习框架下多样性对基于投票组合策略的集成方法泛化能力的影响。多样性对于AdaBoost来说同样重要,文献[16]提出一种基于随机子空间和AdaBoost自适应集成方法,将随机子空间融合到AdaBoost的训练过程中,目的就是增加AdaBoost的多样性。文献[17]详细总结了AdaBoost的发展,并指出它的进一步研究方向之一是其弱分类器的多样性研究,因为有关分类器多样性的研究,有效结论太少,有待深入与完善。也有文献[18]研究了多样性度量在AdaBoost.M2算法下的变化,得到一些规律,但如何使用这些规律以及最终能否提高集成性能,并没给出答案。
针对上述问题,本文研究了4种成对型多样性度量在AdaBoost算法下的变化;并利用皮尔逊相关系数定量分析多样性度量和分类性能之间的关系,发现双误度量(Double Fault, DF)变化模式固定——先增加后平缓;进一步,提出了一种基于DF改进的AdaBoost算法。结果表明改进后的算法可以抑制AdaBoost的过适应现象,降低错误率。
1 成对型多样性度量
关于成对多样性的研究主要集中在以下3个方面:1)多样性的度量方法;2)多样性度量与集成学习精度的关系;3)如何利用多样性度量更好地选择分类器来构建集成系统,以提高集成学习的性能。本文按照上述思路,先介绍4个成对型多样性度量方法,然后研究这四种多样性度量与AdaBoost产生的分类器精度有怎样的关系,最后利用DF改进AdaBoost算法。
成对型多样性度量是定义在两个分类器上的,假设分类器集合H={h1,h2,…,hm},hi和hj(i≠j)为两个不同的分类器,它们对同一组样本分类情况组合如表1所示,其中样本总数为n。表1中,n11(n00) 代表被hi和hj共同正确(错误)分类的样本数,n10代表被hi正确分类、hj错误分类的样本数,n01代表被hi错误分类、hj正确分类的样本数,并且它们满足式(1):
n11+n00+n10+n01=n
(1)
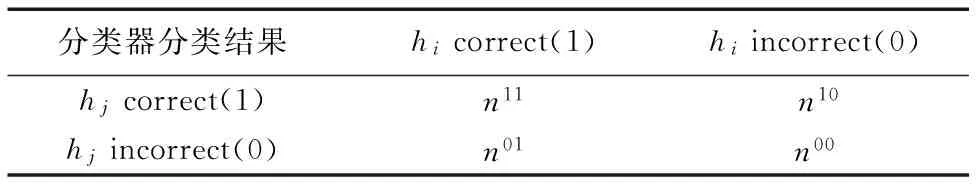
表1 两个分类器的分类结果组合Tab. 1 Result combination of two classifiers
下面将分别介绍4种成对型多样性度量。
1)Q统计。
Q统计(Q-statistics, Q)[19]源于统计学,它的计算公式如下:
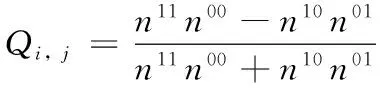
(2)
由式(2)可知Q的取值范围是[-1,1]。当两个分类器的分类结果趋于一致时,Q值为正,否则为负,完全相同时为1,完全不同时为-1。
2)相关系数。
相关系数(Correlation coefficient,ρ)[20]源于统计学,ρ的取值范围为[-1,1],计算公式如下:
(3)
3)不一致度量。
不一致度量(Disagreement Measure, DM)[21]衡量的是两个分类器分类结果不一致的程度,它的值越大,表明两个分类器的多样性越大,取值范围为[0,1],计算公式如下所示:
DMi, j=(n10+n01)/n
(4)
4)双误度量。
双误度量(DF)[22]关注的是两个分类器在相同样本上出错的情况,取值范围[0,1],最差的情况是两个分类器错误率都是100%,此时DF的值为1,分类器的正确性与多样性同时降到最低。计算公式如下:
DFi, j=n00/n
(5)

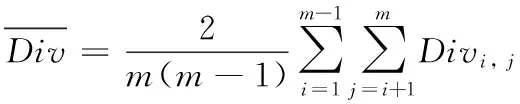
(6)
2 AdaBoost算法
2.1 算法描述
能否使用多个弱分类器来构建一个强分类器?这是一个有趣的理论问题。“弱”意味着分类器的性能仅仅比随机猜测略好,而“强”则表明分类器表现不错。AdaBoost即脱胎于上述理论问题。AdaBoost算法是一个迭代过程,原理是:算法运行过程中会给训练样本赋予权重,一开始,初始化成相等值,然后根据弱分类器学习算法训练第一个弱分类器,接着根据该分类器的加权误差更新样本权重,降低被正确分类的样本权重,提高被错误分类的样本权重。基于新的样本权重分布,继续训练弱分类器。如此往复,便可得到一组弱分类器,每个弱分类器也有一个权重,代表它在最后集成中的重要性。
下面将具体介绍样本权重的更新过程。
对于二分类问题,令S={(xi,yi)|i=1,2,…,n}表示训练样本集,其中yi∈{-1,1}代表样本标签。Dt表示第t轮迭代的样本分布矢量,初始化时,D1={1/n,1/n,…,1/n}。在AdaBoost算法中,基分类器ht的重要性和它在样本权重分布上的错误率εt相关,也被称为加权误差,定义如下:
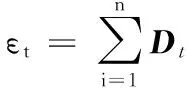
(7)
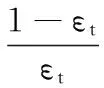
(8)
接下来,根据αt来更新样本(xi,yi)权重,见式(9):
Dt+1(i)=(Dt(i)exp(-yiht(xi)αt))/Zt
(9)
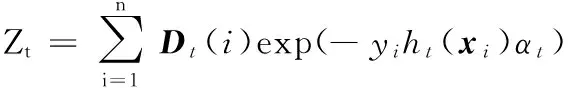
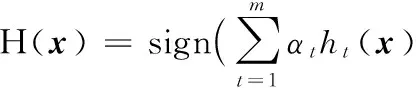
(10)
2.2 算法问题分析
由上述可知,在AdaBoost的训练过程中,分类器的重心将被转移到比较难分类的样本上,这也是AdaBoost可以将“弱”变“强”的原因,但是如果训练样本中存在大量的噪声或者样本数据错误,就会出现过适应现象。因为这些噪声或错误点是难分类点,随着迭代的进行,它们的权值会呈指数增长,在这样的样本权重分布下,训练产生的弱分类器的错误率相对增大,从而它们在最后的加权组合中作用变得非常小。而且由于归一化,已经被正确分类的样本在过适应的情况下,权重变得非常小,可能会出现被忽视的情况,那些被迭代前期产生的弱分类器正确分类的样本,很有可能在最后组合分类器判断下的结果是错误的,最终导致退化,影响集成性能。所以,在迭代后期,要控制弱分类器对困难样本的关注,避免样本分布扭曲。
3 改进算法
针对上述问题,本文提出基于DF改进的AdaBoost算法,通过改进弱分类器选择策略,控制弱分类器之间的DF值,来避免对困难样本的过分关注。
3.1 改进弱分类器的选择策略
AdaBoost算法使用单层决策树训练弱分类器,它的一个最基本理论上的性质是可以降低训练误差,Schapire等[3]给出了AdaBoost训练误差的上界,见式(11):
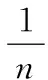
(11)
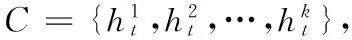
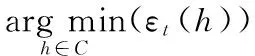
(12)
但是AdaBoost算法并没有考虑这种情况:候选的弱分类器集合中有两个或者多个弱分类器的加权误差相同(或者是相差很小),但是这些弱分类器与已经加入集成的弱分类器间的差异性有所不同,而最终选择的弱分类器的多样性不是最好的,这样就会影响集成泛化能力;而且AdaBoost会出现过适应就是因为对于某些样本过于集中关注,当增加了分类器间的多样性,就可以适度分散这种集中关注度。因此,需要在选择弱分类器的时候,加入多样性的判断。首先分析相关系数ρ,由式(3)可知,当两个基分类器的分类结果趋向不同时,ρ值为负,即n10n01>n11n00,当增大n10n01时,n11n00相应地降低,但无法保证降低的是n00,从而无法保证平均分类精度,这意味着ρ与集成的分类性能关联并不紧密,同时它的计算公式相对于其他三个多样性度量公式最为复杂。Q统计与ρ计算公式的分子相同,可以把Q统计看作是ρ的一种简化运算,因此Q存在着与ρ相同的问题。接下来分析不一致度量DM,由式(4)可知,DM越大,基分类器间的多样性越大,但同时平均精度也越低。增加多样性的目的是为了进一步提高集成算法的分类精度,所以这三种多样性度量从理论上分析都是不适合AdaBoost的。本文提出一种基于DF改进的弱分类器选择策略,如下所示:
(13)
其中:w1+w2=1,分别代表加权误差与DF值在选择策略中的比重;DFt-1,t表示候选弱分类器与上一轮迭代中已被选中弱分类器之间的DF度量值。由式(5)可知,DF变小,表示n00减少了,相对的n11+n01+n10就会增加。若增加的是n11,那么表明集成分类器的正确率提高了,若增加的是n10+n01,则表明基分类器间的差异性增大,集成多样性提高了。对AdaBoost来说,DF变小意味着两个弱分类器共同错分的样本数少了,它们各自有自己关注的困难样本,就不会对某些样本过于集中关注,避免某些样本的权值过大,进而抑制过适应。
关于w1、w2的取值,在AdaBoost过程中不是固定不变的,而是根据AdaBoost的训练情况动态调整。w2为已经加入集成的前t-1个弱分类器间的平均DF值,根据式(6)可得:
(14)
w1=1-w2
(15)
根据式(13)和(14)可知,若是迭代中的整体平均DF值有增大的趋势,就会相应地增加DFt-1,t在选择标准中比重,控制对共同错分样本过分关注,从而达到抑制过适应的目的,否则,加权误差依然是选择标准中的重要因素。这样就能在弱分类器增加多样性的同时保证其准确性。式(11)已经说明了AdaBoost最终模型的训练集误差是有上界的,这表明该算法理论上可以收敛到误差边界;而修改后算法并没有破坏AdaBoost算法框架,依然按照原来贪心策略进行迭代,这一点保证了算法的可收敛性。
3.2 基于DF的弱分类器算法
根据单层决策树算法训练出的弱分类器的函数表达式如下:
(16)
其中:b∈{-1,1}是一个指示不等号方向的参数,θ是特征阈值。假设训练样本按照第j维特征值升序排列,使得x1, j≤x2, j≤…≤xm, j,则θ的取值范围如下:
Θj={x1, j-1,xm, j+1}∪
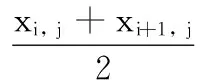
(17)
则基于DF的弱分类器算法(Weak Learning algorithm based on Double Fault, WLDF)如下:
WLDF算法。
输入:训练集S,样本分布Dt。
初始化:EDFmin=+∞,h*=null
1)
根据式(14)和(15)计算出w1和w2
2)
for 样本的每一特征j:
3)
由式(17)计算θ取值范围Θj
4)
for 每一个阈值θ∈Θj:
5)
for 不等号b∈{-1,1}:
6)
训练出一个弱分类器ht
7)
计算EDF=w1εt+w2DFt-1,t
8)
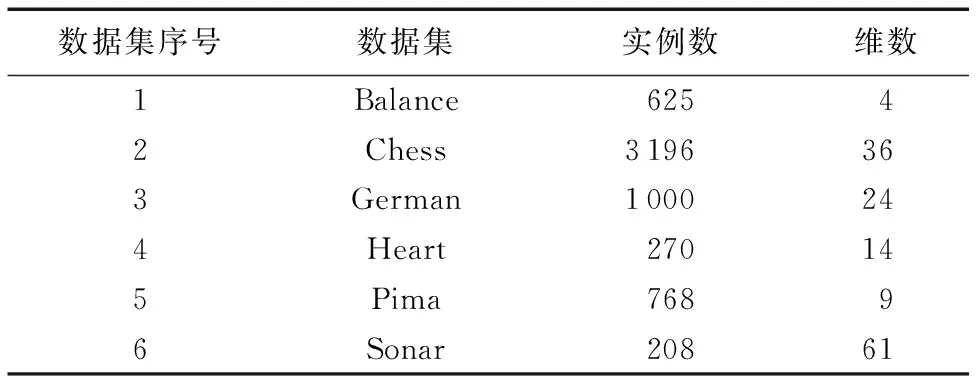
ifEDF 9) EDFmin=EDF 10) h*=ht 11) end for 12) end for 13) end for 输出:h*。 实验分为实验一和实验二。实验一研究Q、ρ、DM、DF四种多样性度量在AdaBoost算法迭代过程中的变化规律及其与集成泛化能力的相关性,实验二验证WLDF算法的有效性。实验机器配置为:Windows 10,内存4 GB,CPU 3.2 GHz,算法基于Python 2.7实现。实验数据来自UCI(University of CaliforniaIrvine Irvine)数据库(http://archive.ics.uci.edu/ml/datas-ets.html),具体信息见表2。 表2 实验数据集信息Tab. 2 Information of data sets 为充分使用数据,实验一采用10折交叉验证,实验结果如图1所示。图1分别呈现了6个数据集的多样性度量变化与测试误差变化。图1(a)~(d)4个子图分别呈现了ρ、Q、DM、DF的变化情况,其中纵坐标是多样性度量值,横坐标是迭代次数(也是基分类器数目),10次实验的每一次结果画一条实线表示,以此观察10次结果的变化规律是否相同。子图(e)中纵坐标是10次实验结果的平均测试误差。 首先,整体观察图1,可以看到四种多样性度量都在弱分类器数目增加到一定程度时,趋近一个值。观察图1中German、Heart、Pima以及Sonar数据集的实验结果,子图(a)~(d)中前阶段的线条很乱,这表明10次实验结果差别大,这时观察相应的子图(e),测试误差的变化很激烈,虽然总体方向是下降,但是曲线波动很大。而当多样性度量平稳变化时,见图1中Balance和Chess数据集的实验结果,四种多样性度量的10次结果几乎在一条线上,而再看测试误差变化,几乎没有波动,持续下降。这样定性看来,多样性与组合分类器精度之间有一定的关联。 图1 6个数据集上的实验结果 Fig. 1 Experimental results on six data sets 然后,单独看图1的子图(d),这是DF的变化曲线,每条曲线的变化都是相同的模式,先单调递增后不变,而ρ、Q、DM在不同的数据集上变化有所区别。根据DF的计算公式,可以知道,它统计的是共同错分的样本占总数的比例,而AdaBoost算法特点是关注难分的样本,随着迭代的进行,可以看到DF的值基本保持不变,说明AdaBoost算法的关注点确实集中到了这些共同错分的样本上。DF也能对组合分类器的精确度有所反映,它最后趋近的值越大,组合分类器的精度就相对越差。 通过观察图1,已经对多样性与分类精度之间的关系有了初步的直观认识,为了进行更客观地比较,采用定量分析的方法,利用皮尔逊相关系数公式如(18)所示,计算多样性度量与测试误差的相关性,结果见表3。式(18)中,x、y表示两个变量,E(x)表示x的数学期望。 (18) 表3 多样性度量与测试误差之间的皮尔逊相关系数值Tab. 3 Pearson correlation coefficient between diversity measurement and test error 分析表3可知,在Balance、Chess、German、Sonar、Pima数据集上,DF与测试误差之间的相关性均高于其他三种多样性度量;在Heart 上四种多样性度量与测试误差之间都是极弱相关。总的来说,DF与测试误差之间的相关性最高。 实验二中,使用WLDF作为AdaBoost的弱学习算法记为WLDF_Ada。为验证WLDF_Ada的有效性,实验采用10折交叉验证法,比较WLDF_Ada与AdaBoost、Bagging、随机森林(Random Forest, RF)以及文献[16]提出的R_Ada方法的10次平均测试误差,基分类器数目均为50。其中,Ada.、Bag、RF来自python机器学习工具箱sicikt-learn(http://scikit-learn.org/stable/index.html)。 表4 四种算法测试误差对比Tab. 4 Comparison of test errors of four algorithms 分析表4可知:在Balance数据集上,R_Ada取得最小测试误差,WLDF_Ada与AdaBoost次之,三者表现优于Bagging、RF;在Chess数据集上Bagging和RF优于其他三种AdaBoost算法。分析发现这是因为Chess数据属性之间存在强烈的相互影响,需要增加决策树的深度来改善分类性能,而本文实验中AdaBoost算法是以单层决策树作为弱分类器,Bagging和RF则对基分类器决策树的深度没有限制。在German数据集上,WLDF_Ada的测试误差比Bagging、RF、AdaBoost、R_Ada分别低1.05%、0.44%、2.55%,0.05%。类似地在Heart、Pima以及Sonar数据集上WLDF_Ada的测试误差比Bagging、RF、AdaBoost、R_Ada分别低了0.3%、0.74%、4.81%、3.14%;1.51%、1.14%、1.44%、1.08%以及2.57%、0.92%、2.22%、0.29%。除了在Chess和Balance数据集上,WLDF_Ada算法的表现均优于其他四种算法。单独比较WLDF_Ada与AdaBoost,除了在Balance数据集上,WLDF_Ada均比AdaBoost有不同程度上的性能提升。 多样性是影响集成学习的重要因素,合适的多样性度量可以指导基分类器的选择以及组合。本文研究了4种成对型多样性度量与AdaBoost算法表现之间的关系,实验一的结果表明随着迭代的进行,4种多样性度量值都趋于一个稳定的值,其中DF的变化模式固定。另外针对AdaBoost的过适应问题,本文改进了传统AdaBoost弱分类器的选择策略,提出了弱分类器学习算法WLDF,实验二结果表明WLDF算法可以抑制对困难样本的过分关注,增加分类器间的多样性,改善AdaBoost的分类性能。DF与AdaBoost算法的分类精度在一些数据集上关联并不紧密,下一步可以尝试根据样本权值以及弱分类器的权重,设计一个更合适AdaBoost算法的多样性度量方法。 参考文献(References) [1] SCHAPIRE R E. The strength of weak learnability [J]. Machine Learning, 1990, 5(2): 197-227. [2] BREIMAN L. Bagging predictors [J]. Machine Learning, 1996, 24(2): 123-140. [3] SCHAPIRE R E, SINGER Y. Improved boosting algorithms using confidence-rated predictions [J]. Machine Learning, 1999, 37(3): 297-336. [4] MORENO P J, LOGAN B, RAJ B. A boosting approach for confidence scoring [EB/OL]. [2017- 03- 06]. http://www.mirrorservice.org/sites/www.bitsavers.org/pdf/dec/tech_reports/CRL-2001-8.pdf. [5] 廖广军,李致富,刘屿,等.基于深度信息的弱光条件下人脸检测[J].控制与决策,2014,29(10):1866-1870.(LIAO G J, LI Z F, LIU Y, et al. Human face detection under weak light based on depth information [J]. Control and Decision, 2014, 29(10): 1866-1870.) [6] PIAO Y, PIAO M, RYU K H. Multiclass cancer classification using a feature subset-based ensemble from microRNA expression profiles [J]. Computers in Biology & Medicine, 2017, 80: 39-44. [7] KIM B, YU S C. Imaging sonar based real-time underwater object detection utilizing AdaBoost method [C]// UT 2017: Proceedings of the 2017 IEEE Underwater Technology. Piscataway, NJ: IEEE, 2017: 1-5. [8] 李文辉,倪洪印.一种改进的AdaBoost训练算法[J].吉林大学学报(理学版),2011,49(3):498-504.(LI W H, NI H Y. An improved AdaBoost training algorithm [J]. Journal of Jilin University (Science Edition), 2011, 49(3): 498-504.) [9] KROGH B A, VEDELSBY J. Neural network ensembles, cross validation, and active learning [J]. Advances in Neural Information Processing Systems, 1994, 7(10): 231-238. [10] KUNCHEVA L I. That elusive diversity in classifier ensembles [C]// Proceedings of the 1st Iberian Conference on Pattern Recognition and Image Analysis, LNCS 2652. Berlin: Springer, 2003: 1126-1138. [11] 孙博,王建东,陈海燕,等.集成学习中的多样性度量[J].控制与决策,2014,29(3):385-395.(SUN B, WANG J D, CHEN H Y, et al. Diversity measures in ensemble learning [J]. Control and Decision, 2014, 29(3): 385-395.) [12] CAVALCANTI G D C, OLIVEIRA L S, MOURA T J M, et al. Combining diversity measures for ensemble pruning [J]. Pattern Recognition Letters, 2016, 74(C):38-45. [13] 杨春,殷绪成, 郝红卫,等.基于差异性的分类器集成:有效性分析及优化集成[J].自动化学报,2014, 40(4):660-674.(YANG C, YIN X C, HAO H W, et al. Classifier ensemble with diversity: effectiveness analysis and ensemble optimization [J]. Acta Automatica Sinica, 2014, 40(4): 660-674.) [14] PARVIN H, MIRNABIBABOLI M, ALINEJAD-ROKNY H. Proposing a classifier ensemble framework based on classifier selection and decision tree [J]. Engineering Applications of Artificial Intelligence, 2015, 37: 34-42. [15] LI N, YU Y, ZHOU Z H. Diversity regularized ensemble pruning [C]// Proceedings of the 2012 Joint European Conference on Machine Learning and Knowledge Discovery in Databases, LNCS 7523. Berlin: Springer, 2012: 330-345. [16] 姚旭,王晓丹,张玉玺,等.基于随机子空间和AdaBoost的自适应集成方法[J].电子学报,2013,41(4):810-814.(YAO X, WANG X D, ZHANG Y X, et al. A self-adaption ensemble algorithm based on random subspace and AdaBoost [J]. Acta Electronica Sinica, 2013, 41(4):810-814.) [17] 曹莹,苗启广,刘家辰,等.AdaBoost算法研究进展与展望[J].自动化学报,2013,39(6): 745-758.(CAO Y, MIAO Q G, LIU J C, et al. Advance and prospects of AdaBoost algorithm [J]. Acta Automatica Sinica, 2013, 39(6): 745-758.) [18] MEDDOURI N, KHOUFI H, MADDOURI M S. Diversity analysis on boosting nominal concepts [C]// Proceedings of the 2012 Pacific-Asia Conference on Knowledge Discovery and Data Mining, LNCS 7301. Berlin: Springer, 2012: 306-317. [19] YULE G U. On the association of attributes in statistics: with illustrations from the material of the childhood society, &c [J]. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 1900, 194(252/253/254/255/256/257/258/259/260/261): 257-319. [20] KUNCHEVA L I, WHITAKER C J. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy [J]. Machine Learning, 2003, 51(2): 181-207. [21] SKALAK D B. The sources of increased accuracy for two proposed boosting algorithms [C]// AAAI ’96: Proceedings of the Workshop on Integrating Multiple Learned Models for Improving and Scaling Machine Learning Algorithms. Menlo Park, CA: AAAI Press, 1996: 120-125. [22] GIACINTO G, ROLI F. Design of effective neural network ensembles for image classification purposes [J]. Image and Vision Computing, 2001, 19(9/10): 699-707. This work is partially supported by the National Natural Science Foundation of Jiangsu Province (BK20140165). WANGLingdi, born in 1991, M.S.candidate. Her research interests include machine learning, data mining. XUHua, born in 1978, Ph.D., associate professor. Her research interests include computer intelligence, workshop scheduling, large data.4 实验
4.1 实验一的结果及分析
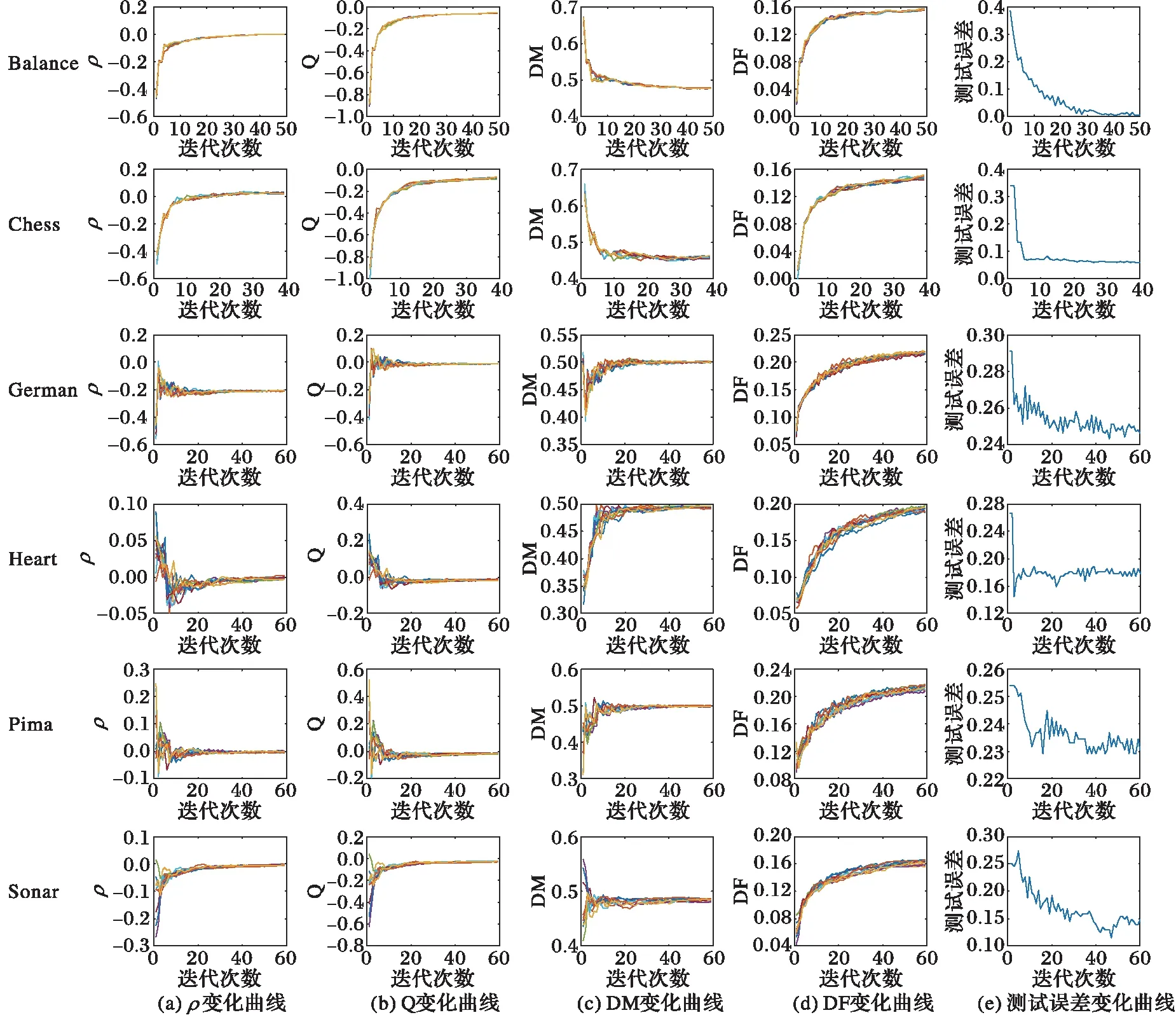

4.2 实验二的结果及分析
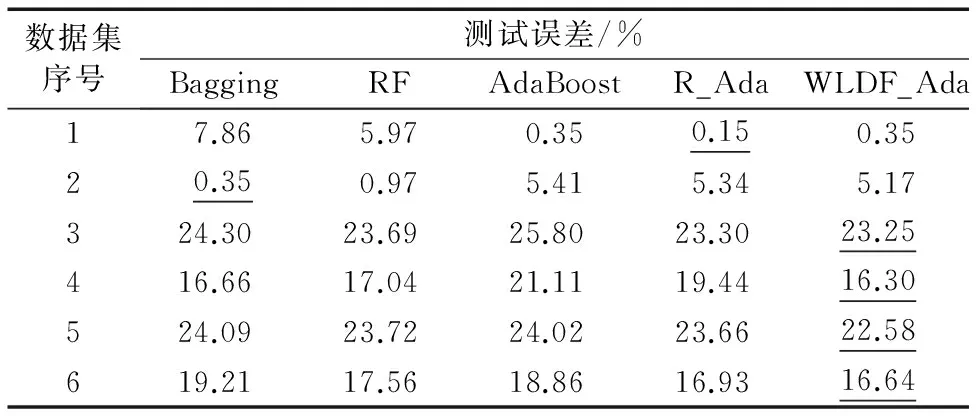
5 结语

