基于操稳特性的飞行器包线划分方法

何 敏， 余长贵

(成都飞机工业(集团)有限责任公司，成都 610091)

0 引言

飞行器在大包线内的动力学特性随高度和动压的摄动非常大，单一的控制结构体系难以满足无人机飞行对频率、阻尼等飞行品质的需求[1]。基于操稳特性的包线划分技术就是根据飞行器在包线某一个局部区域内，操纵性和稳定性具有相似的特点，将大包线划分为若干个相似动态行为的小包线区域。在每个小包线区域内，设计出无人机控制律，实现局部区域内控制性能的一致性。然后，通过控制律调度技术，达到全包线控制品质一致性的设计目标。

常用增益调度机制是通过参数“硬式”插值的方法得到控制增益[2]，“硬式插值法”没有区分飞行器不同状态点稳定性和操纵性差异，控制效果难以保障，而且后期需要大量的仿真实验来评估控制律的性能，工作量大、耗时耗力。

本文根据无人机的动力学特性连续变化的特点，应用线性系统理论的小扰动摄动法，获取到表征无人机动力学特性的参数。然后，根据飞行器局部动态特性相似特点，将全包线大区域划分为多个具有局部动态稳定性和操纵性相似的子包线区域，达到飞行器在每个子区域内具有良好的动态相似性的设计目标。

1 操纵性与稳定性分析

无人机大迎角时,操纵力矩小、飞行器反应慢、运动自然频率低；而小迎角时，操纵力矩大、响应快、频率高。因此，飞行器动态特性可以通过稳定性和操纵性来描述。

1) 稳定性。

飞行器俯仰运动模态包括短周期特性和长周期运动两个模态。短周期为角运动特性，频率高、周期短，而长周期特性为频率低、周期长。无人机飞行控制以角运动作为控制回路，因此短周期特性对无人机稳定性起主导作用。飞行器短周期动态模态可以描述为

(1)

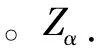
(2)

式中，s为拉普拉斯算子。短周期自然振荡频率ωsp和阻尼ξsp解析后可得

(3)

(4)

对于动稳定的飞行器，Mα值决定了短周期阻尼ξsp的大小，式(3)和式(4)可以分别简化为

(5)

(6)

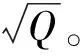
2) 操纵性。

操纵效率是指气动操纵面偏转后，改变飞行器角运动的能力，随着无人机动压的增大而增大。从短周期模态的模型可知，Mδe的大小决定了升降舵δe的操纵效能，因此该值表征了飞行器的操纵效能。

3) 动态特性。

由于σ和Mδe两种指标的意义不同，定义动态参数xk为

式中，稳定性和操纵性权重分别为a，b，满足a+b=1。

评估飞行器稳定性和操纵性的主要参数xk是连续的。根据无人机控制需求，可以将飞行包线网格化，在不同网格点，应用式(7)可以得到全包线的无人机动态参数，并通过归一化的处理，获取无人机不同包线点的相对操纵性和稳定参数分布。包线网格化后得到的动态参数的样本集合X为

X={xk|k=1,2,3,…,N}

(8)

式中,N为样本点个数。

2 划分原理

设第i个中心与第k个样本点距离为dik，定义目标性能函数为[3]

(9)

式中：μik为第k个样本点对第i个聚类中心的隶属度值;隶属度矩阵U={μik};包线中心矩阵V={vi},vi为第i个聚类中心点;N为样本容量;c为子包线数。

隶属度μik满足

0≤μik≤1

(10)

(11)

(12)

对sik求偏导数后得

(13)

sik=(-λk/mdik)1/2(m-1)

(14)

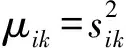
μik=(-λk/mdik)1/(m-1)

(15)

由式(11)，对式(15)求和后，得到

(16)

将式(16)代入式(15)，得到

(17)

式(12)对vi求导

(18)

令

(19)

由此可得

(20)

3 划分评价

c和m是飞行器包线划分的关键参数[4-5],为了评估结果有效性，可以从包线内的聚合度和包线间的分离度两个方面进行说明。选取划分系数PC(c)为

(21)

当上式取极值时，μik=0或1。此时对应PC(c)介于0.6到0.85之间。划分指数SC(c)为

(22)

Xie-Beni指数SXB(c)为

(23)

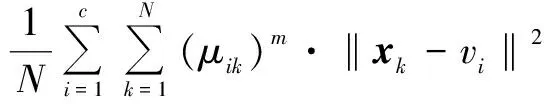
4 仿真实例

以某无人飞行器为例，该飞行器包线见图1。飞行马赫数范围为0.2～1.1，飞行高度为0～10 km。

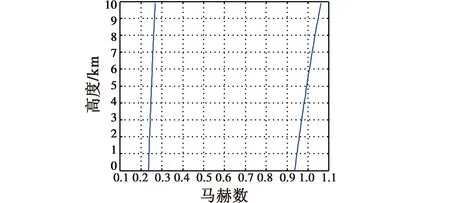
图1 某无人机飞行包线Fig.1 Flight envelope of sample UAV

在3 km高度，短周期分布见图2。

图2 高度3 km处短周期极点分布Fig.2 Short period poles distribution at a height of 3 km

分析结果表明,该飞行器的飞行速度变化对短周期运动模态具有较大影响。

根据1节方法，高度间隔0.3 km，马赫数间隔0.015，取a=b=0.5，建立动态参数样本集。划分评价系数PC(c)，SC(c)和SXB(c)指标变化情况见图3～图5。

图3 不同m和c值下PC变化情况Fig.3 PC vs m and c

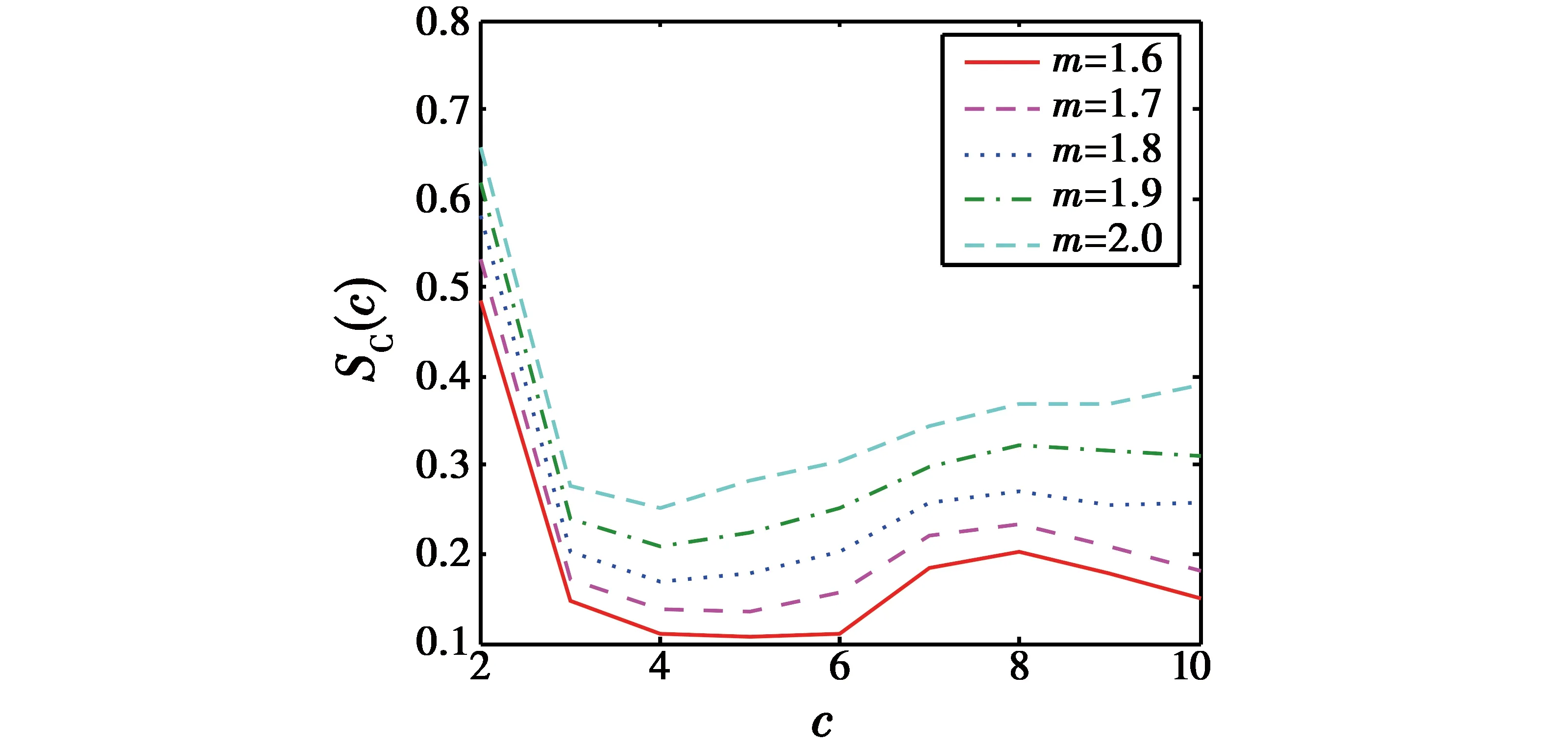
图4 不同m和c值下SC变化情况Fig.4 SC vs m and c

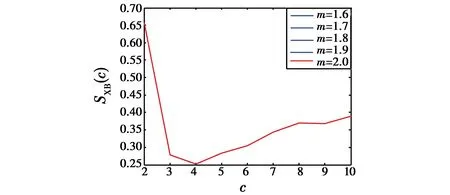
图5 SXB指标变化情况Fig.5 SXB vs m and c

从图4与图5的结果可知,SXB取极小值且SC接近极小值时，包线个数c=4。PC介于0.6～0.85之间，m介于1.6～2.2之间。当m=1.9，无人机包线划分矩阵分布及中心点见图6和图7。

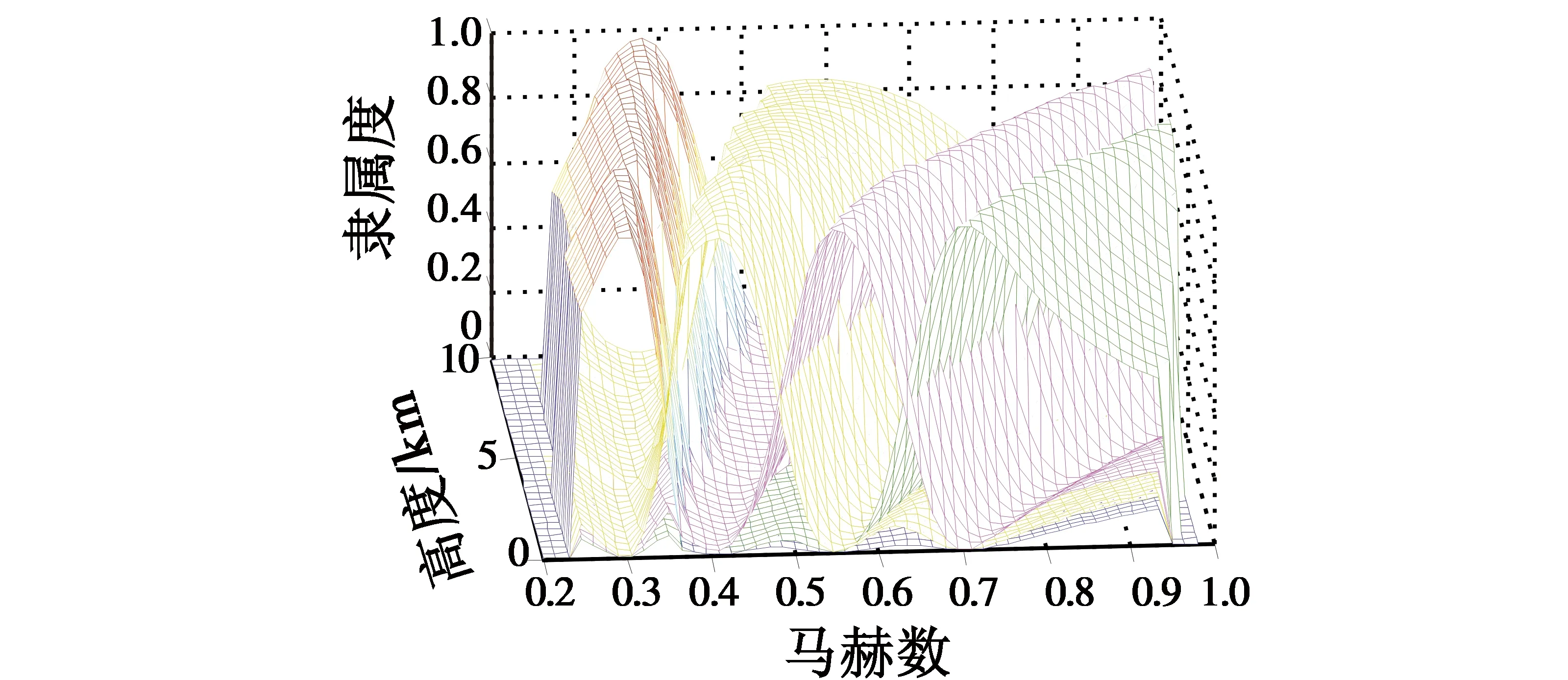
图6 划分矩阵在全包线分布情况Fig.6 The dividing matrix in the envelope

由图6可知,飞行高度对飞行器稳定性参数和阻尼值影响较小。

图7计算结果说明包线内状态点分布情况，表现出不同的动态稳定性和操纵性能，体现了各子包线的分离性和聚合性。各包线中心点的σ和Mδe如表1所示。

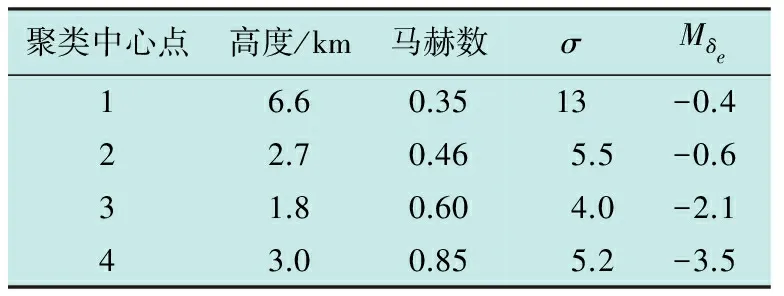
表1 包线动态参数

根据表1结果可以得到：随着马赫数增加，升降舵操纵性和稳定性变化情况，说明包线划分机制实现了对飞行器的动态特性有效划分。

图7 飞行包线划分结果Fig.7 The dividing result of flight envelope

5 结束语

本文在分析了影响飞行器动态稳定性和操纵性因素的基础上，给出了应用线性小扰动理论计算飞行器全包线稳定衰减系数和操纵性系数的方法，然后，系统地介绍了应用聚类机制划分飞行器包线过程。本文以某无人机为例，对划分方法进行了评估，结果表明，包线划分结果选取的状态点能够表征相邻区域内的动态特性一致性，子包线间的稳定性和操纵性差异明显，为控制律设计点选取提供了一种具有工程参考价值的方法。

参 考 文 献

[1] HALKIDI M,BATISTAKIS Y,VAZIRGIANNIS M.Clustering validity methods:part Ⅰ[J].ACM SIGMOD Record, 2002,31(2):40-45.

[2] GUSTAFSON D E,KESSEL W C.Fuzzy clustering with a fuzzy covariance matrix[C]//IEEE Conference on Decision and Control Including the 17th Symposium on Adaptive Processes,1978:762-768.

[3] 刘智,王勇.无人机全包线模糊鲁棒跟踪控制[J].北京航空航天大学学报，2014，40(6)：762-768.

[4] HALKIDI M,BATISTAKIS Y,VAZIRGIANNIS M.Clustering validity checking methods:part Ⅱ [J].ACM SIGMOD Record,2002,31(3):19-27.

[5 ] OOSTEROM M,BABUSKA R.Design of a gain-scheduling mechanism for flight control laws by fuzzy clustering [J].Control Engineering Practice,2006,14(7):769-781.