基于梯度下降法的四旋翼无人机姿态估计系统
刘青文, 郭剑东, 浦黄忠, 甄子洋
(南京航空航天大学,a.自动化学院; b.无人机研究院,南京 210001)
0 引言
近年来,随着无人机市场的火热,四旋翼无人机由于体积小、结构简单、操纵方便等优点吸引着越来越多科研人员的关注[1]。无人机姿态解算是实现其自主飞行的前提条件,直接决定着无人机飞行的稳定性与位置的精确性[2],因此姿态解算是无人机研究的热点领域。得益于微机电系统(MEMS)的飞速发展[3],四旋翼无人机的姿态解算系统普遍采用低成本、重量轻,便于集成、携带的航姿参考系统(AHRS),它主要由三轴陀螺仪、三轴加速度计和三轴磁罗盘组成,既可以应用于小型无人机[4],又可以应用于车辆自主驾驶[5]。然而传感器本身具有严重的时变漂移[6],陀螺仪瞬态性能良好,但会随着时间累积误差,加速度计虽没有积分误差,但处于高动态时[4],会受到附加平动或转动加速度干扰,磁罗盘易受到周围环境磁场的干扰,因此,单独采用陀螺仪或者加速度计和磁罗盘都无法独立给出精度高的姿态估计[7],所以需要采用适当的姿态解算算法对传感器数据进行误差补偿。
目前对姿态解算系统的研究常用的算法有卡尔曼滤波、互补滤波、梯度下降法等[6]。卡尔曼滤波应用比较广泛,但建立稳定可靠的姿态方程、确定合适的量测噪声以及过程噪声协方差矩阵都比较困难[3];互补滤波由于对无人机姿态估计需要重构的缺陷,且其精度低,姿态漂移严重,不适用于动态环境[8-9];本文设计了一种以STM32F427为主控制器,MPU6000和LSM303D为姿态传感器的姿态估计系统。系统采用四元数法对姿态进行描述,利用梯度下降法有效提高了四旋翼无人机姿态解算的精度。
1 硬件设计
本文姿态估计系统选择意法半导体(ST)公司的基于Cortex-M4内核的32位微控制器STM32F427VIT6为主控制器,其主频高达180 MHz,且带有单周期乘法和硬件除法,满足系统对数据运算速度的要求。航姿参考系统(AHRS)选用两款高精度的姿态传感器(内部均集成高精度的ADC),分别为MPU6000和LSM303D,构成了一个低成本、高精度的九轴姿态估计系统。姿态估计系统如图1所示。
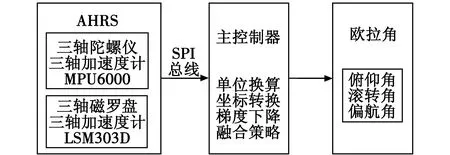
图1 姿态估计系统框图Fig.1 Block diagram of attitude estimation system
主控制器通过SPI总线(速率为22.5 MHz)读取姿态传感器数据,然后进行单位换算、坐标转换、梯度下降法解算姿态误差和融合陀螺仪角速度积分解算出欧拉角。姿态估计系统实物如图2所示。

图2 姿态估计系统实物Fig.2 The attitude estimation system
2 四旋翼无人机姿态解算
本文设计的算法步骤如下:首先,利用陀螺仪输出的角速度和四元数微分方程计算出角速度微分四元数;然后,对测得的加速度计和磁罗盘数据进行预处理,根据加速度计和磁罗盘的误差函数及其导数,得出姿态传感器的梯度公式,再利用梯度下降法消除四元数误差,得到精确的姿态四元数;最后,将陀螺仪角速度积分得到的四元数融合梯度下降法求出的姿态四元数,从而实现了姿态数据的补偿修正,提高了姿态解算精度。在姿态解算过程中只有普通的乘法和加法运算[9],这大大减轻了姿态解算的计算压力,提高了姿态解算的速度。
2.1 四元数姿态描述
在对四旋翼无人机姿态描述前,必须先建立合适的坐标系。无人机姿态描述中常用的两种坐标系分别为机体坐标系b和地理坐标系e。通常取机体的重心为机体坐标系原点,X,Y,Z轴分别与机体的纵轴、横轴和竖轴相互重合,定义无人机绕机体坐标系的Z轴转动为偏航角ψ;绕X轴转动为滚转角φ,绕Y轴转动为俯仰角θ。在忽略地球自转的情况下,可将地面坐标系看成惯性坐标系,则两个坐标系的转换可由转换矩阵表示为[4]
由于欧拉角在表示姿态时会出现“奇异点”现象,故不能实现全姿态解析。四元数在姿态描述方面成功避免了“奇异点”现象,且计算量小,实时性高,满足飞行控制的要求。四元数描述的一般形式为[10]
q=q1+q2i+q3j+q4k
(1)
忽略地球运动对四旋翼无人机的影响,四元数矩阵表达式的微分方程为[11]
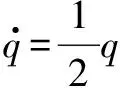
(2)
(3)
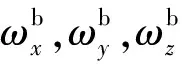
(4)
结合三角函数变换矩阵和四元数变换矩阵得出四旋翼无人机的姿态角四元数表达形式为[14]
(5)
2.2 基于梯度下降法的四元数估计
梯度下降法是沿梯度下降的方向求解表达式的最小值,其迭代表达式为
xn+1=xn-δ▽F(xn)
(6)
可知梯度下降法属于一阶收敛。式中:▽F(xn)是在xn处的梯度;负号表示梯度的负方向(即当前最快下降收敛速度);δ为梯度方向上的步长,误差函数取函数▽F(xn)的方向,即▽F(xn)/‖▽F(xn)‖。当误差函数无限接近于0时,可以认为式(6)达到了稳定解,梯度法计算完成。具体到本文中,误差函数为多元向量函数,自变量为四元数向量。算法初始化前设定经过量化后的陀螺仪、加速度计以及磁罗盘输出分别为ωb=[0ωxωyωz],ab=[0axayaz],mb=[0mxmymz],当地重力矢量和磁场矢量分别表示为ge=[0 0 0 1],ρe=[0ρx0ρz]。
2.2.1 加速度计、磁罗盘预处理
仅利用陀螺仪角速度积分获得的四元数随着时间增加,误差逐渐增大。为减少误差,可以利用四元数表征的误差函数等于0实现。由文献[15]可得加速度计表征的四元数矩阵误差函数为
(7)
上式为重力加速度在惯性坐标系中的值通过四元数法旋转到机体坐标系中的值,再减去当前加速度计的测量值。为使误差函数等于0,对式(7)进行四元数偏导,得到的导数即为雅克比矩阵[15],即
(8)
因此加速度计的梯度公式可表达为
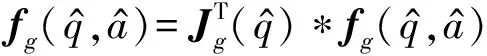
(9)
同理可得磁罗盘的误差函数及其雅克比矩阵分别为
(10)
(11)
故磁罗盘的梯度公式为

(12)
根据式(6),设经过梯度下降法预处理加速度计和磁罗盘后计算的姿态四元数为q▽,t,则
(13)
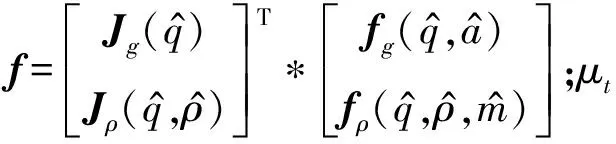
(14)
式中:Δt表示采样时间;η表示加速度计和磁罗盘的测量噪声。
2.2.2 融合策略
设式(2)求解的陀螺仪角速度姿态四元数为
(15)
加速度计以及磁罗盘预处理后的姿态四元数为q▽,t,目标姿态四元数为qest,t,则融合策略为
qest,t=αq▽,t+(1-α)qω,t0≤α≤1
(16)
式中,等式右边由两部分组成,前者适用于高速运动,后者适用于低速运动[15],因此α是一个动态值。文献[15]给出了一种α的定义,即
(17)
式中,β为四元数微分方程求解的姿态算法的发散速度,也是陀螺仪的测量误差,可通过查询传感器手册获得。
由于梯度下降法收敛速度与运动速度有关,因此用于高速运动时α必须尽可能大(过大容易导致静态性能差)。此时μt/Δt比较大,且β很小,故
(18)
将式(13)、式(15)、式(18)代入式(16)并简化得出最终的梯度下降法的姿态融合公式为
(19)
综上所述,本文的算法步骤如下:
1) 初始化,姿态传感器和陀螺仪输入参数单位规范化,确定β值;
2) 根据陀螺仪角速度利用其四元数微分方程求得角速度微分四元数;
3) 根据加速度测得值求出其误差函数及其导数;
4) 根据磁罗盘测得值求出其误差函数及其导数;
5) 利用步骤3),4)中的误差函数及其导数表征梯度公式,再利用梯度下降法求出姿态四元数q▽,t;
6) 将步骤2)中角速度微分四元数和步骤5)中姿态四元数利用融合策略推导出最终梯度下降法的姿态融合公式;
7) 将步骤6)中解算的四元数结合式(5)更新出最新姿态角;
8) 重复以上步骤,不断更新姿态角。
3 实验结果与分析
为验证本文算法,搭建四旋翼无人机飞行平台,并通过静态与动态两组实验分析姿态估计系统的有效性。实验中本文实物系统MPU6000采样频率为1000 Hz;陀螺仪角速度测量范围为±1000 (°)/s,加速度计的测量范围为±4g,磁罗盘的测量范围为±4 Gauss;数传频率为433 MHz;梯度下降法计算周期为1 ms;经过测试从传感器数据采集到完成一次梯度下降解算用时980 μs左右。
3.1 静态分析
静态分析即地面状态对姿态估计系统数据进行分析,以俯仰角为例,数据采集频率为10 Hz。图3a为系统水平放置时俯仰角的输出值,图3b为施加外力时加速度计测得的俯仰角和本文算法解算的俯仰角。
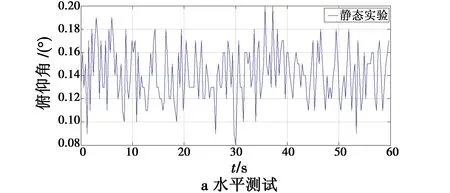
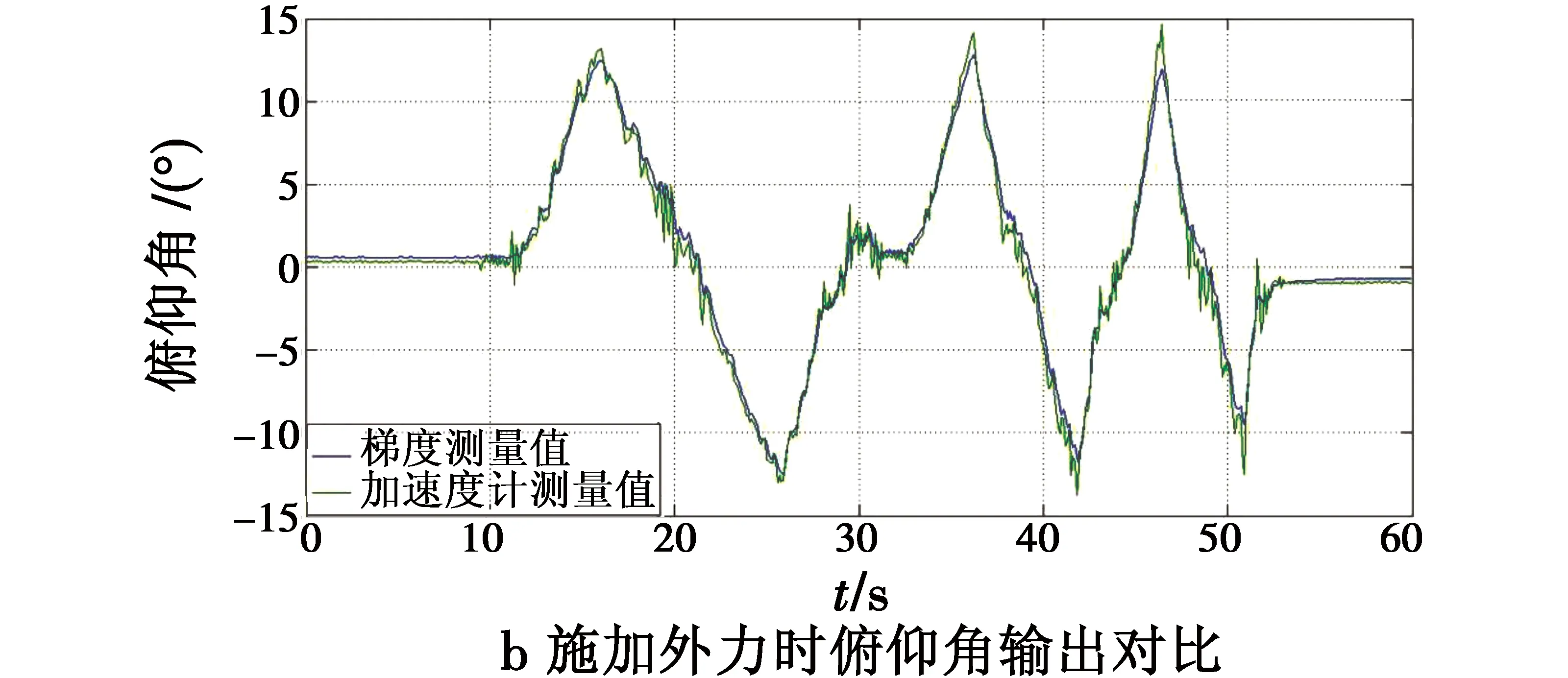
图3 静态测试Fig.3 Static test
由图3可得,水平测试时俯仰角在0.08°~0.2°之间振荡,且没有发散,有效消除了陀螺仪积分等误差;外力加载时,加速度计测得值曲线毛刺较多,本文算法解算值不仅能快速跟踪上加速度计解算值,而且曲线相对平滑,这大大削弱了加速度计带来的测量白噪声,平均跟踪偏差为0.26°。
3.2 动态分析
动态分析是将本文实物系统与Pixhawk飞控一起安装于飞行平台,通过实时飞行分析姿态估计数据,其中,Pixhawk飞控数传频率为915 MHz,姿态采样频率均为10 Hz。将Pixhawk飞控飞行日志和串口调试助手保存的数据导入Execl表中,并通过Matlab选取试飞数据进行比较分析。
当四旋翼无人机处于悬停状态时,以俯仰角为例,其输出结果如图4所示。
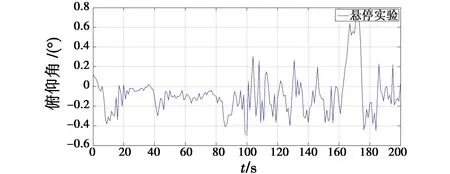
图4 悬停实验Fig.4 Hovering test
由于机体振动,俯仰角基本在(-0.5°,0.3°)之间变化,满足实际飞行时姿态解算的精度;在162 s时因风力变化导致机体振动变化,俯仰角也随之变大,12 s后机体恢复正常,俯仰角也回落到正常值。
当四旋翼无人机做俯仰、滚转、偏航运动时,如图5所示,梯度下降法测得的俯仰角、滚转角、偏航角为曲线A,Pixhawk飞控测得的俯仰角、滚转角、偏航角为曲线B。

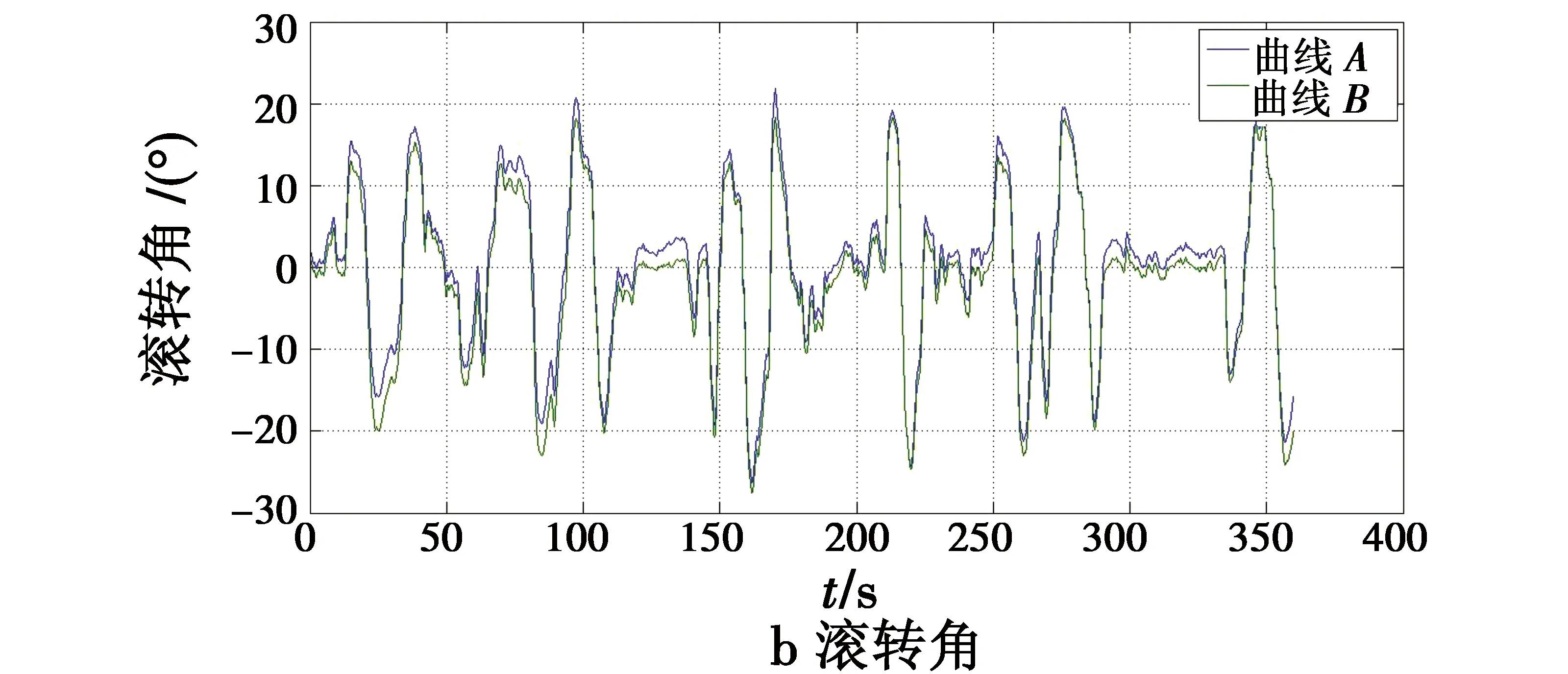
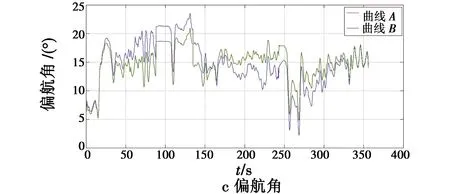
图5 俯仰、滚转、偏航运动时角度对比Fig.5 Angle contrast when pitching,rolling,or yawing
从图5可以看出,在0~360 s内,梯度下降法解算的姿态角没有发散现象,有效降低了因陀螺仪积分带来的误差;同时两种测试系统的俯仰角偏差在±2.5°以内,滚转角偏差在±3°以内,偏航角平均偏差为0.8°。因此,本文设计的姿态解算系统能够满足四旋翼无人机实际飞行的需求。
4 结论
本文在基于四元数姿态描述的基础上,设计了一种以STM32F427为主控制器,MPU6000和LSM303D为姿态传感器,利用梯度下降法预处理加速度计和磁罗盘的初始数据,并与陀螺仪角速度积分相融合的姿态估计系统。实验结果表明:梯度下降法弥补了陀螺仪角速度积分导致的累积误差,削弱了加速度计的测量白噪声;经过融合解算后的姿态角能够快速可靠地估计无人机的飞行姿态。因此,本文算法解算后的姿态角满足四旋翼无人机姿态控制的要求,为后续四旋翼无人机完成各种飞行任务奠定基础。
参 考 文 献
[1] PHAM S T,CHEW M T.Sensor signal filtering in quadrotor control[C]//IEEE Sensors Applications Symposium, 2014:293-298.
[2] 楚仕彬,袁亮.小型四旋翼无人机姿态测量仿真研究[J].计算机仿真,2015,32(2):67-73.
[3] 李文鹏,唐海洋.基于STM32的四旋翼飞行器姿态解算的研究[J].单片机与嵌入式系统应用,2016(6):13-16.
[4] 王宏昊,陈明,张坤.基于四元数与卡尔曼滤波的四旋翼飞行器姿态估计[J].微型机与应用,2016,35(14):71-73,76.
[5] 贾瑞才.基于四元数EKF的低成本MEMS姿态估计算法[J].传感技术学报,2014,27(1):90-95.
[6] 何川,李智,王勇军.基于STM32的四旋翼飞行器的姿态最优估计研究[J].电子技术应用,2015,41(12):61-64.
[7] 张浩,任芊.四旋翼飞行器航姿测量系统的数据融合方法[J].兵工自动化,2013,32(1):28-31.
[8] 梁延德,程敏,何福本,等.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统,2011,30(11):56-61.
[9] 陈亮,杨柳庆,肖前贵.基于梯度下降法和互补滤波的航向姿态参考系统[J].电子设计工程,2016,24(24):38-41.
[10] 蒋钰,谌海云,岑汝平.基于四元数的四旋翼飞行器姿态解算算法[J].制造业自动化,2015,37(12):77-80.
[11] 曹延超.基于STM32的四旋翼飞行器姿态测量系统设计[J].软件,2015,36(1):104-109.
[12] KRAJNIK T,VONASEK V,FISER D,et al.AR-drone as a platform for robotic research and education[C]//International Conference on Reseach & Education in Robotics, 2011:172-186.
[13] 刘建业,曾庆化,赵伟,等.导航系统理论与应用[M].西安:西北工业大学出版社,2010.
[14] 龙云露,陈洋,滕雄.四旋翼飞行器姿态解算与滤波[J].计算机测量与控制,2016,24(10):194-201.
[15] MADGWICK S O H,HARRISON A J L,VAIDYANATHAN R.Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//IEEE International Conference on Rehabilitation Robotics (ICORR),2011:1-7.

