基于改进遗传算法的干扰资源分配问题研究

宗思光， 刘 涛， 梁善永

(海军工程大学，武汉 430033)

0 引言

干扰方在对雷达组网进行干扰破坏的过程中，要面临的首要问题是如何将有限的干扰资源进行合理的分配，使干扰方发挥出最大的干扰效能，对整个组网进行最大程度的破坏[1]。干扰资源的分配方式在战术上大致可以分为两种：一种是集中破坏某些威胁较大的雷达；另一种是平均分配干扰火力，对整个组网的探测能力实施毁伤。在进行干扰资源分配时，首先需要在有效侦察的基础上把握雷达配置参数，然后根据敌方雷达数量以及各自的威胁程度，进行合理分配[2]。

本文针对干扰机与雷达数量对比情况的不同，建立了一对一、多对少、少对多共3种干扰资源分配模型，给出了面向组网雷达系统干扰效能的目标函数，利用改进的遗传算法，通过仿真分析，在更少的计算资源下得到更优的分配方案，从而验证了算法的有效性。

1 干扰资源建模

假设我方现有干扰资源(干扰机)的集合为J，J={J1,J2,…,Jm}，需要干扰的敌方雷达目标的集合为R，R={R1,R2,…,Rn}。我方需要合理地规划干扰机配置，以实现干扰效能的最优。因此，可将干扰资源分配问题建模成一个最优化模型。将决策变量定义为xij(xij=0或1;i=1,2,…,m;j=1,2,…,n)，当xij=1时，其代表的状态是干扰机i对雷达j实施干扰。然后，以面向组网雷达系统的干扰效能作为干扰资源分配问题的目标函数进行建模,进而可以得到0-1规划模型[3]，即

(1)

式中，m和n分别代表干扰机和雷达的数量。合理分配干扰资源的目的是力求在多干扰机对多雷达条件下，总干扰效能达到最佳效果。在实际作战问题中，各评估指标对雷达干扰效果的作用情况是不同的。于是，此处将各指标权重系数定义为wl，用来表示干扰效能指标Uij,l的重要程度值，k表示非系统性能指标个数。

在给出式(1)的约束条件之前，首先需要强调如下干扰原则：单部干扰机同一时刻只能对一部雷达实施干扰；单部雷达可同时遭受多部干扰机的进攻[4-6]。因此，干扰机与雷达数量对比情况的不同，将直接导致上述最优化问题的约束条件的差异。现分下述3种情况逐一进行讨论。

1) 一对一分配模型。

当m=n时，表示干扰机和雷达的数量相同，此时一部雷达只能受一部干扰机干扰，即得到一对一分配模型

(2)

2) 多对少分配模型。

当m>n时，表示干扰机的数量大于雷达的数量，此时一部雷达可能同时受到多部干扰机干扰，即可得到多对少分配模型：

(3)

3) 少对多分配模型。

当m

(4)

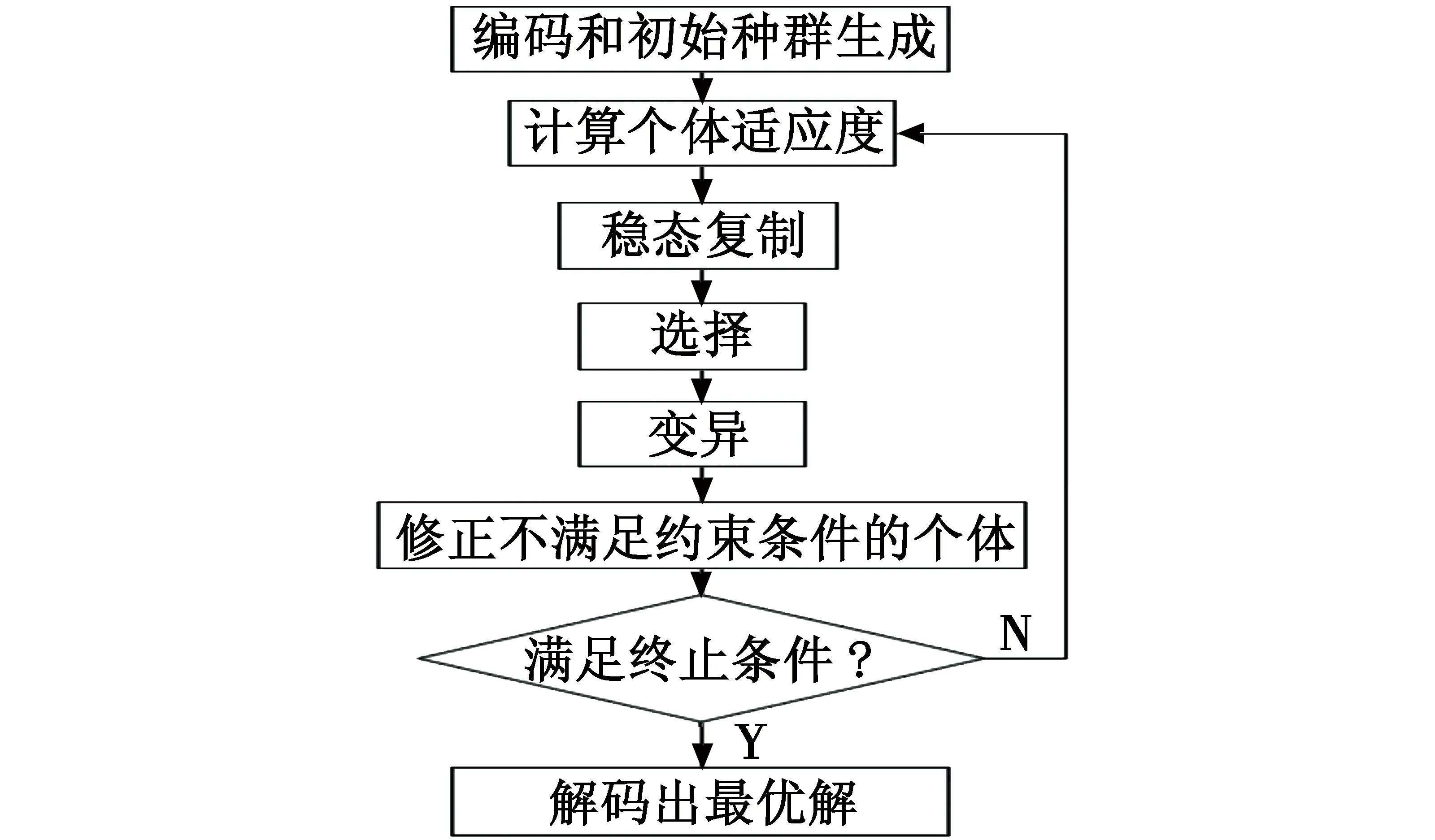
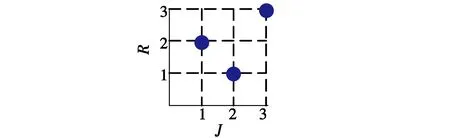
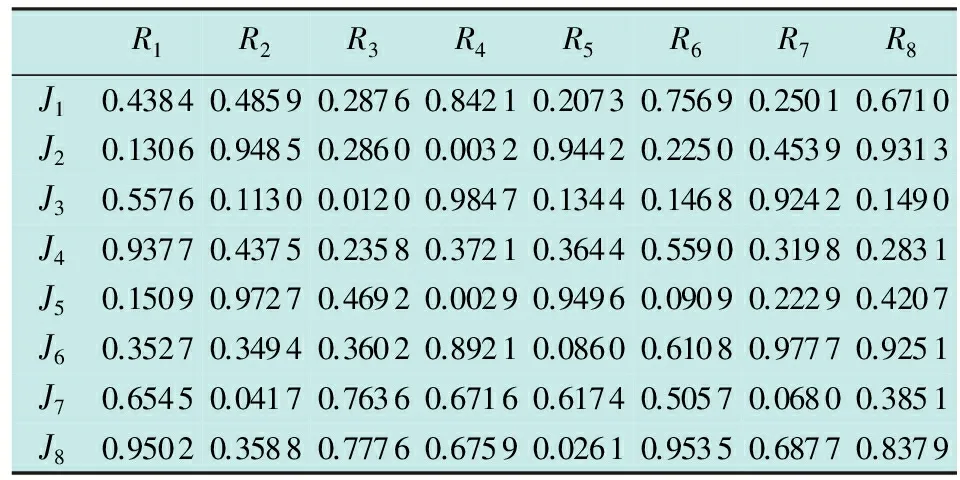
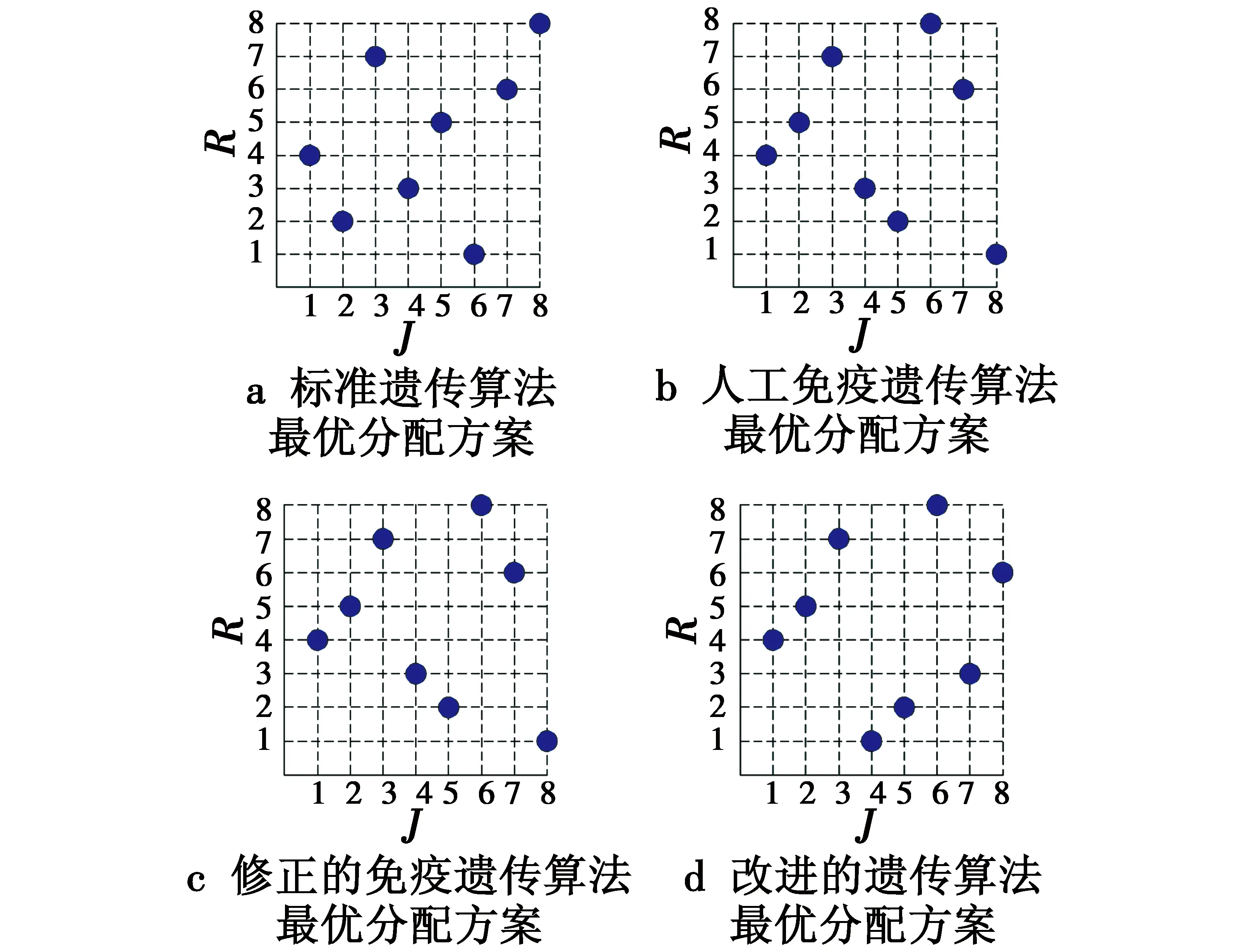
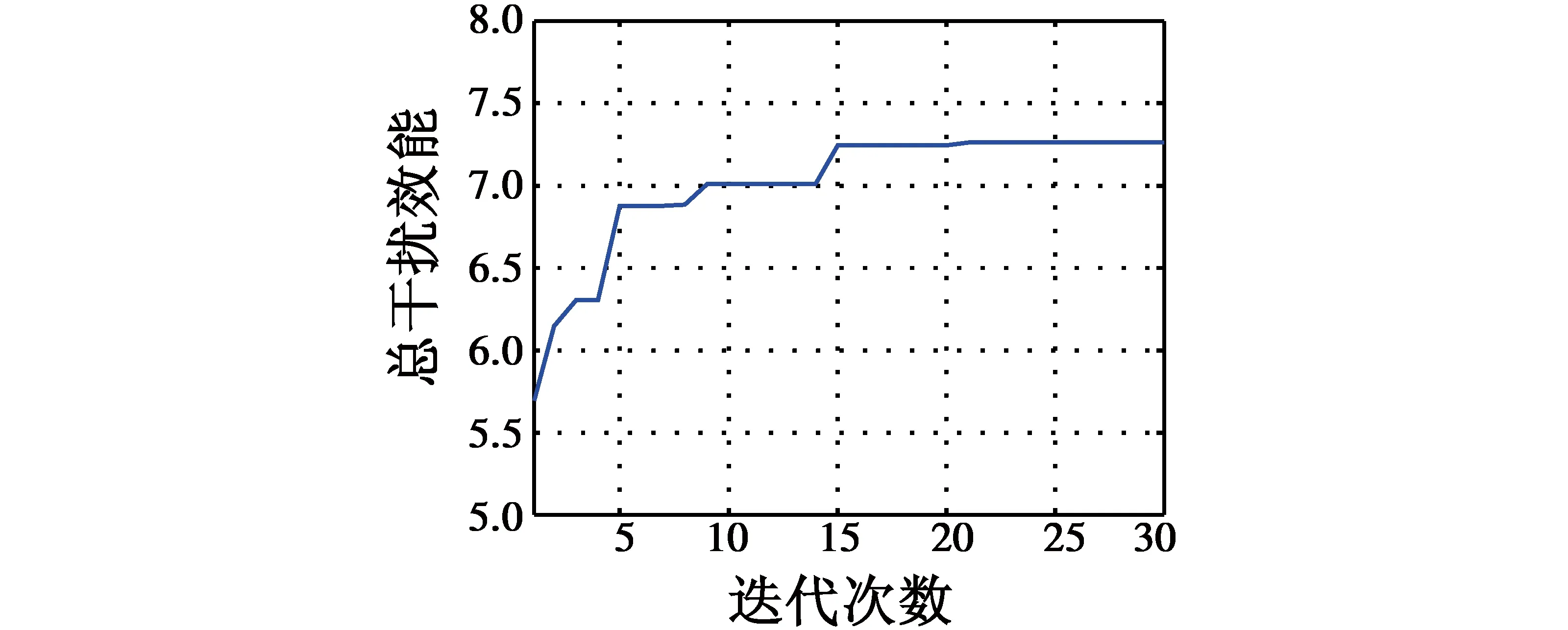
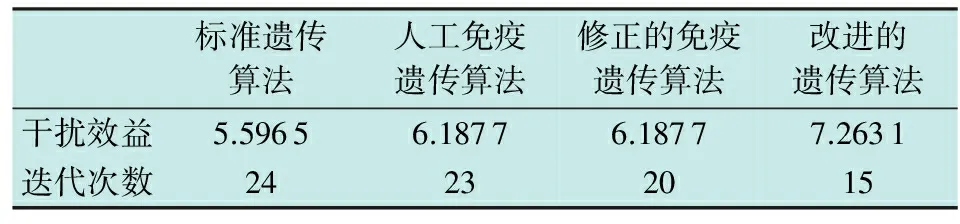
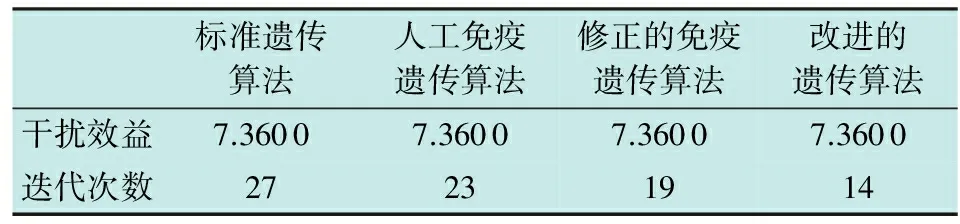
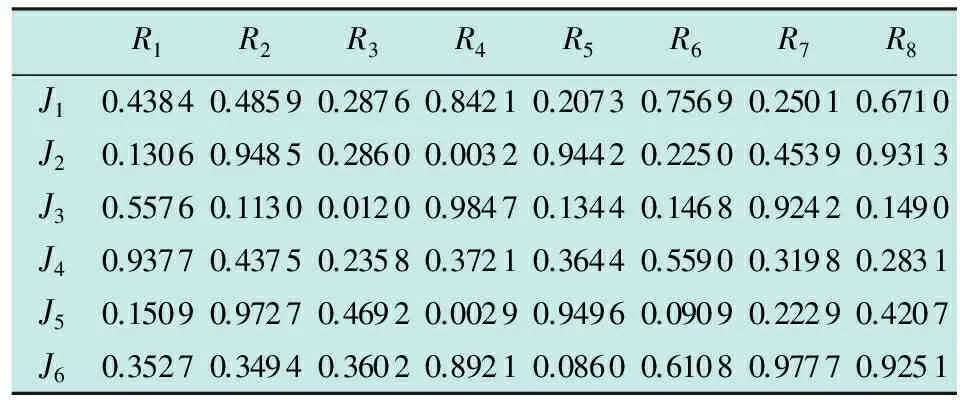
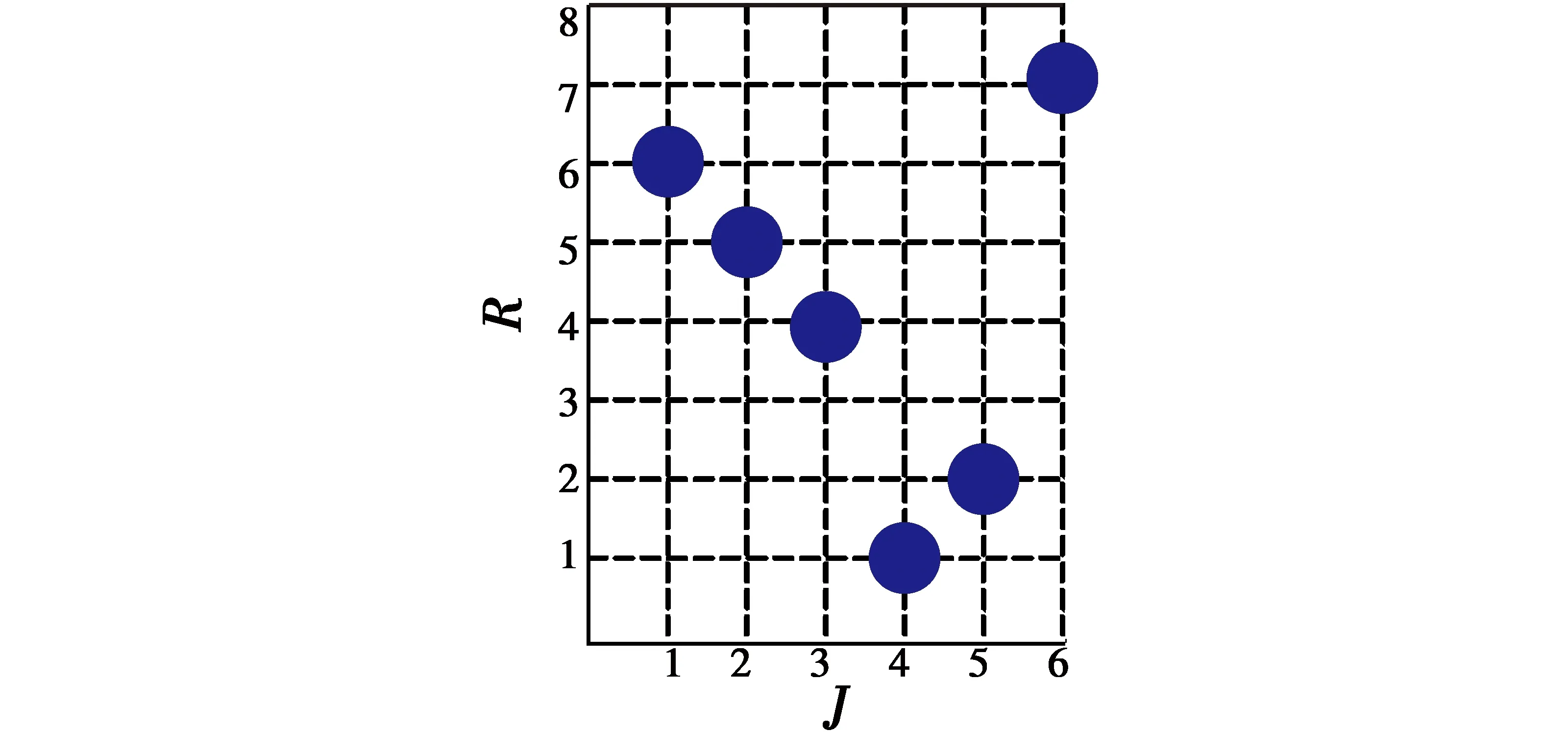
2 改进的遗传算法

遗传算法(Genetic Algorithm，GA)是一种模拟自然选择的优化算法，通过编码的方法对复杂问题进行求解。算法中，每个染色体中都被定义为一种可能的解，子代染色体通过交叉或者变异的方式产生。适应度较高的子代染色体更容易存活，数代后出现趋同效应的新染色体即为近似最优解或者是最优解[7-9]。

传统遗传算法只有选择、交叉、变异3个基本的遗传操作。根据本问题的实际情况，将遗传算法进行优化改进，增加了可以将父代精英个体的一组基因直接遗传并保留到子代的保留操作，将交叉步骤变为根据排序对群体进行筛选的选择操作。改进后的算法按以下8个步骤进行设定。

1) 编码。编码的含义是表现型映射到基因型的过程。基因型数据结构代替数据本身，通过组合构成了不同的染色体个体。每个基因位可取0或1。根据本问题的实际情况，采用近似二进制编码的形式对染色体进行编码，基因数为m×n，xij为基因项，个体染色体为

(5)

式中，k为染色体种群序号。

2) 生成初始群体。首次随机产生的N个染色体是迭代的起始点，并被定义为Q，N即为种群规模。

3) 适应度评价。适应度的评价方式是根据具体的实际问题进行定义的，用来判断解对于该问题的优劣程度，本文中其数学表达式为

(6)

通过上式计算Q中个体适应度情况。

5) 选择操作。进行适应度排序，并根据排序对群体进行筛选，适应度高的个体有更大的可能进入下一轮迭代，即

(7)

式中：p(k) 为选择概率，k=1,2,…,N；η+为最优解选择后的期望值，η-为最差解选择后的期望值;fovg为平均适应度；fmax为最优适应度。

调整η+的目的，是为了限制其取值范围在[1,2]之间，从而达到动态调整种群策略的效果。进化初期，初始种群的随机产生使个体间形状差异较大，fovg/fmax较小，η+较小，算法具有较强的空间拓展能力；进化后期，种群平均适应度逐渐趋近于最优适应度，即fovg≈fmax，η+→2，此时算法的求精能力保证了能够快速收敛，从而得到最优解。

6) 变异。按变异概率Pm选取个体进行随机位置的基因段变异。

7) 变异后个体约束条件的检查及修正。

8) 生成子代种群。将稳态复制和经自适应选择后的父代个体组成新的子代。

图1所示为遗传算法实现流程图。

图1 遗传算法实现流程Fig.1 Flow chart of the genetic algorithm

3 仿真分析

3.1 一对一分配模型

首先，假定我方3部干扰机(J1～J3)对敌方3部雷达(R1～R3)实施干扰。通过设定某时刻的装备位置信息和装备性能参数，可以得到每个干扰机对每个雷达的干扰效能指标，如表1所示。

记者从中物院核物理与化学研究所获悉，该所将与中广核研究院合作，利用中国绵阳研究堆(CMRR)开展事故容错燃料(ATF)芯块和包壳的辐照考核与评价。这标志着中广核研究院牵头的ATF国家科技重大专项已在前期材料研制的基础上迈入辐照考核的重要阶段。

表1 雷达干扰效益决策矩阵

上述为3部干扰机进攻3部雷达的资源分配问题仿真结果，可以很快观察出最优结果和分配方案，如图2所示。

图2 最优分配方案(3部干扰机，3部雷达)Fig.2 Optimal allocation scheme (three jammers and three radars)

但在实际作战中，随着干扰机和雷达数量的增加，就需要借助改进的遗传算法来对干扰资源分配问题进行求解。

下面，针对8部干扰机(J1～J8)进攻8部雷达(R1～R8)的情况，根据表2的干扰效益决策矩阵，利用遗传算法进行最优分配方案求解。

表2 一对一雷达干扰效益决策矩阵 Table 2 Radar interference benefit decision

运用改进的遗传算法进行分配决策计算，并与标准遗传算法、人工免疫遗传算法以及修正的免疫遗传算法进行对比，干扰资源分配结果如图3所示。

图3 最优分配方案(8部干扰机，8部雷达)Fig.3 Optimal allocation scheme (eight jammers and eight radars)

根据各算法最优分配结果可得到标准遗传算法、人工免疫遗传算法、修正的免疫遗传算法以及改进的遗传算法的干扰效益值分别为5.596 5，6.187 7，6.187 7，7.263 1。由此可见，本文中改进的遗传算法可以求得更优的结果，且经过更少的迭代次数便可出现最优解的收敛，如图4和表3所示。

图4 迭代次数示意图(一对一)Fig.4 Iteration times (one-by-one)

标准遗传算法人工免疫遗传算法修正的免疫遗传算法改进的遗传算法干扰效益5．59656．18776．18777．2631迭代次数24232015

3.2 多对少分配模型

针对8部干扰机进攻6部雷达的情况，根据表4的干扰效益决策矩阵，利用改进的遗传算法进行最优分配方案求解。

表4 多对少雷达干扰效益决策矩阵

运用改进遗传算法进行分配决策计算，并与标准遗传算法、人工免疫遗传算法以及修正的免疫遗传算法进行了对比，结果如图5所示。

图5 最优分配方案(8部干扰机，6部雷达)Fig.5 Optimal allocation scheme(eight jammers and six radars)

根据各算法最优分配结果可得到标准遗传算法、人工免疫遗传算法、修正的免疫遗传算法以及改进的遗传算法的干扰效益值分别为7.360 0，7.360 0，7.360 0，7.360 0。由此可见，不同算法得到了相同的最优结果。但本文的改进遗传算法需要更少的迭代次数便可出现最优解的收敛，如图6和表5所示。

图6 迭代次数示意图(多对少)Fig.6 Iteration times (more-by-less)

标准遗传算法人工免疫遗传算法修正的免疫遗传算法改进的遗传算法干扰效益7．36007．36007．36007．3600迭代次数27231914

3.3 少对多分配模型

针对6部干扰机进攻8部雷达的情况，根据表6干扰效益决策矩阵，利用遗传算法进行最优分配方案求解。

表6 少对多雷达干扰效益决策矩阵 Table 6 Radar interference benefit decision

运用改进遗传算法进行分配决策计算，分配方案如图7所示，干扰效益为5.563 9。如图8所示，迭代次数为9。单部干扰机可同时干扰多部雷达，运用合并雷达的方法，将少对多问题转化为一对一的分配问题进行分析。与本文方法相比其灵活性较差，且与本文中假定的单部干扰机一次仅能干扰单部雷达的约束条件不符，无法进行相关比较。

图7 最优分配方案(6部干扰机，8部雷达)Fig.7 Optimal allocation scheme(six jammers and eight radars)

图8 迭代次数示意图(少对多)Fig.8 Iteration times (less-by-more)

4 总结

本文建立了面向组网雷达系统干扰效能的目标函数，通过改进的遗传算法，对目标函数进行了求解,并在原有遗传算法的基础上进行了调整和改进，在算法流程中加入了适应度评价、稳态复制和选择操作，同时放弃了交叉的操作步骤,得到了更优的分配方案和更少的迭代次数，能够以更快的收敛速度得到更好的最优解。

参 考 文 献

[1] 周林，张文，娄寿春．基于遗传算法的雷达网干扰决策模型研究[J]．装备指挥技术学院学报，2002，13(3)：67-69．

[2] 张伟，平殿发，张韫．云模型在雷达干扰资源多目标优化配置中的应用[J]．指挥控制与仿真，2014，36(5)：39-44．

[3] POIROT J L,MCWILLIAMS G V.Application of linear statistical models to radar location techniques[J].IEEE Transactions on Aerospace and Electronic Systems，1974，10(6)：830-834.

[4] 沈阳，陈光永，李修和．基于0-1规划的雷达干扰资源优化分配研究[J]．兵工学报，2007，28(5)：528-532．

[5] 李昌锦，陈永光，沈阳，等．突防过程的组网雷达干扰资源优化分配[J]．火力与指挥控制，2006，31(10)：8-10,25．

[6] 李潮，周金泉．相控阵干扰机干扰防空雷达网资源分配[J]．电子信息对抗技术，2009，24(3)：48-51,61．

[7] 潘伟．基于自适应遗传算法的雷达干扰系统兵力分配[J]．电子信息对抗技术，2014，29(3)：38-41,46．

[8] ROPELEWSKI R.Detection and countermeasures to hiding attack weapons [J].Armada International,1998(5):87-89.

[9] 曹鑫，刘佳．基于免疫遗传算法的海上编队雷达网干扰规划研究[C]//国防科技管理学术会议,2009：58-62．