基于网格连通的航迹自动起始方法

张成宝, 杜 杭, 黄 磊

(南京船舶雷达研究所，南京 210003)

0 引言

航迹起始是多目标航迹处理的首要问题，只有良好的起始航迹即确认目标存在，才能解决目标的稳定跟踪问题。随着战术武器系统的迅速发展，对边扫描边跟踪(TWS)体制的现代雷达系统也提出了更高的要求，其中包括截获进入雷达威力区的新目标。目前，航迹起始的方法有很多种，主要有极大似然法[1]、序贯检测法[2]、Hough变换法[3-5]等,但是这些方法在TWS体制雷达系统中的全程全方位航迹自动起始中由于计算量大、实时性差等问题很难在工程中直接应用。

在TWS体制雷达系统中，如果每次扫描目标的检测概率很高，测量误差很低，同时虚警和杂波点迹很少，那么全程全方位的多目标航迹自动起始就比较简单，但是在实际的工程应用中，尽管运用了动目标显示(MTI)和恒虚警(CFAR)等信号处理技术，但由于热噪声、天电噪声和气象这些噪声源产生的宽带噪声，以及海浪、地物、云、雨、箔等分散单元产生的杂乱回波条件下，仍然可能有许多杂波、干扰点迹和真目标点迹一起进入数据处理系统。随着干扰和杂波的增加，系统的性能会不断下降，甚至会出现饱和过载的现象，这样传统的航迹起始方法很难实时进行航迹自动起始。对此，根据固定地物、云雨、干扰等杂波的空间分布特性，从减少参与航迹自动起始处理点迹的角度出发，提出了一种基于网格连通的航迹自动起始方法，对雷达观测空间进行网格划分并基于一定的准则形成相应的连通域，通过对连通域点迹密度的判断实现对有效起始点迹的区分和过滤，进而快速地进行航迹自动起始。

1 航迹自动起始

航迹起始是目标跟踪的第一步，是建立新的目标档案的决策方法，主要包括暂时航迹形成和轨迹确定两个方面[4]，目前主要分为手动录取起始航迹和自动录取起始航迹，一般采用逻辑法起始航迹[1]。本文主要讨论在TWS体制雷达系统中的全程全方位航迹自动起始方法。在雷达的扫描过程中，不断地对扇区数据进行处理，在全程全方位航迹自动起始时，由于不确定观测点迹的来源是目标还是杂波，所有的观测点迹都用来进行量测相关处理，形成暂时航迹，然后进行航迹稳定判断。

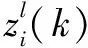
(1)

Dij(k)

(2)

式中，Dij(k)为服从自由度为p的χ2分布的随机变量。由给定的门限概率查自由度为p的χ2分布表可得门限γ，若Dij(k)≤γ，则可判定zi(k)和zj(k+1)量测关联，可以进行航迹起始。

航迹自动起始步骤如下：

1) 利用第1次扫描得到的量测作为航迹头，并根据具体的情况设定相应的关联门限，对落入初始相关波门内的第2次扫描量测建立暂时航迹；

2) 对步骤1)中建立的每条暂时航迹进行外推，以外推点为中心建立后续相关波门，波门的大小由航迹外推误差协方差确定，对第3次扫描量测进行关联判断；

3) 若后续相关波门内没有量测，则撤销此暂时航迹，或用加速度限制的扩大相关波门考察第3次扫描量测是否落在其中；

4) 继续上述步骤，直到形成稳定航迹；

5) 在历次扫描中，未落入相关波门参与数据关联判别的量测点迹(自由量测)均作为新的航迹头，转步骤1)。

2 网格划分与连通

基于网格连通的方法采用了网格的数据结构，它将空间量化为有限数目的单元，这些单元形成了网格结构[6]，通过对网格结构的分析来判断网格内的点迹能否参与自动起始。这种方法的主要优点是处理速度快，其处理时间独立于数据对象的数目，仅依赖于量化空间中每一维上的单元数目。

基于网格连通算法的基本过程是，首先将数据空间W划分为网格单元，将数据对象集O映射到网格单元中，并计算每个单元的密度，根据用户输入的密度阈值Pmin判断每个网格单元是否为高密度单元。网格方法本质上只能看作一种压缩手段，它必须与密度结合起来才能进行分析判断。另外，选取的网格大小要综合考虑关联波门、观测误差等因素[6]:如果网格选取太大，落入网格内的点迹过多，不能有效地区分出目标点迹；如果网格选取太小，会把相对密集的杂波区域分割，不能有效地区分出杂波点迹。

3 基于网格连通的全程全方位航迹自动起始

在航迹自动起始的过程中，需要对所有进入数据处理系统的点进行暂时航迹形成和轨迹确定这两个方面的处理，在杂波、干扰点迹较多的情况下，系统的计算量会大大增加，从而影响航迹自动起始的效率，严重时甚至会因为饱和过载难以起始航迹。

雷达检测到的观测点迹，无论是云雨杂波点迹、近处的地物杂波点迹还是扇形的外部干扰点迹，杂波一般都是成片出现的，而目标相对而言是孤立的。从这个角度出发，本文对雷达观测空间进行网格划分，对相邻网格单元进行连通判断，通过对连通域的分析来区分杂波域内点迹和目标点迹，从而快速地进行全程全方位航迹自动起始。

将扇区按一定的方位网格划分参数kazi和距离网格划分参数kdis进行划分，即将整个扇区划分为方位距离向上的网格集合，根据扇区内点迹的具体信息判断点迹处在哪个网格；然后对网格进行处理，将相邻的网格进行连通判断，统计连通域内的点迹密度，点迹密度超过密度阈值Pmin的连通域为杂波点迹连通域，该连通域内的点不进行自动起始。通过对点迹在自动起始前进行预判断，起始非杂波点，大大减少计算量，提高全域自动起始的实时性。基于网格连通的航迹起始流程如图1所示。

具体过程如下：

1) 进入全程全方位自动起始；

2) 根据雷达的测量误差，按一定的kazi,kdis将扇区划分成相应的网格集合，如图2中扇区网格所示；

3) 遍历所有的扇区点迹，判断点迹所在的网格，并对网格进行二值判断；

4) 遍历网格，进行距离向的网格连通判断，相邻的非空网格形成子连通域，如图2中连通域a；

5) 遍历网格子连通域，进行方位向的连通判断，将相邻的子连通域进行合并，得到新的孤立连通域，如图2中方位7和方位8上的2个子连通域形成连通域b；

6) 遍历所有的连通域进行分析，其中,点迹密度超过密度阈值的连通域判为杂波连通域，否则为目标连通域，如图2中的连通域c，d，e均为杂波连通域，其他为目标连通域；

7) 对目标连通域内的点迹进行航迹自动起始判断。

图1 基于网格连通的航迹自动起始流程Fig.1 The process of automatic track initiation based on grid connection

4 测试结果

4.1 仿真试验

4.1.1 仿真环境

假定10个目标做匀速直线运动，目标的起始位置如表1所示。雷达的扫描周期T=2 s，雷达的测向误差σx=σy=100 m，在N=20次扫描中比较不同方法的起始结果，Monte Carlo仿真试验次数M=70。

每个周期内产生的杂波个数服从泊松分布[4]，首先产生(0,1)区间上均匀分布的随机数r，然后由

(3)

确定J，即要产生的杂波个数。

表1 目标初始状态

4.1.2 仿真结果及分析

在上述仿真环境下，分别采用基于网格连通的修正Hough变换起始法(GCIH)、修正Hough变换起始法(IH)和多假设逻辑起始法(MHT)对目标进行自动起始处理，并对航迹起始结果进行比较，具体包括对算法的运行时间、跟踪成功率、虚假航迹起始概率和航迹起始周期比较。其中，目标起始概率为

C

(4)

式中：K为目标个数；M为Monte Carlo仿真试验次数；lij为第i次Monte Carlo仿真试验中，目标是否被正确起始，即

(5)

虚假航迹起始概率为

F

(6)

式中：fi为第i次Monte Carlo仿真试验中起始的虚假航迹个数；ni为第i次Monte Carlo仿真试验中起始航迹的总数。仿真结果如表2所示，图3所示为杂波数λ=200时3种起始方法的航迹起始结果比较。

表2 航迹起始结果比较

图3 模拟目标自动起始航迹Fig.3 Automatic initial tracks of simulated targets

由表1和图3可以看出： MHT法的航迹正确起始概率高，起始周期短，但是虚假航迹的起始概率高且算法的实时性较差；而IH法的起始航迹正确起始概率高，虚假航迹起始概率低，有较好的准确性，但是由于在密集杂波环境下需要处理的点迹较多，所以算法的实时性较差； GCIH法通过利用网格连通的方法过滤掉大量杂波，然后利用修正的Hough变换起始法对剩余点迹进行航迹起始，在起始速度、虚假航迹起始概率、航迹正确起始概率与修正的Hough变换起始法相当的情况下，算法的实时性得到了明显的改善，可以应用于密集杂波的实际环境。

4.2 实际应用测试

在当前视域范围(方位0°～360°，距离0～80 km)内存在9个目标，在图4中出现的点迹是30个扫描周期的累计点迹，利用采集的真实回波数据进行全程全方位航迹自动起始测试，得到MHT,IH和GCIH的不同起始方法的起始结果如图5和表3所示，图6是经过网格连通处理后的点迹结果。

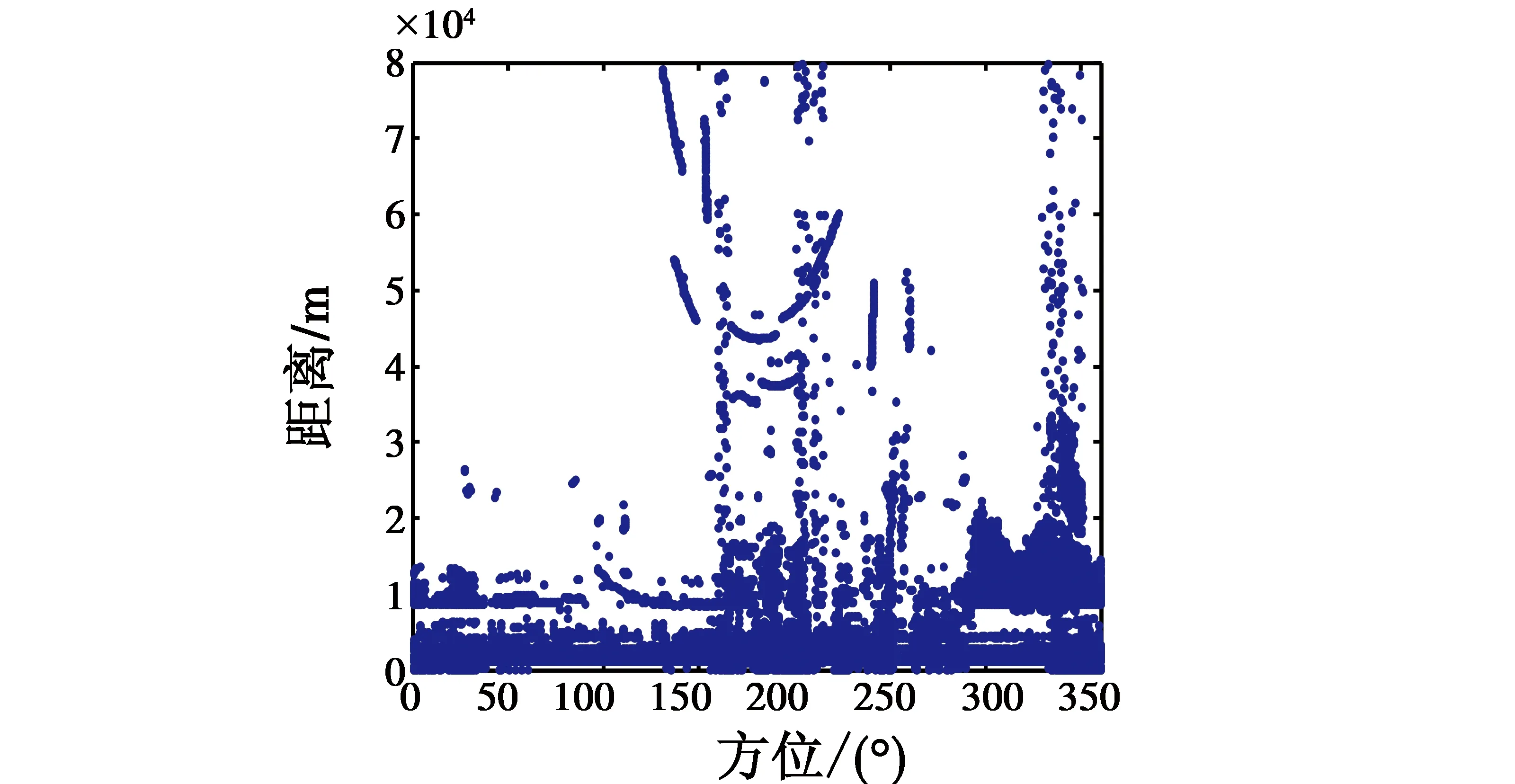
图4 原始点迹Fig.4 Original trace points

图5 真实目标自动起始航迹Fig.5 Automatic initial tracks of real targets

正确航迹虚假航迹处理时间/sMHT9116101．7IH9033．6GCIH903．7

从表3和图4的航迹起始结果比较中可以看出，由于当前雷达视域中杂波点迹较多，利用MHT法起始的虚假航迹过多，同时因为虚假航迹太多导致系统的跟踪滤波负载大，实时性差；而GCIH法和IH法均能正确地起始航迹，但是从表3中可以看出，在密集杂波环境下IH法在航迹自动起始的过程中由于参与航迹起始判断的点迹较多，存在计算量较大、实时性较差的问题，而GCIH法既能满足航迹起始准确性的要求，又具有良好的实时性。

由图6可直观地看出，因为经过网格连通处理后参与后续航迹自动起始判断的点迹数量大大减少，从而有效地降低了航迹自动起始的计算量，使得基于网

格连通的航迹自动起始方法满足了全程全方位航迹自动起始的实时性要求。

5 结束语

通过网格连通预处理的方法可以区分扇区内的目标点迹与杂波点迹，只针对目标点迹进行航迹自动起始的判断，在保证起始准确性的前提下，大大提升了航迹自动起始的实时性。本文利用实际数据对该方法进行验证，结果表明基于网格连通的全航迹自动起始方法满足工程应用的要求，具有重要的实际应用价值。

参 考 文 献

[1] TRUNK C V,WILSON J D.Track initiation in a dense detection environment[R].Washington D.C.Naval Research Lab,1987:AD-A060744.

[2] HOLMES J E.Development of algorithms for the formation and updating of tracks[C]//IEE International Radar Conference,1977:81-85.

[3] 何友,修建娟,张晶炜,等.雷达数据处理及应用 [M].2版.北京：电子工业出版社，2009.

[4] ZHANG Y H,SU X H,MA P J.Multi-Hough transform track initiation for detection target with constant acceleration[C]//International Symposium on Information Science and Engineering,2008:581-584.

[5] XIA D,CHA H,XIAO C S.A new Hough transform applied in track initiation[C]//International Conference on Consumer Electronics,Communications and Networks(CECNet),2011:30-33.

[6] 张成宝,曹伟,匡华星.基于网格连通的联合概率数据关联算法[J].电光与控制,2013,20(9):34-36.