鲁棒自适应控制的靶机蛇形机动控制律设计

李雪兵， 李春涛， 坤 娅

(南京航空航天大学自动化学院，南京 210016)

0 引言

当无人机被锁定时，如何摆脱来袭武器追击，以提高无人机执行任务时的生存率，这给机动控制技术造成巨大的困难。根据歼击机躲避来袭武器的经验可知，机动飞行能有效地降低被击落的概率，而蛇形机动是摆脱锁定追击、降低来袭武器命中率的最有效机动方式之一。蛇形机动可以增大来袭武器的跟踪误差，降低被击落的风险，对提高战场生存率大有裨益。但是蛇形机动时各通道之间耦合严重、控制指令变化剧烈、气动参数摄动大，易激发出严重的非线性，给无人机的控制造成巨大的难题，传统基于小扰动线性化的控制策略显得难以应对，然而，现代控制理论技术的发展和成熟为机动飞行控制带来契机[1]。为了克服蛇形机动中不确定性因素的影响，保证系统的鲁棒性和稳定性，采用鲁棒伺服控制(RSLQR)加自适应控制(MRAC)的策略[2]。鲁棒伺服控制保证系统的稳定性，自适应控制对模型中的不确定性进行在线补偿，共同实现对控制指令精确、快速的跟踪[3]。

1 问题表述

蛇形机动是指周期性改变无人机的滚转角，使无人机产生周期性的航向变化，以及类似蛇类爬行路线的水平航迹曲线。在蛇形机动中，航迹角和滚转角的响应能力是影响无人机蛇形机动交替变化的关键环节。航迹角和滚转角的响应速度越快，单位时间内形成的蛇形轨迹越多，则无人机的蛇形机动能力越强；反之，则越弱。因此，如何设计出具有良好控制品质的航迹角和滚转角回路是蛇形机动飞行的一项关键技术。

2 无人机动态模型简化

在惯性参考系中，描述任意时刻的运动状态需6个自由度，即3个质心运动和3个角运动。为简化建模过程，采用“平板地球假设”、“地面坐标系即惯性坐标系”、“质量不变”假设条件，运用牛顿定律建立六自由度模型[4]。

根据运动方程组可得

(1)

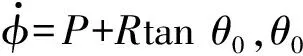
在无侧滑情况下，稳定轴角速率(Ps,Rs)与机体轴角速率(P,R)有如下关系，即

(2)

假设配平迎角为α0，从式(2)求解(P,R)得

(3)

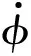
(4)

迎角、俯仰角以及爬升角满足α=θ-γ，代入式(4)得

(5)

根据小侧滑角β假设，侧滑角动态方程为

(6)

式中：δR,V,g分别表示方向舵、空速、重力加速度；Y*表示*物理量引起的侧力。

根据以上分析，无人机横侧向线性动态方程为

(7)

将式(7)改写为

(8)

式中：

(9)

显然，上述非线性的数学模型不足以完全刻画实际无人机的运动模型。因为无人机除了惯性耦合和操纵耦合之外，还存在舵面操纵效率偏差、气动数据库不准确、外界大气环境扰动、油耗导致重心变化、传感器安装位置偏差等未知扰动和不确定因素。蛇形机动时，横侧向运动剧烈、交叉耦合严重，为保证蛇形机动的控制品质，必须针对上述因素进行克服，降低它们对系统的影响。为了便于分析，本文设舵面效率偏差为Λ，模型中所有未知有界扰动为w，所有不确定因素为f(x)。根据上述分析，可得无人机的非线性数学模型为

(10)

式中:x∈Rn是系统的状态量;u∈Rm是控制输入量;Λ∈Rm×m是具有正对角元素的未知常数对角矩阵，体现控制通道中存在的舵效偏差;f(x)代表蛇形机动中所有不确定因素;wx表示和状态量相关的未知有界干扰[6]。

为了克服无人机蛇形机动过程中的有界干扰和不确定因素，本文提出了一种以鲁棒伺服控制为主，自适应控制为辅的控制器架构，控制结构如图1所示。

鲁棒伺服控制策略是通过引入积分提高系统的型别，达到抑制扰动的目的。自适应控制方法是把跟踪误差作为一个新的状态变量引入到原系统中进行系统增广，令增广系统中含有不确定因素项为零，可得到参考模型。将原系统输出和参考模型输出进行在线补偿，使系统的输出跟踪参考模型的输出，达到补偿系统中任意形式不确定性的目的。最后，将鲁棒伺服控制器和自适应控制器组成一种并联的控制结构，此结构综合了两者的特点，不仅可以提高抑制扰动的能力，提高系统的鲁棒性，而且还可以克服模型中潜在的不确定性，改善系统的响应品质[7]。

图1 鲁棒自适应控制结构Fig.1 Robust and adaptive control structure

3 控制律设计

3.1 横侧向增稳控制律设计

样例无人机采用“Λ”形尾气动布局，其滚转静不稳定(Clβ>0)，故需要增稳设计。通过引入角速率和气流角反馈达到增稳的目的，增稳的控制律为

(11)

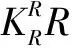
3.2 航向通道控制律设计

蛇形机动时航向通道除增稳之外，还必须具备协调转弯、快速消除侧滑角的能力[9]。在气流坐标系下，根据侧力Y的运动方程

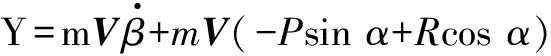
(12)

式中,(-Psinα+Rcosα)体现气流角之间的交叉耦合效应，在Y=0,α≈0°情况下，可简化为

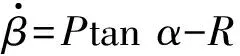
(13)

由于无人机运动存在耦合，恒定滚转角产生的附加恒定偏航角速率Rb为

(14)

该附加偏航角速率信号会使无人机在滚转过程中产生不期望的恒定偏航运动，故需要对运动耦合进行补偿。本文采用滚转角反馈加高通滤波的补偿策略，滚转角补偿策略为

(15)

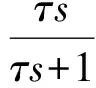
(16)

式中，τ为滤波时间常数。

3.3 滚转通道控制律设计

根据六自由度运动学方程，在惯性坐标系下的侧向速度方程为

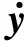
(17)

式中：u,v,w分别表示体轴系三轴速度；ψ表示偏航角。

在纵向俯仰角较小并且稳定飞行的状态下，w≈0,sinθ≈0。故可对上式进行简化得

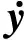
(18)

(19)

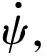
本文的控制策略将滚转通道作为机动的主控通道，航向通道控制律设计已经进行介绍，故以下主要对滚转通道进行设计。为了便于设计，本文选取迎角0°，海拔高度1 km，指示空速为141 m/s为典型工作设计点，利用小扰动线性化的原理得滚转通道的配平线性化的方程为

(20)

考虑横侧向未知有界扰动wx、不确定因素f(x)和舵面效率偏差Λ，将式(20)改写为

(21)

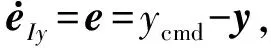
取e作为一个新的状态变量，从而构建了一个新的伺服模型，其结构为

(22)

考虑无限时间区间上的二次性能指标函数，即

(23)

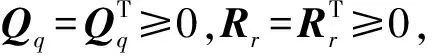
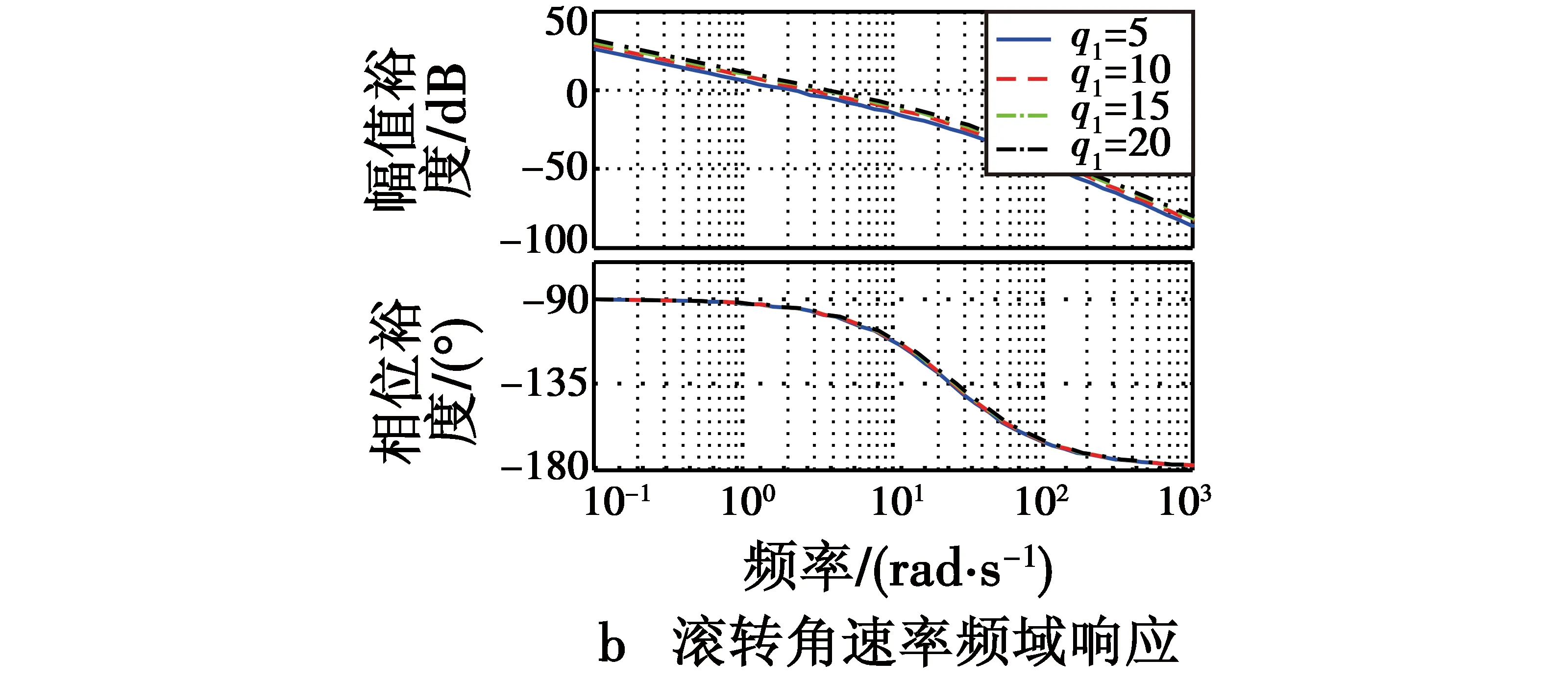
图2 滚转角速率时频域响应Fig.2 Time frequency response of roll angle rate

综合滚转角速率时频域特性的响应品质,选取q1=15,q2=1，再利用Qq阵和Rr阵求解黎卡提方程

(24)

(25)

当系统存在未知有界扰动时，运用RSLQR的方法强化对指令误差的控制作用，保证闭环系统的稳定性[11]。

根据滚转角速率阶跃响应可知，系统快、准、稳地跟踪控制指令。滚转角速率的其他响应品质见表1，其中，ts为上升时间，wb为带宽，h为幅值裕度，γ为相位裕度。

表1 滚转角速率响应品质

在完成基于RSLQR的滚转角速率内环控制律设计之后设计外环滚转角控制器，根据无人机角运动方程可得

(26)

滚转角的控制选取比例控制结构

Pcmd=KφA(φ-φcmd)

。

(27)

结合滚转角时频域特性的要求，运用根轨迹的设计方法得滚转角参数KφA=-0.8。综上所述，滚转角的控制律结构为

(28)

根据图3可以看出，滚转角满足设计要求。

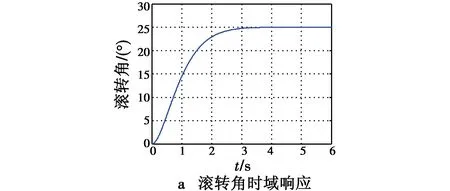
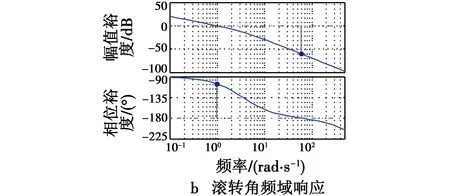
图3 滚转角阶跃响应及开环伯德图Fig.3 Step response and open-loop Bode diagram of roll angle

鲁棒伺服的控制策略虽然可以保证控制系统的鲁棒性，但对模型中存在不确定扰动却无法克服，而克服模型中的不确定因素，自适应控制有先天性优势，以下主要给出自适应的设计过程。令等式中wx=0，即只考虑系统存在不确定因素Λ和f(x)时，则等式简化为

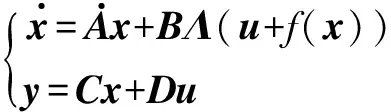
(29)

式中，f(x)是系统动态中所有不确定因素。针对蛇形机动，f(x)主要与P,β,R,δR相关。记为

f(x)=f1(P)+f2(β)+f3(R,δR)

(30)

由以上分析可知：航向通道主要作用是实现协调转弯消除侧滑角，故忽略f2(β)的影响；f3(R,δR)体现的是操纵交叉耦合不确定性，此项耦合在设计控制律之初已经考虑且与方向舵带来的滚转力矩和副翼操纵滚转力矩相比可基本忽略不计。同时假设简化后不确定函数可写成已知基本函数和未知常值系数的线性组合，故蛇形机动过程中不确定因素简化为

f(x)=f1(P)=ΘTΦ(xp) 。

(31)

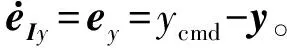
(32)

假设最终控制输入u=ubl+uad，设计目的是通过自适应补偿输入uad来抵消Λ和f(x)对系统的影响。经过鲁棒伺服设计之后，控制输入ubl为

(33)

将u=ubl+uad代入式(33)改写状态方程为

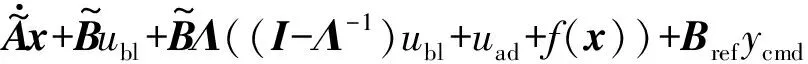
(34)

而ubl=-KLQRx，将其代入式(34)最终得

(35)

(36)

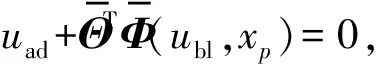
(37)

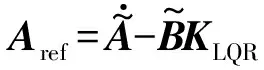
(38)

所以系统对不确定因素的补偿输入为

(39)

(40)

为了保证自适应控制系统的闭环稳定性，设计径向无界的二次Lyapunov函数

(41)

(42)

应用矢量恒等式aTb=tr(baT)得

(43)

(44)

假设自适应速率分别为Γu,ΓΘ，它们分别对应于x和Φ(xp)，故系统的自适应律为

(45)

则总的控制输入为

(46)

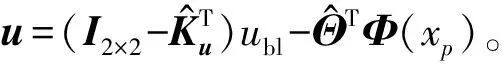
综合舵效以及滚转阻尼导数对滚转回路的影响，取f(x)=f1(P)=KPP，根据不确定性分析取Λ=0.7，KP=-1，这些特定的选择对应于控制有效性水平MδA和滚转阻尼MP，而且不确定性是有意选择的，目的是使得LQR闭环短周期开环动态不稳定。经过调试，最终选取自适应率Γbl=50,ΓP=10。线性条件响应如图4所示，RSLQR在无扰动时控制效果良好，但是在扰动存在时控制动态性能变差，而加入自适应后系统输出动态性能明显改观，证明自适应在线补偿策略起到很好的作用。

图4 系统的指令跟踪性能Fig.4 Tracking performance of system instruction

综上，蛇形机动时横侧向控制结构如图5所示。

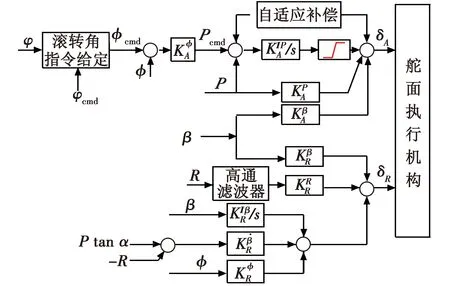
图5 横侧向蛇形机动控制律Fig.5 Lateral-directional flight control law of S maneuver

4 蛇形机动指令

图6 蛇形机动飞行过程与控制指令生成对应关系Fig.6 The relationship between flight process and control instructions generation

图中,A′,B′,C′,D′的航迹角分别为A′(φcmd),B′(φcmd),C′(-φcmd),D′(-φcmd)，其物理意义为当飞机的航迹角大于或者等于航迹角指令时，就需要通过控制改变滚转角以减小航迹角。为了得到合理的控制指令，首先对蛇形机动的运动轨迹进行分析。下面分析蛇形机动半个周期的运动状态。如图6a所示，飞机从初始状态右滚，到达A′点时，即φ=φcmd，为了减小航迹角，飞机需要进行左滚。因响应需要时间，故航迹角会由φcmd增大至φmax，记此点为E′。当航迹角再由φmax减小至φcmd，此时飞机到达B′点。

飞机到达B′点，因飞机当前处于左滚，航迹角会继续减小，当航迹角由φcmd减小到0°时，记此点为F′，此时惯性系下的侧向位移达到最大值L。此时需要减小侧向位移，所以飞机继续保持左滚。当航迹角由0°减小至-φcmd处时，飞机到达C′点。

飞机到达C′点，即φ=-φcmd，此时需要右滚以增大航迹角。同样，航迹角会先减小至-φmax再恢复到-φcmd。此时飞机到达D′点。

飞机到达D′点，飞机处于右滚，有利于航迹角减小，当航迹角由-φcmd增加到0°，此时侧偏距为0 m。蛇形机动侧向位移响应的半个周期结束。按照此过程分析，滚转角、航迹角与侧向位移之间的相位关系见图6b。根据图6b的相位关系，确定基于滚转角控制的蛇形机动指令形式为

(47)

5 蛇形机动控制律仿真

根据上述蛇形机动各物理量的动态变化过程，最终选取蛇形机动的控制指令为：滚转角指令φcmd和航迹角指令φcmd。在包线范围内，为了充分发挥样例无人机蛇形机动的能力，选取滚转角指令φcmd=25°，选取航迹角指令φcmd=20°。则根据式(47)选取蛇形机动控制指令为

(48)

选取海拔高度在1 km，指示空速141 m/s的初始飞行状态进入蛇形机动。下面选取无扰动、风扰动以及参数摄动3种情况在非线性环境下仿真。

1) 无扰动情况。

为了清晰地看出机动轨迹，图7给出水平面内两个机动轨迹周期，其余信号只给出一个周期内变化情况。在无干扰情况下，根据仿真曲线可以看出，在蛇形机动过程中侧滑角误差保持在±0.5°以内，说明方向舵协调消除误差策略起到良好的效果；根据滚转角速率响应可以看出，蛇形机动过程中滚转角速率峰值达到38 (°)/s且响应平稳无超调，说明控制策略兼顾了快速性和控制品质的要求，进一步证明了控制策略的合理性和有效性。

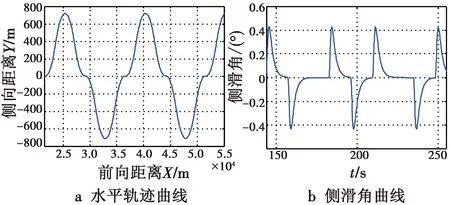
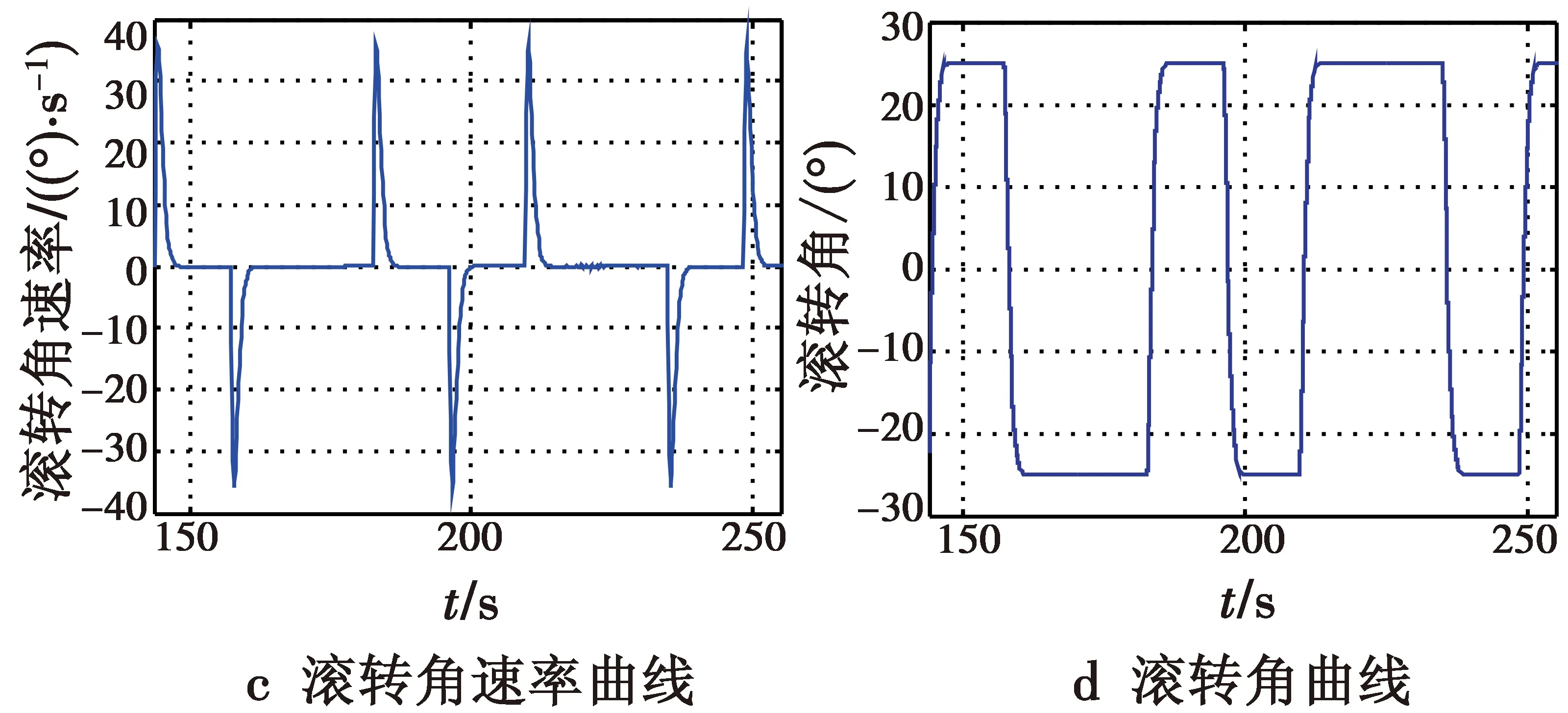
图7 正常无风扰动条件Fig.7 Normal no wind disturbance conditions

2) 风扰动情况。

为了验证控制律的鲁棒性，需要验证无人机在风扰动情况下的机动品质。在惯性坐标系下加入±15 m/s的顺逆风干扰。仿真情况如图8所示。

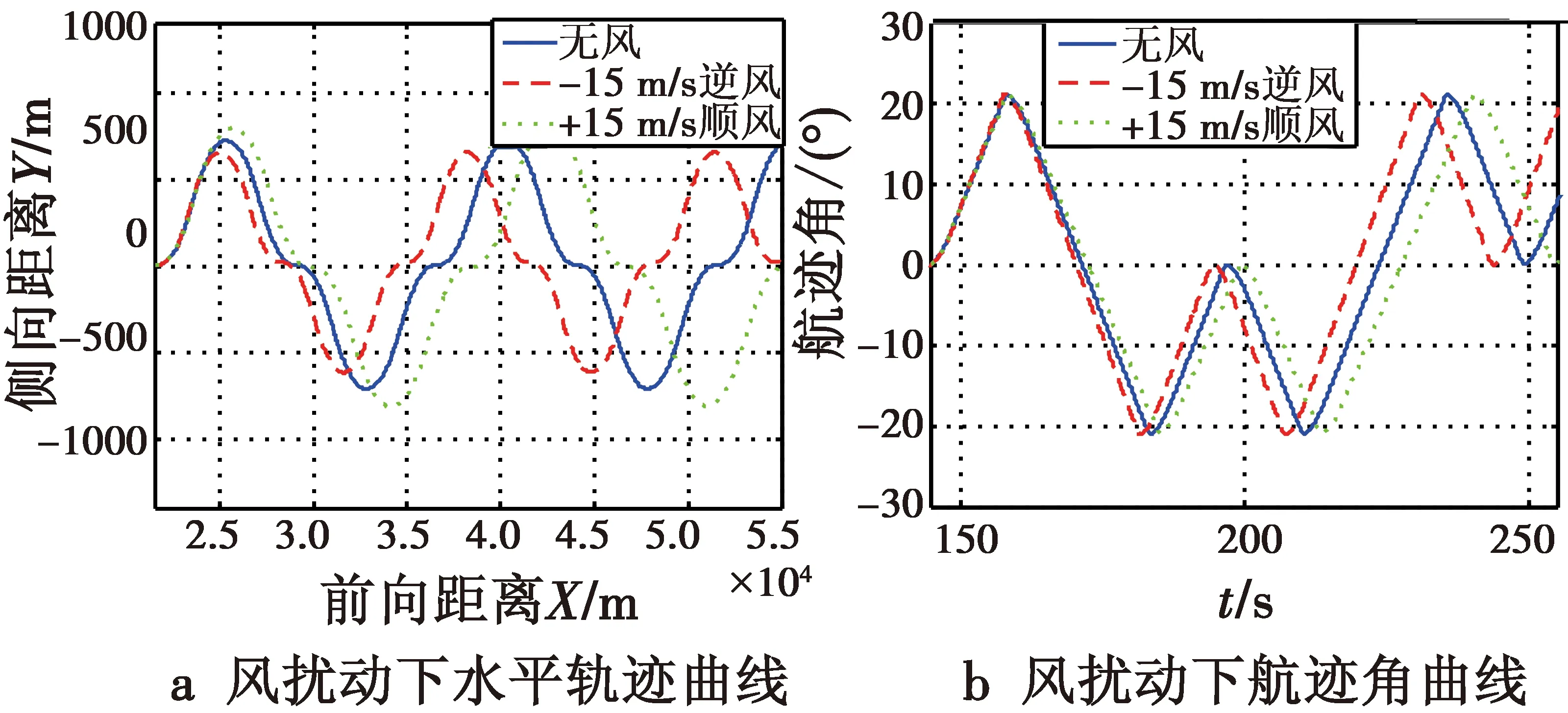
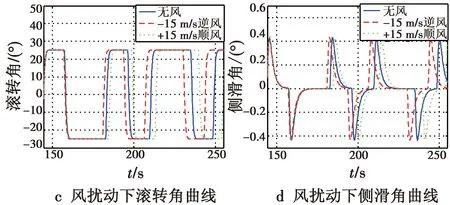
图8 顺逆风扰动条件Fig.8 Downwind and upwind disturbance conditions

根据图8可知，样例靶机在惯性坐标系下加入顺逆风后，机动飞行中各物理量较无风条件下无明显的变化，说明本文采用的鲁棒伺服控制为主、自适应为辅的主辅架构控制结构可以较好地克服大气环境变化带来的不确定性和未知扰动，进一步证明了控制策略的可行性和合理性。

3) 参数摄动情况。

选取蛇形机动的参数摄动主要包括副翼舵舵效、方向舵舵效各衰减30%和重心后拉偏0.2 m，仿真结果如图9所示。

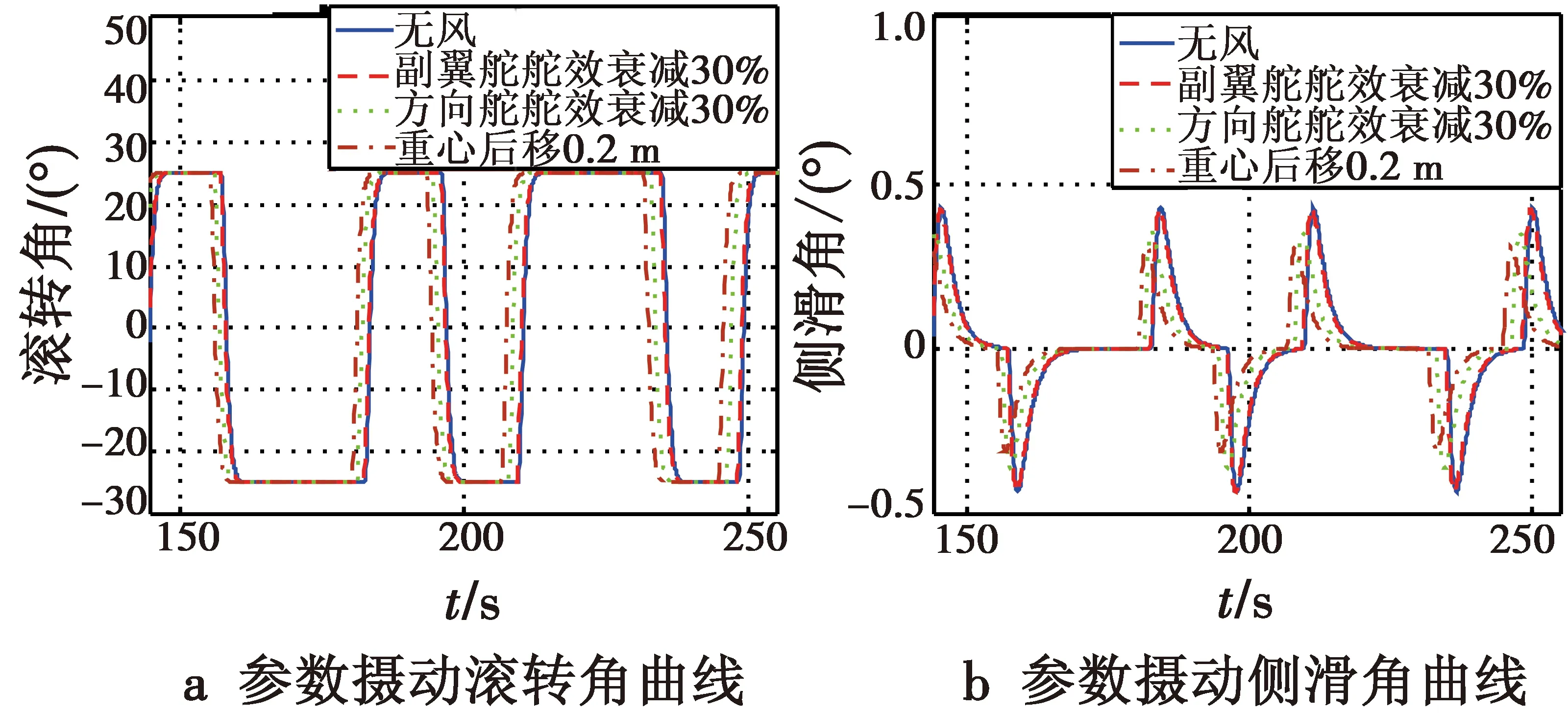
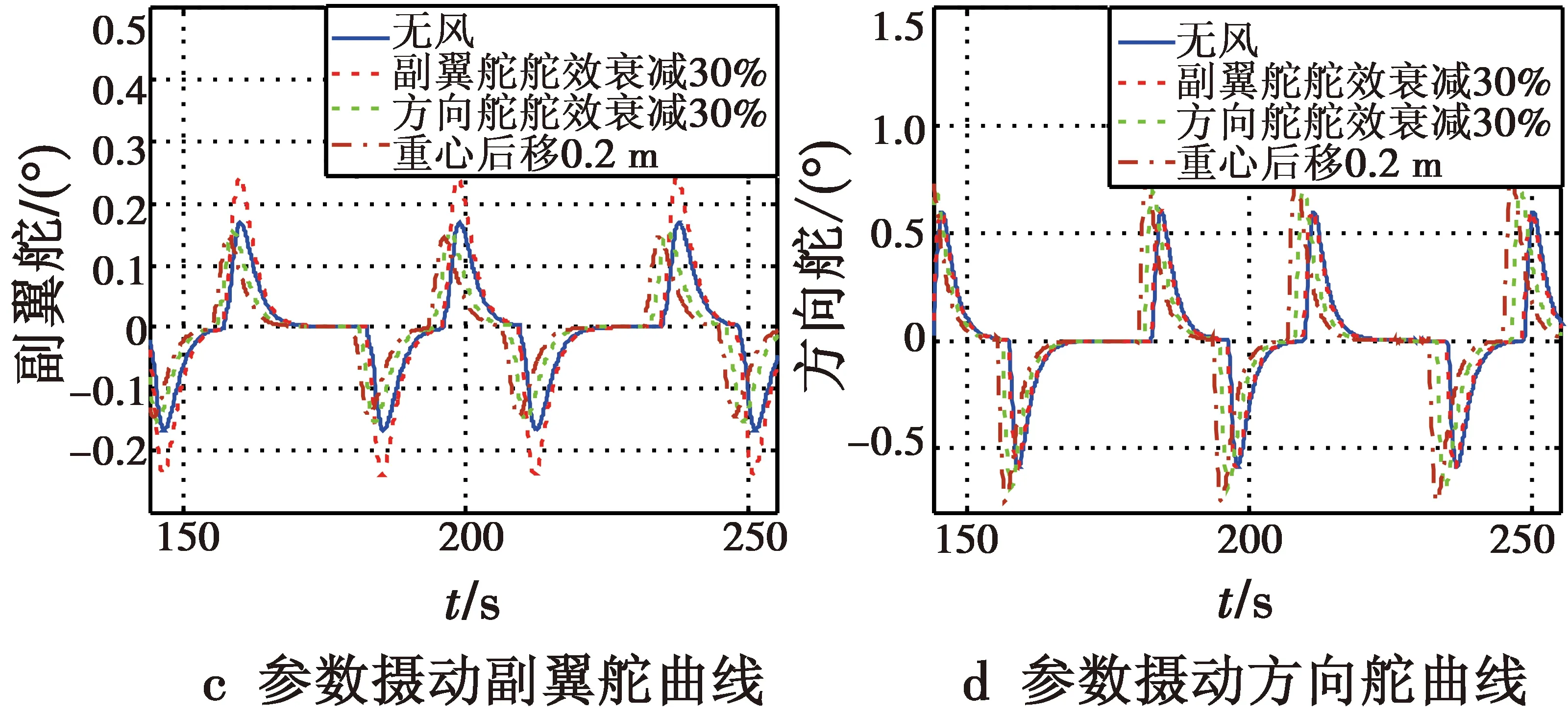
图9 参数摄动条件Fig.9 Parameter interference conditions

通过对副翼舵舵效、方向舵舵效以及重心位置分别进行拉偏仿真测试，从仿真测试结果前后对比可明显看出，样例靶机在参数摄动的干扰条件下，各物理量响应均在正常的范围内，无明显波动，说明设计的控制律可以容忍并克服此项干扰，从而证明了本文所采取的控制策略具有很强的抗扰动性能。

综合仿真结果可以看出：在无风标定情况下机动指令的选取和控制律的设计满足了蛇形机动的目标，符合控制的需求；风干扰虽然影响了航迹角的响应，造成滚转角响应的提前或滞后，导致水平面内蛇形轨迹表现出一定的不对称性，但是各信号量品质和标定情况相差无几，依然满足设计指标；参数摄动的情况下，由于设计控制律的强鲁棒性，保证了参数摄动情况下控制量零误差、高动态、无超调地跟踪控制指令，控制效果良好，满足设计需求。

6 结束语

本文以某靶机为研究对象，采用了以鲁棒伺服控制为主，以自适应控制为辅的控制策略，设计了蛇形机动的控制律。鲁棒伺服控制保证控制系统的鲁棒性能，结合自适应的补偿原理，保证了在不确定性存在的条件下依然能良好地跟踪控制指令。仿真曲线表明，在蛇形机动过程中，滚转角能够快速、稳定、零误差地跟踪控制指令且快速消除侧滑角。同时，为了验证控制律的抗扰动能力，对样例靶机在气动系数、重心位置拉偏以及风扰动环境下进行仿真测试，测试结果表明蛇形机动控制律具有良好的鲁棒性，这也更加证明本文采用的鲁棒伺服加自适应主辅架构的控制策略具有良好的理论研究和工程应用价值。

参 考 文 献

[1] WISE K A,LAVRETSKY E,HOVAKIMYAN N,et al.Ve-rifiable adaptive control:UCAV and aerial refueling[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,2008:1-6.

[2] WISE K A,LAVRETSKY E.Robust and adaptive control of X-45A J-UCAS:a design trade study[J].IFAC Proceedings Volumes,2011,44(1):6555-6560.

[3] VALAVANI L.Robust and adaptive control[J].Robust & Adaptive Control,1990(96):120-134.

[4] LAVRETSKY E,WISE K A.Robust and adaptive control[M].London:Springer,2013.

[5] CHENGDZ,SUNY,SHENTL,etal.Advancedrobust and adaptive control theory and applications[M].Beijing:Tsinghua University Press,2005:25-30.

[6] WANG J,HOVAKIMYAN N,CAO C.Verifiable adaptive flight control:unmanned combat aerial vehicle and aerial refueling[J].Journal of Guidance Control Dynamics, 2010,33(1):75-87.

[7] LIN C F,CLOUTIER J R,EVERS J H.High-perfor-man-ce,robust,bank-to-turn missile autopilot design[J].Journal of Guidance,Control & Dynamics,2012,18(1):46-53.

[8] 周丽,姜长生,文杰,超机动飞行的非线性鲁棒自适应控制系统研究[J].系统工程与电子技术,2008,30(4)：710-714.

[9] 李卫星,李秀娟,李春涛,等.飞翼无人机的一种鲁棒自适应控制律设计方法[J].电光与控制,2014,21(7):19-23.

[10] 张明廉.飞行控制系统[M].北京：国防工业出版社,1984.

[11] 杨艺,陈欣,李春涛.基于主-辅控制架构的无人机鲁棒飞行控制律设计[J].华南理工大学学报：自然科学版,2014(9):90-95.