基于改进型小波神经网络的电子战无人机作战效能评估研究
陈 侠, 胡乃宽
(沈阳航空航天大学自动化学院,沈阳 110136)
0 引言
电子战无人机是一种常用的军用无人机,担负着电子干扰、对敌防空压制和电子支援等作战任务。由于作战理念的不断更新和现代化武器的不断列装,作战环境越来越复杂多变,因此有必要预先对电子战无人机的作战效能进行评估。为了客观准确地对电子战无人机作战效能进行评估,本文提出了基于遗传算法(GA)优化小波神经网络(WNN)的电子战无人机作战效能评估方法。小波神经网络是一种结合小波函数和人工神经网络两者优点的新型神经网络,具有较强的函数逼近能力。除此之外,该方法还解决了贝叶斯网络[1]、灰色关联分析法[2]、层次分析法[3]、ADC法[4]、模糊推理法[5]等传统方法需要专家评估出各个作战效能影响因素的权重的缺点,降低了作战效能评估的主观性。但是小波神经网络应用于电子战无人机作战效能评估时,需要选择合适的初始小波神经网络连接权值和伸缩平移尺度才能获得精确的效能评估结果[6]。而以往小波神经网络的初始小波神经网络连接权值和伸缩平移尺度是根据经验来选取的,因此具有一定的局限性[7]。为了解决人为设定初始小波神经网络连接权值和伸缩平移尺度的盲目性,本文采用遗传算法寻找最优的初始小波神经网络连接权值和伸缩平移尺度。遗传算法是一种通过模拟自然进化过程搜索最优解的算法,该算法可通过随机选择、交叉和变异操作,搜索到最优的初始小波神经网络连接权值和伸缩平移尺度,使得小波神经网络表现出更加优异的性能[8]。因此,本文采用基于遗传算法优化小波神经网络(WNN Optimization Based on GA,GA-WNN)的评估模型对电子战无人机作战效能进行评估,并通过仿真实验证明了该方法具有较高的评估精度。
1 评估指标体系
虽然影响电子战无人机作战效能的因素是复杂的,但没有必要分析所有的影响因素,只需要考虑影响作战效能的关键因素。为了科学合理地选择作战效能评估的指标,本文采用增L减R法对评价指标进行优化,得出了指标数量相对较少的评价指标体系[9]。其中,选择平台能力、任务能力、生存能力、人员操作水平、敌方防御能力、环境影响系数作为主要评价指标。
1) 平台能力能够反映无人机的性能,与航程、留空时间、实用升限、最大载荷等因素密切相关;
3) 生存能力指无人机在执行任务的过程中合理规避威胁能力及安全撤离战场的能力;
4) 人员操作水平反映了人机结合能力,与人员素质、人机界面和系统自动化程度有密切关系;
5) 敌方防御能力与作战效能存在一定的联系,而作战效能是武器系统在作战应用中所取得的作战效果;
6) 环境影响系数分为自然环境影响系数和人为环境影响系数,对电子战无人机作战效能评估会产生一定的影响。人为环境影响系数与电磁干扰等影响因素密切相关;自然环境影响系数与风力、降雨量等因素具有一定的联系。
2 小波神经网络
小波神经网络将BP神经网络(BP Neural Network,BPNN)隐含层节点的激活函数采用小波函数进行替代[10]。输入层和隐含层之间的层间权值以及隐含层的阈值分别是用小波函数的尺度伸缩系数和时间平移系数进行替代的,因此兼顾了BPNN的激活函数的性质和BPNN的拓扑结构,具有较强的函数逼近能力。Kolmogorov证明,具有一个隐含层的神经网络能够实现任意精度的非线性映射[11],因此本文采用的就是单隐含层的小波神经网络结构,其拓扑结构如图1所示。
图1中:q1,q2,…,qm是小波神经网络的输入参数;A1,A2,…,Ak是小波神经网络的输出参数;wij和wjk是小波神经网络的权值;m表示输入层节点数量。
履带式行走机构在清洁机器人行驶过程中,与作业面接触的部分履带紧紧地吸附在工作平面上。驱动链轮对履带节施加一个切向的作用力,履带节给驱动链轮一个反向的作用力,这个反作用力是推动清洁机器人向前行驶的驱动力[7]。当驱动力足以克服自身重力和履带节与其滑轨之间摩擦阻力时,清洁机器人就会向前滑动前行[8]。
在输入信号序列为q1,q2,…,qm时,隐含层的计算式为
(1)
式中:h(j)为隐含层第j个节点的输出;hj为小波基函数;bj为小波基函数的平移因子;aj为小波基函数的伸缩因子。
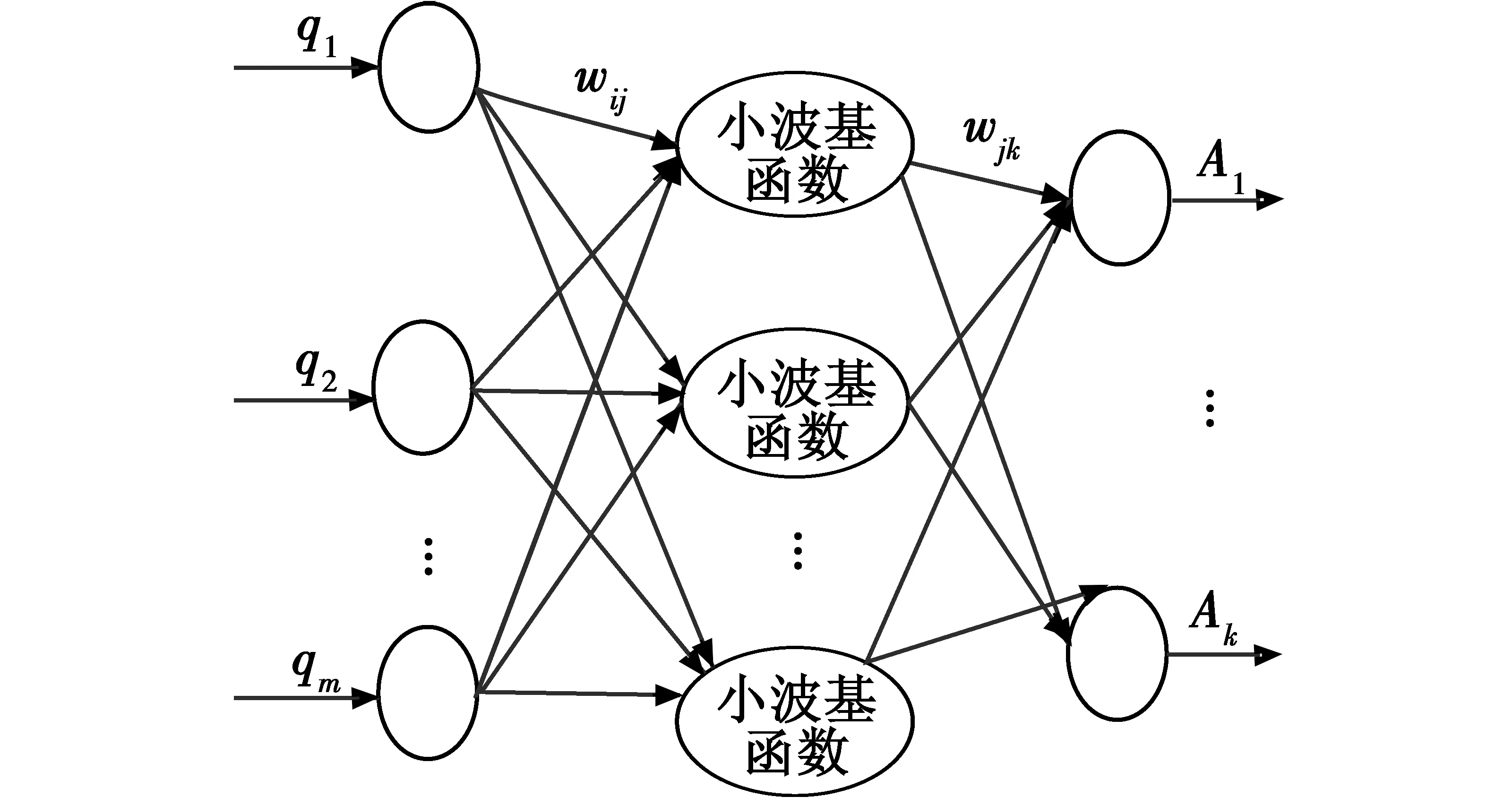
图1 小波神经网络拓扑结构Fig.1 The topology structure of WNN
尽管S型激活函数常被BPNN所采用,然而小波神经网络通常选择小波基函数作为激活函数。其中,常用的小波基函数有Haar小波、墨西哥草帽小波、高斯小波、Morlet小波。根据本文所研究的电子战无人机作战效能评估的实际问题,挑选高斯小波为相应的激活函数。图2所示为高斯小波函数的函数曲线[12],其中,t是小波神经网络基函数的支撑域。
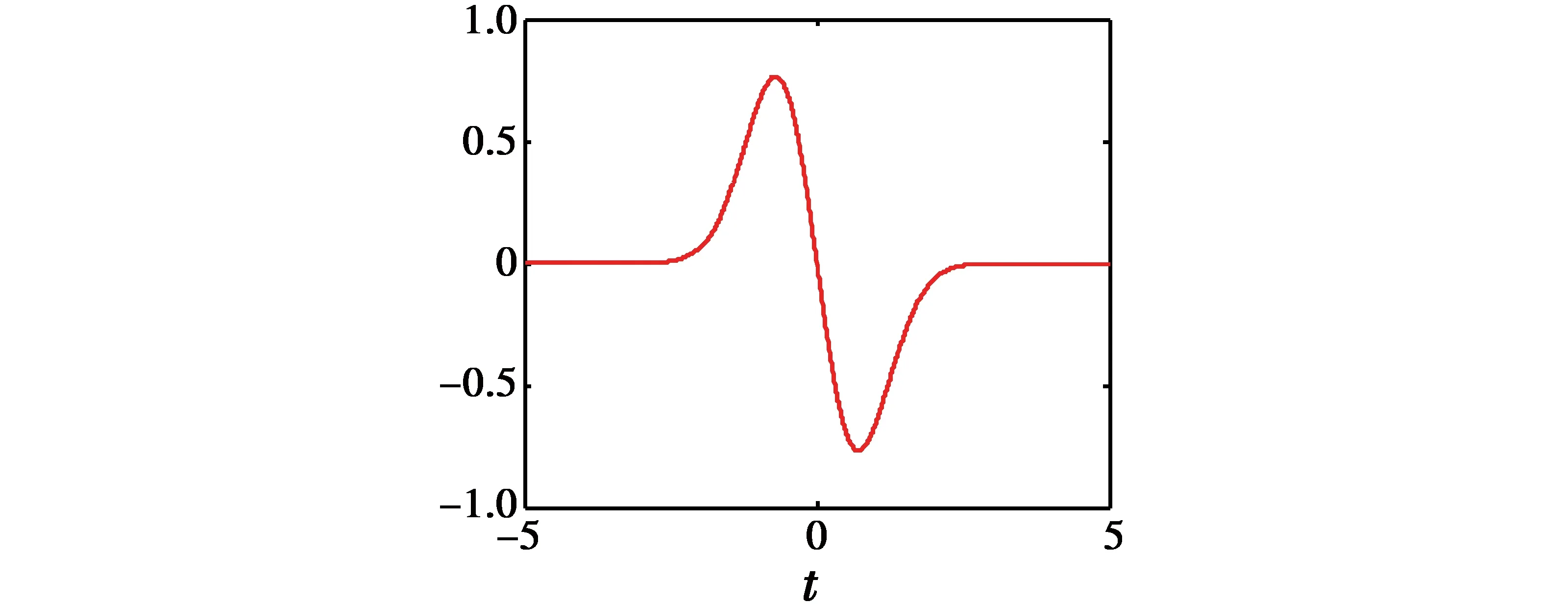
图2 高斯小波函数的函数曲线图Fig.2 The functional curve of Gaussian wavelet function
小波神经网络输出层计算式为
(2)
式中:k为输出层节点数目;l为隐含层节点数目。
3 GA-WNN评估模型的建立
3.1 遗传算法
遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法[13]。遗传算法是从代表问题潜在解集的一个种群开始,而一个种群则由经过基因编码的一定数目的个体组成。因此遗传算法的第一步就是编码操作,形成第一代种群,当第一代种群产生后,按照适者生存和优胜劣汰的原则,逐步淘汰适应度值差的解,得到越来越优的近似解。在每一代,根据适应度值选择个体,并且借助遗传算子进行交叉变异操作,生成代表新解集的种群。遗传算法包含选择、交叉、变异[14]3个操作。
1) 选择。选择是从当代种群中挑选出适应度值较好的个体,使其有机会作为父代种群产生新的种群。选择的依据是让适应度值好的个体有更大概率产生下一代个体。
2) 交叉。交叉通过组合父代种群个体的特性产生新的个体,将种群的各个个体随机搭配成对,以交叉概率交换它们之间的部分染色体。
3) 变异。对于种群的每一个个体,以变异概率改变一个或多个基因座上的基因值,形成新的个体,为了保持种群的相对稳定性,变异概率通常很小。
3.2 构建GA-WNN评估模型
GA-WNN评估模型就是利用遗传算法全局寻优能力强的特点,寻找最优初始的小波神经网络连接权值和伸缩平移尺度,避免了人为设定连接权值和伸缩平移尺度的盲目性[15]。因此,利用遗传算法优化小波神经网络能够提高整个网络的性能,使得优化后的小波神经网络的评估精度更高,得到更加符合实际的电子战无人机作战效能评估值。
1) GA-WNN评估模型结构的确定。
将前文分析所得的电子战无人机作战效能评估的6种影响因素(p1,p2,…,p6)作为输入向量,电子战无人机作战效能真实值T作为输出向量,由此可以确定GA-WNN的部分结构:输入层节点数为6,输出层节点数为1,隐含层节点数量通过试凑法确定。经过仿真实验,当隐含层节点数为10时表现出了最佳性能,于是本文就构建了一个6-10-1结构的单隐层GA-WNN评估模型。
2) GA-WNN评估模型的训练和评估。
GA-WNN评估模型的训练和评估过程如下所述。
① 种群编码。将小波神经网络的权值和伸缩平移参数(wi,ai,bi)进行编码,产生初代种群,其中,i为隐含层小波的个数。
② 遗传算法参数的设定。根据所设置的粒子的维数,最大进化次数为1000次,种群规模为50,其他参数采用系统默认。
③ 将初始的连接权值和伸缩平移参数(wi,ai,bi)赋给小波神经网络,然后根据适应度函数计算每个粒子的适应度值。根据需要,本文选用小波神经网络输出的相对误差和作为遗传算法的适应度值,则适应度函数为
(3)
④ 判断适应度值是否达到要求,如果达到要求,则将此时的连接权值和伸缩平移参数(wi,ai,bi)设置为最优参数,赋给小波神经网络,进行电子战无人机的作战效能评估。如果没有搜索到最佳的连接权值和伸缩平移参数(wi,ai,bi),则继续迭代寻优。
⑤ 选择2%适应度最大的个体, 直接继承给下一代,同时用父代适应度最大个体替代遗传操作后产生的最差个体。
⑥ 将前一代群体进行交叉和变异等遗传操作, 产生下一代群体,获取相应的连接权值和伸缩平移参数(wi,ai,bi),转到步骤③继续计算。
GA-WNN评估模型的训练流程如图3所示。

图3 GA-WNN训练流程图Fig.3 The flow chart of GA-WNN training
4 实际算例与分析
本文采用EINSTein系统[16]对电子战无人机的作战效能进行仿真,得出了基于EINSTein系统的仿真数据,并以此数据作为样本数据进行实例测试。本文共采集了1007组数据,其中,随机选取1000组样本作为神经网络的训练样本,剩余的7组样本作为测试样本。为了说明本文模型的有效性,采用Matlab2012a编程实现了本文所提出的基于遗传算法优化小波网络的模型。根据经验公式可得最佳隐含层节点数为3~13,本文分别对隐含层节点数为3,4,5,6,7,8,9,10,11,12,13的网络进行测试,结果表明结构为6-10-1的评估模型具有最好的训练效果。
为了证明GA-WNN有较高的评估精度,本文构建了用于和GA-WNN评估模型作对比的WNN评估模型和BPNN评估模型。使用相同的训练样本,分别对BPNN评估模型、WNN评估模型和GA-WNN评估模型进行训练,待训练结束后,分别向BPNN评估模型、WNN评估模型和GA-WNN评估模型输入测试样本,得到了BPNN模型输出评估值、WNN模型输出评估值、GA-WNN模型输出评估值与期望输出的对比曲线,如图4所示。

图4 评估结果示意图Fig.4 The schematic diagram of evaluation results
从图4中可以直观看出,相对于BPNN模型输出评估值和WNN模型输出评估值,GA-WNN模型输出值与期望输出的拟合程度更高,更能得到符合实际的评估结果。
本文将BPNN评估模型、WNN评估模型和GA-WNN评估模型的评估结果值分别与期望输出比较,得到了评估误差曲线如图5所示,相对误差曲线见图6。
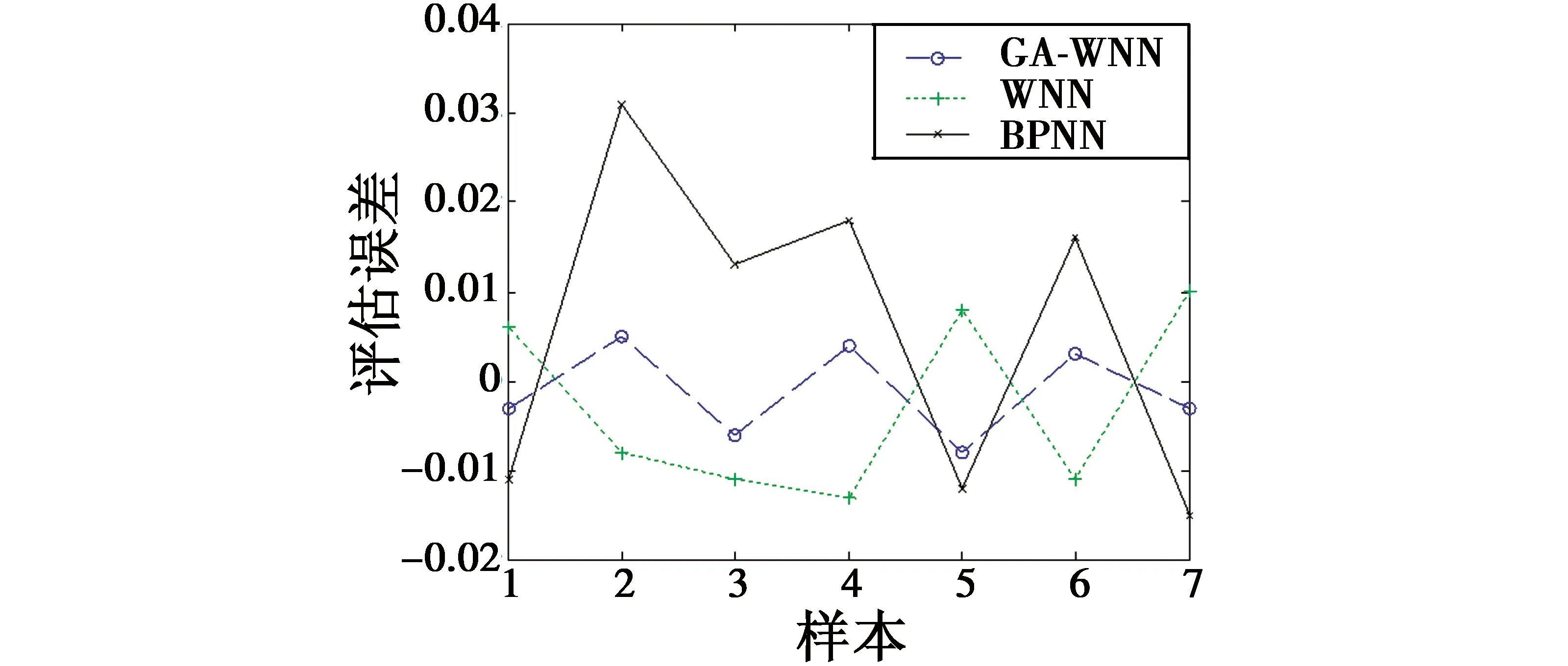
图5 评估误差示意图Fig.5 The schematic diagram of evaluation errors
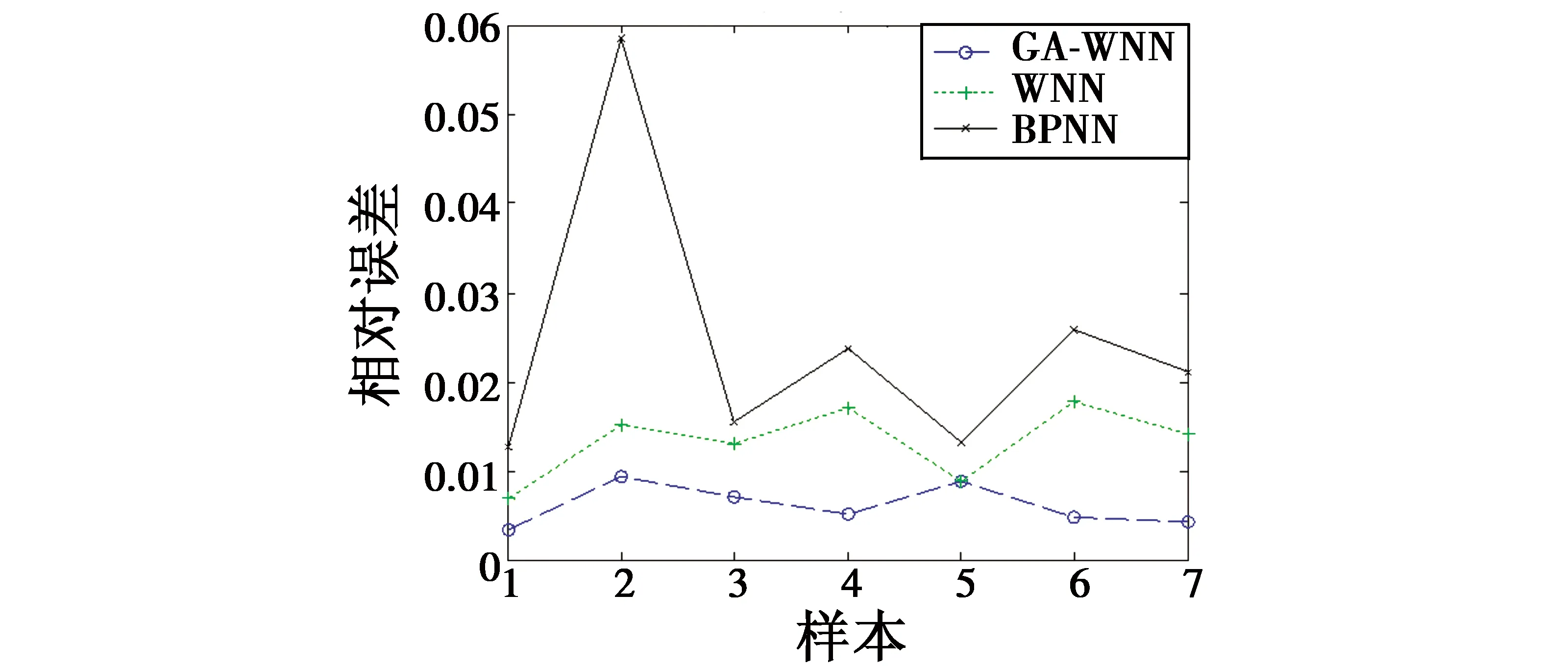
图6 相对误差Fig.6 Relative errors
从图5和图6中可以直观看出,GA-WNN评估模型的评估误差和相对误差相对稳定且趋向于0,反映GA-WNN评估模型对电子战无人机作战效能评估的可信程度更高。
经计算,GA-WNN评估模型评估结果的均方误差为0.000 168, WNN评估模型评估结果的均方误差为0.006 75,BPNN评估模型评估结果的均方误差为0.002 2。仿真结果表明: GA-WNN评估模型的评估精度高于WNN和BPNN,说明了GA-WNN评估模型可以作为今后电子战无人机作战效能评估的有效模型。
5 结束语
本文通过研究遗传算法优化小波神经网络的电子战无人机作战效能评估,构建了GA-WNN评估模型。通过实例证明相对于WNN评估模型和BPNN评估模型,该方法能够搜索到合理的权值和伸缩平移参数,使小波神经网络表现出了更加优异的性能,同时提高了神经网络的收敛速度和神经网络的评估精度,取得了很好的评估效果。因此,这种基于智能算法的评估模型可以解决复杂的非线性函数关系,拥有良好的学习能力和泛化能力,具有较高的实用价值。
参 考 文 献
[1] XUAN Y B,HUANG C Q,LI W X.Air combat situation assessment by gray fuzzy Bayesian network[J].Applied Mechanics and Materials,2011(69):114-119.
[2] LI Y N,HAN Z Z.Index and evaluation of radar anti-jamming ability based on improved grey correlation [J].Advanced Materials Research,2014(926-930):3629-3632.
[3] QI Z F,WANG G S.Effectiveness evaluation of electronic warfare command and control system based on grey AHP method [J].Journal of Chemical and Pharmaceutical Research,2014,6(7):535-542.
[4] GUO J,LI T W,LI C X,et al.Construction of shipborne navigation equipment’s comprehensive effectiveness evaluation index system based on improved ADC model[C]//IEEE Chinese Guidance,Navigation and Control Conference,2015:822-826.
[5] 陈浩光,李云芝,孙磊.基于模糊推理的武器系统效能评估新方法[J].军事运筹与系统工程,2004,18(4):63-68.
[6] 侯润民,刘荣忠,高强,等.粒子群小波神经网络在交流伺服系统中的应用[J].系统仿真学报,2014,26(4):881-885.
[7] 季彦婕,陈晓实,王炜,等.基于小波变换和粒子群小波神经网络组合模型的有效停车泊位短时预测[J].吉林大学学报:工学版,2016,46(2):399-403.
[8] 龙云, 贺新光, 章新平.月降水量预测的粒子群-小波神经网络模型[J].计算机科学,2015,42 (6A):138- 142.
[9] 毛红保,田松,晁爱农.无人机任务规划[M].北京:国防工业出版社,2015:188-195.
[10] 王东,张绍杰,尹晶,等.基于集成小波神经网络的卫星电源系统故障识别[J].电光与控制,2015,22(6):93-96.
[11] 王小川,史峰,郁磊,等.MATLAB神经网络43个案例分析[M].北京:北京航空航天大学出版社,2013:279-287.
[12] 王秋平,舒勤,黄宏光.含有误差校正的小波神经网络交通流量预测[J].计算机测量与控制,2016,24(2):168-170.
[13] 吴俊成,周锐,冉华明,等.遗传算法和拍卖算法在任务分配中的性能比较[J].电光与控制,2016,23(2):11-15.
[14] 金敏,鲁华祥.一种遗传算法与粒子群优化的多子群分层混合算法[J].控制理论与应用,2013,30(10):1231-1238.
[15] 李梦妍,于文震.基于改进小波神经网络和灰色模型的装备性能参数预测[J].电子测量技术,2016,39(3):18-22.
[16] 贺登高,吴志林.基于EINSTein的自适应指挥控制作战效能分析[J].火力指挥与控制,2013,38(1):87-90.

