一种改进CSA算法的UAV多任务区侦察决策问题研究

张耀中， 陈 岚， 张 蕾， 谢松岩

(西北工业大学电子信息学院，西安 710129)

0 引言

由于UAV具有较低的应用成本和较好的机动性，使其成为战场上被广泛使用的一种侦察手段。UAV可以在“危险、恶劣、枯燥”的任务环境中替代有人机执行战场侦察任务[1]。UAV任务侦察一般是指通过UAV所携带的任务载荷，来获取特定任务区域内情报信息的过程[2]。如何在UAV执行侦察任务前进行最优的任务规划，从而有效提高UAV的任务执行效率已经成为该领域中的一个研究热点问题，受到了诸多研究者的关注。如文献[3]在考虑三维任务环境和禁飞区限制的条件下，给出了一种基于改进的遗传算法求解方案来进行多UAV的路径规划，从而获得对目标区域的最大侦察信息;文献[4]提出了一种基于改进的自适应进化多目标优化算法来进行多UAV协同任务侦察，取得了良好的任务侦察效果。

通过分析大量的文献可以看出，目前研究者一般侧重于任务的航路规划和侦察搜救问题，大多未考虑UAV携带特定侦察载荷时的侦察信息收益最大化问题，该问题在很多应用场景中具有相应的实际意义。在高度复杂的战场环境中、震后的灾情分析中或大面积海域的海情侦察与搜索中，一般都有大量的热点区域需要UAV携带特定侦察载荷去执行信息收集任务。由于UAV所携带任务载荷的工作时间及能力都是有限的，通常难以完成对全部任务区的完全信息侦察，因此，如何能够快速有效地完成对所有任务区的非完全信息遍历侦察是本文的研究内容。本文提出一种将仿生智能算法——布谷鸟搜索算法[5-7]应用于UAV多任务区的协同侦察问题，很好地解决了对该类问题求解的快速性和有效性，从而为实际应用提供了决策依据[8-10]。

1 问题描述

在战场中的情报收集、震区灾情搜集与救援以及广域海上搜救等诸多任务中，经常需要单架UAV对任务区中多个感兴趣的区域进行信息侦察。由于UAV的性能、携带载荷的有效工作时间及载荷的工作能力都是受限的，如何规划出最优的任务路径，同时规划出载荷在各个感兴趣区域的工作时间对整个侦察任务的完成效果都有极大的影响[11-12]。设定任务场景中存在N个感兴趣的待侦察区域，如图1所示。

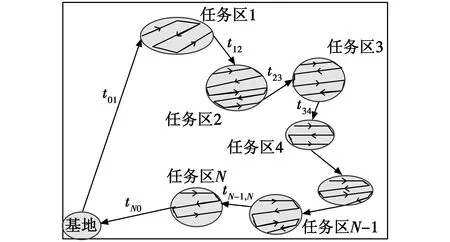
图1 UAV多任务区侦察规划示意图Fig.1 Reconnaissance planning of UAV multi-task area

图中，tij表示从任务区i到任务区j的任务飞行时间，其中，i=0时表示基地。假定N个待侦察任务区的位置、范围及所需任务载荷均为已知，则对任务区的侦察信息收益就主要体现在UAV所获取的侦察情报，通常侦察情报的获得主要由UAV在该任务区内载荷的工作时间决定，载荷工作时间越长，所获得的对该任务区的情报信息就越多。通过研究，本文引入对任务区的侦察信息确定性指标来度量任务载荷的侦察信息收益，通常在UAV进入预定任务区之前对该任务区的先验情报信息为0，随着侦察载荷工作时间的增加，对该任务区的信息确定性度量值将逐渐增加，当该任务区的信息确定性指标接近1时就完成对该任务区的完全信息侦察。通常UAV在侦察过程中由于续航时间及载荷持续工作时间等的约束，难以完成对全部任务区的完全信息侦察，通常也没有必要进行完全信息侦察。因此，如何在满足相应约束条件下使UAV对所有待侦察任务区综合侦察信息确定性指标达到最大化是本文要解决的问题。

2 布谷鸟搜索算法(CSA)

在UAV执行对多任务区的侦察问题中，对感兴趣任务区的传感器工作时间分配问题属于连续时间约束的非线性规划问题，是典型的NP Hard问题。由英国剑桥大学YANG等提出的布谷鸟搜索算法(Cuckoo Search Algorithm,CSA)在解决该类问题时表现出了较好的计算性能，因此，选择CSA进行相应的改进来求解该问题。

2.1 CSA介绍

CSA主要是基于北美一种布谷鸟的寄生孵化行为，并采用Lévy飞行的随机游走进化策略[5]来进行最优解的获取。该算法设计了3条基本规则:1) 每只布谷鸟每次只能产下一枚蛋，同时布谷鸟随机地选取一个其他种类的鸟巢进行寄生孵化;2) 具有最优性能的鸟巢会被保存到进化过程的下一代;3) 用来寄生孵化的鸟巢数目固定，设宿主鸟发现外来鸟蛋的概率为pa,假如宿主鸟发现了外来鸟蛋，则宿主鸟或抛弃这个蛋，或抛弃该鸟巢，并寻找新的位置重建鸟巢。该进化算法操作简单，只需设置鸟巢数量n和宿主鸟发现外来鸟蛋概率pa两个参数。

CSA的进化过程主要包括最优鸟巢的选择、局部随机扰动、全局Lévy飞行随机选择3个过程[7]。

1) 最优巢穴的选择。在算法迭代过程中，保留当前代中性能最好的巢穴直接进入下一代种群中，以保证算法的迭代性能，类似于遗传算法中的精英保留主义。

2) CSA的局部随机扰动。算法进化过程中叠加随机扰动，保证种群的多样性。局部随机扰动过程为

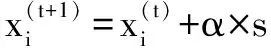
(1)

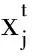
3) 采用Lévy飞行过程进行算法迭代。

算法的迭代进化过程采用全局Lévy飞行随机游走策略进行，即

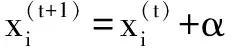
(2)

式中:

(3)

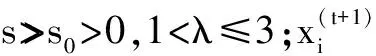
2.2 CSA的基本处理流程

CSA的基本处理流程如图2所示。

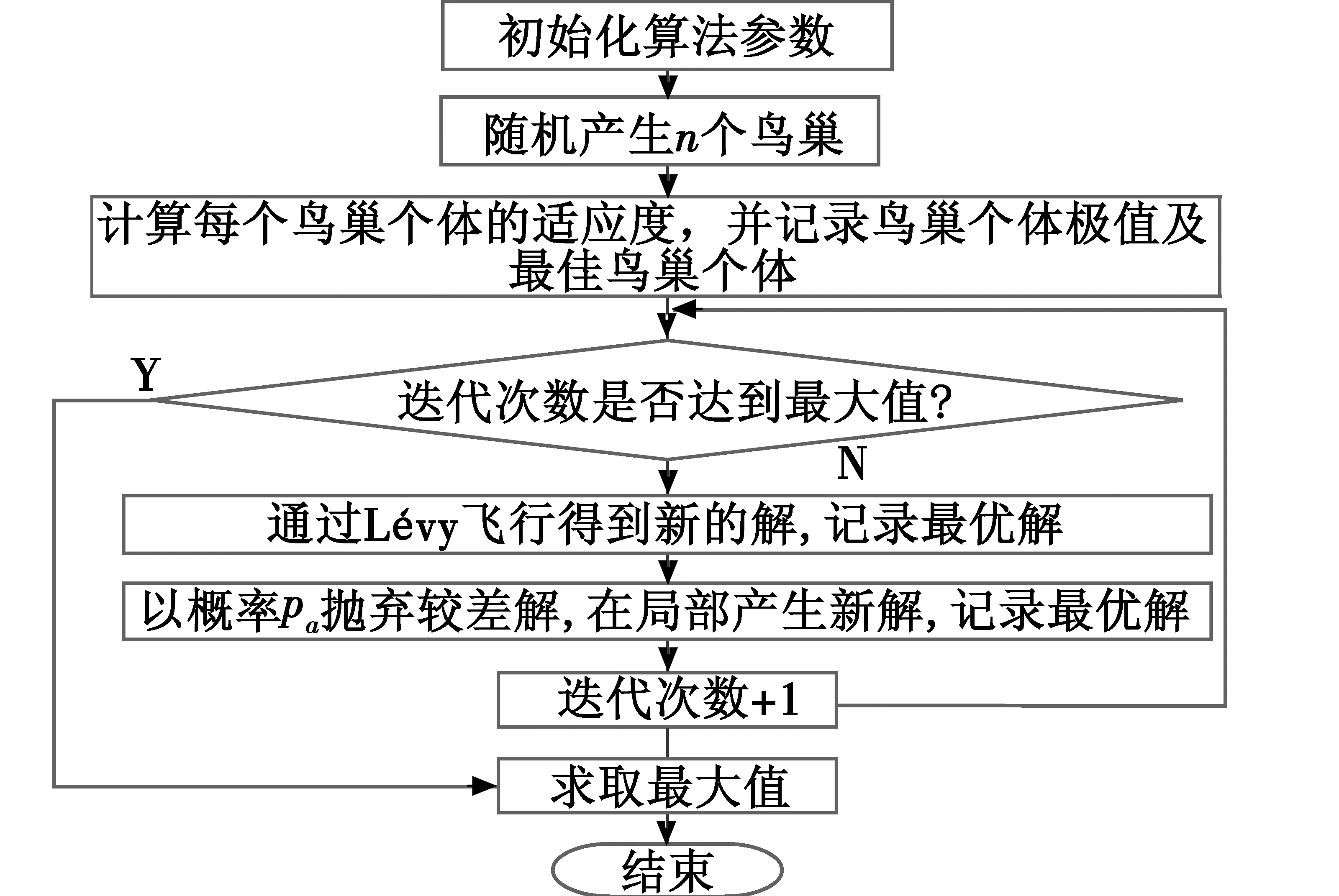
图2 CSA流程图Fig.2 Flow chart of CSA

2.3 CSA的离散化方案

CSA在解决连续变量最优化问题中显示出良好性能，但是标准的CSA只能求解具有连续型变量的最优化问题，无法求解离散型变量的最优化问题[13-14]。在本文中采用一种基于Lévy随机分布策略的插入、交换、倒置操作算子来进行算法的离散化，从而求解最优侦察路径规划问题。离散布谷鸟搜索算法处理流程见图3。

图3 离散布谷鸟搜索算法流程图Fig.3 Flow chart of discrete CSA

2.4 CSA的改进策略

基本型的CSA进化过程具有较大的随机性、迭代过程难以控制，收敛速度难以保证[15]。因此，本文基于基本型的CSA和侦察决策问题的特点，给出对应的改进措施，提出一种改进型CSA(ICSA)，包括采用自适应步长的比例调节因子、进化过程中解向量的高斯扰动法则。

1) 自适应步长比例调节因子

(4)

2) 解向量的高斯扰动法则。

CSA的特点就是参数少、全局搜索能力较强、局部搜索能力较弱，因此在进化迭代过程中，采用对解向量进行小步长的扰动，使鸟巢进化位置进行微调以增加解向量的多样性，不仅加快了收敛速度，而且有效提高了算法的局部搜索性能[16-17]。

引入解向量的高斯扰动，当CSA经过Lévy飞行得到一组新的解向量后，通过增加一次高斯扰动，使得新的解向量在旧的解向量附近微调并保留较优的解向量。该过程可表示为

xn*=xn+k⊕u

(5)

式中：x为鸟巢的位置向量；u为与解向量同阶的随机矩阵且满足uij～N(0,1)；k为扰动调节因子，避免对解向量造成的影响过大而导致算法的进化效率下降。

3 UAV多任务区侦察决策问题的建模

为了叙述方便，定义：n为仿真任务场景中的待侦察任务区数量；M为UAV基地与待侦察任务区集合,M={1,2,3,…,n},节点{1}为基地，节点M{1}为待侦察任务区的集合；E表示待侦察任务区之间的任务路径，E={i,j|i,j∈M,i≠j}；(xi,yi)为第i个任务区中心点的位置坐标，i∈M，(x1=0,y1=0)；Si为第i个任务区的待侦察面积，i∈M，设定任务区为长方形规则区域；dij为第i个任务区到第j个任务区的距离；Dmin为从基地起飞完成对所有任务区遍历飞行的最短任务航路；ci为第i个任务区的侦察价值，i∈M；w为所携带侦察载荷的扫描宽度；v为UAV的飞行速度；T为UAV的总任务可飞行时间；tij为UAV从任务区i到任务区j的飞行时间，tij=dij/v；tmin为UAV从基地起飞完成任务航路飞行所需的最小飞行时间；Gimin为第i个任务区需要达到的最小信息侦察收益，i∈M；Gi为对第i个任务区的侦察信息收益；Gmax为对全部任务区进行侦察所获取的综合化最大侦察信息收益；ti为第i个任务区分配的载荷工作时间，

3.1 多任务区侦察决策问题的解决方案

在多任务区的侦察决策问题中，需要解算的决策变量有Xij和ti两类。为了使每个任务区都能获取到比较满意的侦察信息收益，首先需要保证UAV对全部待侦察任务区的侦察路径是最优的，从而保证有更多的有效任务工作时间分配给相应的任务区来执行相应的侦察任务。在此将整个任务决策过程分为2个阶段来求解:第1阶段主要进行侦察路径的规划，求取UAV完成所有任务区飞行所需要的时间;第2阶段进行任务区侦察时间的分配，将UAV剩余的可用任务飞行时间最优化地分配给相应的任务区。两阶段的求解过程见图4。

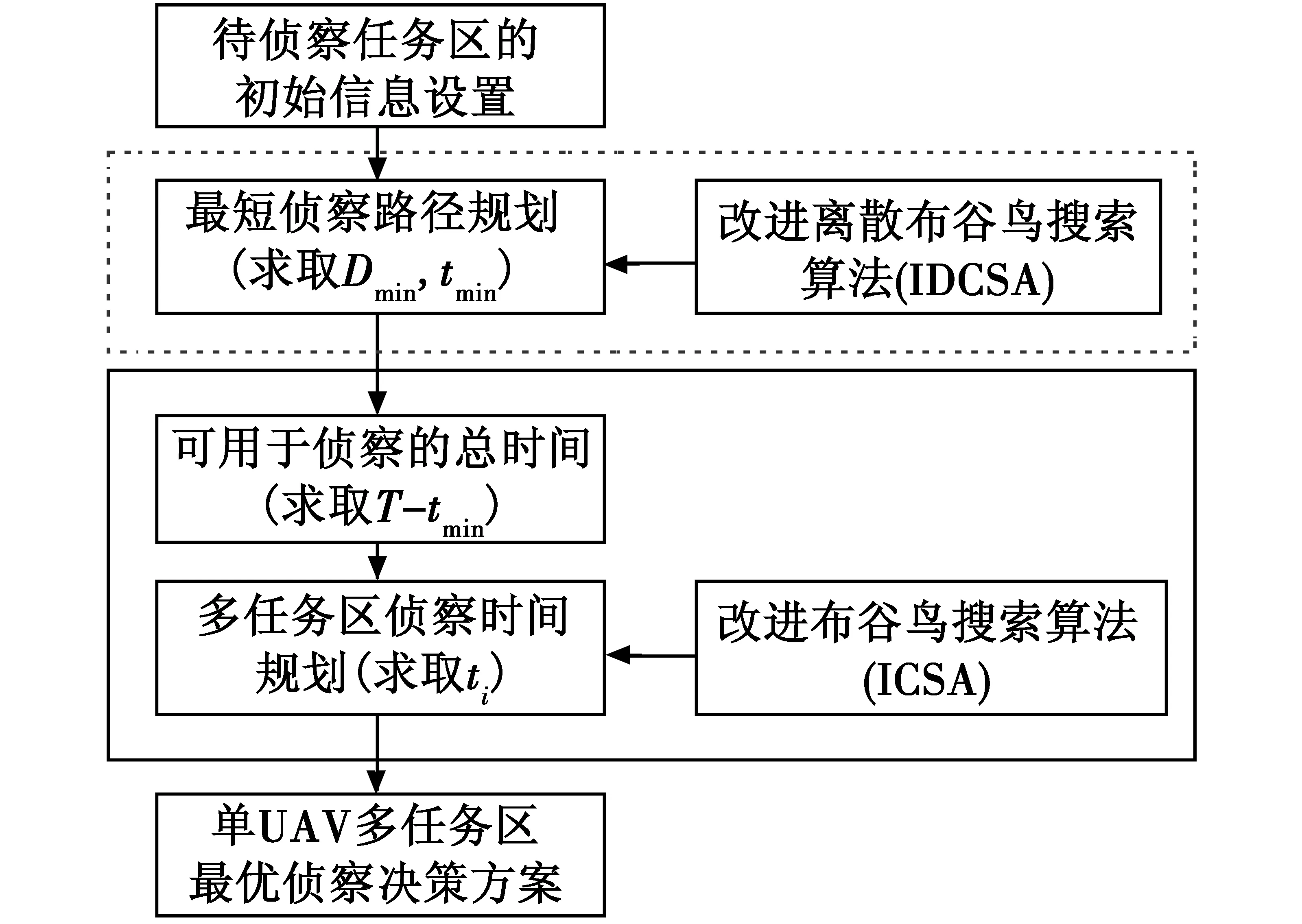
图4 多任务区侦察决策问题求解流程Fig.4 Process of multi-task area reconnaissancedecision-making

3.2 UAV最短侦察路径规划模型

UAV对多任务区进行侦察的最短任务路径问题可以归结为经典的TSP问题来进行求解，建立数学模型为

(6)

(7)

约束条件为

(8)

(9)

(10)

(11)

(12)

(13)

其中：约束方程式(8)、式(9)为任务区的侦察约束，确保每个任务区只能到达一次;约束方程式(10)为侦察遍历约束，保证UAV能够遍历飞行到所有待侦察的任务区；约束方程式(11)为起点约束，保证UAV从基地起飞；约束方程式(12)为终点约束，保证UAV完成任务后能够返回基地；约束方程式(13)为平衡约束。

3.3 UAV对任务区的侦察信息度量指标

UAV对任务区进行任务侦察的主要目的是获取有用的情报信息，降低决策者对相应任务区的不确定性，一般而言，UAV对任务区进行侦察时都处于极其复杂的外部环境，难以保证对每个任务区都能够进行完全信息侦察。UAV的侦察信息收益主要取决于其所携带的侦察载荷的工作能力，在特定侦察载荷(如机载CCD照相设备等)下，UAV在每个待侦察任务区内的侦察信息收益主要与在该任务区内的载荷工作时间成正比，载荷工作时间越长，侦察收益越大。因此，侦察信息的度量主要与UAV在该任务区内的侦察时间长短、所携带侦察载荷的工作能力等因素相关，即

G(t)=G0+G1(1-e-βt)

(14)

式中：G0为侦察任务开始前UAV对该任务区域的已知信息，0≤G0<1，G1为UAV对任务区的信息不确定性部分，且G0+G1=1;β为侦察载荷对任务区的侦察能力指数。不同侦察载荷的工作能力指数对侦察收益的影响如图5所示。

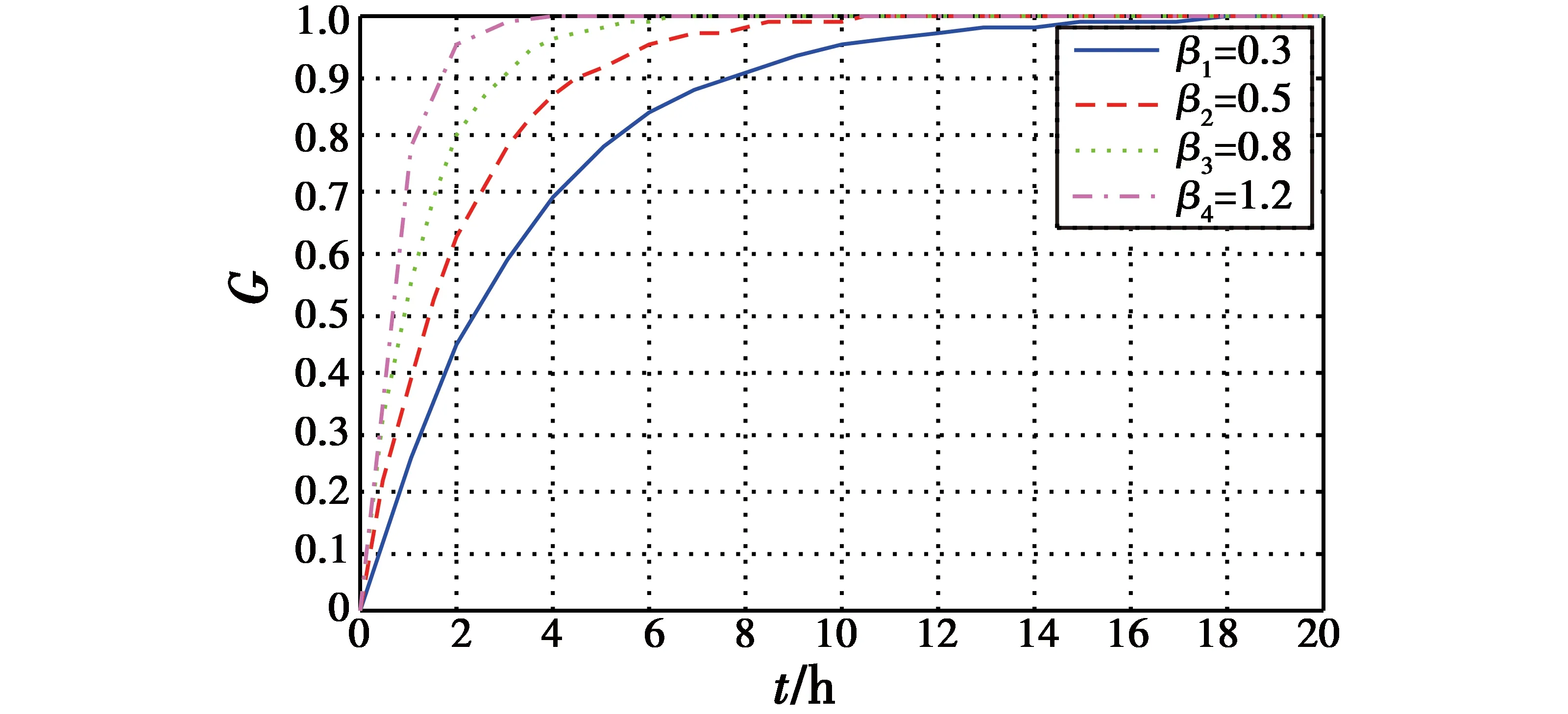
图5 不同侦察载荷工作能力下的侦察收益曲线Fig.5 Reconnaissance revenue curve under different reconnaissance load capacity

为便于计算，假定UAV在对任务区进行侦察前没有任何已知信息，即取G0=0。同时设定任务区为矩形区域，侦察载荷为机载CCD照相设备，则侦察能力指数主要由任务区的面积S，侦察载荷的有效扫描宽度w及UAV的任务飞行速度v所决定，表示为

(15)

则UAV侦察收益的信息确定性度量指标可以表示为

G(t)=1-e(-w·v/S)t。

(16)

3.4 UAV多任务区侦察信息收益模型

多任务区的侦察时间分配问题可以表示为如下的最优化问题，即

(17)

式中，ci为任务区的价值系数。

该最优化问题的约束条件为

(18)

tmin=Dmin/v

(19)

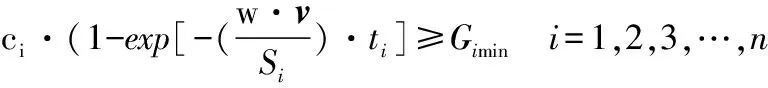
(20)

其中：约束方程式(18)为UAV对所有任务区的任务飞行时间约束；约束方程式(20)为每个任务区需要满足的最小侦察收益约束。

4 仿真实验

以某侦察UAV为参考，在Windows7操作系统和Matlab2012b 编程环境下进行仿真验证。设定UAV的最大任务工作时间为30 h，任务飞行速度为v=220 km/h，所携带侦察载荷的有效扫描宽度为w=0.3 km，以UAV所在基地坐标为原点建立坐标系，场景中感兴趣的任务区域共有24个，任务区域的有关参数如表1所示。

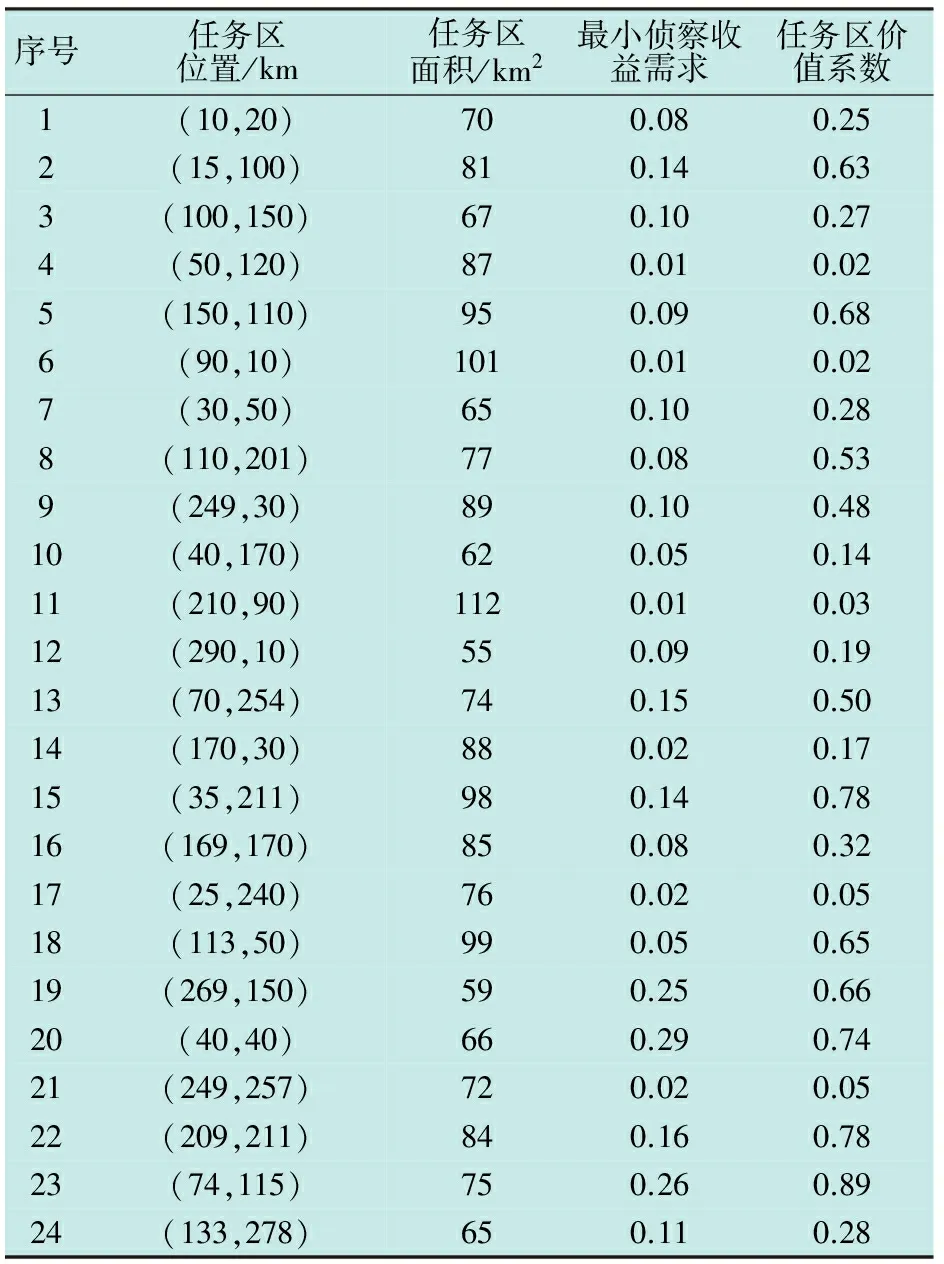
表1 待侦察任务区域的信息设置表

基于上述仿真任务想定，将问题划分为任务航路规划和任务区侦察时间分配两个阶段，分别采用离散型和连续型的ICSA进行求解。

仿真中设定ICSA的最大迭代次数为500，巢穴的数量为20，宿主鸟发现外来鸟蛋的概率为0.25，对每个待侦察任务区的侦察时间分配及相应的侦察信息收益及侦察任务航路规划结果分别如图6、图7所示，其中,i为对应任务区序号，UAV完成全部任务区侦察的总侦察信息收益为6.12，从UAV所在基地起飞遍历全部任务区的最小任务航路飞行时间为6.62 h，任务航路的飞行距离为1 456.33 km。

为了分析ICSA的收敛速度，针对以上仿真任务场景分别选用了基本CSA和GA进行了对比计算，3种算法的进化收敛曲线如图8所示。

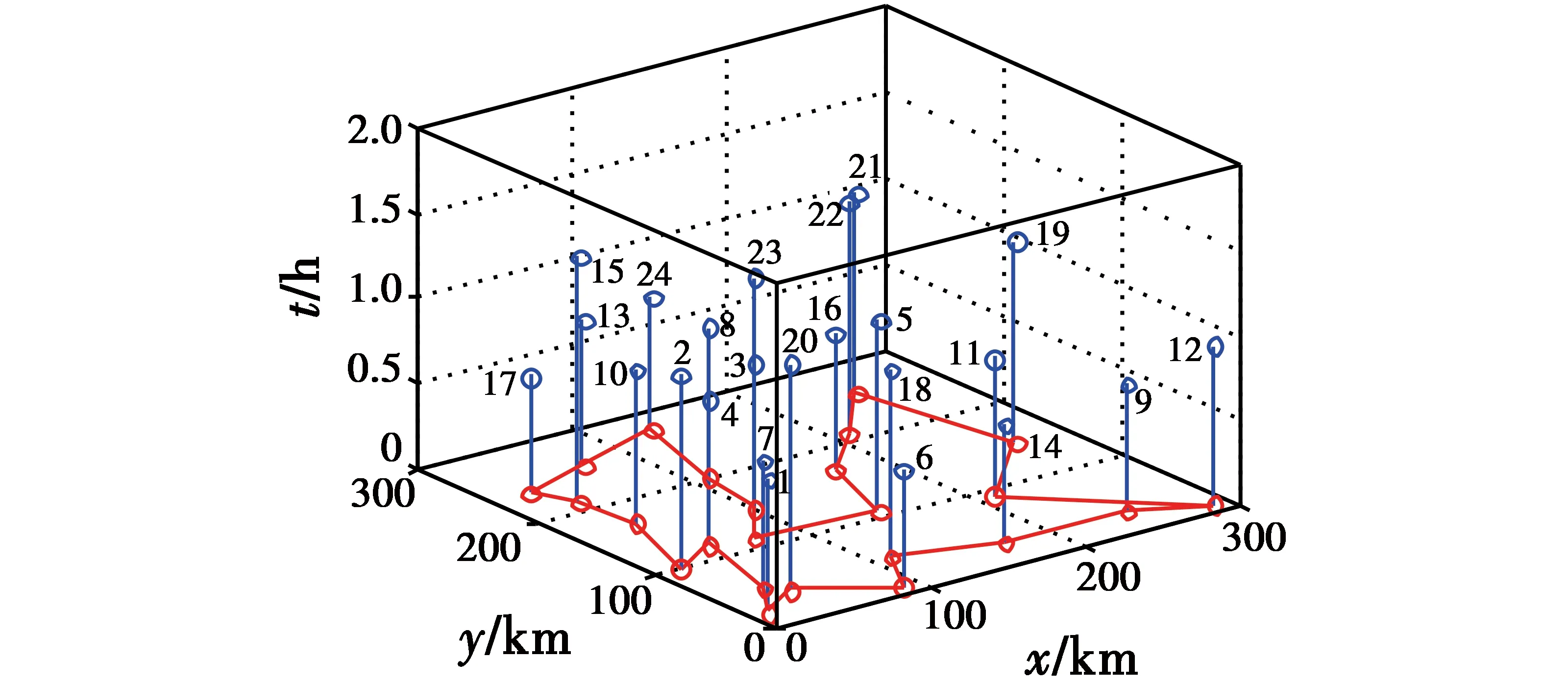
图6 UAV多任务区侦察时间分配结果图Fig.6 Time allocation result of multi-task area reconnaissance

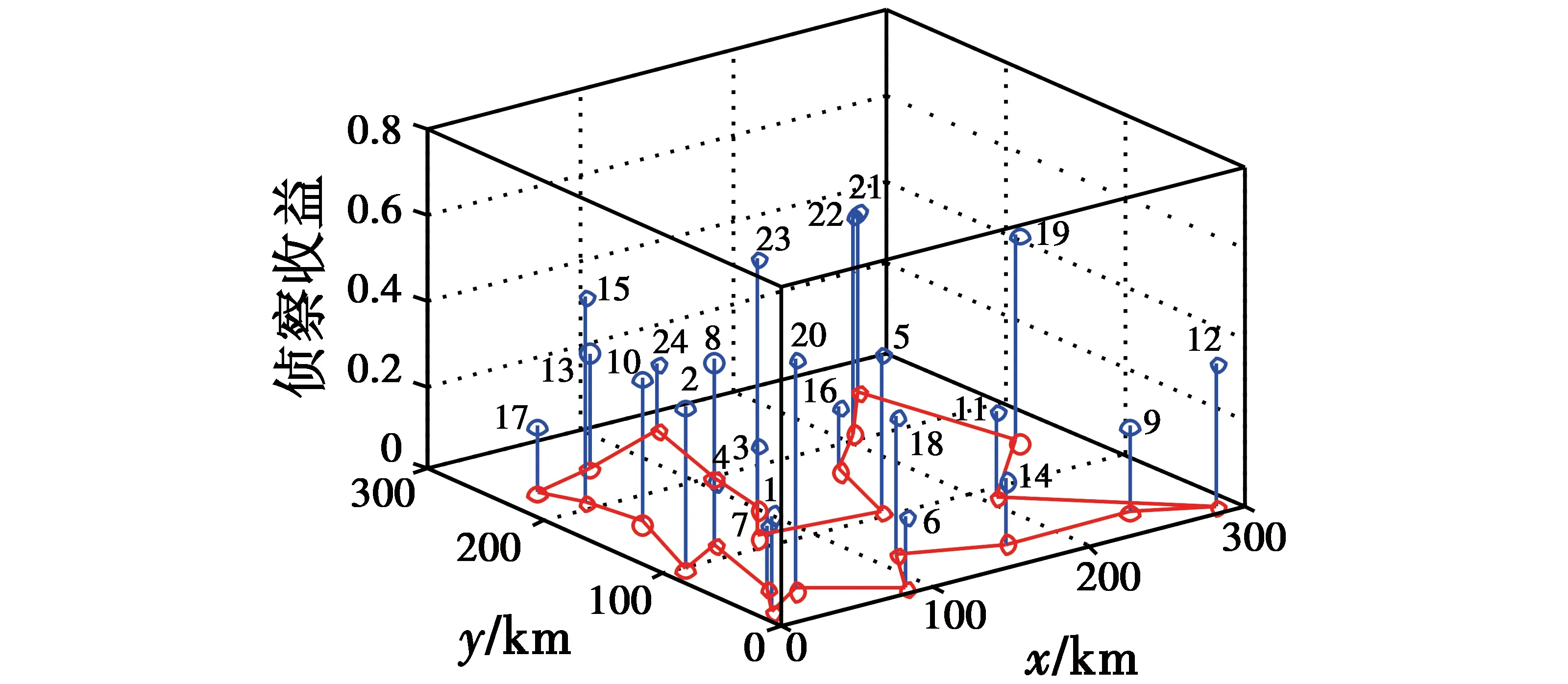
图7 UAV多任务区侦察收益图Fig.7 Revenue of multi-task area reconnaissance

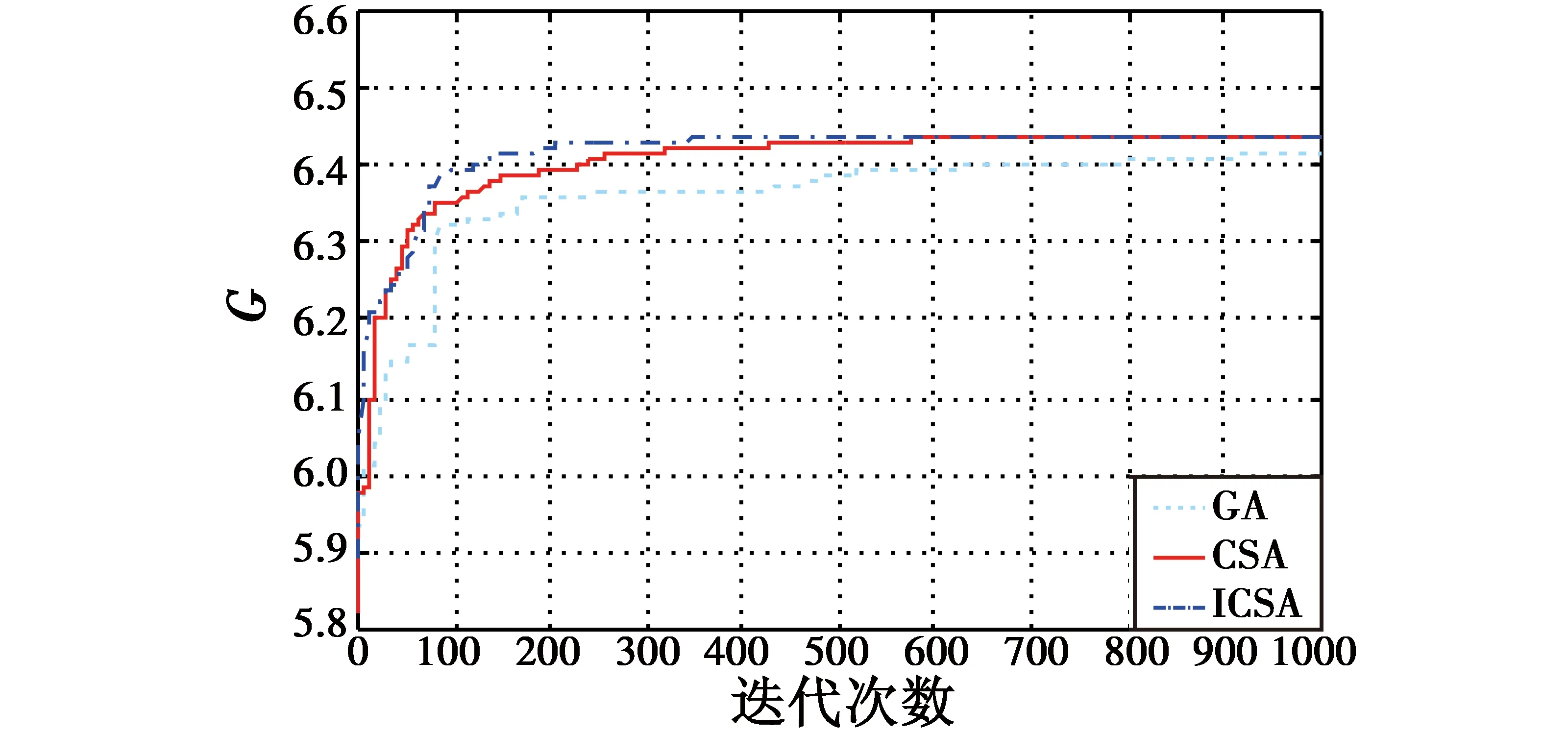
图8 ICSA,CSA,GA算法下的进化收敛曲线Fig.8 Evolution curve of ICSA,CSA and GA

仿真结果显示,GA运行时间为19.20 s，而ICSA运行时间仅为6.07 s，可见ICSA求解速度明显快于GA。从ICSA,CSA和GA这3种的进化收敛曲线能够看出，相比于标准CSA和GA，ICSA能够克服GA早熟的缺点，收敛速度快，同时自适应的搜索步长能够明显提高基本CSA进化的速度，从而能够在较小的迭代次数下快速收敛。仿真计算结果表明,ICSA能够快速有效地给出多任务区侦察决策问题的最优方案。

5 结论

本文针对UAV多任务区的侦察决策问题，将整个侦察决策过程分为任务路径规划与侦察时间分配2个阶段，给出了侦察信息的度量指标。同时提出了一种改进的CSA为每个待侦察任务区分配最优的任务侦察时间，从而使整个侦察任务过程的信息收益最大化。最后进行了相应的仿真分析，仿真结果表明，该算法可以在UAV任务飞行时间约束下获得对多任务区的综合侦察信息收益最大化决策方案。

参 考 文 献

[1] LOH R,BIAN Y,ROE T.UAVs in civil airspace:safety requirements[J].IEEE Aerospace and Electronic Systems Magazine,2009,24(1):5-17.

[2] 许友平.无人机对地侦察/攻击航路规划软件系统的研制与研发[D].南京：南京航空航天大学,2013.

[3] ERGEZER H,LEBLEBICIOLU M K.3D path planning for UAVs for maximum information collection[C]//International Conference on Unmanned Aircraft Systems(ICUAS),2013:79-88.

[4] MA J Y,ZHANG K H.Research on TSP solution based on genetic algorithm of logistic equation[C]//The 2nd International Conference on Computer Science and Network Technology,2010:738-742.

[5] YANG X S,DEB S.Cuckoo search via Lévy flights[C]// World Congress on Nature & Biologically Inspired Computing(NaBIC 2009),2010:210-214.

[6] YANG X S.Cuckoo search and firefly algorithm[M].Poland:Polish Academy of Sciences,2014:49-195.

[7] YANG X S,DEB S.Engineering optimization by cuckoo search[J].International Journal of Mathematical Modelling and Numerical Optimisation,2010,1(4):330-343.

[8] 张耀中,胡波，李寄玮，等.不确定环境下无人机多任务区侦察决策研究[J].西北工业大学学报，2016，34(6)：1028-1034.

[9] BAXTER J,FINDLAY S,PAXTON M.Scheduling UAV surveillance tasks,lessons learnt from trials with users[C]//IEEE International Conference on Systems,Man and Cybernetics,2013:2606-2610.

[10] SHIN H S,LEBOUCHER C,TSOURDOS A.Resource allocation with cooperative path planning for multiple UAVs[C]//UKACC International Conference on Control, 2012:298-303.

[11] HABIB D,KHAN S A,JAMAL H. Collaborative path planning for multiple unmanned aerial vehicles in dynamic environment[C]//The Signal Processing, Communications and Computing (ICSPCC),2011:1-5.

[12] BERTUCCELLI L F,CHOI H L,CHO P,et al.Real-time multi-UAV task assignment in dynamic and uncertain environment[C]//AIAA Guidance,Navigation,and Control Conference,2009:10-13.

[13] YANG X S,DEB S.Cuckoo search:recent advances and applications[J].Neural Computing and Applications, 2014,24(1):169-174.

[14] OUAARAB A,AHIOD B,YANG X S.Discrete cuckoo search algorithm for the traveling salesman problem[J].Neural Computing and Applications,2014,24(7/8):1659-1669.

[15] OUAARAB A,AHIOD B,YANG X S,et al.Discrete cuckoo search algorithm for job shop scheduling problem[C]//IEEE International Symposium on Intelligence Control(ISIC),2014:1872-1876.

[16] MARICHELVAM M K,PRABAHARAH T,YANG X S.Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan[J].Applied Soft Computing,2014,19(1):93-101.

[17] YANG X S,DEB S.Multiobjective cuckoo search algorithm for design optimization[J].Computers & Operations Research,2013,40(6):1616-1624.