求解广义正则长波方程的新型守恒差分方法
陈佳欣, 邵新慧
(1. 辽宁石油化工大学 理学院, 辽宁 抚顺 113001; 2. 东北大学 理学院, 辽宁 沈阳 110819)
考虑如下一类广义正则长波(GRLW)方程的初边值问题:
此问题具有如下守恒律:

(4)
其中C为一般正常数,由于方程的物理边界满足当|x|→∞时,u→0,方程单个孤波解为

(5)

σ和x0是任意常数(p≥2).当-xL,xR充分大时,初边值问题与方程的柯西问题是一致的.
对广义正则长波进行研究,当p=2时,此方程为正则长波方程,正则化长波(RLW)方程是一个重要的非线性波动方程,在非线性色散介质中传播[1-4].其中广义正则长波方程在物理介质中扮演着非常重要的作用,因为它描述了许多非线性现象,包括在浅水中含有非线性横波的色散波、等离子体中的离子声和磁流体波.因此广义正则长波方程理论的研究具有重要的意义[5-7],尤其是它所描述的运动有与KDV方程相同的逼近界,也能很好地模拟KDV的几乎所有应用.关于广义正则长波方程的研究较为普遍,但是KDV方程在求解过程中少有解析解,所以讨论方程的数值解法十分有意义.
针对广义正则长波方程(GRLW)建立一种新型的保守差分格式.对于广义正则长波方程过程(GRLW),多数是采用数值解法,Chen研究了广义对称正则长波方程孤立波解的轨道稳定性与不稳定性[8];Bona通过Fourier谱方法对GRLW方程的初边值问题进行了研究[9];Dogan针对长波方程提出了Galerkin求解方法[10];Tian等人借助计算机计算,使用广义双曲函数方法获得(2+1)维对称正则化长波方程的精确解析解[11];Kaya考虑广义正则长波方程的孤立波解解决方案,该文求得了广义正则长波方程的确切孤立波解,并通过使用Adomian分解方法而不是传统方法求出了广义正则长波方程的数值解[12];Soliman为了解决广义正则长波方程数值解问题,使用了变分迭代法[13];Cai在求解正则长波方程过程中使用新的六点多辛和十点显式多辛2个格式[14];Mohammadi等人为了解决GRLW方程的数值解,在研究中运用正弦基函数的无网格技术.此外,他们提出了一个新的迭代算法解决GRLW方程[15];徐友才等人提出了广义正则长波方程的一个两层非线性守恒差分格式[16];胡劲松提出了拟紧致守恒差分格式[17].这些研究成果的出现,使广义正则长波方程数值解法的研究变得系统化和理论化,为后续研究提供了充足的理论保障和实践经验.
对于徐友才对问题(1)~(3)提出了具有二阶精确度的两层守恒格式[16],但是方程中的非线性项(up)离散太过复杂,当参数p较大时,由于每项打开分别求和,此格式计算耗时很大.胡劲松提出了一个两层拟紧致守恒差分格式[17],虽然差分格式较为简单,但结果的精度一般.为此,本文构造了一个新的差分格式,此格式为一个带有权系数的3层差分格式,3层差分格式比徐友才提出格式更为简单,新格式合理地模拟了守恒量,从而适合长时间计算,当θ取不同值时,精度会发生变化,数值算例表明,相对于胡劲松提出的2层二阶格式,该格式的精度有了提高.
1 预备知识及相关引理
广义正则长波方程作为非线性偏微分方程的一种,通常被用来解释很多科学分支和物理现象.但是求解偏微分方程的解析解非常困难,所以讨论方程的数值解法十分有意义[18-19].
有限差分法作为求解偏微分方程的主要数值方法,由于数字电子计算机只能存储有限个数据和做有限次运算,所以任何一种用计算机解题的方法,都必须把连续问题离散化,最终化成有限形式的线性代数方程组.用差分法将连续问题离散化的步骤是,首先对求解区域作网格剖分,用有限个网格节点代替连续区域;其次将微分算子离散化,从而把微分方程的定解问题化为线性代数方程组的求解问题[20].
差分法的基本问题有:
(1) 对求解域作网格剖分.一维情形是把区间分成一些等距或不等距的小区间,称之为单元.二维情形则把区域分割成一些均匀或不均匀的矩形,其边与坐标轴平行,也可分割成一些三角形或凸四边形等[20].
(2) 构造逼近微分方程定解问题的差分格式.
(3) 差分解的存在唯一性、收敛性及稳定性的研究.这些理论问题都归纳到对差分解作出先验估计.
(4) 差分方程的解法.
作为模型,考虑一维热传导方程
(6)
其中,a是正常数,f(x)是给定的连续函数按照定解条件的不同给法,可将式(6)的定解问题分为2类:
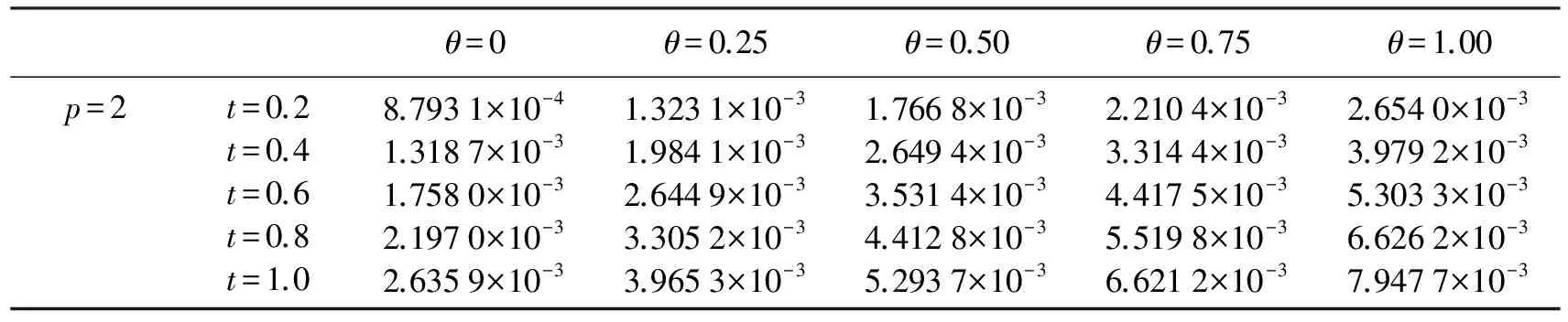
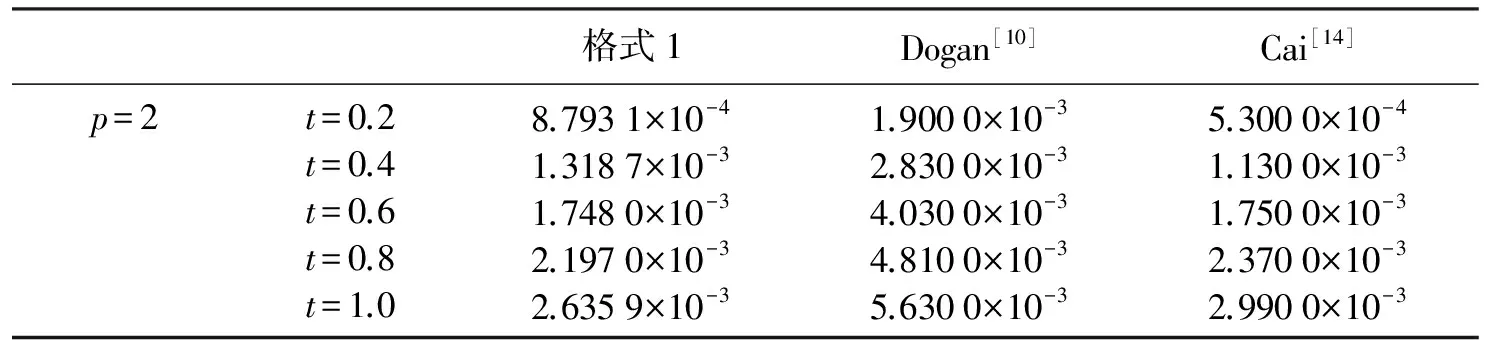
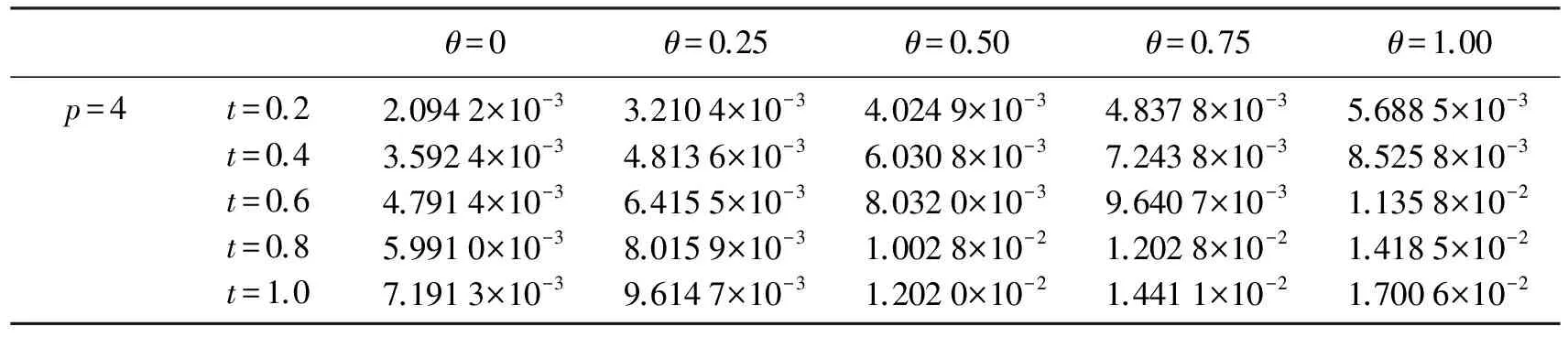
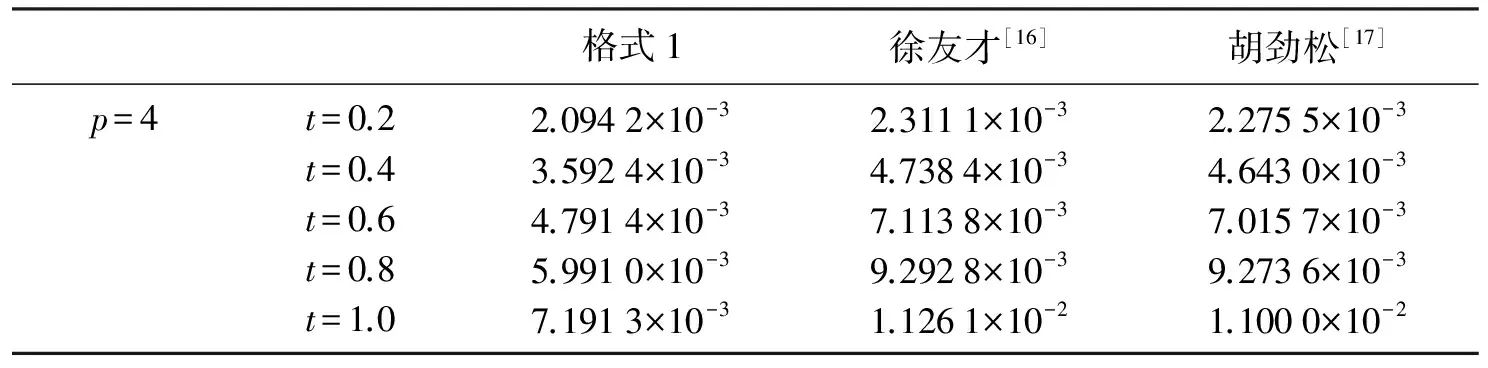
第1类 初值问题(也称Cauchy问题):求具有所需次数偏微商的函数u(x,t),满足方程(6)(-∞ u(x,0)=φ(x),-∞ (7) 第2类 初边值问题(也称混合问题):求具有所需次数偏微商的函数u(x,t),满足方程(6)(0 u(x,0)=φ(x),0 (8) 及边值条件 u(0,t)=u(l,t)=0,0≤t≤T. (9) 假定φ(x)在相应区域光滑,并且在x=0,l与边值相容,使上述问题有唯一充分光滑的解. (1) 向前差分格式[21],即 其中,j=1,2,…,N-1,k=1,2,…M-1.以r=aτ/h2表示网比,将式(10)改写成便于计算的形式,使第k层值在等式右边,第k+1层值在等式左边,则得 (12) 由于第(k+1)层值通过第k层值表成为(12)无需求解线性代数方程组,如此的差分格式称为显格式. 截断误差为O(τ+h2),其增长因子为 (13) (2) 向后差分格式,即 其中,j=1,2,…,N-1,k=1,2,…,M-1.将式(14)改写为 (16) 由于第(k+1)层值不能用第k层值明显表示,而是由线性代数方程组(16)确定,如此的差分格式称为隐格式. 截断误差为O(τ+h2),其增长因子为 (17) (3) Crank-Nicolson格式(CN格式)为 截断误差为O(τ2+h2),其增长因子为 (19) 差分格式稳定性分析的方法有Fourier级数法、矩阵分析法和能量法. (1) Fourier级数法 考虑下面实直线R上的一个初值问题 定义u关于x的空间Fourier变换为 逆Fourier变换为 假定偏微分方程的解在±∞处足够好,使得积分存在且在±∞处为零.Fourier变换的一个性质是Parseval等式,即 Parseval等式表示函数的模与其变换后的模在各自的空间中相等. 为分析关于初边值问题差分格式的稳定性,需要考虑离散Fourier变换.假定在实或复l2空间中给定向量u=(…,u-1,u0,u1,…)T.定义 若特别强调空间离散步长的影响,可定义 (2) 矩阵分析法 命题2[22]对如下形式的两层格式 un+1=Qun,n≥0,(n+1)Δt≤T, (20) 差分格式(20)关于模‖·‖是稳定的当且仅当存在正常数Δx0和Δt0以及非负常数K使得 ‖Qn+1‖≤K (21) 对0<Δx≤Δx0,0<Δt≤t0成立. 上面介绍了初边值问题稳定性分析的Fourier级数法,对初边值问题,还可以用矩阵法来进行分析.初边值问题的差分格式可以写成下面的形式 un+1=Qun. (22) 如果是隐式格式 Q1un+1=Q2un 则可变成 这仍然是式(22)的形式.根据命题2,为了讨论稳定性,寻求满足不等式(21)的K,这就要计算Qn+1的模,而这是很困难的.设ρ(Q)为矩阵Q的谱半径,因为ρ(Q)≤‖Q‖恒成立,于是得到下面的结果. 定理1[22]差分格式(22)稳定的必要条件是 ρ(Q)≤1+CΔt, 其中,C是某一与Δt无关的非负常数. (3) 能量方法 考虑热传导问题 对方程(23)两边乘以u关于x积分,得: (26) 从而 (27) (28) 方程(23)的显示格式是 (30) 当n→∞时保持有界. 也即满足 在边界上满足条件 (33) 及 先将式(34)右端改写成 (37) 化简可得: 若定义 则 将式(38)代入式(41)中,得 因此En是n的单调下降函数.下面证明当n→∞时,‖zn‖2有界.对不等式 从j=0,1,…,M-1求和,得: 由En的定义,结合上式,得: En≥(1-2r)‖zn‖2, 又已证得En是n的单调下降函数,故 En≤En-1≤…≤E0≤‖z0‖2, 所以 由于‖z‖2称为能量,因此这种方法称为能量方法,能量方法原则上可用于变系数非线性方程. 定义2[23]空间L2(Ω)上面内积与范数分别定义如下: 定义3[23]空间L2(Ω)上面离散范数定义如下: 定义4[24](Taylor)如果f(x)的n+1阶导数连续,且fn+1(x)有界,那么 定理2[24]Schwarz不等式 |(u,v)|≤‖u‖·‖v‖, 引理1[25](离散Sobloev不等式)存在常数C1和C2有: ω(k)≤ρ(k)eCτk,∀k, 引理3[24](分部求和公式)对任意两个离散函数uh={uj|j=0,1,2,…,J}和vh={vj|j=0,1,2,…,J},有 文中记号如下: ‖un‖2=(un,un),un的2范数; 故对问题(1)~(3)考虑如下有限差分格式: 格式1 三层非线性差分格式 其中系数θ∈[0,1],还需要另一个二层的差分格式去计算u1. 格式2 二层格式 其中 又 将式(53)、式(54)代入式(52)中,然后得: (55) 将式(58)~式(60)代入式(57)得到: 定理4 式(45)~式(47)是唯一可解的. 证明 很显然u0被式(46)唯一确定,根据格式2,可知u1被u0确定.现可以猜想u0,u1,…,un是唯一可解的.考虑un+1. 取式(62)与un+1作内积,可得: (63) 根据差分性质和边界条件有 由式(63)、式(64)可得: (65) 即只有零解,因此式(45)~式(47)中un+1是唯一可解的. ‖u‖L2≤C,‖ux‖L2≤C,‖u‖∞≤C. (66) 证明 由式(43)得到‖u‖L2≤C,‖ux‖L2≤C,再由引理1知‖u‖∞≤C. 证明 由式(56)及Schwarz不等式有 即 由引理5、定理5及Cauchy-Schwarz不等式有 将式(70)~式(73)代入式(69)可以得到 并令 则式(75)变为 Bn+1-Bn≤2τ‖rn‖2+Cτ(Bn+1+Bn), 整理得: (1-Cτ)(Bn+1-Bn)≤2τ‖rn‖2+2CτBn. 如果τ适当小,满足1-Cτ>0,则有 Bn+1-Bn≤Cτ‖rn‖2+CτBn. (75) 将式(75)从0到n-1求和得: (76) 记 并且B0≤(O(τ2+h2))2,于是有 从定理6,可得: Bn≤(O(τ2+h2))2, 即 再由引理1有 ‖en‖∞≤(O(τ2+h2). 定理7 在定理6的条件下,式(45)~式(47)得解,un以‖·‖∞稳定. 考虑广义正则长波方程,现计算如下数值算列 在式(5)中,固定 由于本文的格式是3层的差分格式,但是3层格式在计算的时候不是自启动的,一般是需要先用2层格式计算第1层的数值解,然后才可以计算剩余时间层的数值解.为此考虑p=2和p=4两种情况进行数值实验.为了便于比较,记本文的格式为格式1,把θ分别取0,0.25,0.5,0.75,1.表1给出了当p=2时τ=0.1,h=0.05下的平方误差;表2给出了当p=2时本文差分格式与其他数值解法的平方误差的比较;表3给出了p=4时τ=h=0.1下的平方误差;表4给出了当p=4时本文差分格式与其他数值解法的平方误差的比较.通过表2和表4可以看出本文的差分方法是有效的和可行的. 表1 当p=2时取τ=0.1,h=0.05时,θ取不同值的平方误差Table 1 The square error of θ when taking different values,p=2,τ=0.1,h=0.05 表2 当p=2时取τ=0.1,h=0.05,本文差分格式与其他数值解法的平方误差 表3 当p=4时取τ=h=0.1时,θ取不同值的平方误差Table 3 The square error of θ when taking different values, p=4,τ=h=0.1 表4 当p=4时取τ=h=0.1时,本文差分格式与其他数值解法的平方误差 本文针对广义正则长波方程的数值解法进行了较为深入的研究,并提出了两个差分格式,通过分析可以获得这两个有限差分格式都满足能量守恒性质,同时通过用离散泛函的方法验证了求解广义正则长波方程的有限差分格式的收敛性和稳定性.此差分格式相对于前人(up)x复杂的离散过程中,计算量小,数值实验结果验证了本文差分格式比前人在求解数值解的误差精度方面得到了优化.但是广义正则方程的研究仍存在不足,有待进一步深化,例如在数值解方法方面可以对现有方法进一步优化或者寻找新的求解方法,使数值解更精确及满足更多的物理特征. 参考文献: [ 1 ]MOMONIATE.Amodifiedequationapproachtoselectinganonstandardfinitedifferenceschemeappliedtotheregularizedlongwaveequation[J].AbstractandAppliedAnalysis, 2014(2):1-14. [ 2 ]HUJ,XUY,HUB.Alineardifferenceschemefordissipativesymmetricregularizedlongwaveequationswithdampingterm[J].BoundaryValueProblems, 2011(1):1-16. [ 3 ]BHARDWAID.Acomputationalmethodforregularizedlongwaveequation[J].Computers&MathematicswithApplications, 2000,40(12):1397-1404. [ 4 ]IRKD.Solitarywavesolutionsfortheregularizedlong-waveequation[J].PhysicsofWavePhenomena, 2012,20(3):174-183. [ 5 ]LINB.ANonpolynomialsplineschemeforthegeneralizedregularizedlongwaveequation[J].StudiesinAppliedMathematics, 2014,132(2):160-182. [ 6 ]GUOPF,ZHANGLW,LIEWKM.Numericalanalysisofgeneralizedregularizedlongwaveequationusingtheelement-freekp-Ritzmethod[J].AppliedMathematicsandComputation, 2014,240(240):91-101. [ 7 ]MOHAMMADIR.ExponentialB-splinecollocationmethodfornumericalsolutionofthegeneralizedregularizedlongwaveequation[J].ChinesePhysicsB, 2015,24(5):177-190. [ 8 ]CHENL.Stabilityandinstabilityofsolitarywavesforgeneralizedsymmetricregularized-long-waveequations[J].PhysicaD:NonlinearPhenomena, 1998,118(1/2):53-68. [ 9 ]BONAJL,MCKINNEYWR,RESTREPOJM.Stableandunstablesolitary-wavesolutionsofthegeneralizedregularizedlong-waveequation[J].JournalofNonlinearScience, 2000,10(6):603-638. [10]DOGANA.NumericalsolutionofRLWequationusinglinearfiniteelementswithinGalerkin’smethod[J].AppliedMathematicalModelling, 2002,26(7):771-783. [11]TIANB,GAOYT.Symboliccomputationandobservableeffectforthe(2+1)-dimensionalsymmetricregularized-long-waveequationfromstronglymagnetizedcold-electronplasmas[J].Computers&MathematicswithApplications, 2003,45(4):731-735. [12]KAYAD.Anumericalsimulationofsolitary-wavesolutionsofthegeneralizedregularizedlong-waveequation[J].AppliedMathematics&Computation, 2004,149(3):833-841. [13]SOLIMANAA.NumericalsimulationofthegeneralizedregularizedlongwaveequationbyHe’svariationaliterationmethod[J].MathematicsandComputersinSimulation, 2005,70(2):119-124. [14]CAIJ.Anewexplicitmultisymplecticschemefortheregularizedlong-waveequation[J].JournalofMathematicalPhysics, 2009,50(1):321-377. [15]MOHAMMADIM,MOKHTARIR.Solvingthegeneralizedregularizedlongwaveequationonthebasisofareproducingkernelspace[J].JournalofComputational&AppliedMathematics, 2011,235(14):4003-4014. [16] 徐友才,胡劲松,胡朝浪. 广义正则长波方程的一个新的守恒差分格式[J]. 四川大学学报(自然科学版), 2011,48(3):534-538. XUYC,HUJS,HUCL.Anewconservationfinitedifferenceschemeforgeneralizedregularizedlongwaveequation[J].JournalofSichuanUniversity(NaturalScienceEdition), 2011,48(3):534-538. [17] 胡劲松,王玉兰. 广义正则长波方程的拟紧致守恒差分格式[J]. 东北师大学报(自然科学版), 2011,43(3):39-43. HUJS,WANGYL.Pseudo-compactconservationdifferenceschemeforgeneralizedregularizedlongwaveequation[J].JournalofNortheastNormalUniversity(NaturalScienceEdition), 2011,43(3):39-43. [18] 马亮亮. 变系数空间分数阶对流-扩散方程的有限差分解法[J]. 沈阳大学学报(自然科学版), 2013,25(4):341-344. MALL.Finitedifferencemethodforsolvingfractionalconvection-diffusionequationswithvariablecoefficients[J].JournalofShenyangUniversity(NaturalScience), 2013,25(4):341-344. [19] 魏义坤,杨威,刘静. 关于径向基函数插值方法及其应用[J]. 沈阳大学学报, 2008, 20(1):7-9. WEIYK,YANGW,LIUJ.Aboutradialbasisfunctioninterpolationmethodanditsapplication[J].JournalofShenyangUniversity, 2008,20(1):7-9. [20] 李荣华. 偏微分方程数值解法[M]. 北京:高等教育出版社, 2005:120-141. LIRH.Numericalsolutionofpartialdifferentialequations[M].Beijing:HigherEducationPress, 2005:120-141. [21] 孙志忠. 偏微分方程数值解法[M]. 北京:科学出版社, 2012:30-120. SUNZZ.Numericalsolutionofpartialdifferentialequations[M].Beijing:SciencePress, 2012:30-120. [22] 张文生. 科学计算中的偏微分方程有限差分法[M]. 北京: 高等教育出版社, 2006:235-268. ZHANGWS.Finitedifferencemethodforfinitedifferenceequationsinscientificcomputing[M].Beijing:HigherEducationPress, 2006:235-268. [23] 应隆安. 有限元方法讲义[M]. 北京: 北京大学出版社, 1988:30-113. YINGLA.Finiteelementmethodhandouts[M].Beijing:PekingUniversityPress, 1988:30-113. [24] 胡健伟,汤怀民. 微分方程数值方法[M]. 北京:科学出版社, 2011:169-200. HUJW,TANGHM.Differentialequationsnumericalmethods[M].Beijing:SciencePress, 2011:169-200. [25]SHAOX,XUEG,LIC.Aconservativeweightedfinitedifferenceschemeforregularizedlongwaveequation[J].AppliedMathematics&Computation, 2013,219(17):9202-9209. [26] 李荣华,冯果忱. 微分方程数值解法[M]. 北京: 高等教育出版社, 1996:24-60. LIRH,FENGGC.Differentialequationsnumericalmethods[M].Beijing:HigherEducationPress, 1996:24-60.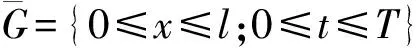
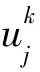
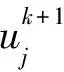
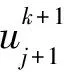
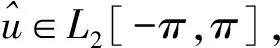
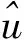
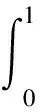


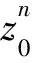
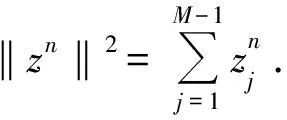
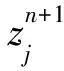
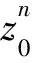
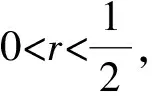
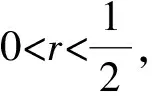
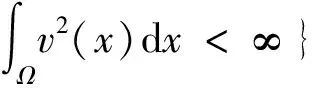
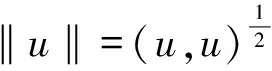
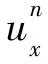
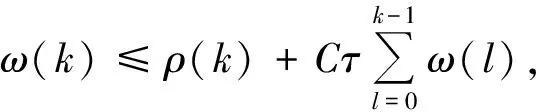


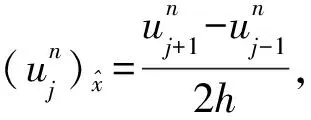
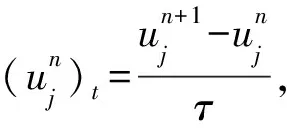
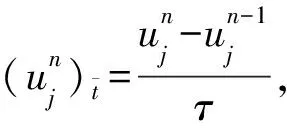
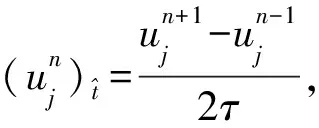
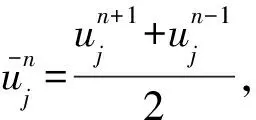
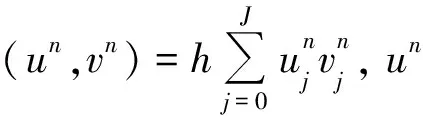
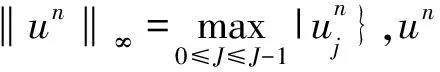
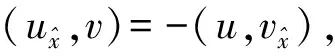

2 差分格式的建立
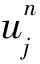
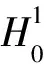
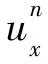
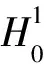
3 差分格式的可解性分析
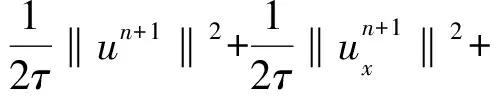
4 差分格式的误差分析
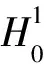
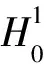

5 差分格式的收敛性与稳定性分析
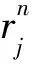
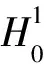
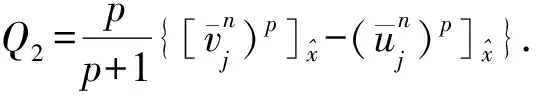

6 数值实验
7 结 论

