低碳视角下混合多属性决策的物流园区选址方法

李佳洋, 王 丹, 刘 洲, 戴 祥

(沈阳大学 信息工程学院, 辽宁 沈阳 110044)

随着国家低碳经济产业建设试点的推进,作为国家经济发展基础的物流业也必须找寻一条低碳运营和可持续发展的新模式.构建低碳物流园区是低碳物流系统的首要任务,而构建物流园区的第一步即为以低碳视角解决物流园区选址问题.尽管目前学术界尚未对低碳物流园区有标准化的界定,但是通过大量文献以及对目前已建物流园区的实践调研,可知低碳物流园区应具有产业聚集化、物流基础设施集中化、园区内外部资源共享化、信息平台协同化等特征.“低能耗、高效能”成为低碳物流园区的规划和建设的基本原则.由此,低碳物流园区的选址必须依据该原则展开.低碳物流园区的选址直接涉及到建成的物流园区对地方资源利用情况、物流运输线路低碳属性、是否符合节能减排要求等因素.因此,低碳物流园区的选址问题是一个多属性决策问题.本文尝试构建一种新型混合多属性决策方法,力求使低碳视角下物流园区的选址更符合低碳经济、循环经济以及物流产业园区的协同发展要求.

国内学者将低碳经济与物流相结合始于2008年,由戴定一首次提出,低碳物流有3个层面:技术层面为物流行业应采用节能减排创新技术;规划层面包括产业布局和物流系统解决方案的低碳化;同时,应以国家政策和制度建立保障低碳物流业向前发展.戴勇在此基础上提出了基于市场、政府、网络多样化治理机制和基于技术创新主导的3阶段演化的低碳物流园区运营优化策略.张立国在现有研究基础上,尝试着给出低碳物流园区的界定、特征和运行策略[1].张诚针对我国物流行业2010—2020年节能减排情况构建灰色预测模型进行预测,研究表明在“十三五”期间物流行业可以实现节能减排目标,并进一步优化物流行业能源结构[2].赵松岭通过对比美国、日本、欧洲等发达国家低碳物流的发展及特点,提出我国低碳物流发展中存在着宏观低碳发展政策缺失、物流行业碳排放指标不规范、运输环节能耗过高、配送系统不重视节能,以及低碳物流技术落后等困境[3].目前,国内学者对于低碳物流的理论研究主要集中于低碳物流的运营策略,以及低碳物流系统优化等方面,更侧重于宏观策略性研究,而对中观及微观低碳物流园区构建及设计细节研究不多.

低碳经济下物流选址问题的研究主要有严南南针对报废汽逆向物流网络的选址问题提出基于多级物流网络,构造物流总成本最小和碳排放量最小的双目标的数学规划模型[4].潘茜茜将碳排放因素加入冷链物流配送中心选址问题中,构建了运输成本、货损成本和碳排放处理成本最小化的多目标数学规划模型.王爽综合考虑城市物流中心选址问题的经济因素和环境因素,构建数学规划模型,并对比了考虑碳排放和不考虑碳排放的选址差异[5]. 刘涛研究了闭环物流网络选址模型,其以收益最大化为目标,整合了产品逆向物流、零部件逆向物流和废弃物逆向物流,并通过算例验证了模型的有效性[6].这些研究都是基于数学规划问题,而其中数据值都以精确数为基础.赵中杭根据对物流园区选址受到外界环境影响因素的不同,通过引入区间数来表示两两因素之间比较相对重要程度中的不确定性,并结合实例按步骤将区间层次分析法应用于物流园区的选址,是一种实用的物流园区选址决策的解决方案[7]. 胡郭军等人使用混合整数规划对农产品物流园区选址问题进行了研究[8].陈小兰在传统灰色关联分析法的基础上,对分辨系数和指标权重的确定进行了改进,建立了改进后的灰色关联评价模型,最后结合实际案例验证了该评价体系和评价模型的可行性和实用性[9]. 然而,低碳视角下物流园区选址问题涉及的内容极为广泛和复杂,既有定量化数据,也有定性化数据,因此,本文从这个角度提出基于混合多属性决策的低碳物流园区选址模型.

1 构建混合多属性决策的低碳物流园区选址方法

低碳视角下物流园区选址问题是多属性决策问题,而理想点法(TOPSIS)是解决多属性决策问题的典型方法.TOPSIS方法的基本思想是最佳选择方案应该是距离最佳理想点最近的方案,也是距离最差理想点最远的那个方案.在典型TOPSIS方法中,多属性指标的评价值和权重值是确定的.但是现实情况下,每一个属性指标的评价值未必都是精确数值,有些定性指标值是使用自然语言的,再或者一些数值型指标值是一个区间数.本文讨论的低碳视角下的物流园区选址问题属于混合多属性决策,决策值类型既包含精确值的定量化数值,也有定性数值,本文采用模糊集理论的三角模糊数表示定性数值.为了使其可求解,将这两类数值均转化为正负理想点法中的区间数,并进行决策.因此,本文将模糊集理论与TOPSIS结合,构造一种新的解决多准则决策问题的模糊区间数理想点法.在模糊TOPSIS方法中,指标的值和权重可以是精确值、区间数或模糊数.

1.1 区间数TOPSIS方法

第1步 构建模糊决策矩阵

假设有m个候选方案Ai(i=1,2,…,m),n个评价指标Cj(j=1,2,…,n),每个候选方案的指标值表示为区间数,建立区间数决策矩阵Xm×n,如表1所示.

表1 区间数决策矩阵Table 1 Interval number decision matrix

指标权重向量W=(w1,w2,…,wn),且满足指标权重公式

(1)

第2步 计算标准化决策矩阵

将决策矩阵Xm×n进行归一化处理得到标准化决策矩阵Hm×n,即将所有区间数转换成[0,1]之间的数值,转化公式如下:

第3步 构造加权标准化决策矩阵

加权决策矩阵表示为U,根据下面公式计算而得

(4)

第4步 计算决策矩阵正负理想点

根据带权标准化区间数决策矩阵,正负理想点的计算为:

其中F+j是Cj指标的正理想点,F-j是Cj指标的负理想点.

第5步 计算每个决策值和正负理想点的偏差

第6步 计算相关系数,并按照相关系数排序

计算每个候选方案的相关系数ξi,公式为

(9)

候选方案的相关系数越接近1,说明其评价值越接近正理想点,远离负理想点.对每个候选方案的ξi进行降序排序,其值最高的为最优选择方案.

1.2 相关系数及标准差整合法确定指标权重

此前的TOPSIS方法中权重通常采用层次分析法(AHP)结合专家评价法而得.本文引入Wang在2010提出使用相关系数及标准差整合法的基本原理确定多准则决策中的指标权重[10].在确定各指标权重时考虑该指标与其他指标的标准差以及它和所有被选方案的相关系数.该相关系数决定方法为:将该指标从指标集中移出,计算决策值;如果新的决策值与含有全部指标的决策值比较没有任何变化,那么说明该指标不重要,既被赋予较低权重;否则该指标被赋予较高权重.最终相关系数及标准差整合法的方法中的指标权重值需要建立非线性优化模型求得.

为了求得相关系数,设置变量λi为加权决策矩阵各值的线性加和:

(10)

然后,将指标Cj从指标集中移出,重新计算决策估值:

(11)

相关系数ρj计算公式为

(12)

其中:

如果ρj接近1,说明移出Cj对决策结果没有任何影响,所以可以给它赋予较小权重.如果ρj很小,接近-1,说明移出Cj对决策结果有很大影响,是决策必不可少的内容,所以必须赋以较大权重.基于以上,各指标权重应该由公式(15)计算而得

(15)

其中,σj是Cj指标的标准差,见公式(16):

(16)

1.3 数据转换

在混合多属性决策中,决策值可能以自然语言描述,也可能是精确的数值、模糊数值等形式,必须将其转化成区间数.

自然语言值通常直接使用传统数值型无法很好描述,可以考虑自然语言值划分等级.本文定义了自然语言描述等级包括:非常好(VG),很好(MG),好(G),一般(F),差(P),很差(MP),非常差(VP).这些等级可以转换成三角模糊数,他们之间关联关系如表2所示.

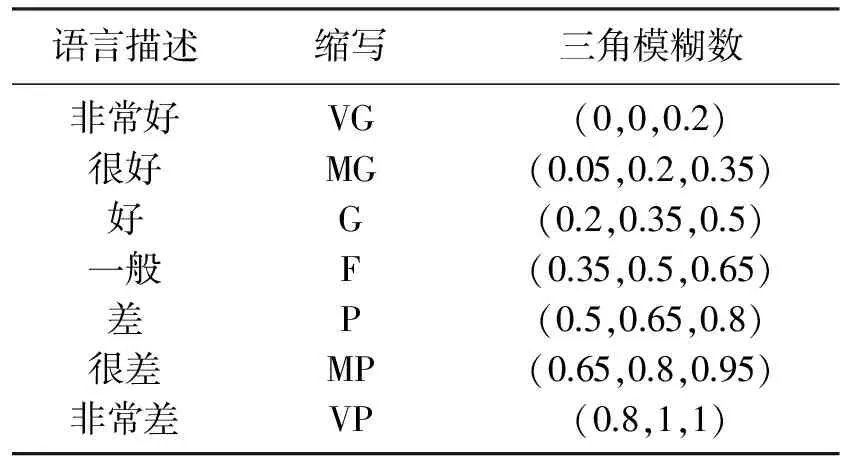
表2 模糊语言和相对应的模糊数

(17)

其中,0≤α≤1.

1.4 混合多属性决策的物流园区选址模型的基本操作

混合多属性决策的物流园区选址模型的基本操作见图1.

图1混合多属性决策的物流园区选址模型的基本操作

Fig.1 The operation flow of the location model of logistics park with mixed multi-attribute decision-making

2 算例分析

为了验证本文构造的算法的有效性和可操作性, 本文依据参考文献[11-12]中的背景数据并对其物流园区选址的指标体系进行改造. 低碳视角下物流园区选址必须加入环境因素, 本文从物流园区所在区域的经济因素、社会因素、内在因素制定低碳物流园区选址决策的指标体系如表3所示.

表3 低碳物流园区选址决策指标体系

本文中选取案例为关中-天水经济区,规划范围包括陕西西安、咸阳、铜川、渭南、宝鸡、商洛、杨凌农业高新技术产业示范区和甘肃天水所辖行政区域.直接辐射区域包括陕西省陕南的汉中、安康,陕北的延安、榆林,甘肃省的平凉、庆阳和陇南地区.经济区地处亚欧大陆桥中心,处于承东启西、联接南北的战略要地.目前,经济区内的软硬环境都得到了极大的改善,已经拥有国家级和省级开发区21个,高新技术产业孵化基地5个和大学科技园3个等.

在低碳经济倡导下,关中-天水经济区拟在8个子区域选建物流园区.针对各候选方案的各项指标值,构建初始选址决策矩阵;如表4所示.

初始决策矩阵运用式(2)、式(3)、式(17)、式(18)转换为区间数决策矩阵,并使用式(1)及式(10)～式(16)确定各指标权重值,加权区间数决策矩阵及权重值,如表5所示.

表4 初始决策矩阵Table 4 Initial decision matrix

表5 加权标准化区间数决策矩阵及各指标权重Table 5 Weighted standard interval number decision matrix and index weight

运用式(4)～式(9)计算每个候选方案正负理想点,以及评价值对理想点的偏差的相关系数,按照相关系数排列为

ξ4>ξ2>ξ1>ξ5>ξ6>ξ8>ξ7>ξ3.

结果表明,在关中-天水经济区规划物流园区选址时,充分考虑低碳因素可以选择渭南、咸阳、西安作为物流园区规划,避开铜川和杨凌.此结论基本与参考文献[8]的结论一致,并比该文献更加细化每个候选地的优先选择系数,对于低碳物流园区的选址问题更具有可操作性和科学依据.

4 结 论

本文构建一个基于混合多属性的区间TOPSIS决策方法,用于低碳视角下物流园区选址决策的研究.首先通过分析低碳物流园区选址问题的相关因素,构建了一套综合考虑内部因素、外部因素、经济因素、环境因素的指标体系.该指标体系去繁存简,更易于运用科学决策分析模型.本文构造的低碳物流园区选址方法,既考虑定性问题又考虑定量问题,对于决策中一些不确定的指标值,应用模糊逻辑或者区间数表示,采用相关系数和标准差的方法确定指标权重,尽可能减少主观因素.最后通过实例证明了该方法在低碳物流园区选址决策的问题上具有较好的效果.

参考文献:

[ 1 ] 范立南,董冬艳,李佳洋,等. 基于生鲜农产品的冷链物流配送路径优化[J]. 沈阳大学学报(自然科学版), 2017,29(2):125-131.

FANLN,DONGDY,LIJY.Routeoptimizationofcoldchainlogisticsbasedonfreshagriculturalproducts[J].JournalofShenyangUniversity(NaturalScience), 2017,29(2):125-131.

[ 2 ] 张诚,周安,张志坚. 基于灰色预测模型的物流低碳效应分析[J]. 统计与决策, 2014(16):89-91.

ZHANGC,ZHOUA,ZHANGZJ.Lowcarboneffectanalysisbasedongreypredictionmodel[J].Statistics&Decision, 2014(16):89-91.

[ 3 ] 赵松岭. 国内外低碳物流发展的比较与借鉴[J]. 对外经贸实务, 2014(1):90-92.

ZHAOSL.Domesticandforeignlow-carbonlogisticsdevelopmentcomparisonandreference[J].EconomicRelationsandTrade, 2014(1):90-92.

[ 4 ] 严南南,李明. 基于低碳的报废汽车逆向物流网络选址问题研究[J]. 重庆交通大学学报(自然科学版), 2016,35(5):180-184.

YANNN,LIM.Locationselectionforlogisticsnetworkforrecycledscrapedmotorcarbasedonlow-carbonprinciple[J].JournalofChongqngJiaotongUniversity(NaturalScience), 2016,35(5):180-184.

[ 5 ] 潘茜茜,干宏程,刘勇. 低碳经济下冷链物流配送中心选址设计[J]. 物流科技, 2015,38(9):29-31,35.

PANXX,GANHC,LIUY.Thedesignofdistributioncenterlocationaboutthecoldsupplychainbasingonthelow-carboneconomy[J].LogisticsSci-Tech, 2015,38(9):29-31,35.

[ 6 ] 刘涛. 低碳经济下的闭环物流网络选址问题研究[J]. 物流科技, 2015,38(12):84-88.

LIUT.Researchonthelocationproblemofclosed-looplogisticsnetworkbasedonlowcarboneconomy[J].LogisticsSci-Tech, 2015,38(12):84-88.

[ 7 ] 赵中杭. 区间层次分析法在物流园区选址中的应用[J]. 现代商贸工业, 2017(17):35-36.

ZHAOZH.Theapplicationofintervalanalytichierarchyprocessinsiteselectionoflogisticspark.[J].ModernBusinessTradeIndustry, 2017(17):35-36.

[ 8 ] 胡郭军,张从翔,高德宝. 混合整数模型在农产品物流园区选址中的应用[J]. 中外企业家, 2015(28):63-66.

HUGJ,ZHANGCX,GAODB.Applicationofmixedintegermodelinsiteselectionofagriculturallogisticspark[J].ChineseandForeignEntrepreneurs, 2015(28):63-66.

[ 9 ] 陈小兰,邹欣. 改进灰色关联分析法在物流园区选址合理性评价中的应用[J]. 物流工程与管理, 2015,37(9):110-113.

CHENXL,ZOUX.Applicationofimprovedgreyrelationalanalysismethodinrationalityevaluationoflogisticsparklocation[J].LogisticsEngineeringAndManagement, 2015,37(9):110-113.

[10]WANGTC,LEEHD.DevelopingafuzzyTOPSISapproachbasedonsubjectiveweightsandobjectiveweights[J].ExpertSystemswithApplications, 2009,36(5):8980-8985.

[11] 周勇,马元洁. 产业集聚视角下物流园区的选址问题[J]. 物流科技, 2015,34(22):144-148.

ZHOUY,MAYJ.Studyonlogisticsparklocationproblem:anindustrialconglomerationperspective[J].LogisticsSci-Tech, 2015,34(22):144-148.

[12] 文武,王小侠. 企业内部物流的标准化管理与信息化应用[J]. 沈阳大学学报(社会科学版), 2012,14(5):11-13.

WENW,WANGXX.Standardizedmanagementandinformationtechnologyapplicationsofinternallogisticsinenterprises[J].JournalofShenyangUniversity(SocialScience), 2012,14(5):11-13.