二四混水平因子设计在Lee偏差下的均匀性*

胡柳平，刘佳琦，王 康，欧祖军

(吉首大学数学与统计学院，湖南 吉首 416000)

均匀设计[1]是一种重要的计算机试验，它要求试验点均匀分布在试验区域中，具有模型稳健的优点.一般采用偏差来衡量设计的均匀性.对于一个设计，若没有其他设计比它有更小的偏差，则称该设计为均匀设计.Lee偏差[2]作为一种均匀性测度，克服了可卷型L2-偏差[3-5]的局限性.周永道等[2]给出了Lee偏差与广义最小低阶混杂准则[6]之间的解析关系，并获得了Lee偏差值的一个下界.邹娜等[7]给出了二水平、三水平设计的Lee偏差与最小矩混杂准则[8]之间的解析关系，以及二水平、三水平设计的Lee偏差值的下界.对于二三混水平设计，K Chatterjee等[9]、张琼慧[10]讨论了Lee偏差与最小矩混杂准则、Lee偏差与正交性之间的关系，并给出了二三混水平设计的Lee偏差值的下界.事实上，二四混水平设计是应用最广泛的混水平因子设计，雷秩菊[11]给出了它在可卷型L2-偏差下的下界.笔者拟研究二四混水平因子设计在Lee偏差下的均匀性.

1 预备知识

(1)

2 主要结果及其证明

对于任意设计d(d∈U(n;2s14s2))，其中s1+s2=s，由(1)式可得其Lee偏差计算表达式为

(2)

其中：

当1≤k≤s1和s1+1≤k≤s时，分别有：

其中：Ω1={(0,1),(1,0),(1,2),(2,1),(2,3),(3,2),(0,3),(3,0)}；Ω2={(0,2),(2,0),(1,3),(3,1)}.定义如下符号：

(3)

其中|Ω|表示集合Ω的势.那么，由(2)，(3)式可得如下结论：

引理2对于任意设计d(d∈U(n;2s14s2)),有：

将(2)式改写成含有参数λij,ξij,ηij的形式，则有如下结论：

定理1对于任意设计d(d∈U(n;2s14s2))，有

证明由(2)，(3)式和引理2，有

当i,j(≠i)=1,…,n时，所有的δij都相等(记作θ),由引理2可知

(4)

此时,类似于文献[12]中定理2.1的证明，由定理1和(4)式可得如下结论：

特别地，对于任意设计d(d∈U(n;2s14s2))，当s1=0或s2=0时，由定理1和定理2可得如下结论：

推论1对于任意设计d*(d*∈U(n;2s)),d**(d**∈U(n;4s))，有

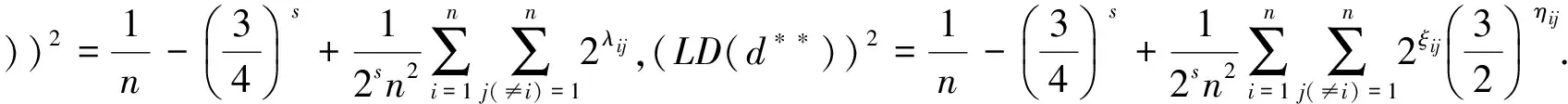
由推论1和引理1不难得出如下结论：

推论2对于任意设计d*(d*∈U(n;2s))，d**(d**∈U(n;4s))，有

(LD(d*))2≥LB(LD(d*)),(LD(d**))2≥LB(LD(d**)).

其中：

这里：

3 实例

为了方便起见，将定理2中的(LD(d))2记作LD,下界LB(LD(d))记作LB.为了比较设计的优劣，定义设计d的效率Eff(d)=LB/LD，若Eff(d)=1，则设计d为Lee偏差下的均匀设计.

例1考虑以下6个设计：d1∈U(4;2242),d2∈U(4;2441),d3∈U(4;2343),d4∈U(4;2641),d5∈U(4;2643),d6∈U(4;2943).其中：n=4；s1分别为2，4，3，6，6，9；s2分别为2，1，3，1，3，3.表1给出d1—d6的设计.

表1 设计d1—d6Table 1 Designs of d1 to d6

由表1的数据可计算出6个设计的Lee偏差平方值、下界和效率，如表2所示.

表2 d1—d6的Lee偏差平方值、下界和效率Table 2 Values of Squared Lee Discrepancy,Lower Bound and Efficiency for Designs of d1 to d6

从表2可知LB是可达的，即是一个紧的下界，这样的下界可以作为搜索Lee偏差下二四混水平均匀设计的一个基准.

参考文献：

[1] FANG Kaitai,WANG Yuan.Number-Theoretic Methods in Statistics[M].London:Chapman and Hall,1994：200-246.

[2] ZHOU Yongdao,NING Jianhui,SONG Xiebing.Lee Discrepancy and Its Applications in Experimental Designs[J].Statistics and Probability Letters,2008,78(13):1 933-1 942.

[3] HICKERNELL FRED J.A Generalized Discrepancy and Quadrature Error Bound[J].Mathematics of Computation,1998,67(221):299-322.

[4] CHATTERJEE K,FANG K T,QIN Hong.Uniformity in Factiorial Designs with Mixed Levels[J].Journal of Statistical Planning and Inference,2005,128(2):593-607.

[5] CHATTERJEE KASHINATH,LI Zhaohai,QIN Hong.Some New Lower Bounds to Centered and Wrap-RoundL2-Discrepancies[J].Statistics and Probability Letters,2012,82(7):1 367-1 373.

[6] XU Hongquan,WU C F J.Generalized Minimum Aberration for Asymmetrical Fractional Factorial Designs[J].The Annals of Statistics,2001,29(2):549-560.

[7] ZOU Na,REN Ping,QIN Hong.A Note on Lee Discrepancy[J].Statistics and Probability Letters,2009,79(4):496-500.

[8] XU Hongquan.Minimum Moment Aberration for Nonregular Designs and Supersaturated Designs[J].Statistica Sinca,2003,13(3):691-708.

[9] CHATTERJEE KASHINATH,QIN Hong,ZOU Na.Lee Discrepancy on Asymmetrical Factorials with Two-and Three-Levels[J].Science China Mathematics,2012,55(3):663-670.

[10] 张琼慧.二三混水平因子设计的Lee-偏差和可卷型L2-偏差的新下界[D].武汉:华中师范大学,2013:9-10.

[11] 雷秩菊.2和4混水平U-型设计在可卷L2-偏差下的下界[J].北京教育学院学报(自然科学版),2016,11(1):1-4.

[12] FANG Kaitai,TANG Yu,YIN Jianxing.Lower Bounds for Wrap-AroundL2-Discrepancy and Constructions of Symmetrical Uniform Designs[J].Journal of Complexity,2005,21(5):757-771.