基于鲁棒优化模型的农产品供销问题研究*
李丽丽,王 斌
(山西农业大学信息科学与工程学院,山西 太谷 030801)
0 引言
在将农产品运往市场之前,我们往往无法预测到市场的需求情况。当对需求地的供应量大于需求地的需求量时,这种供大于求的市场局面导致的结果将是农产品滞销,价格下跌,又由于农产品的保质期一般都比较短,从而对销售者而言势必造成一定的损失。但是另一方面,若对需求地的供应量小于需求地的需求量时,虽然能够短期内将农产品销售出去,但也会由于小的供应量使得销售者不能获得最大效益。因此,对销售者而言如何决定运往需求地的运量是亟待解决的问题。曲亚萍[1]为克服疏散交通管理中需求信息的不确定性,运用鲁棒优化的思想将原来的确定型模型转化为不同不确定需求情况下的鲁棒对应模型;刘希慧[2]针对农业资源运输中以及农产品的收购和集中销售点问题的鲁棒性问题为研究背景,根据农业资源中的运输条件的各种影响因素建立混合鲁棒优化模型。
在将农产品运往市场之前,我们往往无法预测到市场的需求情况。而且历史数据通常极其有限无法明确其准确的概率分布。因此,采用一种优化方法,纳入需求信息缺失的特征且无需考虑需求的具体分布。基于此,提出了一种不确定环境下的建模策略[3,5-9]。它将鲁棒思想用于随机优化的模型中[4],在只知道概率分布所满足的一些条件下,比如一阶矩信息、二阶矩信息以及支撑集合信息等,寻求所有满足条件的分布中使目标函数最差的可能分布,并在最差的分布下找寻最优解的一种方法。
1 问题描述及农产品运输的鲁棒模型
1) 假设农产品的保质期都非常短且不易贮存;
2) 考虑一种类型的农产品运往多个销售地;
3) 假设运输途中没有农产品的损耗。
相关符号为:
1.1 参数
n:销售地的个数;
c=(c1,c2,…,cn):ci运往销售地i单位农产品的成本;
Mi:运往销售地i农产品的成本预算;
λi:运输量超过销售地i市场的需求量时单位农产品的持有成本;
h1:对销售者而言,运量满足销售地需求的单位收益效用系数;
h2:对销售者而言,运量未满足需求的单位损失效用系数;
wk:由于市场的变化及环境等外界因素变化的可能情况,k=1,2,...,v;
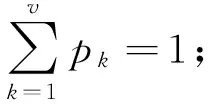
xi(wk):情景wk下销售地i农产品的需求量。
1.2 决策变量
r=(r1,r2,…,rn):对各销售地农产品的运量,其中ri表示运往销售地i农产品的运量。
我们用一个分段线性函数来刻画需求地农产品资源需求的效用函数[1]:
在农产品供应中,若农产品资源供应量大于需求量可能对销售者造成无法补救的损失,而且根据Tversky& Kahneman的前景理论,本文认为h1 销售者对销地所需农产品的需求量很难做出准确的估计,但根据以往的经验,资源需求量x为满足如下条件的概率分布: Γ(μ,σ2)={F∶EF[x]=μ,EF[x2]=μ2+σ2}.(2) 其中,μ为需求分布的均值,μ2+σ2为需求分布的方差。销售者要基于以上的有限信息进行决策,为了克服由于需求分布信息缺失所造成的困难,我们以最小化最差分布下的总成本为目标,构建鲁棒资源配置模型。 (3) 模型等价于 (4) maxf(ri)=maxF∈Γ(μ,δ2)EF[U(ri,xi(wk))]-ciri (5) 等价于下面的形式 min-f(ri)=maxF∈Γ(μ,δ2)EF[Q(ri,xi(wk))]+ciri (6) 首先,分析模型内部的极大化问题maxF∈Γ(μ,δ2)EF[Q(ri,xi(wk))],受Scarf(1958)[10]利用对偶方法求解模型的启发,我们将上述极大化问题视为原问题。 (7) 则它的对偶问题为 (8) 令1(xi(wk))=y1+xi(wk)y2+xi(wk)2y3,Q(r)=maxF∈Γ(μ,δ2)EF[Q(ri,xi(wk))],F*(xi(wk))为原问题的最优解,(y1,y2,y3)为对偶问题的最优解。若强对偶定理成立,则原问题与对偶问题的最优解满足互补松弛条件: (9) (10) 原问题的最优解dF*(xi(wk))拥有非零概率。换言之,原问题的最优解应在l(x)和Q(r,x)的公共点处取得,并且知道l(x)和Q(r,x)至多有2个公共点。 基于上述分析,我们在下面的定理中给出最差分布下应急决策者资源的最优储备量的闭式表达式。 定理[2]: (ii)若: (11) 运往销售地i的最优运输量为: (12) (iii)若: (13) 证明:令p1=p(x1),p2=p(x2),则问题化为: (14) 情形1:假设l(x),Q(r,x)相切,两个切点的横坐标为x1,x2,且0 l(x1)=Q(r,x1) (15) 根据等式组(12),易于求出x1+x2=2r;且x1,x2应满足可行性条件: (16) 同时对偶问题的可行解为 (17) Q1(r)=Q(r,x1)p1+Q(r,x2)p2= y1+μy2+(μ2+σ2)y3= (h1+h2+λ)+rλ+h2μ. (18) 因此原问题与对偶问题的强对偶性成立。 情形2:假设l(x),Q(r,x)相切与一点,相交于一点,设交点的横坐标为x1=0,即(0,rλ),切点的横坐标为x2。有下面的等式成立 (19) 根据上面等式求出对偶问题的最优解 (20) x1,x2应满足原问题的约束条件,从而求得 (21) 综上,两点分布F(x):(xi,pi),i=1,2是满足互补松弛条件的原问题的可行解,(y1,y2,y3)是满足互补松弛条件的对偶问题的可行解。同样,容易验证原问题和对偶问题的最优目标值等同: (22) 因此,原问题与对偶问题的强对偶性质成立。 综上两种情形,最差分布下第二阶段的成本与效用损失之和最大为: (23) (24) 下面,我们证明f(r)=Q(r)-cr在区间[0,+∞)上的可微性。 因为Q(r)是由两种分布情形下的函数分段组合而成,而这两个函数显然都是可微的,所以我们只需要证明在两种情形的连接点处也是连续可微的。 (25) 其一阶导数 (26) 进而,其二阶导数为: (27) (28) 由于市场对农产品的需求量往往受外界环境的影响,我们对农产品的需求量很难做到准确的把握,如果农产品销售者盲目的决定运往需求地的运量将会使其造成一定的损失,从而得不到最大利润。本文通过建立鲁棒优化模型得到了在不同市场情况下运往销售地的最佳运量,从而对农产品销售者而言可以获得最大利润。这将对农产品的经营者如何经营提供了理论基础。 [1] 曲亚萍.突发事件下应急资源管理的鲁棒决策研究[D].重庆:重庆大学,2014. [2] 刘希慧.基于鲁棒优化模型的农业资源配置研究[D].舟山:浙江海洋学院,2014. [3] 黄为.基于鲁棒优化的应急资源配置研究[D].西安:西安电子科技大学,2012. [4] 徐家旺,黄小原.鲁棒优化研究的新进展[J].中国企业运筹学,2007(1):14-20. [5] 朱丽,李春发.成本控制下考虑多商品物流配送线路安排的鲁棒优化模型[J],天津理工大学学报,2012(3):76-79. [6] 张玲,王晶,黄钧.不确定需求下应急资源配置的鲁棒优化方法[J].系统科学与数学,2010,30(10):1283-1292. [7] 张玲,董银红,张敏.基于情景分析的应急资源布局决策[J].系统工程,2014(3):137-142. [8] 寿涌毅,姚伟建.信息不确定下项目组合选择问题的鲁棒优化[J].系统工程,2009(7):90-95. [9] 陈新林,张双武.多供应商竞争下再制造闭环供应链鲁棒生产计划[J].系统工程,2010(4):41-47. [10] Scarf H. A min-max Solution of an Inventory Problem [J]. In: Arrow K, Karlin S, Scarf H (eds),Studies in the Mathematical Theory of Inventory and Production.California: Stanford University Press,1958:201-209.2 需求信息缺失下的鲁棒资源配置模型
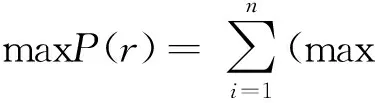
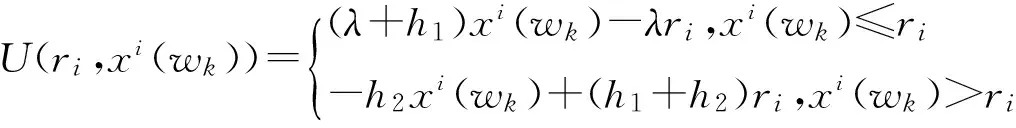
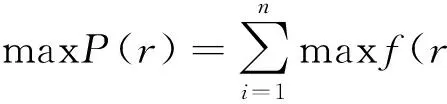
3 模型求解
s.t.ciri≤Mi
ri≥0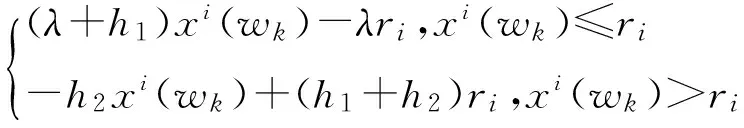
s.t.ciri≤Mi
ri≥0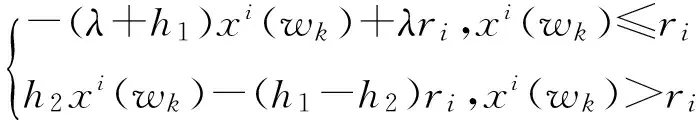

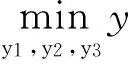
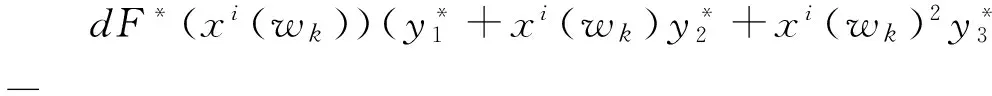
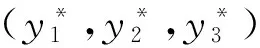
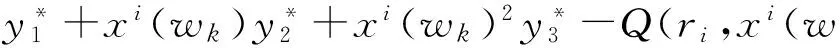
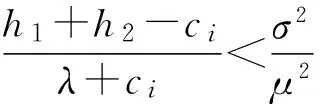
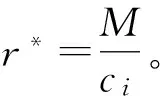
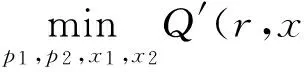
l′(x1)=Q′(r,x1)
l(x2)=Q(r,x2)
l′(x2)=Q(r,x2)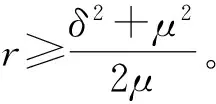
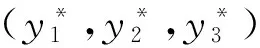
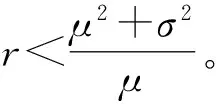
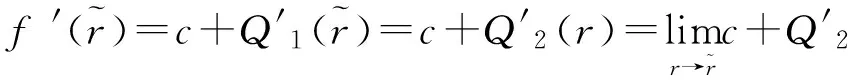
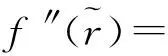
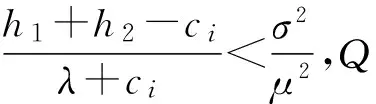
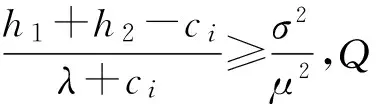
5 结束语
——《民法典》删除《侵权责任法》第42条之解读

