基于粒子群算法的植保无人机航线规划*

武锦龙

(山西农业大学 信息科学与工程学院，山西 太谷 030801)

随着国内精准农业、食品安全等领域的不断发展，农用航空领域发展极其迅速，无人机已经广泛应用至农田的遥感监测、施肥施药等领域[1]。植保无人机具有飞行高度低，尺寸小、可悬停、受周围环境限制影响较少等优点，在实际农业应用领域有较大的发展前景。但是，目前已经投入使用的植保无人机，大部分仍然是依赖人工去遥控的，无人机操控技术相对较难，会偏移路线，造成药剂、化肥的重复喷洒和漏喷现象，实际工作效果并不理想。为了降低人工成本，减轻植保无人机操控人员的工作强度，同时使植保作业更加精准、节能，在作业前如何根据实际地形进行作业路径规划，已经是当前植保无人机实际作业时需要解决的一个重要难题。

目前，无人机的航迹研究大多规划出的是最优或满意的飞行航迹。唐必伟等[2]研究了基于蚁群算法的无人机二维航迹规划。方徐博等[3,4]等分别针对单个和多个不规则区域提出了单个作业区域的航线规划和多作业区域航线的全局规划。王宇等[5]提出基于Grid-GSA算法的植保无人机路径规划。张仁鹏等[6]研究了基于改进粒子群算法的在线航迹重规划。而针对植保无人机的路径规划问题，国内才处于起步阶段。本文针对多个规则作业区域情况，提出了一种基于粒子群算法的全局作业路径，不仅能够完成各区域内部的作业路径规划，而且能够实现区域间的最优航线规划，实现障碍物躲避，最终实现植保无人机的全局航线规划。

1 无人机航迹规划模型

1.1 规则区域作业方式选择

对于规则区域的传统地面作业方式，常用的方式为牛耕往复法和内外螺旋法。由于无人机的机械特性，在转弯的时候无法进行喷药作业，所以对于植保无人机的作业形式，本文根据文献[3]选择了转弯相对较少，喷药覆盖率相对较高的牛耕往复回转法，具体作业方式如图1所示，其中d为植保无人机的喷药工作半径，工作区域为L*H的规则矩形。

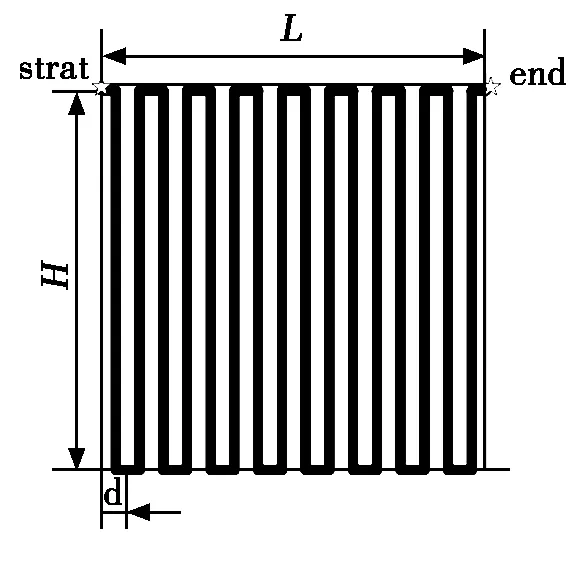
图1 牛耕往复法示意图

1.2 路径航迹适应度函数

在无人机航迹规划中，常用的简化的航迹代价计算公式为：

(1)

将航迹代价函数[9]可以作为粒子群算法的适应度函数，其中J为无人机航迹代价值，s为分析过程中将一个完整飞行航迹分成的段数，Li表示航迹中第i段的飞行长度，Hi为航迹中第i段的平均高度，Ti表示的是航迹中第i段的平均威胁指数。k1、k2、k3分别为长度、高度、威胁指数所占的权重。同时，粒子适应度函数中的飞行距离L、飞行高度H、威胁指数T需要满足无人机实际飞行过程中的约束条件，比如最大转弯角、最大爬升高度等等。

2 粒子群算法

PSO算法的工作原理如下：包含N个粒子的粒子群，在D维优化空间中不断修正自身位置信息寻找最优解。每个粒子都表示问题的一个解，第i个粒子的位置信息可以表示为Xi={xi1,xi2,…,xiD}，第i个粒子的速度信息为Vi={vi1,vi2,…,viD}。粒子不停修正自身位置信息能够找到经过的最优的位置，其中第i个粒子经过的最好位置可以表示为Pibest={pi1,pi2,…,piD}，为一个局部最优值，整个种群所经历的最好位置可以表示为Pgbest={pg1,pg2,…,pgD}，为全局最优值。通过如下公式进行更新：

(2)

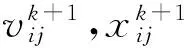
3 植保无人机路径规划

3.1 航迹空间下的粒子编码方式

植保无人机工作路径可解析为粒子群可以识别并优化的模型。其编码方式[12]如下：将出发点和目标点在x轴方向上进行n等分，然后在y轴方向上随机生成n-1个数值作为初始值，可作为一个粒子的粒子编码。所以，第i个粒子的初始坐标信息可通过如下公式得到：

xij=xstart+j·(xgoat-xstart)/(n-1)
yij=ystart+rand()·(ygoat-ystart)

(3)

其中，(xstart，ystart)，(xgoat，ygoat)分别为无人机飞行航迹的起始点和目标点，rand函数能够生成区间[0,1]上的随机数。通过该公式即可得到一系列的点坐标值：(xstart，ystart)、(xi1，yi1)、(xi2，yi2)…(xgoat，ygoat)。将坐标值进行连接，则是第i个粒子代表的初始路径，其起始点和目标点的位置始终不变，如图2所示。

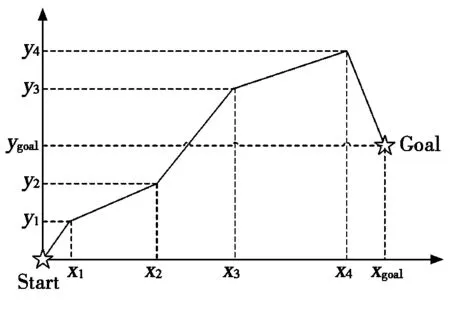
图2 粒子编码示意图

3.2 植保无人机路径规划步骤

植保无人机路径规划的步骤如下：

Step1:将需要进行植保作业的d块区域进行输入，采用牛耕往复法求解每个区域作业的开始点和截止点。

Step2:初始化粒子种群，初始化N个粒子的初始位置(xi1，yi1)和初始速度vij等相关参数。初始化路径需要经过每一区域的开始点和截止点，保证位置信息不变。

Step3:计算粒子的适应度值，将每个粒子的局部最优解pibest初始化为当前粒子，并初始化全局最优值pgbest=pibest。

Step4:根据式，更新粒子的位置与速度，令i=0,j=0。

Step5:j=j+1,如果j>n转到setp6，否则，转到setp4。

Step6:i=i+1,如果i>N，转到setp7，否则，转到setp4。

Setp7:当粒子适应度函数值大于局部最优值时，更新局部最优值，同理当局部最优值大于全局最优值时，更新全局最优值。

Setp8:判断是否满足迭代结束条件,满足则转到setp9，否则继续进行迭代。

Setp9:迭代结束，全局最优值pgbest中的所含的路径即为最优路径，结合牛耕往复法，即可得到全局最优路径。

4 仿真分析

仿真实验场景设置在1200m*700m的工作区域，区域内部分布着三个规则作业区域(农田)，五个障碍物。农田具体分布情况如表1所示。航迹过程中的障碍物可以简化建模为圆形障碍物，其具体分布情况如表2所示。

表1 农田(矩形)分布情况

表2 障碍物(圆形)分布情况

针对仿真实验场景，进行全局植保无人机航线规划，全局航迹应完成喷洒任务和障碍物躲避，到达目标农田。实验过程中，粒子群算法的参数设置为，粒子群数量：30；最大迭代次数：200；学习因子：c1、c2均为1.5，航迹规划结果如图3所示。航迹适应度函数的收敛曲线如图4所示，发现该航迹规划在迭代30次左右就收敛于最优航迹。

图3 航迹规划结果

图4 粒子群算法收敛曲线图

5 结论

本文提出的基于粒子群算法的植保无人机路径规划，基于植保无人机的实际需求，将多块区域作业路径问题转化为粒子群算法的优化模型。路径规划是非常繁杂的优化问题，理论上不存在绝对的最优解，只能得到向最优解逼近的近似最优解。相对于原来的手工作业，提高了路径的精确性和稳定性。本文提出的粒子群算法的植保无人机路径规划算法，较好找到植保无人机在实际植保作业的近似最优路径。

[1] 张东彦,兰玉彬,陈立平,等.中国农业航空施药技术研究进展与展望[J].农业机械学报,2014,45(10):53-59.

[2] 唐必伟,方群,朱战霞,等.基于改进蚁群算法的无人飞行器二维航迹规划[J].西北工业大学学报,2013,31(5):683-688.

[3] 徐博,陈立平,谭彧,等.基于无人机航向的不规则区域作业航线规划算法与验证[J].农业工程学报,2015(23):173-178.

[4] 徐博,陈立平,徐旻,等.多作业区域植保无人机航线规划算法[J].农业机械学报,2017,48(2):75-81.

[5] 王宇,陈海涛,李煜,等.基于Grid-GSA算法的植保无人机路径规划方法[J].农业机械学报,2017,48(7):29-37.

[6] 张仁鹏,杨金孝,潘佳华,等.基于改进粒子群算法的无人机三维航迹规划[J].计算机仿真,2014,31(3):65-69.

[7] 徐博,陈立平,谭彧,等.多架次作业植保无人机最小能耗航迹规划算法研究[J].农业机械学报,2015,46(11):36-42.

[8] 张仁鹏,杨金孝,潘佳华,等.基于改进粒子群算法的无人机三维航迹规划[J].计算机仿真,2014,31(3):65-69.

[9] 方群,徐青.基于改进粒子群算法的无人机三维航迹规划[J].西北工业大学学报,2017,35(1):66-73.

[10] 黄太安,生佳根,徐红洋,等.一种改进的简化粒子群算法[J].计算机仿真,2013,30(2):327-330.

[11] 胡旺,李志蜀.一种更简化而高效的粒子群优化算法[J].软件学报,2007,18(4):861-868.

[12] 张建南,刘以安,王刚.基于优化粒子群算法的无人机航路规划[J].传感器与微系统,2017,36(3):58-61.