一种基于二分法的快速目标点迹模拟方法

丁 春，姚 远，王 奇

(中国船舶重工集团公司第七二四研究所，南京 211153)

0 引 言

在雷达研制过程中，为了提高目标跟踪的可靠性，验证自动起始和目标跟踪算法是不可或缺的环节。一般是通过仿真模拟目标的点迹，作为自动起始和目标跟踪算法的输入。传统的机械扫描雷达对于非径向运动的目标波束扫过目标的时刻不是一个常数。特别是在多雷达目标跟踪[1-3]中，同一目标被不同雷达观测到的时机几乎是随机的，对多雷达目标跟踪带来了新的挑战。本文通过建立数学模型模拟雷达对目标观测的物理过程[4]，利用计算机仿真技术，建立了一种快速目标点迹模拟方法。

1 模 型

设一机械扫描两坐标雷达在环扫工作方式下以180°/s的转速进行扫描。天线方位与时间t的关系为

A(t)=(A(0)+180t)%360

(1)

其中A(t)表示t时刻时的天线方位。

在t时刻，目标在水平面中的位置是(x(t),y(t))，目标方位B(t)与时间t的关系为

B(t)=natan2(x(t),y(t))

(2)

其中

2 算 法

令式(1)等于式(2)：

(A(0)+180t)%360=natan2(x(t),y(t))

(4)

求解此方程即可得出天线扫过目标的时刻。因为式(4)中包含三角函数，没有一般意义上的解析解，但是可以通过数值计算的方法获得数值解。

2.1 天线旋转模拟

将时间离散化为tk，k=1,2,…，Δtk=t1-t0表示离散时间间隔，将式(1)离散化，可得

A(k+1)=(A(k)+180Δtk)%360

(5)

其中，k和k+1分别表示第k个和第k+1个离散时刻。

设定A(0)后，即可依次计算出各离散时刻天线的方位。

2.2 目标运动模拟

将式(2)离散化，可得

{B(tk)}，k=1,2,…

(6)

2.3 方程(4)求解

令

f(t)=A(t)-B(t)

(7)

将求解方程(4)的问题转化为求解函数f(t)零点的问题。

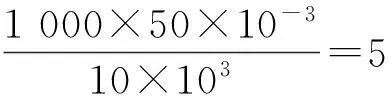
对于在10 km外运动速度且小于1 000 m/s的目标，设Δtk均为50 ms，将式(7)离散化，每50 ms进行一次天线是否扫过目标的判断。当雷达的3 dB波束宽度与50 ms内目标方位的变化相当或更大时，可以将目标方位B(t)在50 ms内近似为线性的，则式(7)在50 ms内也是单调的，从而可以应用二分法[5]计算式(7)零点的数值解。

记无穷小ε=10-2，当前50 ms时间区间的起点和终点分别为tp和tq。用二分法执行以下步骤:

(1) 若|f(tp) |<ε，则在时刻tp天线扫过目标，A(tp)是对应的方位；若|f(tq)|<ε，则在时刻tq天线扫过目标，A(tq)是对应的方位。

(2) 否则：

(a) 若f(tp)和f(tq)的符号相同，则此50 ms内天线不能扫过目标，终止此次判断。

(b) 若f(tp)和f(tq)的符号不同：

(ⅱ) 如果|f(tv) |<ε，则在时刻tv天线扫过目标，A(tv)是对应的方位，退出。

(ⅲ) 否则，若f(tv)与f(tp)的符号相同，则令tp=tv；若f(tv)与f(tq)的符号相同，则令tq=tv。

(ⅳ) 依次执行步骤(ⅰ)～(ⅲ)，直至满足步骤(ⅲ)的条件为止。

在步骤(ⅰ)～(ⅲ)中，每执行一次迭代就在步骤(ⅲ)中将搜索的时间区间长度减小一半。可以证明，在方程(4)有解时，按照以上步骤，一定可以经过有限次的迭代满足步骤(ⅱ)的条件，找到方程(4)的数值解。

实际使用时还可以使用以下两个原则进一步减少计算量：①1个天线周期内天线最多扫过目标1次，②只在上1个天线周期内天线扫过目标的方位附近执行以上步骤。

2.4 点迹信息生成

在方程(4)有解时，在步骤(ⅱ)中获得的数值解tv就是天线扫过目标的时刻。此时目标的距离为

(8)

方位为

natan2(x(t),y(t))

(9)

另外，还需要根据雷达在距离和方位上的观测误差分别在式(8)和式(9)的基础上分别迭加服从正态分布的随机数，才可以获得目标点迹的距离和方位。

目标点迹的距离为

(10)

其中rd是一0均值、标准差为雷达的距离观测误差的随机数。

目标点迹的方位为

natan2(x(t),y(t))+ra

(11)

其中ra是一0均值、标准差为雷达的方位观测误差的随机数。

3 实验及分析

设式(1)中A(0)=0，即天线从正北开始旋转。式(2)中x(0)=80 km，y(0)=60 km，X轴方向的速度vx=-300 m/s，Y轴方向的速度vy=400 m/s。从0时刻起的8 s内的天线和目标的方位如图1所示，其中圆圈表示的就是天线扫过目标的时刻以及对应的方位。

从0时刻起，按Δtk为50 ms将式(7)离散化，并按照以上方法求解。图 1中所示的天线4次扫过目标时刻的主要数据如表1～4所示。

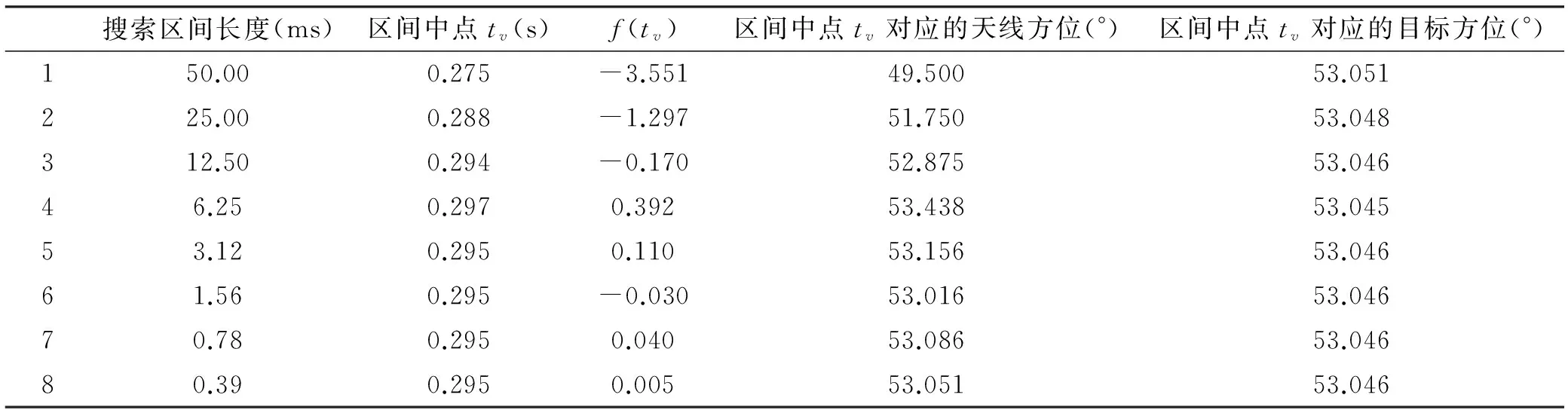
表1 求解天线第1次扫过目标的过程

表2 求解天线第2次扫过目标的过程

表3 求解天线第3次扫过目标的过程

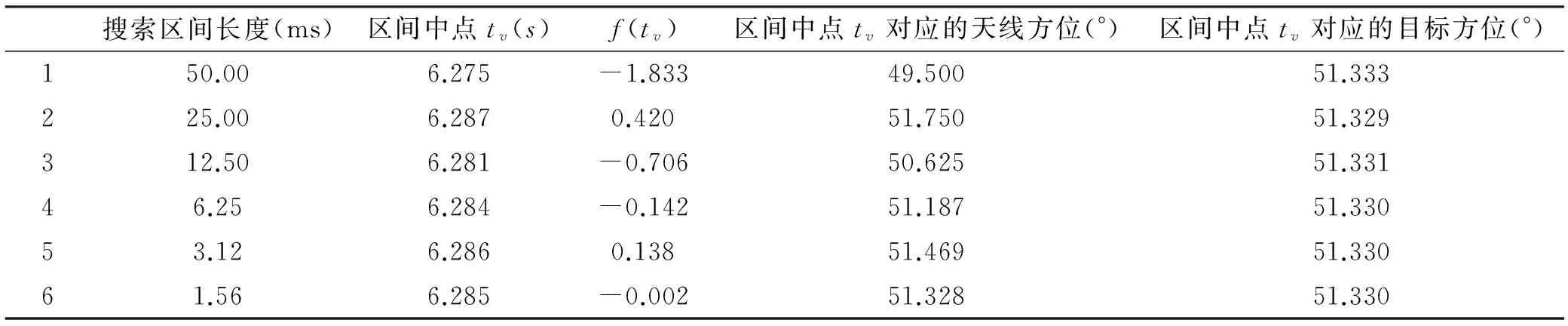
表4 求解天线第4次扫过目标的过程

从表1～4中可以看出，①每一次迭代，搜索区间的长度就缩小一半；②区间中点tv的值f(tv)的符号在无规律地正负交替，以及|f(tv)|不是严格单调下降的，是由步骤(ⅲ)中搜索区间缩短的机制决定的；③只需6～9次迭代|f(tv)|就可以小于10-2，达到步骤(ⅱ)的要求，获得方程(4)的数值解；④随着搜索区间长度的缩小，区间中点tv对应的天线方位和目标方位总体上也越来越接近，并且在搜索终止时两者也趋于一致。

4 结束语

本文将没有解析解的方程求解的问题转化为求解方程零点的数值解的问题，避免了依次模拟天线旋转，可快速定位到天线扫过目标的时刻。再根据目标运动模型，直接生成目标点迹。对于扇扫或者相控阵体制的雷达，根据扫描方式可以建立类似的模型，同样可以快速模拟点迹。

参考文献：

[1] 郭冠斌，方青. 雷达组网技术的现状与发展[J]. 雷达科学与技术，2005(4):193-197, 202.

[2] 唐斌兵. 组网雷达系统中的数据融合[J]. 模糊系统与数学，2001，(3):105-110.

[3] 郭明，许录平. 集中式多雷达系统的数据融合[J]. 雷达与对抗，2003(1):19-22.

[4] 何友，等.多传感器信息融合及应用[M].北京:电子工业出版社，2000.

[5] 郑成德，等. 数值计算方法[M].北京:清华大学出版社，2010.