缺失数据的两个逆伽马分布总体参数的估计与假设检验
罗 倩,周菊玲
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
逆伽马分布是统计学中一种重要的连续概率函数。目前,许多学者在数学、经济学以及可靠性分析领域对逆伽马分布进行了统计研究,取得了丰硕的成果。文献[1]丁新月等在Mlinex损失函数下对逆伽马分布尺度参数进行了Bayes估计;文献[2]张永利对伽马分布及其相关分布性质的一点研究,得出伽马分布和指数分布、卡方分布以及均匀分布等分布之间的关系;文献[3]慈教进做了消费者伽马模型与演化访问行为模型及参数拟合比较;文献[4]杜玲玲等研究了对数伽马分布的尾部性质;文献[5]张永全等基于广义伽马分布的系统可靠性增长预测,预测了系统的未来失效时间。
在对观测数据作统计分析时,常常会遇到数据缺失的情况,对缺失数据的样本的统计分析变得十分重要。对缺失数据样本的研究也有很多,比如文献[6]廖娟芬等对具有缺失数据的多个泊松总体的检验,还对两个总体的分布是否一致的似然比统计量进行了检验;文献[7]王莉等对具有缺失数据的两个0-1分布总体参数的估计和检验;文献[8]赵志文等对具有缺失数据的两个幂分布总体参数的矩估计与检验;文献[9]冯凤飞等对具有缺失数据的两个艾拉姆咖分布总体参数的估计和检验,给出了两总体参数之差的置信区间和假设检验。文献[10]龙兵等对具有缺失数据的两个Pareto分布总体参数的估计与检验。利用极大似然估计方法对具有缺失数据的两个逆伽马分布总体参数的推断和假设检验的相关研究还没有成果,所以文章就此讨论这个问题。
1 极大似然估计及其渐进性质
设观测数据来自两个逆伽马分布总体,其概率密度函数为

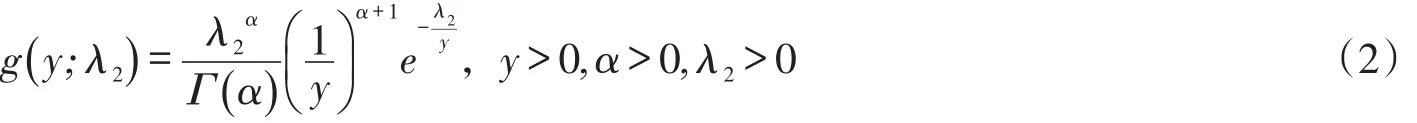
其中α为形状参数,λ1,λ2为尺度参数,文章假设形状参数α已知。
依次对两个总体进行n次独立观测,从每个总体中抽取样本进行观测时,每次以概率P被观测,以概率1-P被丢失。记取自第一个分布总体(1)的观测值为(Xi,δi),i=1,2,…,n.Xi是来自第一个总体的第i个样本寿命.若观测到具体的值时记δi=1,若丢失记δi=0,记来自第二个总体(2)的观测值为(Yi,ηi),i=1,2,…n.Yi是来自第二个总体的第i个样本寿命,若可观测到具体的值时记ηi=1,若丢失记为ηi=0。
下面对未知参数λ1用极大似然估计,取上面一组观测值(Xi),δi,i=1,2,…,n,有如下的似然函数为:
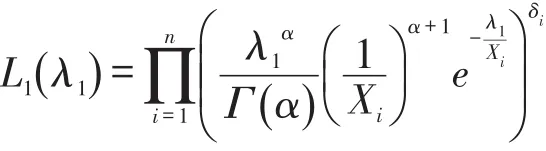
将似然函数取对数,则:
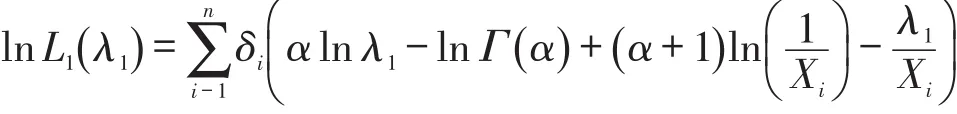
两边对λ1求导为:
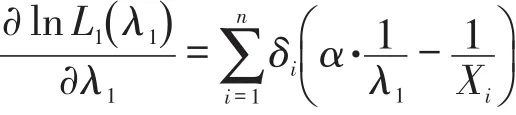

同理,取来自第二个分布总体的一组样本观测值(Yi,ηi),i=1,2,…,n.能得出参数λ2的极大似然估计为:

有了参数λ1的极大似然估计,下证相合性与渐进正态性。
定理1.1 来自伽马分布总体(1)的一组观测值(Xi,δi),i=1,2,…,n.则
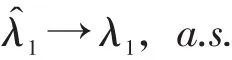
证明:由于{Xiδi,1≤i≤n}为独立同分布的随机变量,则由强大数定律可知
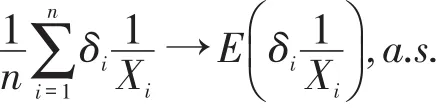
其中
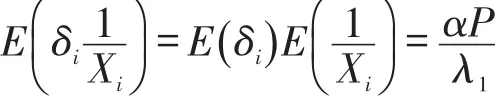
同理
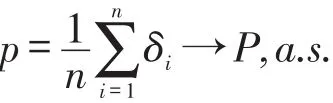
即

引理1.1[11]记Tn=(T1n,…,Tkn)T,θ=(θ1,…,θk)T,设
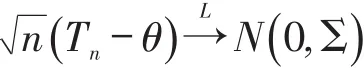
其中Σ=(σij)k×k.又设g(t1,…,tn)对各ti有连续的偏导数,则当n→∞时,有
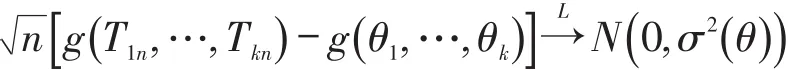

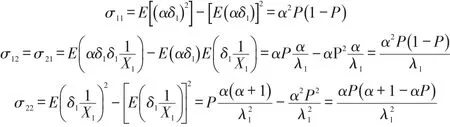
令
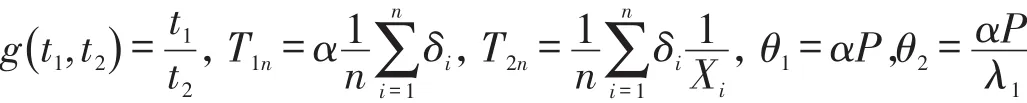
则
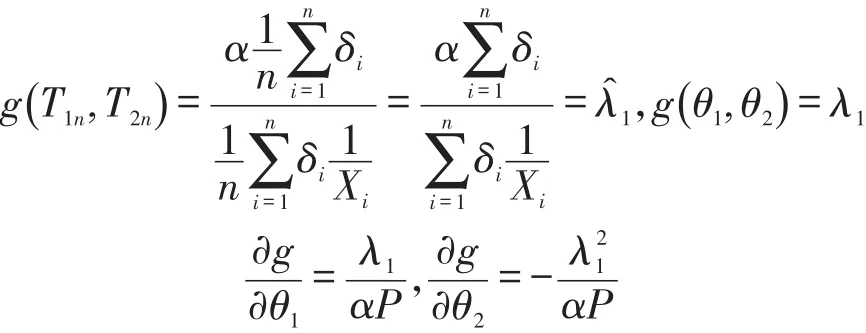
所以由引理1.1可得到
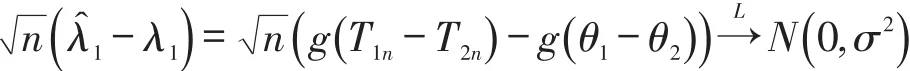
其中
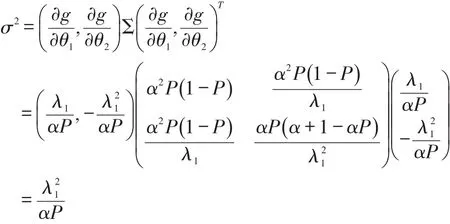
所以
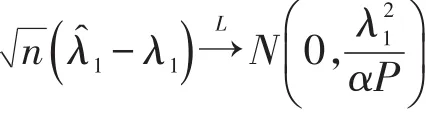
2 两尺度参数之差的区间估计及参数之比的假设检验
在实际问题中,常常会比较两个参数的大小,这样就可以归结到参数之差的置信区间问题,这样可以得到如下的定理。
定理2.1 在前面的记号下,若是(3)式所给出的λ1的极大似然估计,是(4)式所给出的λ2的极大似然估计。若0<μ<1,则λ1-λ2的置信水平为1-μ的近似置信区间为
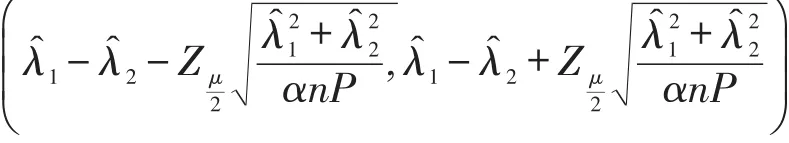
其中Zμ为标准正态分布的μ下分位数。
所以
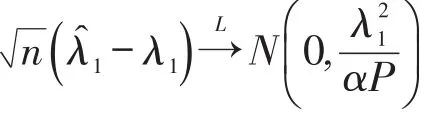
同理
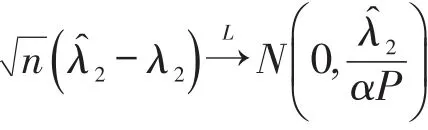
又因为相互独立,所以

所以λ1-λ2的置信水平为1-μ的置信区间为
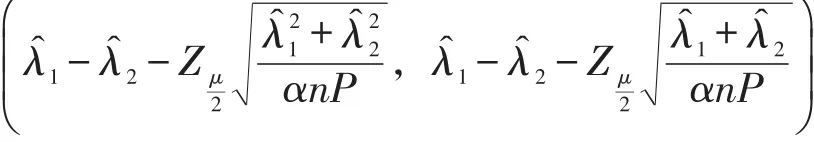
(1)对于假设检验问题
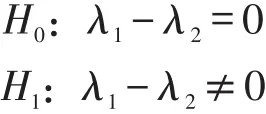
当H0成立时
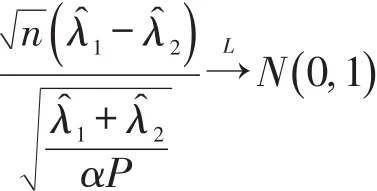
对于给定的显著性水平μ( )0<μ<1,检验的拒绝域为
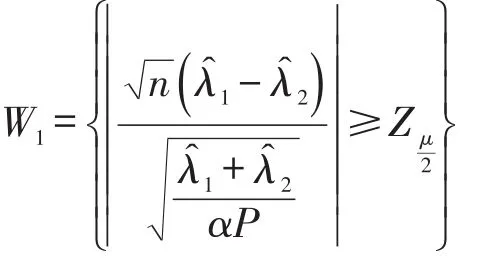
(2)对于假设检验问题

同样地,对于给定的显著性水平μ( )0<μ<1,检验的拒绝域为
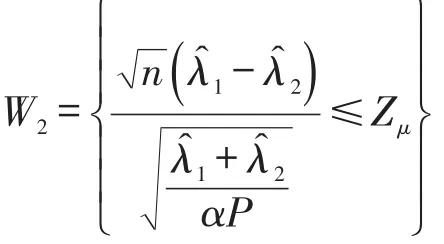
(3)对于假设检验问题

同样地,对于给定的显著性水平μ( )0<μ<1,检验的拒绝域为
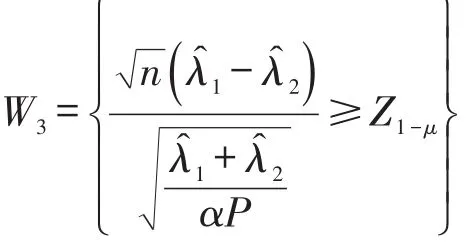
3 结语
在实际问题中,通过对具体数据随机抽取观测数据,对总体参数估计与假设检验,得到参数估计的置信区间,能更好的得到统计分析的可靠度。
参考文献:
[1]丁新月,徐美萍.Mlinex损失函数下逆伽马分布尺度参数的Bayes估计[J].广西师范学院学报(自然科学版),2014,32(3):61-64.
[2]张永利.关于伽马分布及相关分布性质的一点研究[J].大学数学,2012,28(3);135-140.
[3]慈教进.消费者伽马分布模型与演化访问行为模型及参数拟合比较[J].统计与决策,2014,(24):69-71.
[4]杜玲玲,陈守全.对数伽马分布的尾部性质[J].西南大学学报(自然科学版),2016,38(1):85-89.
[5]张永全,郭建英,等.基于广义伽马分布的系统可靠性增长预测[J].北京理工大学学报,2010,30(9):1131-1134.
[6]廖娟芬,李春红.具有缺失数据的多个泊松总体的检验[J].数学统计与管理,2014,33(4):642-646.
[7]王莉,郭鹏江,等.具有缺失数据的两个0-1分布总体参数的估计和检验[J].温州大学学报(自然科学版),2012,33(1):6-10.
[8]赵志文,杨慧超,等.具有缺失数据的两个幂分布总体参数的矩估计和检验[J].吉林师范大学学报(自然科学版),2016,37(2):63-67.
[9]冯凤飞,龙兵.具有缺失数据的两个艾拉姆咖分布总体参数的估计与检验[J].岭南师范学院学报,2016,37(3):32-38.
[10]龙兵,王秋节,等.具有缺失数据的两个Pareto分布总体参数的估计与检验[J].贵州师范大学学报(自然科学版),2016,33(1):9-12.
[11]赵志文,M.S.Abdalroof,等.定时截尾下具有缺失数据的两个Rayleigh分布总体参数的估计与检验[J].吉林大学学报(理学版),2013,51(6):1090-1094.

