一种新的基于小波变换的图像边缘检测方法
王思雨,吐尔洪江·阿布都克力木,阿斯古丽·艾合麦提
(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)
人类传递信息的主要媒介是语言和图像。根据统计分析,在人类接受的各种信息中视觉信息占80%,所以,图像信息是十分重要的信息传递媒体和方式。信号和图像中存在着各种噪声,各种传感器所获得的图像信息一般都含有Gauss噪声和非Gauss噪声,图像中的噪声对图像分析、分类和识别影响很大[1]。近年来,小波变换作为新的一种分析方法在图像处理中得以广泛的应用[2],能在时间和频率域内同时进行分析,使能量能集中于较少的小波变换系数。另外,小波的多分辨率分析结构能允许应用匹配每个频带的统计性和人的视觉特征的有效编码方法,成为图像编码的强有力工具。它已成为机器视觉研究领域最活跃的课题之一,在工程应用中占有十分重要的地位[3]。
文章设计了复系数全通滤波器并用其对复杂内容的图像进行增强,再对增强后的图像进行边缘检测。实验结果显示,应用文章设计的滤波器可有效地克服图像进行边缘检测过程中噪声对其的影响,边缘检测之后的效果明显优于db(6)小波滤波器和传统算子对图像进行处理后的效果。
1 小波变换与Mallat算法
小波变换是Fourier变换的变种,其目的是为了使之适用于局部变化的处理。在小波变换中,连续变换系数WTv(a,b)=[v(t),ψa,b(t)]主要依赖于信号在 [b-aΔψ,b+aΔψ]区间中的情况,时间宽度是 2aΔψ,该时间宽度是随着尺度a变化而变化的,其中,所以小波变换具有时间局部分析能力[4]。由于小波变换在实际运算中需要计算大量的系数,工作量巨大,下面介绍一种快速算法——Mallat算法。
定义1 若υ(k)为信号的离散采样数据,如果,则信号分解的Mallat算法为

式中N为离散采样数据个数;h,g为滤波器脉冲响应,即分解各列滤波器系数;cj,k为υ(k)在2j分辨率下的逼近,称为信号的低频部分系数;dj,k为υ(k)在2j分辨率下的离散细节,称为信号的高频部分系数。
如果从j=0层开始,经过J层分解后得到的是c-J,d-J,d-J+1,…,d-1。
信号重构的Mallat算法如下:
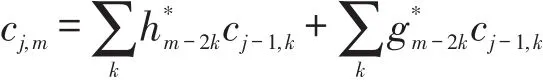
式中和分别为hm-2k和gm-2k的共轭,实际上也就是重构各列滤波器组的系数。
Mallat算法中不需要知道尺度函数ϕ(t)和小波函数ψ(t)的具体结构,仅通过滤波器系数h和g就可以实现信号的分解与重构,由此可见滤波器在Mallat算法中的重要性[4]。
2 复系数全通滤波器的构造
定义2 能够使所有频率分量无衰减的通过的系统称为全通系统,也称全通滤波器。
对于N阶全通滤波器,有理传递函数A(z)可以表示为如下形式:
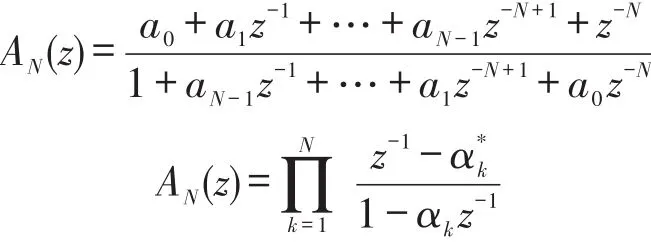
其中αk为极点,α*k表示αk的共轭。
当AN(z)乘一个复常量β,即,A'N(z)就叫做复系数全通滤波器。
命题1 若A(z)=A'N(z)是一个N阶复系数全通滤波器,)的滤波器系数是A(z)的复共轭,则有滤波器组{H(z),G(z)}:

式中,低通滤波器H(z)和高通滤波器G(z)的系数是实系数。
命题2 由实系数的二通道仿酉滤波器组{H(z),G(z)}能够获得实值正交小波滤波器,其中H(z)和G(z)所满足的正交条件是[4]:

复系数全通滤波器A(z)的传递函数能够表示为:

其中A(z)的阶数是N=2N1+4N2,β是复常量,|β|=1,可以令β=eiη或者,将(3)式展开得到,当为奇数时:


定理1 若A(z)的传递函数可以写成(4)和(5)式的形式,则A(z)的系数an可以由如下公式给出:
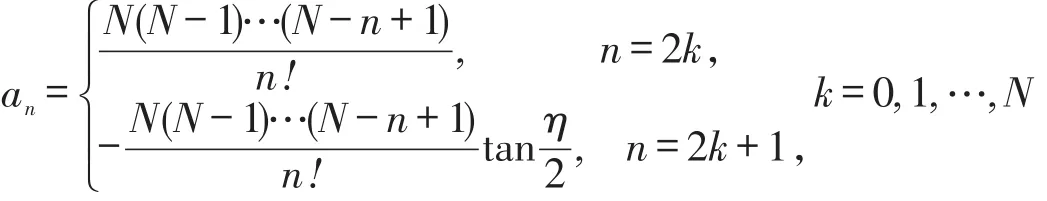

表1 A(z)的系数
将表中数据代入(1)、(4)和(5)式可得:

3 算法实现流程
文章提出的新的基于小波变换的图像边缘检测方法共包括小波分解、应用构造的复系数全通滤波器进行滤波和边缘检测三个部分,具体流程如图1所示。

图1 算法实现流程图
4 实验结果及分析
文章实验所选用的实验图像是信息量较大的Baboon图,分别用文章构造的小波滤波器、db(6)小波滤波器、Sobel算子、Prewitt算子和Roberts算子对其进行处理。实验效果如图2,其中实验结果图(a)为原图、(b)为文章构造的小波滤波器检测结果、(c)为db(6)小波滤波器检测结果、(d)为Sobel算子检测结果、(e)为Prewitt算子检测结果、(f)为Roberts算子检测结果。

图2 实验效果图
从图2可知,文章构造的小波滤波器对应的小波变换方法在图像边缘检测效果上明显优于db(6)小波滤波器对应的小波变换方法和其它四种常用算子方法,尤其是文章方法可以将狒狒脸部细节检测出来,并且轮廓清晰。图(c)虽然可以体现出狒狒脸部的大部分轮廓,但是狒狒鼻子上的细节之处体现不出来;图(d)虽边缘定位精度高,但容易丢失部分边缘几乎没有检测到狒狒的脸部细节;图(e)和(f)虽然检测处的细节之处有体现,但是效果不明显。
由于实际生活中人们获取到的图像种类繁多,文章构造的小波滤波器对应的小波变换方法不能将其全部进行实验对比,另外文章中构造的小波滤波器对应的小波变换方法在图像边缘检测效果上不够精化,这也正是以后研究的重要方向。
参考文献:
[1]YAN Jing-wen,QIAN Shen-en.The Analy sis and Development of Theory Method in N on-Gaussion Environments[A].The Third Proceeding of National Sy mposium on Developments of Microwave Compatibility[C].Bei jing:Bei jing Broadcasting Instiute Press 1996.
[2]孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005:31-58.
[3]张德丰.MATLAB数字图像处理[M].北京:机械工业出版社,2012:268-292.
[4]吐尔洪江·阿布都克力木.小波信号处理基础[M].北京:北京邮电大学出版社,2014:6-163.

