核磁共振陀螺静磁系统端口漏磁抑制技术

李 攀，刘元正，王继良

（中航工业西安飞行自动控制研究所，西安 710065）

核磁共振陀螺（Nuclear Magnetic Resonance Gyroscope，NMRG）是一种利用核磁共振原理工作的全固态陀螺仪。它没有运动部件，性能由原子材料决定，理论上动态测量范围无限，综合运用了量子物理、光、电磁和微电子等领域中的技术，是未来陀螺仪发展的新方向[1-7]。

原子自旋可以在惯性参考系中保持其初始指向，类似于传统机械陀螺中的转子，所以原子自旋也可以用于敏感转动。欧美国家从20世纪60年代就已经开始研究核磁共振陀螺，Litton公司和 Singer-Kearfott公司在1979年分别开发出了核磁共振陀螺原型机，均达到了导航精度[8]。虽然结果鼓舞人心，但核磁共振陀螺项目仍在其潜力被完全认识前取消了。项目的停止主要归因于同期激光陀螺技术的发展，当时激光陀螺技术被认为更有前途。

进入21世纪以来，微型原子器件的显著进步证实了原子MEMS的可行性，为核磁共振陀螺的发展迎来的曙光[9-10]。2005年，美国国防先进研究计划局（DARPA）提出了导航级集成微陀螺（NGIMG）概念，在定位、导航和授时微技术（Micro-PNT）项目中对美国 Northrop Grumman公司的核磁共振陀螺研究给予了支持[11]。到2012年美国Northrop Grumman公司实现了导航级核磁共振微陀螺[12]，随机游走达到0.01 (°)/√h，零偏稳定性达到 0.05 (°)/h，满量程速率大于 500 (°)/s，刻度因子稳定性＜25×10-6，成为目前世界上达到导航级精度中体积最小的陀螺，标志着高精度、小体积陀螺技术领域取得了突破性进展。

核磁共振陀螺利用检测磁场中原子核自旋进动频率的改变确定载体角速度。陀螺所涉及的磁场包括纵向静态磁场和横向振荡磁场，原子核自旋绕静磁场进动，振荡磁场频率与原子核进动频率相同。在进行陀螺设计时，必须保证静态磁场纵向分量在气室范围内均匀分布，横向分量近似为零，振荡磁场横向分量在气室范围内均匀分布，纵向分量近似为零。从陀螺原理可以看出，核磁共振陀螺的陀螺精度与静磁场的均匀性、稳定性密切相关。

为防止外部磁场对陀螺的干扰，核磁共振陀螺需要磁屏蔽。核磁共振陀螺静磁场通常由亥姆霍兹线圈或螺线管产生，这两种结构均存在漏磁，在长期工作过程中一方面会因为磁力线在磁屏蔽材料表面反射形成杂散磁场，另一方面会导致磁屏蔽罩长期磁化，并最终干扰陀螺精度。

1 静磁场系统漏磁计算

目前，在核磁共振领域得到工程应用的均匀静磁场产生方案一般有两种[13-15]：亥姆霍兹线圈和螺线管。这里我们将亥姆霍兹线圈看作两匝的疏绕螺线管，从而只讨论螺线管一个方案。

1.1 载流环形线圈的磁场

载流环形线圈如图1所示。以线圈中心为坐标原点建立直角坐标系，z轴与线圈平面垂直，电流I以逆时针方向绕z轴旋转。根据毕奥-萨伐尔-拉普拉斯定律，任一电流元Idl在点P形成的磁场可以表示为

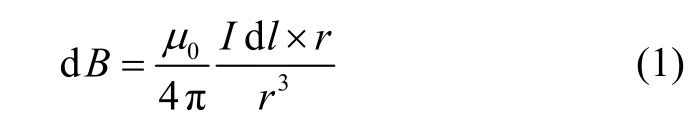
其中，r为元电荷指向点P的矢量，μ0为真空电导率。

可以得到P点的磁感应强度：

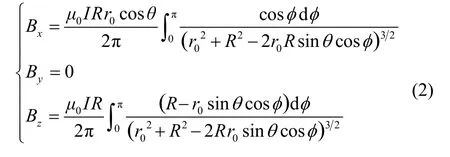
图1 环形电流磁场Fig.1 Ring current magnetic field

1.2 通电螺线管的轴向磁场

通电螺线管的磁场可以近似看作一系列圆形线圈磁场的叠加。

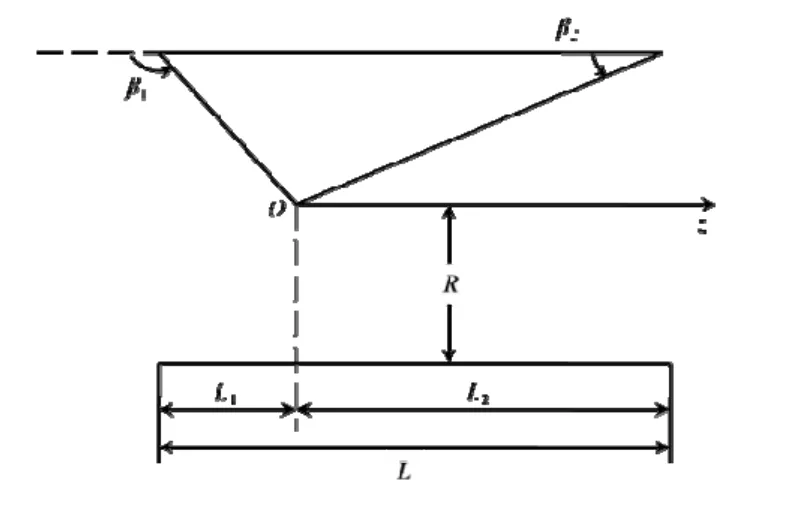
图2 螺线管轴上的磁场Fig.2 Magnetic field on the solenoid axis

令螺线管长为L，半径为R，单位长度的匝数为n，电流强度为I，可以得到螺线管在原点产生的磁感应强度为

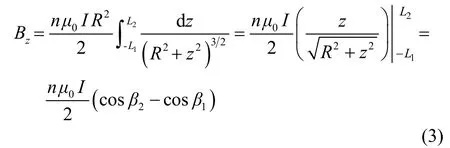
其中，β1和β2如图2所示。

1.3 螺线管的离轴磁场

下面我们考虑螺线管的漏磁，即螺线管外的离轴磁场。从式(4)得到载流线圈的离轴磁场为

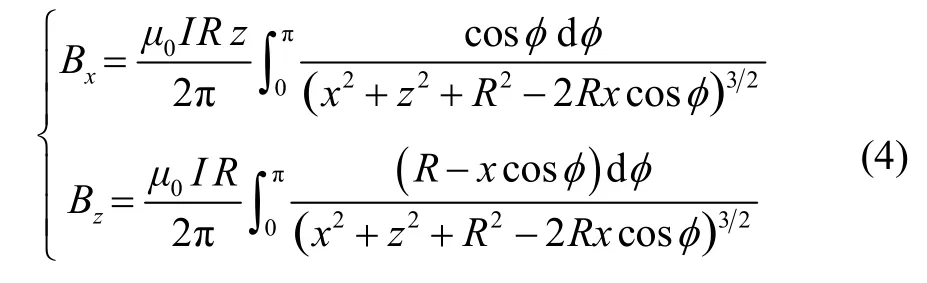
其中，x、z为离轴点到线圈中心的径向和轴向距离。将螺线管的每个线圈分别进行计算并进行叠加就可以得到螺线管的离轴磁场大小。

为便于计算，采用梯形公式对式(8)进行近似，有其中，ak=0+kh=kh，k=1,2,…,N−1，h=(π−0)/N=π/N。

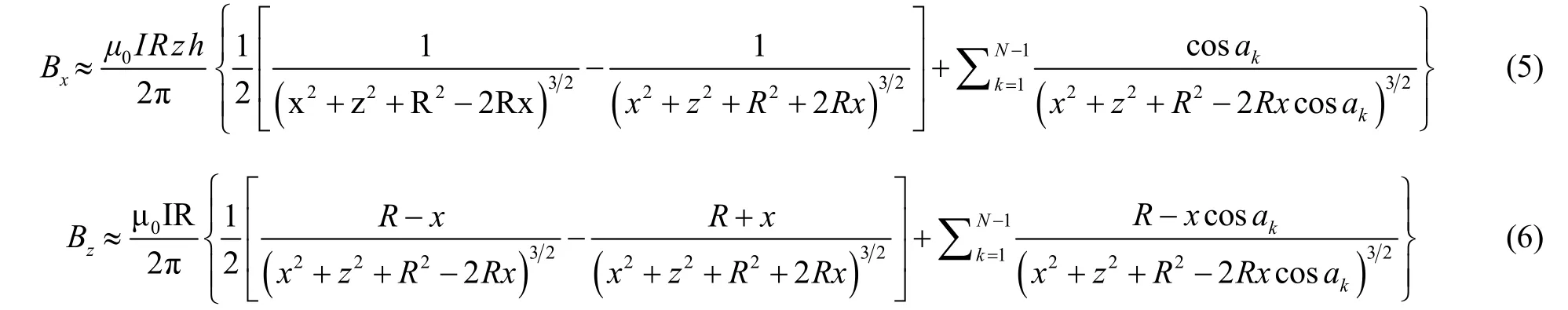
设计核磁共振陀螺螺线管为半径R=25 mm，绕组长度L=50 mm，绕组匝数n=50，通电电流I=0.2 A，其轴向磁场如图 3所示。定义磁场非均匀性指标δ=std(B)/mean(B)，取气室尺寸大小计算δ=0.01。

螺线管端口沿径向的磁场分布如图4所示。

图3 传统螺线管的轴向磁场分布Fig.3 Axial magnetic field distribution of conventional solenoid

图4 传统螺线管端口沿径向磁场分布Fig.4 Radial magnetic field distribution at the conventional solenoid port

端口处的离轴磁场可以分解为Bz和Bx两个部分，且Bx起主要作用，所以减小离轴磁场主要是要消除径向磁场Bx。

2 核磁共振陀螺静磁系统漏磁抑制

经过简单分析可以发现，通过改变静磁线圈的长径比可以有效减小端口漏磁，比如减小线圈尺寸或增加线圈长度，但在核磁共振陀螺使用中却受到了限制。由于核磁共振陀螺是一种微陀螺，静磁线圈的直径受到其内部陀螺结构的限制，而长度受到了陀螺体积的限制。总的来说，通过改变静磁线圈尺寸来抑制端口漏磁的效果有限。此外，还需要考虑磁场均匀性的要求，因为核磁共振陀螺会严格限制静磁系统的磁场均匀性，核磁共振陀螺的陀螺精度与静磁场的均匀性、稳定性密切相关。所以我们需要一种体积小、结构简单且不影响静磁系统磁场均匀性的漏磁抑制技术。

可以参考无矩线圈使用双层螺线管结构来抑制离轴磁场，该方法通过几组子线圈以一定的几何结构安装方式，并通过各组子线圈一定的线圈匝数和一定的电流方向，使线圈外部的磁场急速衰减，线圈的磁矩为零。这种螺线管具有十分突出的优点：在工作时对一定距离外的环境不会产生磁干扰、不会磁化较临近的磁性物质等。

此外，双层螺线管还有另外一个优点。从图3中可以看出，普通螺线管沿中心轴的磁场分布表现出两端小、中间大的特征，这也是影响磁场均匀性的主要因素。而双层螺线管通过在外层施加一个反向磁场在一定程度上对磁场中心进行了平滑，所以可以通过合理的结构设计来提高磁场均匀度。

无矩线圈的外形尺寸在结构上满足下列关系[16]：

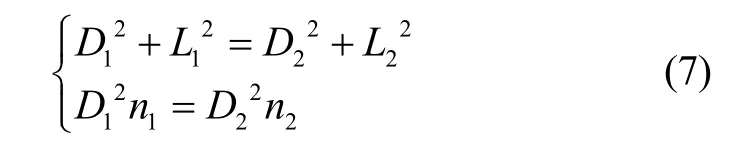
式中：D1、D2为内外螺线管的直径，L1、L2为内外螺线管的绕组长度，n1、n2为内外螺线管绕组匝数。

2.1 初步设计

参考无矩线圈的结构，初步设计双层螺线管为D1=50 mm、D2=60 mm、L1=50 mm、L2=37.42 mm、n1=50、n2=35、I=0.66 A，尺寸严格满足无矩线圈结构，内外螺线管通电电流方向相反，产生的轴向磁场如图5所示。与设计要求相近，取气室尺寸大小计算磁场非均匀性指标δ=3.19×10-4，磁场均匀性显著提高。

双层螺线管端口沿径向的磁场分布如图6所示。

可以看出，与普通螺线管相比：对于Bz，双层螺线管在D＞96.54 mm区域漏磁优于普通螺线管；对于Bx，双层螺线管在D＞65.58 mm区域漏磁优于普通螺线管。令标量B=(Bz2+2Bx2)0.5，所得结果如图7所示。

由图7可以看出，双层螺线管在D＞92.50 mm区域漏磁优于普通螺线管，远大于双层螺线管的外线圈直径D2（60 mm）。由于核磁共振陀螺需要严格限制尺寸大小，磁屏蔽罩的内径仅略大于静磁场线圈，在此范围内使用无矩线圈对静磁系统产生的漏磁几乎没有抑制效果。

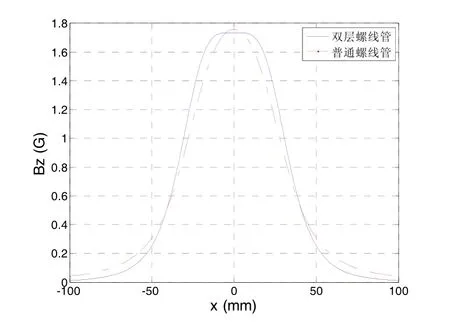
图5 双层螺线管沿轴向的磁场分布Fig.5 Axial magnetic field distribution of double-layer solenoid

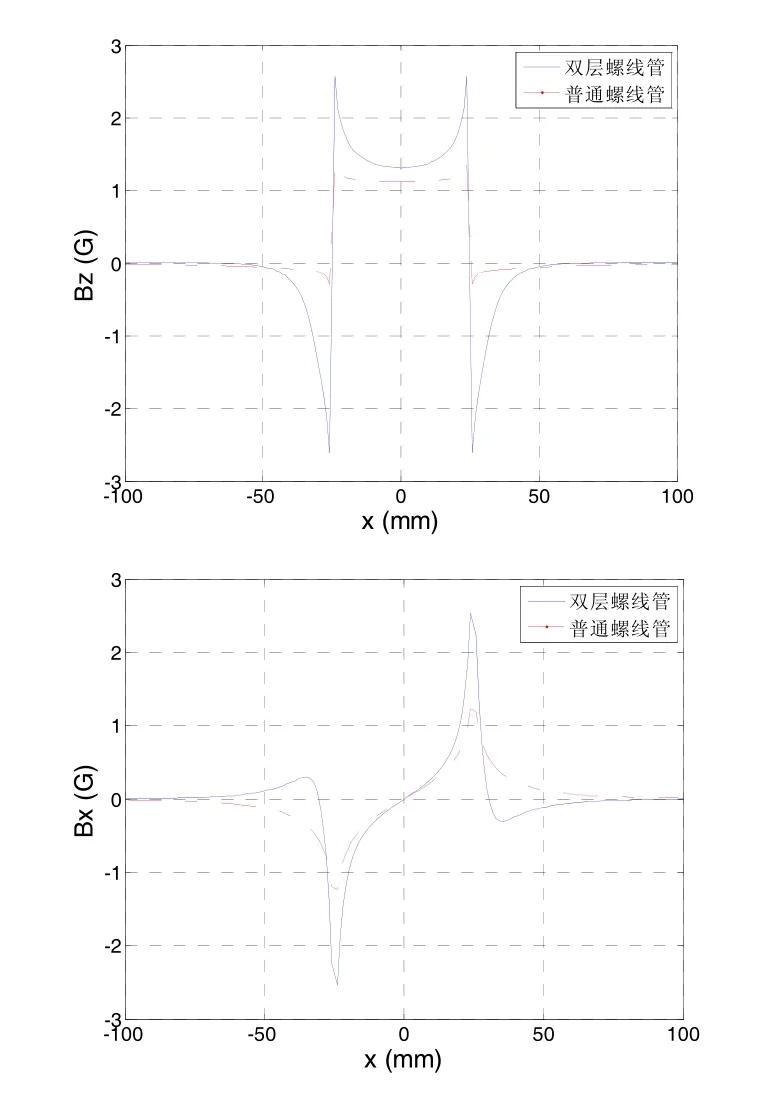
图6 双层螺线管端口沿径向矢量磁场分布Fig.6 Radial vector magnetic field distribution at the double-layer solenoid port

图7 双层螺线管端口沿径向标量磁场分布Fig.7 Radial scalar magnetic field distribution at the double-layer solenoid port

2.2 参数分析

下面将通过参数分析来确定双层螺线管结构参数对线圈漏磁的影响，从而通过优化结构参数来进一步提升双层螺线管的性能。

选用参数D1=50 mm、D2=60 mm、L1=50 mm、L2=37.42 mm、n1=50、n2=35、I=0.66 A，固定其它参数，改变其中一个以确定双层螺线管结构参数对性能的影响。判断指标采用内螺线管端口沿径向磁场分布绝对值的平均值。

● 外螺线管直径D2

外螺线管直径D2对双层螺线管漏磁的影响如图8所示。

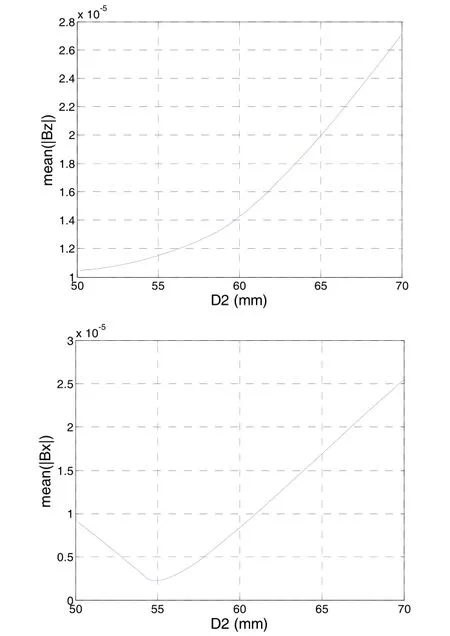
图8 外螺线管直径D2对双层螺线管漏磁的影响Fig.8 Influence of diameter D2 of external solenoid on magnetic flux leakage of double-layer solenoid port

从图8中可以看出：对于Bz，双层螺线管的漏磁随着D2的增加而增加；对于Bx，则存在极小值点，此时D2=54.8 mm。

● 外螺线管长度L2

外螺线管长度L2对双层螺线管漏磁的影响如图 9所示。从图9中可以看出：对于Bz，双层螺线管的漏磁随着L2的增大而减小；对于Bx，则存在极小值点，此时L2=39.03 mm。

图9 外螺线管长度L2对双层螺线管漏磁的影响Fig.9 Influence of length L2 of external solenoid on magnetic flux leakage of double-layer solenoid port

● 外螺线管匝数n2

图10 外螺线管匝数n2对双层螺线管漏磁的影响Fig.10 Influence of number of turns n2 of external solenoid on magnetic flux leakage of double-layer solenoid port

外螺线管匝数n2对双层螺线管漏磁的影响如图10所示。从图10中可以看出：对于Bz，存在极小值点，此时n2=33；对于Bx，存在极小值点，此时n2=28。综合考虑，最优点为n2=28。

2.3 参数优化

从上述分析可以看出，外螺线管直径D2、外螺线管长度L2、外螺线管匝数n2都会影响对静磁系统端口漏磁的抑制效果，我们可以通过回归分析的方法建立上述参数与静磁系统端口漏磁抑制之间的回归关系，同时兼顾静磁系统小体积、磁场高均匀的要求。

为降低计算量并提高回归精度，并考虑到使用简单的一次回归正交设计并不能得到满意的结果，采用最优近似饱和设计进行二次回归。取外螺线管直径D2、外螺线管长度L2、外螺线管匝数n2作为四因子，采用最优近似饱和设计（R311D）进行回归设计，各因子的编码自变量(xi)的编码水平j和实际自变量(zi)的实际水平如表1所示。

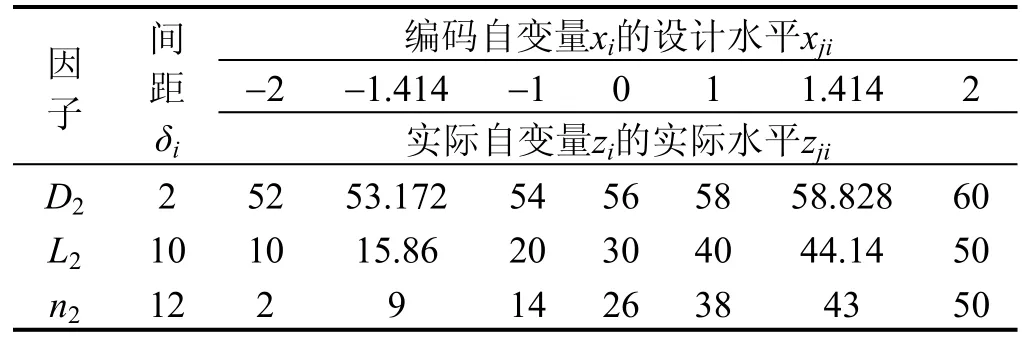
表1 最优近似饱和设计试验因子及水平Tab.1 Optimal approximation saturation design experimental factors and levels

对于本设计来说：外线圈直径D2需要大于内线圈直径D1，但也需要考虑到实际安装的最大尺寸；外线圈长度L2需要小于内线圈长度；同时，外线圈匝数最少2匝，考虑到常规导线的直径，最大不超过50匝。实施水平间距δi为：

设计水平j对应的实际水平为：

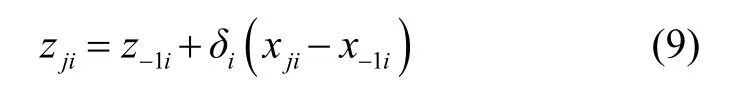
具体数值如表1所示。

使用Matlab进行仿真计算。对于各组参数，改变电流以使螺线管在气室范围内产生的磁场大小归一化以减小误差，并以磁屏蔽罩区域漏磁场标量B的均值（Gauss）为判定条件，兼顾磁场均匀性指标δ，得到结果如表2所示。

使用下列模型进行二次回归：

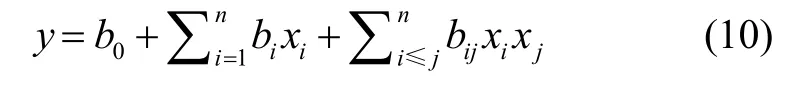
式中，n为自变量的数目，b0为回归方程的常数项，bi为一次项的偏回归系数，bij为二次项的偏回归系数。

使用Minitab进行多轮数学回归。若数学回归的结果中有系数未达到显著水平（p＜0.05），将其并入误差项继续进行回归，直到得到最终的回归方程。

对于磁场参数y1（磁屏蔽罩区域漏磁场标量B的均值），从最终回归的方差分析表（表3）可以看出，回归达到极显著水平（F＞F0.01(5,5)=10.97），回归方程的复相关系数Rsq=0.969。偏回归t检验中，只有b12达到显著水平（p＜0.05），其余系数均达到极显著水平（p＜0.01），如表4所示。

表2 试验方案及结果Tab.2 Experimental scheme and results

表3 试验方差分析Tab.3 Analysis of variance

表4 偏回归系数b的t检验Tab.4t test of partial regression coefficient b

回归方程为：

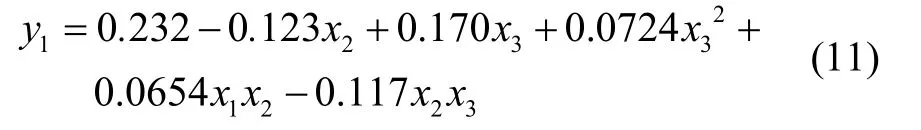
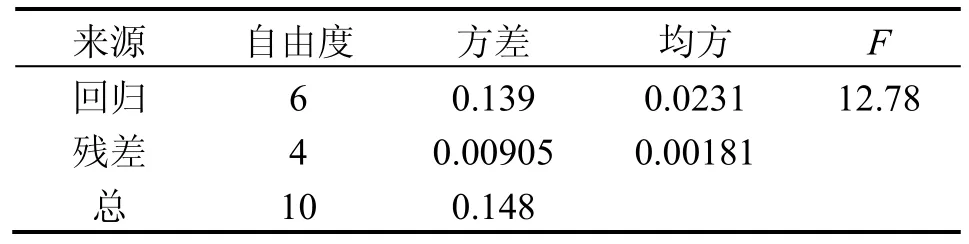
表5 试验方差分析Tab.5 Analysis of variance

对于磁场参数y2（即磁场均匀性指标δ），从最终回归的方差分析表（表5）可以看出，回归达到极显著水平（F＞F0.05(6,4)=14.54），回归方程的复相关系数Rsq=0.939。偏回归t检验中，只有b23达到极显著水平（p＜0.01），其余系数达到显著水平（p＜0.05），如表6所示。

表6 偏回归系数b的t检验Tab.6t test of partial regression coefficient b

回归方程为：

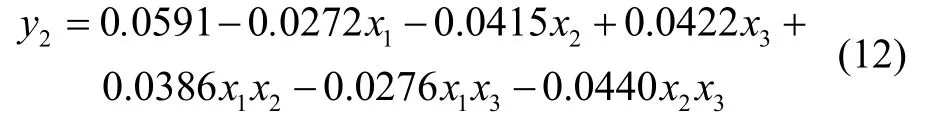
考虑到

可得：

即：

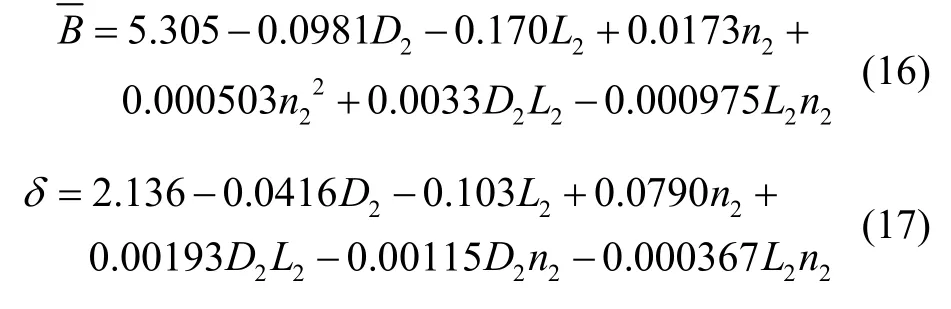
结合回归方程综合考虑漏磁大小和磁场均匀性指标，取D=54 mm、L=43 mm、n=38，对应(-1, 1.3, 1)水平。回归结果为=0.077G，δ=5.19×10-3。Matlab仿真结果为=0.091G，δ=6.41×10-4，磁场非均匀性指标比回归结果更小一些。

此时螺线管产生的轴向磁场如图11所示。可以看出中心区域磁场均匀性有明显改善。端口漏磁如图 12所示。由图 12中可以看出，优化后的双层螺线管在D＞61.72mm 区域端口漏磁明显优于普通螺线管，在1.5倍螺旋线管直径（差不多能涵盖整个磁屏蔽罩）范围内，漏磁较普通螺线管平均减小 45.4%，对静磁系统的漏磁起到了有效的抑制作用，可以满足核磁共振陀螺的使用需求。

图11 优化后的双层螺线管沿轴向的磁场分布Fig.11 Axial magnetic field distribution of the optimized double-layer solenoid

图12 优化后的双层螺线管端口沿径向的标量磁场分布Fig.12 Radial scalar magnetic field distribution at the optimized double-layer solenoid port

3 结 论

作为一种新型微型陀螺仪，随着MEMS技术和微型原子器件的发展，核磁共振陀螺仪有望在中低精度导航和制导领域得到应用，其潜在应用方向包括小型飞行器、无人飞行器、无人水下潜艇、地面车辆、战术导弹等。美国陆军计划从2013年开始进行将核磁共振陀螺纳入单兵作战平台的实验和测试工作[17]。

本文从核磁共振陀螺静磁场分布的理论分析出发，通过数学计算和计算机仿真，分析和研究了静磁系统的端口漏磁，并对静磁系统进行了优化设计。设计的核磁共振陀螺静磁系统端口漏磁在1.2倍螺线管直径范围内较传统方案平均减小 45.4%，满足了核磁共振陀螺的使用需求。该工作为核磁共振陀螺仪设计和制造提供了一定的理论依据和参考价值。

参考文献（References）：

[1]程向红, 陈红梅, 周雨青, 等. 核磁共振陀螺仪分析及发展方向[J]. 中国惯性技术学报, 2006, 14(6): 86-90.Cheng X H, Chen H M, Zhou Y Q, et al. Review of nuclear-magnetic resonance gyroscopes[J]. Journal of Chinese Inertial Technology, 2006, 14(6): 86-90.

[2]陈红梅, 程向红, 员亚利. 低温超导核磁共振陀螺仪模型[J]. 中国惯性技术学报, 2008, 16(2): 228-232.Chen H M, Cheng X H, Yuan Y L. Model of nuclearmagnetic resonance gyroscopes with cryogenic superconductor[J]. Journal of Chinese Inertial Technology,2008, 16(2): 228-232.

[3]李攀, 刘元正, 王继良. 核磁共振微陀螺的现状与发展[J]. 微纳电子技术, 2012, 49(12): 769-785.Li P, Liu Y Z, Wang J L. Current status and development of nuclear magnetic resonance microgyroscope[J]. Micronanoelectronic Technology, 2012, 49(12): 769-785.

[4]严吉中, 李攀, 刘元正. 原子陀螺基本概念及发展趋势分析[J]. 压电与声光, 2015, 37(5): 810-817.Yan J Z, Li P, Liu Y Z. Analysis of the basic concept and the development tendency of atomic gyroscopes[J].Piezoelectrics & Acoustooptics, 2015, 37(5): 810-817.

[5]刘丽君, 席在荣. 原子核自旋陀螺仪的基本原理[J]. 系统科学与数学, 2012, 32(10): 1308-1317.Liu L J, Xi Z R. The principle of atomic spin gyroscope base on a comagnetometer[J]. Journal of Systems Science and Mathematical Sciences, 2012, 32(10): 1308-1317.

[6]Fang J C, Qin J. Advances in atomic gyroscopes: A view from inertial navigation applications[J]. Sensors, 2012,12(5): 6331-6346.

[7]Fang J C, Qin J, Wang S A, et al. Atomic spin gyroscope based on129Xe-Cs comagnetometer[J]. Chinese Science Bulletin, 2013, 58(13): 1512-1515.

[8]Kitching J, Knappe S, Donley E A. Atomic sensors – a review[J]. IEEE Sensors Journal, 2011, 11(9): 1749-1758.

[9]Knappe S, Shah V, Schwindt P, et al. A microfabricated atomic clock[J]. Appl Phys Lett, 2004, 85(9): 1460-1462.

[10]Schwindt P, Knappe S, Shah V, et al. Chipscale atomic magnetometer[J]. Appl Phys Lett, 2004, 85(9): 6409-6411.

[11]Larsen M, Bulatowicz M. Nuclear magnetic resonance gyroscope for DARPA’s micro-technology for positionning, navigation and timing program[R]. USA: Northrop Grumman, 2012.

[12]Meyer D, Larsen M. Nuclear magnetic resonance gyro for inertial navigation[J]. Gyroscopy and Navigation, 2014,5(2): 75-82.

[13]Eklund E J. Microgyroscope based on spin-polarized nuclei[D]. USA: University of California, 2008.

[14]李攀, 刘元正, 王继良. 核磁共振陀螺多层磁屏蔽系统优化设计[J].中国惯性技术学报, 2016, 24(3): 383-389.Li P, Liu Y Z, Wang J L. Optimization design of multilayer magnetic shield for nuclear magnetic resonance gyroscopes [J]. Journal of Chinese Inertial Technology, 2016,24(3): 383-389.

[15]Kornack T W. A test of CPT and Lorentz symmetry using a K-3He co-magnetometer[D]. USA: Princeton University,2005.

[16]程华富. 交变微弱磁场标准研究[J]. 水雷战与舰船防护, 2009, 17(1): 9-12.Cheng H F. Research on alternating weak magnetic field standards[J]. Mine Warfare & Ship Self-Defence, 2009,17(1): 9-12.

[17]U.S. Army Research, Development and Engineering Command. US army CERDEC dismounted solder navigation – update [EB/OL]. (2012-08-08) [2014-08-14].Http://www.docstoc.com/docs/153613635/US-ARMY-C ERDEC-Dismounted-Solder-Navigation---Update.