一种硅MEMS陀螺谐振频率与Q值的快速测量方法

卜 峰，徐大诚，赵鹤鸣

（苏州大学 微纳传感技术研究中心，苏州 215000）

基于谐振原理的硅微机电系统（Micro-Electro-Mechanical System, MEMS）陀螺具有尺寸小、重量轻、成本低等优点。谐振频率(f0)和品质因数(Q)是硅MEMS陀螺振动特性的重要参数，对驱动控制和误差机理分析具有重要作用[1]。

目前，谐振频率的测定方法主要为扫频法[2]，其原理简单，结果相对可靠，但要获得较高精度的频率需要以小间隔进行多次扫频，效率较低。为此，学者提出了一些非扫频的方法。例如，文献[3]提出了一种基于黄金分割搜索算法的谐振频率测量方法，根据几个频率点的幅值，通过寻找对称凸函数极大值的方法来求解谐振频率点。然而，在实际应用中，陀螺的幅频曲线并不一定是以谐振频率点为中心且左右完全对称的曲线。另外，对于高Q值的陀螺，其频带很窄，在不知道谐振频率下，很难取到一个有效的频率点。文献[4]利用锁相环（Phase Locked Loop, PLL）闭环控制，根据激励信号与反馈信号的相位差来寻找谐振频率点，然而在构建锁相环时也需要设定初始频率点和频率调整间隔，若初始点偏离谐振频率较远，则需要很长时间才能锁定到谐振点。文献[5]对传统PLL测量谐振频率的方法进行了改进，利用激励信号和反馈信号频率差的一个正切运算代替了PLL中的相位运算，降低了运算量，但其设定初始频率差小于200 Hz，同样存在初始信号频率点的设置问题。

对于Q值的测量，通常分为半功率带宽法(-3dB带宽法)和时间测量法。半功率带宽法[6]是根据幅频特性曲线的-3dB带宽和谐振频率来计算出Q值，精确度较低。时间测量法是根据系统的自由衰减振荡信号，在振幅衰减曲线上取2个点来计算Q值，其容易受到信号噪声和取值点选择的影响，误差也较大，而且这种方法需要陀螺产生较大幅度的余振信号，当以正弦信号为激励时，在不知道准确谐振频率下难以激励起足够大的振幅[7]。另外，通过用钝器敲击陀螺也可实现较大的初始位移，但这在物理实现上的重复性和可靠性较差，且对器件损害较大[8]。

另外，现有对于谐振频率和Q值的测量大多是分开进行的，然而陀螺系统的阻尼会在输出信号频率中有所体现[9]，因此，如果能同时对这个两个参数进行测量，则可更准确地获得陀螺系统特征。目前，还没有相关文献给出一种在完全不知道硅微陀螺谐振频率范围下，同时对谐振频率和Q值进行测量的方法，其中的难点是在不知道谐振频率下，很难找到一种激励信号使陀螺产生较大幅度的振动。

基于上述分析，提出一种同时对平板电极硅微陀螺的谐振频率和Q值进行测量的方法，其主要内容为：

1）利用平板电极结构的吸合效应，提出一种新型的激励方法，即不使用传统的正弦波激励，通过一个直流阶跃信号推动陀螺振子在其振动方向上产生固定位移，待其稳定中后切断激励信号，使其进入自由衰减振动。这样就能够在完全不知道谐振频率下使陀螺产生较大初始位移的余振。

2）将 Morlet复小波变换引入到了余振信号频率测量中，以此可解决数据点较少情况下的高精度频率测量。为了降低计算量，将Morlet复小波变换与传统FFT相结合，从而实现信号的快速频谱分析。

另外，基于时延常数法的思想，通过Hilbert变换和指数拟合来计算Q值。仿真和实验结果表明，提出的方法能够同时、快速且精确地测量谐振频率和Q值，为陀螺控制电路参数的设定提供了有力依据。

1 硅微陀螺的余振分析

振动陀螺由驱动模态和敏感模态组成，其动力学模型可由单自由度二阶系统来描述，如图1所示。单模态的动力学方程为：

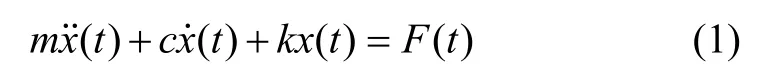
式中：m为模态质量；F(t)为激励信号；c和k分别为阻尼和刚度系数，表示为其中，ξ为模态阻尼比，为模态的自然谐振角频率。

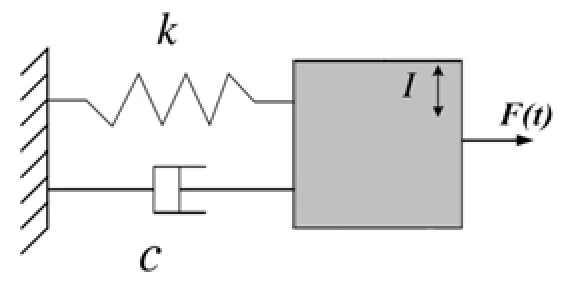
图1 陀螺单模态动力学模型Fig.1 Single-mode dynamic model of gyroscope

Q值是硅微陀螺的一个重要参数，其定义为谐振子在一个振动周期内的存储能量与消耗能量之比，即Q受到结构的气体阻尼、热弹性阻尼等多种能量损耗因子影响，因此通过结构阻尼分析来计算Q值误差较大。

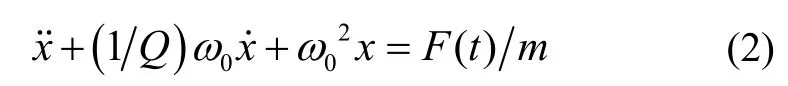
当驱动力为0，即F(t)=0时，系统呈现欠阻尼自由衰减振荡状态。通过拉普拉斯变换，可得到该模态系统的自由衰减信号为[10]：

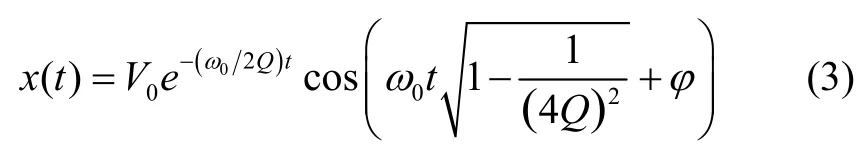
式中：φ为初始相位，V0为t=0时刻对应的信号幅度值。可以看出，自由衰减信号中包含了0ω和Q值信息，其中，余振信号的频率对于较高Q值(如Q＞100)[6]，可视为0ω=ω，即余振信号的频率就是陀螺谐振频率。为此，可利用呈现自由衰减状态的余振信号来测量谐振频率和Q值。

图2给出了一个陀螺单模态的自由衰减振荡信号的时域波形，其中，模态质量m=0.6×10-7kg，Q值Q= 5000，转动惯量I=1.1078×10-14kg·m2，刚度系数k=1.579×103N/m，初始幅度为 0.2 V，谐振频率为5000 Hz，采样频率为10 kHz。

2 方法框架

本文提出一种基于直流阶跃激励余振信号分析的硅微陀螺谐振频率和Q值测量方法，主要分为三个步骤：1）利用直流阶跃激励信号使陀螺振子产生较大初始位移的余振，同时采集余振信号，并通过带通滤波器进行消噪；2）利用FFT+Morlet复小波变换对余振信号进行高分辨率谱分析，以此获得精确的谐振频率；3）利用Hilbert变换获得余振信号的包络线，并对包络线进行最小二乘指数拟合来计算Q值。提出方法的基本框架如图3所示。

图2 陀螺自由衰减振动信号仿真Fig.2 Simulation of gyroscope free dampen vibration

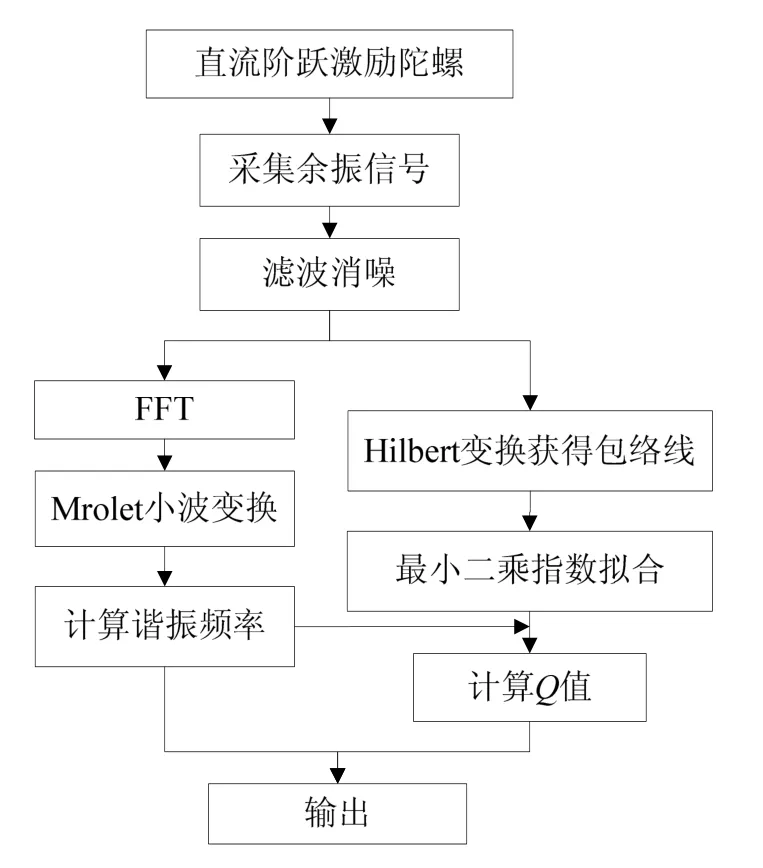
图3 提出方法的框架Fig.3 Framework of the proposed method

3 直流阶跃激励方法

3.1 问题描述

根据余振信号来测量谐振频率和Q值的方法中有个关键问题，即如何在不知道谐振频率下激励陀螺振动到足够大的振幅，以此在停止激励时获得可用的余振信号。我们知道，陀螺的幅频特性曲线类似于一个带通滤波器，Q值越高，带宽越小。在以正弦波为激励时，若给陀螺一个偏离谐振频率的激励信号（甚至偏离 1 Hz），由于陀螺的自身衰减，使其不能激励陀螺形成较大振幅的振动。为此，学者提出了一些采用PLL闭环驱动方法，利用PLL的扫频过程来使陀螺工作到谐振点。PLL扫频的效率比人工扫频效率高，但在构建 PLL时也存在初始频率和扫描间隔的设定问题。在完全不知道陀螺谐振频率范围下，设定合适的初始频率较为困难。

本文基于平板电极的吸合效应（又称 Pull-in现象），提出了一种直流阶跃激励方法。首先在单端平板电容电极上施加直流电压，使振子进入失稳状态，以此产生较大的初始位移，待其稳定后将电压变为 0，使振子进入自由衰减振荡状态。这个方法不需要考虑使陀螺工作在谐振状态来产生较大的振动幅度，且不受陀螺谐振频率点的影响，具有通用性。

3.2 吸合效应

图4描述了平板电极的力学模型，其中，两极板之间的压差为V，初始间距为d0，正对面积为A，动极板位移为x，弹簧刚度系数为k。

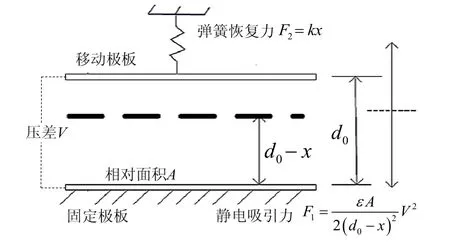
图4 平板结构电极模型Fig.4 Model of flat structure electrode

那么，板级间的静电吸引力表示为：

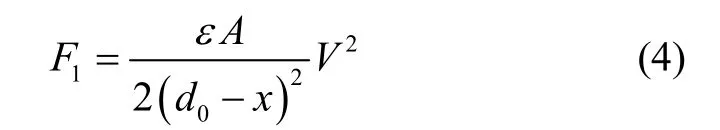
动极板所受到的弹簧恢复力表示为：

二者平衡时F1=F2，可得电压差与位移的关系，表示为：

对式(6)进行求导，可以得到极板吸合条件：

求解得：

即，当板级间距变为原来的2/3时，将发生吸合现象。此时的电压差称为吸合电压，表示为[11]：

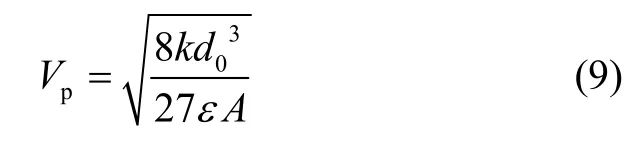
3.3 阶跃激励方法

本文利用平板电极的吸合效应来产生大幅度的初始位移。对于课题组现有的MWAV-Gyro型轮式角振动陀螺，其敏感端采用了平板电容结构。敏感端的阶跃激励（如图5所示）有两对电极，将其中一对作为检测电极，另一对作为激励电极。在其中一个激励电极上施加阶跃激励Vd，使振子产生位移。

图5 敏感端直流阶跃激励示意图Fig.5 Schematic of DC step excitation at sensitive end

不同的阶跃激励电压Vd推动振子位移的程度不同。图 6给出了当Vd=4V和Vd= 6 .5V 时，MWAVGyro型陀螺敏感端在移除激励后振子的余振波形。可以看出，激励电压幅值对余振初始幅值的影响很大，为了后续的谐振频率和Q值的有效检测，需要得到较大初始幅值的余振信号，所以需要确定合适的Vd值。

图6 不同激励电压下的余振信号波形Fig.6 Residual signal waveforms under different excitation voltages

对陀螺敏感端进行激励电压扫描，获得了余振信号初始幅度与激励电压Vd的关系曲线，如图7所示，其中基底电压可以看到，在Vd= 5 .1V时产生了阶跃变化，当时，余振信号幅度基本不变，说明此时发生了吸合效应，振子已被推到了最大位置。为此，吸合电压

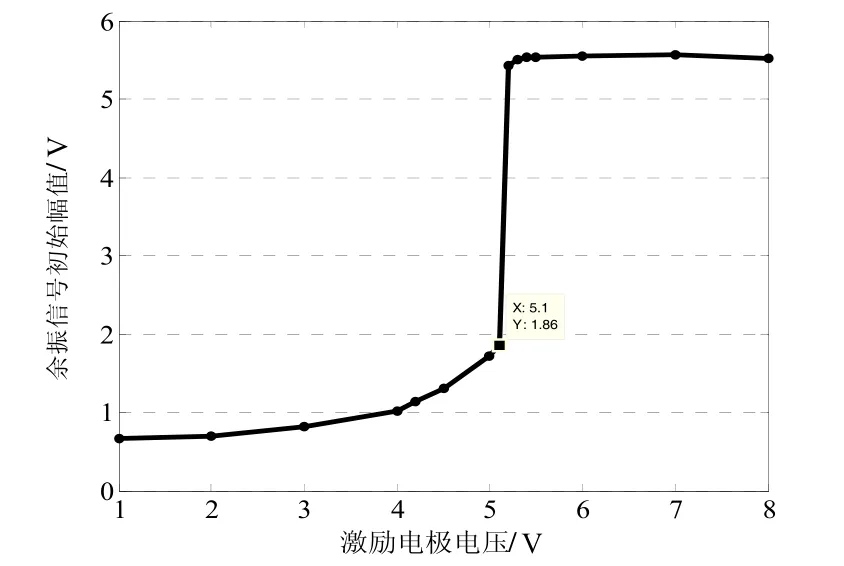
图7 余振信号初始幅度与激励电压的关系曲线Fig.7 Relationship between the initial amplitude of residual signal and the excitation voltage

从这个实验可以看出，只要施加的激励电压与基底电压差大于吸合电压Vp，即可得到较大振幅的余振信号。这里的吸合电压Vp可以通过式(9)进行计算，根据MWAV-Gyro型陀螺的结构参数，计算得到Vp的理论值为4.9 V，与实际测量值相差不大。这个偏差主要是由陀螺制造过程的工艺误差导致，但就实际操作而言，通过观察余振波形来确定激励幅值更为有效。

4 基于 FFT+Morlet复小波测量谐振频率

在通过上述方法使陀螺产生较大初始幅度的余振后，需要对余振信号进行采样并通过频谱分析来获得谐振频率0ω。传统FFT频谱分析方法的频率分辨率由采样频率和采样点数N决定，即：Δω=当采样频率为20 kHz，采样点数为1024点时，频率分辨率为19.5 Hz。而对于高Q值硅微陀螺而言，谐振频率测量精度要求较高（甚至达到0.1 Hz），传统FFT无法满足要求。另外，可通过提高采样点数来提高FFT的精度，但是，由于余振信号为渐弱信号且较高，通常无法采样到足够多的有效点数。为此，本文引入了Morlet复小波变换来对余振信号进行高精度频谱分析。

一维Morlet复小波的表达式为[12]：

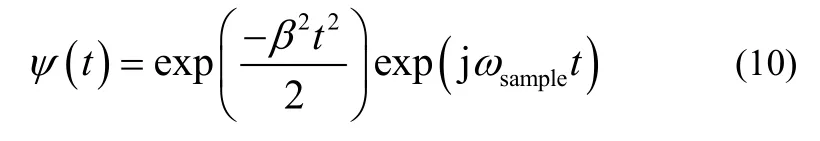
那么，对于余振信号x(t)，其Morlet复小波变换为：

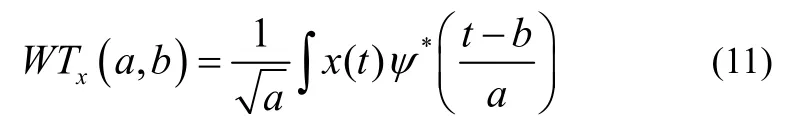
其中，a为尺度因子，b为平移因子，*表示复共轭。据 Parseval 等式，式(11)的频域表示为：

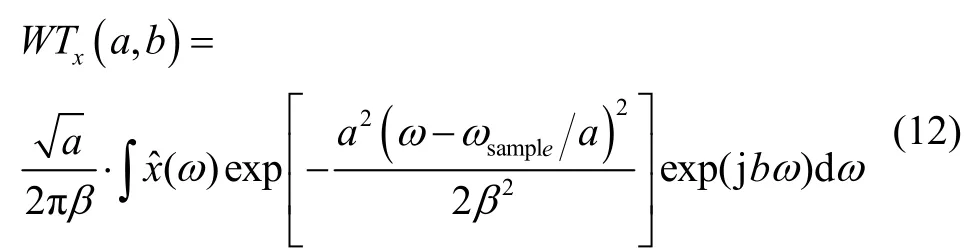
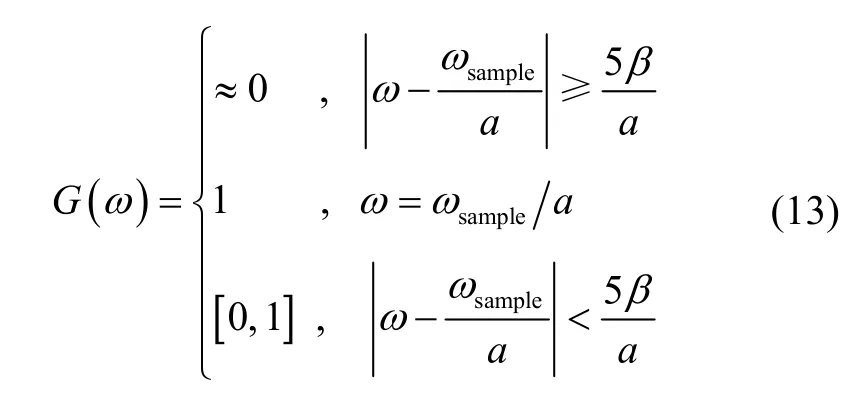
可以看出，当β取足够小时，G(ω)类似于一个冲击函数δ，可看作为一个窄带滤波器。每一个尺度对应一个窄带滤波器，其中心频率为通带为此时若取b=0，则式(12)可近似表示为：

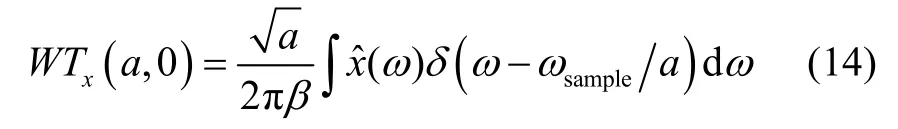
然而，若对全频谱(0 ～fsample/2)进行Morlet复小波变换，即执行a次小波变换，将会产生大量的计算。为此，本文将传统FFT与Morlet复小波变换相结合，基本步骤如下：

然后，为了确保覆盖真实频率点，在频率点fFFT附近选择出频率范围，并计算出该频率范围所对应的小波变换尺度序列。接着，对余振信号执行该尺度序列下的Morlet复小波变换。

5 基于Hilbert包络线法测量Q值

最近，文献[14]提出了一种时延常数法，根据二阶系统中自由衰减振荡信号的衰减时间系数为一常数的原理，对包络信号取对数再进行线性拟合来测量Q值。本文采用了该思想，与其不同的是，本文对于余振信号的包络，直接利用最小二乘法对包络线进行指数拟合来计算Q值，以此可简化操作步骤。

根据式(3)，陀螺余振信号的振幅曲线（即包络线）可表示为：

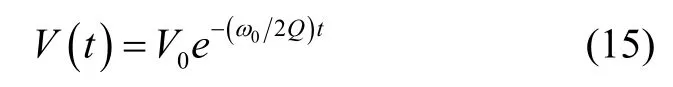
首先，对于余振信号x(t)进行Hilbert变换来获得余振信号的包络线。Hilbert变换相当于将信号通过一个冲击响应系统，在不改变信号幅度的情况下，将信号的相位改变Hilbert变换表达式为[15]：

Hilbert变换可获得余振信号x(t)的虚部～x(t)。然后将其与原始信号组成一个新的信号，对X*(t)进行取模即可获得包络线V(t)[16]，即：

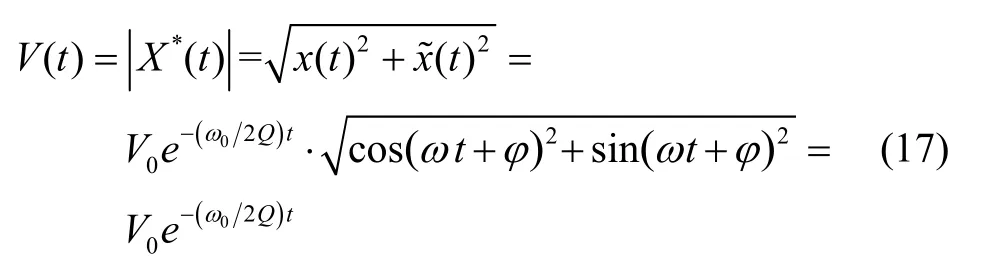
然后，采用非线性最小二乘拟合算法，对获得的包络线进行指数拟合，拟合函数为v(t) =nekt。最后，根据和已测量的ω0，即可计算出Q值。

6 仿真及实验

6.1 仿真验证

首先，通过 Matlab仿真来验证提出方法的可行性。通过Simulink构建不同谐振频率f0和Q值的单自由度二阶陀螺系统模型，再以频率为f0的正弦波激励，当其达到一定振动幅度时切断激励，使其产生自由衰减振动信号。其中取：f0∈[4901, 5101]Hz，步进值为40 Hz；Q∈[5000, 10 000]，步进值为1 000。同时，在振动信号中加入一定量的高斯噪声，性噪比为40 dB。另外，设定信号采样率fsample=62.5 kHz，信号时间长度为1 s，FFT的点数为2048点，Morlet复小波变换的尺度在不同f0和Q值下进行仿真实验，各种条件下的一次参数测量结果如表 1和表 2所示。可以看出，FFT+Morlet复小波变换的频率测量精度达到了0.1 Hz，相对误差在10-5量级上，Hilbert变换+指数拟合的Q值测量的相对误差也都达到了10-5量级。这些结果证明了提出方法的可行性。

表1 f0测量结果（Q =5000）Tab.1 f0measurement results (Q = 5000)

表2 Q值测量结果（f0=5000 Hz）Tab.2Q measurement results (f0=5000 Hz)

6.2 实验验证

以课题组现有的MWAV-Gyro型硅微轮式角振动陀螺为实验对象，测量其敏感模态的f0和Q值。其中选择了两个不同批次的陀螺，标记为陀螺1和陀螺2。阶跃激励信号由Keysight 33500B信号发生器生成，陀螺振动数据由NI M系列16位数据采集卡采集，采样率为62.5 kHz，并发送到NI LabVIEW记录软件进行记录，然后输入到Matlab进行相关计算，其中FFT点数和Morlet复小波变换的尺度参数设置与仿真中一致。

以陀螺1为例，通过阶跃激励所产生的余振波形如图9所示。可以看出，在激励电平上升后，陀螺的检测输出具有小幅度的振动，这是因为直流电压产生的静电力将振子推到平衡位置后，振子由于惯性作用在该位置附近做小幅度振动。当移除激励后，振子会产生较大幅度振动。另外，在施加直流激励时，从振动输出波形上并未看到与激励波形一样呈现一个阶跃形状，而是在0 V线上振动。这是因为陀螺敏感端的检测输出采用的是差分隔直输出形式，过滤掉了直流量，所以不会出现阶跃状。

表3 陀螺的电学参数Tab.3 Electrical parameters of the gyroscope

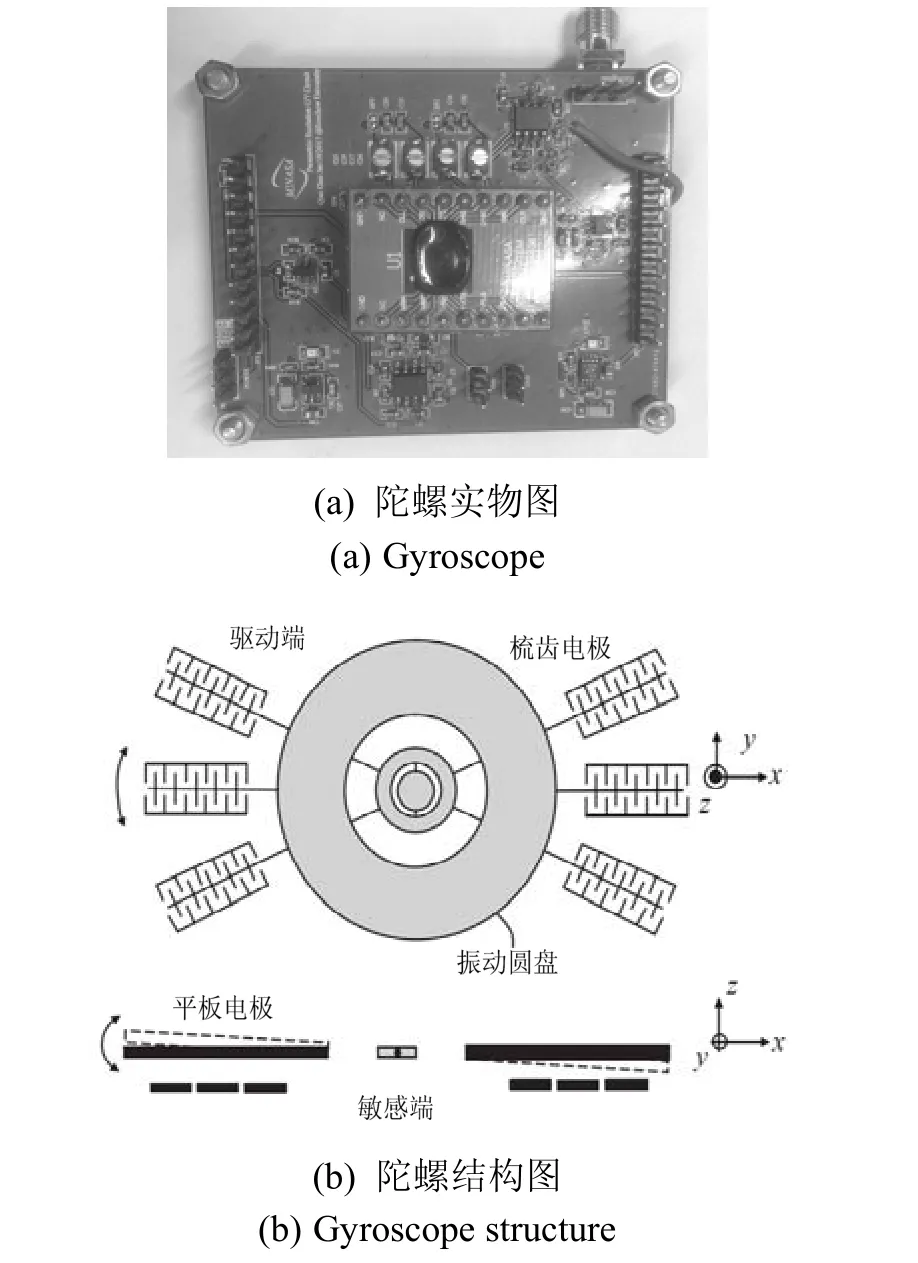
图8 实验使用的硅微轮式角振动陀螺Fig.8 The silicon micro-wheel angle gyroscope

图9 阶跃激励后陀螺1敏感模态振子余振波形Fig.9 Sensitive modal residual waveform of gyroscope 1 after step excitation

图10给出了陀螺1敏感模态一次实验采集的信号波形以及滤波消噪、频谱分析、包络线提取和指数拟合后的波形。

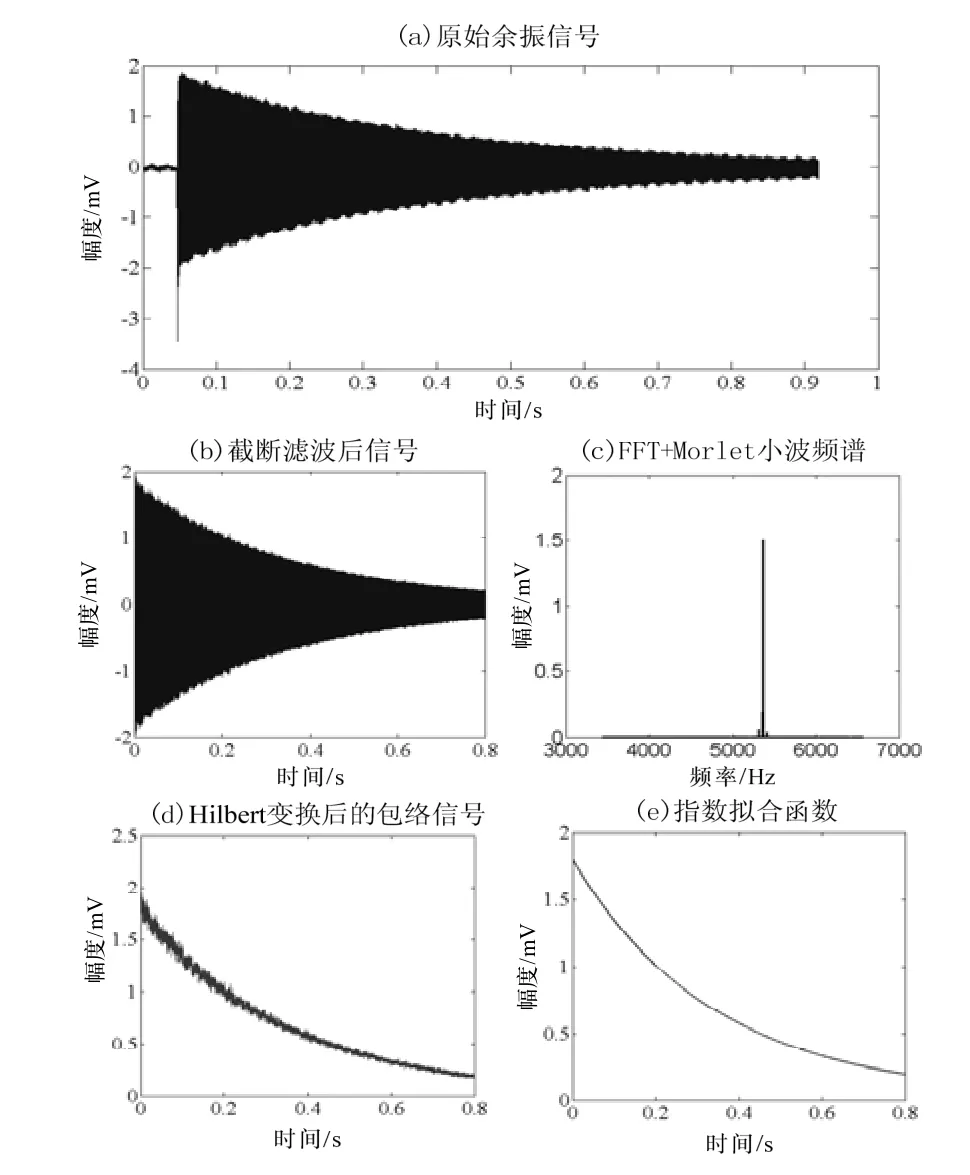
图10 实测信号及其频谱分析和包络线拟合Fig.10 Measured signal and its spectrum analysis and envelope fitting

6.3 性能比较

对于f0的测量，以扫频法作为基准，将提出方法与文献[3]提出的基于黄金分割搜索的频率测量方法进行比较。其中，扫频法是利用Keysight E5061B ENA系列网络分析仪来实现，以0.05 Hz为间隔进行扫频，谐振频率f0为幅频曲线顶点所对应的频率值。文献[3]方法是利用信号发生器输出几个频率点的正弦激励信号，基于获得的振动幅度点来估计f0。另外，为了精确比较，提出方法与文献[3]方法的频率测量精度设置为0.001 Hz。

在常温环境下，对每个陀螺的敏感模态进行多次实验。表4列出了其中3组f0的测量结果，可以看出，提出方法所获得的f0与扫频法的基本一致，相对误差在10-5量级上，这说明了提出方法的有效性。而文献[3]方法的相对误差较大，这是因为陀螺的幅频曲线不像理想情况那样完全左右对称，且该方法受到频率点选择的影响，所以不能保证有效性。另外，由于不同批次陀螺的制造环境不同，特性参数也不同，而且同一陀螺各次测试的结果也略有不同，这是因为硅微陀螺的制作材料是对温度敏感的硅材料，测试环境的变化会导致f0有略微偏移[17]。

表4 f0的测量结果比较Tab.4 Comparison on measurement results of f0Hz

对于Q值的测量，目前较为精确的方法是文献[14]描述的时延常数法，为此将该方法作为基准，将提出方法与文献[6]描述的-3 dB带宽法进行比较。-3 dB带宽法是通过f0与-3 dB带宽f-3dB的比值来计算Q值，即其中-3 dB带宽法也是通过 E5061B ENA系列网络分析仪以0.05 Hz为间隔进行扫频，基于获得的幅频曲线计算实现。时延常数法是基于扫频后获得的f0，并产生频率为f0的正弦波进行激励，以获得的余振波形来计算实现。表5列出了其中三组Q值的测量结果。

表5 Q值的测量结果比较Tab.5 Comparison on measurement results of Q

可以看出，提出方法与时延常数法的结果相近，而-3 dB带宽法对Q值测量的结果误差较大。考虑到Q值是表征陀螺振子在每个周期的能量损耗，基于振子自由衰减振荡特征的测试结果较为合理且准确。

另外，对硅微陀螺f0和Q值进行重复性测试，计算重复性测试度量：

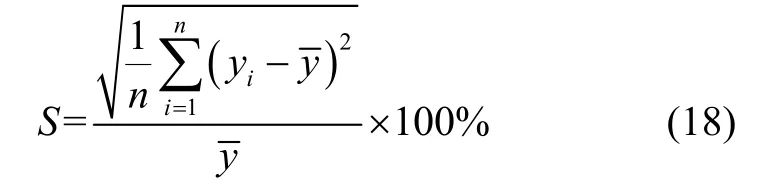
对两个陀螺的敏感模态都测试了15次，计算平均重复性测试度量值，如表6所示。结果表明，对于f0，提出方法的重复性指标与扫频法相近，且明显优于文献[3]方法，这进一步证明了提出方法的可靠性。

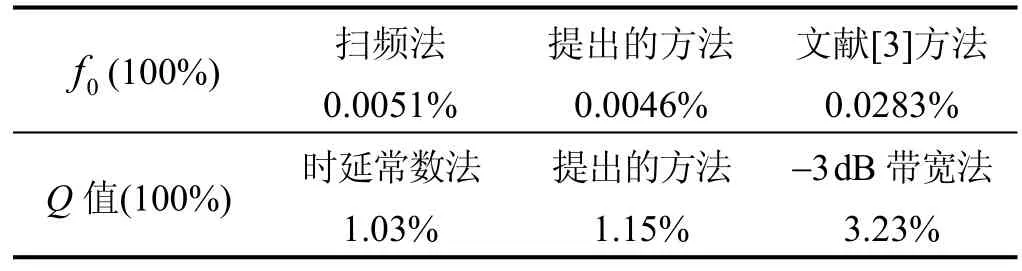
表6 重复性测试结果Tab.6 Repeatability test results

除了上述性能优势之外，所提出的方法测量一个陀螺的f0和Q值所消耗的时间不超过1 min，而扫频法则需要几十分钟甚至更长。

7 结束语

本文针对真空封装硅微陀螺的自然谐振频率和Q值的测定，提出了一种基于余振信号分析的快速测定方法。通过直流阶跃激励，在不知道谐振频率下使平板结构陀螺振子产生较大初始位移的自由衰减振动。通过结合FFT与Morlet复小波变换，实现在有限采样点下的高分辨率频谱分析。基于时延常数法的原理，通过Hilbert变换和最小二乘指数拟合来获得Q值，实现了谐振频率和Q值的同时测量。仿真和实验结果表明，提出的方法精度高、速度快且工程实现简单，具有较高的实用价值。另外，该方法也可推广到其他静电驱动类二阶谐振系统的振动特性参数测量。

参考文献（References）：

[1]Jeong C, Seok S, Lee B, et al. A study on resonant frequency and Q factor tunings for MEMS vibratory gyroscopes[J]. Journal of Micromechanics & Microengineering, 2004, 14(11): 1530-1536.

[2] 邓焱, 邢超, 张嵘, 等. 高效率的MEMS陀螺管芯动态特性测试方法[J]. 清华大学学报(自然科学版), 2014,54(6): 811-814.Deng Y, Xing C, Zhang R, et al. Rapid testing of the dynamic characteristics of MEMS gyroscope chips[J].Journal of Tsinghua University (Science and Technology Edition), 2014, 54(6): 811-814.

[3]王安成, 罗兵, 吴美平. 硅微陀螺谐振频率在线快速测定方法[J]. 中国惯性技术学报, 2011, 19(5): 607-610.Wang A C, Luo B, Wu M P. Online and quick determination of resonance frequency for silicon micromachined gyroscope[J]. Journal of Chinese Inertial Technology,2011, 19(5): 607-610.

[4]Sun X, Horowitz R, Komvopoulos K. Stability and resolution analysis of a phase-locked loop natural frequency tracking system for MEMS fatigue testing[J].Journal of Dynamic Systems Measurement & Control,2002, 124(4): 599-605.

[5]Wang A, Hu X, Luo B, et al. Two novel measurements for the drive-mode resonant frequency of a micromachined vibratory gyroscope[J]. Sensors, 2013, 13(11): 15770-15784.

[6]王安成, 胡小平, 罗兵, 等. 微机械陀螺品质因数的在线测量方法[J]. 国防科技大学学报, 2014, 36(3): 68-71.Wang A C, Hu X P, Luo B, et al. On-line measurement for the quality factor of the micro-machined gyroscope[J].Journal of National University of Defense Technology,2014, 36(3): 68-71.

[7]Wei Y, Dong Y, Huang X, et al. A stepped frequency sweeping method for nonlinearity measurement of microresonators[J]. Sensors, 2016, 16(10): 1-15.

[8]王玉朝, 滕霖, 孙香政, 等. 真空封装硅微陀螺品质因数的标定[J]. 光学精密工程, 2014, 22(10): 2708-2714.Wang Y Z, Teng L, Sun X Z, et al. Quality factor measurement of vacuum-packaged microgyroscopes[J]. Optics and Precision Engineering, 2014, 22(10): 2708-2714.

[9]董永贵, 张琦. 谐振式传感器的脉冲式双参数检测方法[J]. 清华大学学报(自然科学版), 2009, 49(5): 660-663.Dong Y G, Zhang Q. Pulsed dual-parameter measurement method for resonant sensors[J]. Journal of Tsinghua University (Science and Technology Edition), 2009, 49(5): 660-663.

[10]Yao F L, Gao S Q, Zhao J, et al. The vibration and measurement of driving mode of the two-stage decoupled micro-machined gyroscope[J]. International Journal on Smart Sensing & Intelligent Systems, 2013, 6(4): 1599-1616.

[11]樊波. 硅微角振动陀螺振动灵敏度分析及结构优化方法[D]. 苏州: 苏州大学, 2016: 34-35.Fan B. Vibration sensitivity analysis and structural optimazation of silicon micro angular vibratory gyroscope[D]. Suzhou: Soochow University, 2016: 34-35.

[12]Jiang X, Mahadevan S. Wavelet spectrum analysis approach to model validation of dynamic systems[J].Mechanical Systems & Signal Processing, 2011, 25(2):575-590.

[13]Dong H, Wu J, Zhang H, et al. Measurement of a piezoelectric transducer’s mechanical resonant frequency based on residual vibration signals[C]//IEEE International Conference on Information and Automation. 2010: 1872-1876.

[14]王玉朝, 滕霖, 孙香政, 等. 真空封装硅微陀螺品质因数的标定[J]. 光学精密工程, 2014, 22(10): 2708-2714.Wang Y Z, Teng L, Sun X Z, et al. Quality factor measurement of vacuum-packaged microgyroscopes[J].Optics and Precision Engineering, 2014, 22(10): 2708-2714.

[15]Qin Y, Liu Q. Notice of retraction on-line detection of rotor bar breaking based on band-pass filter and Hilbert envelope analysis[C]//Power Engineering and Automation Conference. IEEE, 2012: 331-334.

[16]魏玉淼, 董永贵. 从共振衰减响应中提取微机械陀螺的骨架曲线[J]. 中国惯性技术学报, 2016, 24(5):660-665.Wei Y M, Dong Y G. Extraction of micromechanical gyroscope’s backbone curves from resonance decay responses[J]. Journal of Chinese Inertial Technology,2016, 24(5): 660-665.

[17]王晓雷, 张印强, 杨成, 等. 基于数字锁相环控制的硅微陀螺仪驱动模态分析与实验[J]. 东南大学学报(自然科学版), 2013, 43(4): 747-752.Wang X L, Zhang Y Q, Yang C, et al. Analysis and experiment of drive mode of silicon micro-gyroscope based on digital phased-locked loop control[J]. Journal of Southeast University(Natural Science Edition), 2013,43(4): 747-752.