多导弹攻击时间协同的滑模制导律

花文华，张拥军，张金鹏,2，孔 石

（1. 中国空空导弹研究院，洛阳 471009；2. 航空制导武器航空科技重点实验室，洛阳 471009）

当前大多作战舰船或重要军事设施目标都安装或布置有近程防御系统用于侦查或摧毁来袭导弹，传统的比例导引制导律已越发难以胜任攻击该型目标的任务，因此具有碰撞角度[1-4]和碰撞时间[5-11]控制的先进制导律也变得越发必要。同时，面对目标的防御系统，多导弹同时攻击显然比一对一的攻击情形更容易提高导弹的生存几率和目标毁伤概率[12]。文献[5]针对攻击固定目标的情况，提出了一种次优制导律用于多枚反舰导弹的攻击时间协同，该次优制导律是比例导引律和碰撞时间误差反馈控制的组合形式。文献[6]在比例导引的基础上，设计了一种多对一的时间协同比例导引，用于舰船攻击，该制导律通过引入与多枚导弹相关的剩余飞行时间变化量，并在目标攻击过程中逐渐消除这一变化量，直到完成目标攻击。文献[7]给出了一种适用于固定目标的攻击角度和攻击时间同时可控的制导律，该制导律由减少脱靶量和碰撞角度误差的最优制导律和一个控制攻击时间的附加项构成。基于微分对策理论，考虑碰撞角度和攻击时间控制，文献[8]推导了一种适用于固定目标攻击的微分对策制导律，类似于文献[7]，该制导律首先进行碰撞角度控制最优形式的推导，在此基础上，利用对剩余飞行时间的估算将制导律扩展到同时适用于碰撞角度和攻击时间控制的形式。文献[9]提出了一种具有碰撞角度和时间控制的多项式制导律，多项式函数由具有三项可调系数的剩余下距变量构成，三项系数分别对应攻击时间、碰撞角度和脱靶量的控制。文献[5-9]的推导都基于弹目相对关系线性化近似和小角度假设，与其不同，考虑非线性弹目相对关系。文献[10]设计了一种具有碰撞角度和碰撞时间控制的滑模制导律，通过对期望视线角和视线角速度的控制间接实现对碰撞角度和碰撞时间的控制。文献[11]给出了一种攻击时间控制的滑模制导律，滑模面定义为碰撞时间误差和视线角速度的组合，以满足对碰撞时间误差和脱靶量的要求，与文献[5-10]类似，该制导律的推导同样基于目标固定的假设，但将结果扩展到了适用于非机动目标（目标运动但非机动）的情况。

本文提出一种非奇异的滑模制导律，并完成适用于机动目标的剩余飞行时间估计方法的推导和扩展，以用于多导弹的攻击时间协同。设计结果不仅适用于固定目标和非机动目标，同样适用于机动目标的攻击情形。

1 相对运动关系

导弹和目标的平面相对运动关系如图1所示，假设目标静止，导弹飞行速度基本保持不变，x轴沿初始弹目视线方向。图1中VM、aM和γM分别为导弹的飞行速度、加速度和航向角，λ为视线角，r表示弹目距离。

导弹运动方程可表示为

弹目相对运动方程如式(2)所示：

图1 平面相对运动关系Fig.1 Planar engagement geometry

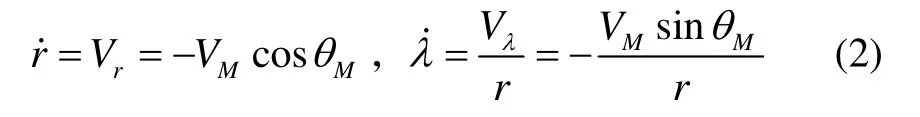
2 比例导引剩余飞行时间估计

假设导弹采用比例导引，首先完成导弹攻击固定目标的剩余飞行时间估计。

由式(1)和式(2)可以得到：

进一步结合式(2)，得：

导弹所采用的经典比例导引形式为：

式(5)中N为视线角速度和导弹航向角速度之间的比例系数。将式(2)(5)代入式(4)，并经进一步整理，可以得到：

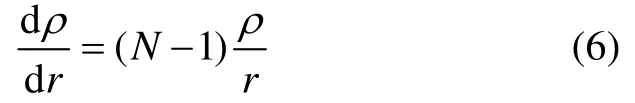
求解式(6)所示的一阶微分方程，得：

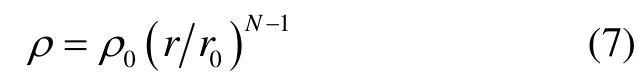
对式(2)第一式进行积分，并进行泰勒级数展开，可以得到：

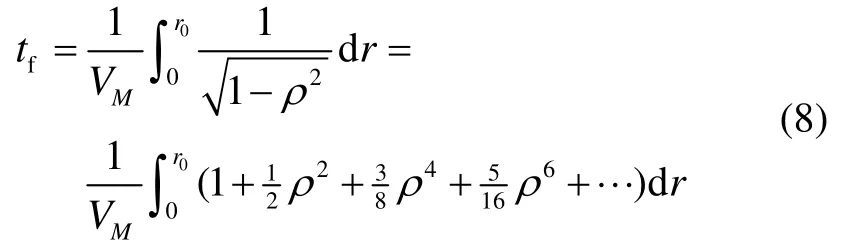
式(8)中tf为导弹的飞行时间。仅取式(8)泰勒级数展开后的前两项，并带入式(7)进行求解，可以得到：

式(10)与文献[6]的剩余飞行时间推导结果类似，但如果选取式(8)泰勒级数展开后的更多项用于导弹飞行时间的计算，结果将更为精确，因此可认为文献[6]的结果是本文的一种特殊形式。

3 攻击时间协同的滑模制导律

3.1 制导律推导

为实现多导弹攻击时间上的协同，考虑导弹飞行时间约束，定义滑模面为

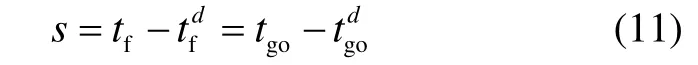
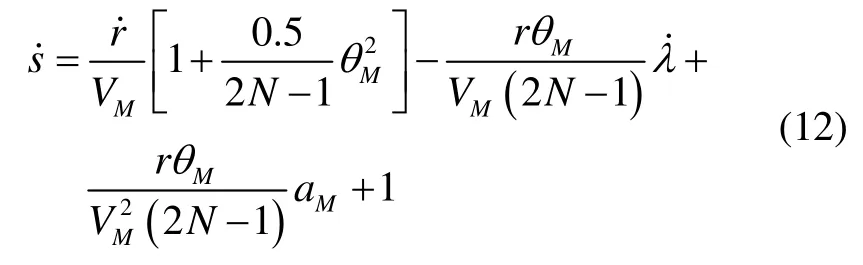
基于式(11)所定义的滑模面，所设计的制导律包括等效控制和切换控制两部分：

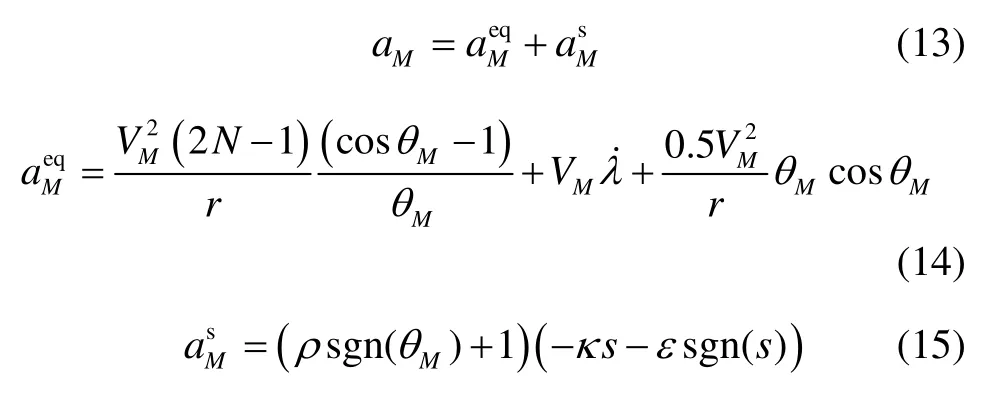
式(13)～(15)中：κ、ε、ρ为设计参数，κ,ε＞0，ρ＞ 1 ；等效控制用于消除视线角速度实现目标攻击，并保持切换控制部分用于保证滑模面s→0，满足Lyapunov稳定性条件，同时保证所推导的滑模制导律(13)是非奇异的。

将式(13)～(15)带入式(12)可以得到：

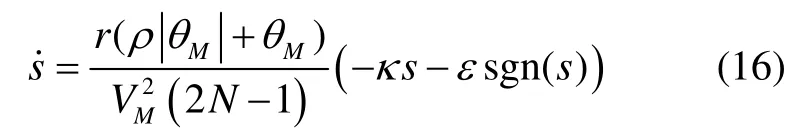
定义式(17)所示的Lyapunov函数进行稳定性的分析：

对式(17)两边求导，并代入式(16)，可以得到：

因此采用所设计的滑模制导律式(15)可以保证系统是Lyapunov稳定的。

3.2 制导律的非奇异性分析

制导律式(15)具有目标攻击和飞行时间控制两项功能。制导律是非奇异的主要是为了保证在导弹弹道收敛的情况下，即时，制导律式(13)仍是可执行的，以及仍能够满足s→0的设计要求，即导弹飞行时间总是可控的。

由式(14)，可以得到：

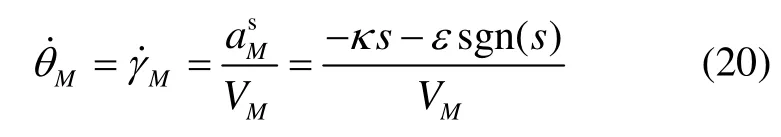
由式(20)可以发现，当s→0时，而当时，，表明即使在弹道趋于收敛的情况下，只要用于攻击时间控制的滑模面制导律式(13)就会存在相应的控制部分用于协同攻击时间，因此所设计的制导律式(13)是非奇异的。

3.3 与比例导引的等价分析

所推导的滑模制导律式(13)可转换成比例导引的等价形式。在s→0时，经进一步推导，可以得到：

图2给出了Ns随Mθ变化的曲线，从中可以发现，随着Mθ的增加，Ns逐渐增加，但变化范围较小，在Mθ可观性较差的情况下，工程上可采用比例导引替换式(14)。因此，可近似认为制导律式(15)是由比例导引和剩余飞行时间控制项两部分构成，前者用于目标攻击，后者可用于多弹攻击时间的协同。

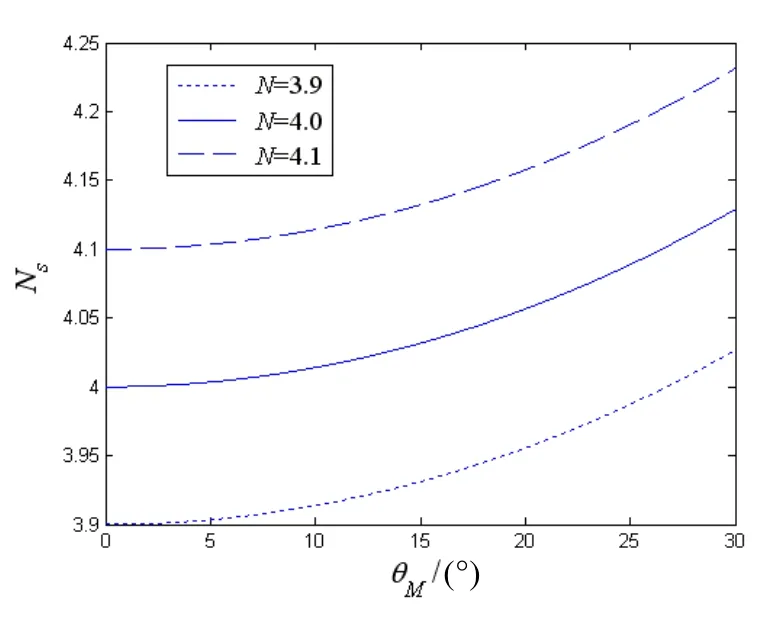
图2 Ns和Mθ之间的关系曲线Fig.2 Relationship betweenNsandMθ

4 机动目标剩余飞行时间估计

式(10)所给出的比例导引剩余飞行时间估计仅适用于固定目标，在目标运动或机动的情况下，则会产生较大的误差，从而影响控制效果，甚至带来较大的脱靶量。在式(10)的基础上，本文进一步给出一种适用于机动目标的扩展形式。基本思路为将目标速度投影到弹目视线方向上，同时考虑剩余飞行时间内由目标机动和运动所带来的目标航向和视线角的影响，以保持目标的相对静止或虚拟静止。

剩余飞行时间内目标机动所带来的航向变化和目标运动所带来的视线角变化分别为

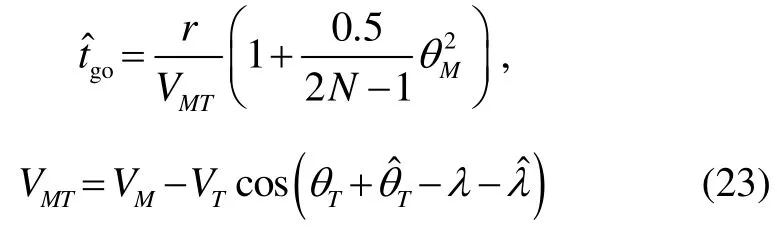
将目标当作虚拟静止目标对待进而估计剩余飞行时间是对式(10)所示形式的进一步扩展。

5 仿真结果及分析

仿真主要针对所设计的剩余飞行时间估计方法和适用于多导弹攻击时间协同的滑模制导律进行验证，验证条件主要包括多导弹攻击固定目标、非机动目标和机动目标三种情况。所设计的攻击时间协同滑模制导律适用于任意多枚导弹协同攻击的情况，具体仿真中取为三枚导弹。取导弹飞行速度160 m/s，初始航向相同γM0=60°，目标飞行速度最大机动能力1g，初始航向γM0=135°，三种情况下设定的导弹攻击时间都为仿真终止条件为脱靶量小于0.3 m，结果如图3～5所示。

图 3(a)为三枚导弹以设定的攻击时间攻击固定目标的飞行弹道。导弹1飞行弹道较为平滑，设定的飞行时间与采用经典比例导引的飞行时间tPN较为接近，而导弹2与导弹3的飞行时间则小于tPN。为满足设定的飞行时间tfd的要求，飞行弹道按照所设计的制导律式(13)进行了自适应调整，弹道曲率较大，所需的加速度也较大，如图3(b)所示。受限于最大加速度，三枚导弹在初始转弯段，为调整初始飞行航向，控制指令都出现了饱和，如图3(b)所示，但随着导弹飞行弹道的逐渐收敛，控制量逐渐减少，并趋近于零。图3(c)为三枚导弹剩余飞行时间的估计值，在弹道开始收敛后，与真实剩余飞行时间几乎重合，估计误差较小。

三枚导弹攻击非机动目标的飞行弹道、导弹加速度和剩余飞行时间估计值如图4所示。

图3 多弹协同攻击固定目标Fig.3 Cooperation attack for stationary target of multi-missiles

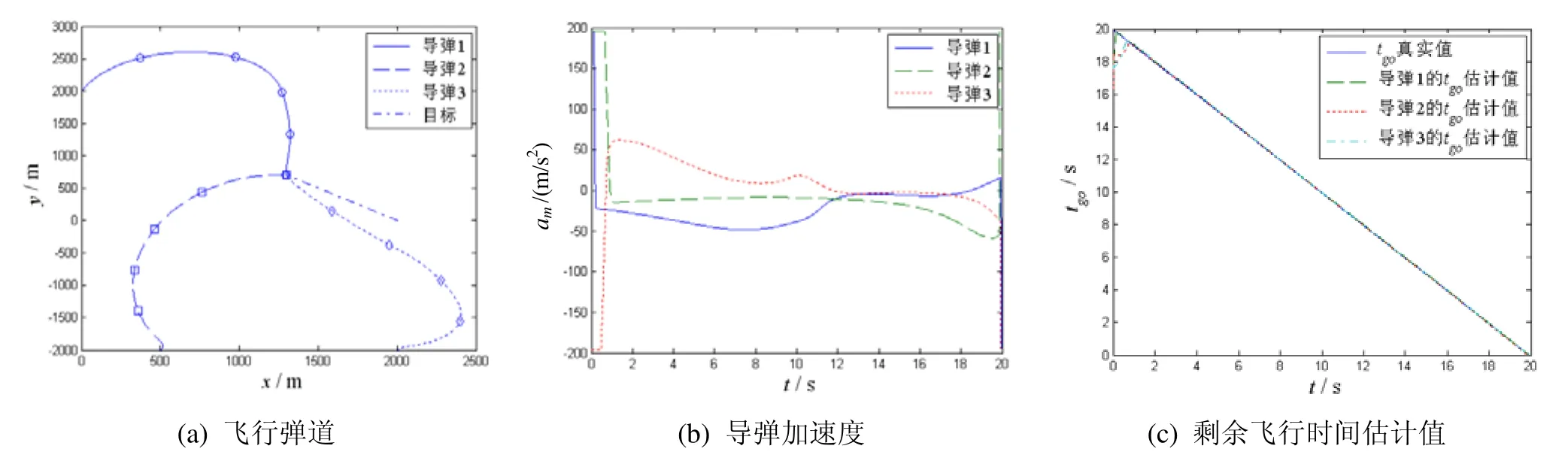
图4 多弹协同攻击运动目标Fig.4 Cooperation attack for non-maneuvering target of multi-missiles

图 5为三枚导弹攻击机动目标的飞行弹道、导弹加速度和剩余飞行时间估计值。

仿真结果与攻击固定目标的情况是类似的，表明了所给出的适用于机动目标的剩余飞行时间估计形式是正确的，且攻击时间协同滑模制导律可以实现机动目标的有效拦截，满足攻击时间协同的要求。

图5 多弹协同攻击机动目标Fig.5 Cooperation attack for maneuvering target of multi-missiles

6 结 论

1）为实现多枚导弹对目标攻击时间上的协同，设计了一种非奇异的滑模制导律，并给出了一种适用于机动目标的剩余飞行时间估计方法，据此多枚导弹能够以设定的攻击时间完成对目标的攻击；

2）通过对滑模制导律切换控制指令的合理设计，避免了所设计的滑模面的收敛和保持受到弹道收敛的影响，且总是可达的；

3）适用于机动目标的剩余飞行时间估计方法是在所推导的固定目标的剩余飞行时间估计方法基础上的扩展，采用虚拟目标的设计思路，将目标加速度和速度对弹目相对运动关系的影响投影到弹目视线方向上，从而实现目标的虚拟静止；

4）针对三枚导弹攻击固定目标、非机动目标和机动目标三种情况进行了数字仿真，结果表明了本文所设计的滑模制导律的有效性和剩余飞行时间估计方法的正确性。

参考文献（References）：

[1]李新三, 汪立新, 范小虎, 等. 带有末端角度和轨迹路径点约束的 MPSC制导律设计[J]. 中国惯性技术学报, 2016, 24(1):119-124.Li X S, Wang L X, Fan X H, et al. Guidance law of model predictive spread control with waypoints and terminal impact angle constraints[J]. Journal of Chinese Inertial Technology, 2016,24(1): 119-124.

[2]Shima T. Intercept-angle guidance[J]. Journal of Guidance, Control,and Dynamics, 2011, 34(2): 484-492.

[3]Lee C H, Kim T H, Tahk M J, et al. Polynomial guidance laws con- sidering terminal impact angle and acceleration constraints[J].IEEE Transactions on Aerospace and Electronic Systems, 2013,49(1): 74-92.

[4]宋俊红, 宋申民, 徐胜利. 带有攻击角约束的多导弹协同制导律[J]. 中国惯性技术学报, 2016, 24(4): 554-560.Song J H, Song S M, Xu S L. Cooperative guidance law for multiple missiles with impact angle constraints[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 554-560.

[5]Jeon I S, Lee J I, Tahk M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.

[6]Jeon I S, Lee J I, Tahk M J. Homing guidance law for cooperative attack of multiple missiles[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(1): 275-280.

[7]Lee J I, Jeon I S, Tahk M J. Guidance law to control impact time and angle[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 301-310.

[8]Kang S, Kim H J. Differential game missile guidance with impact angle and time constraints[C]//Proceedings of the International Federation of Automatic Control World Congress. Milano, Italy,2011: 3920-3925.

[9]Kim T H, Lee C H, Jeon I S, Tahk M J. Augmented polynomial guidance with impact time and angle constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4):2806-2817.

[10]Harl N, Balakrishnan S. Impact time and angle guidance with sliding mode control[J]. IEEE Transactions on Control Systems Technology, 2012, 20(6):1436-1449.

[11]Kumar S R, Ghose D. Sliding mode control based guidance law with impact time constraints[C]//Proceedings of American Control Conference. Washington, 2013: 5780-5785.

[12]花文华, 张拥军, 张金鹏, 等. 双导弹拦截角度协同的微分对策制导律[J]. 中国惯性技术学报, 2016, 24(6): 838-844.Hua W H, Zhang Y J, Zhang J P, et al. Differential game guidance law for double missiles with cooperative intercept angle[J].Journal of Chinese Inertial Technology, 2016, 24(6): 838-844.