高超声速飞行器助推段弹道快速计算方法

郭玮林，鲜 勇，张大巧，凌王辉

（火箭军工程大学 七系，西安 710025）

由于高超声速飞行器助推段弹道设计约束条件多，动力学过程复杂，终端入轨条件苛刻，就目前研究情况而言，实现助推段弹道优化设计本身就是一个难点问题[1-3]，若要实现助推段弹道的快速高精度计算满足高超声速飞行器机动发射要求更是一个巨大的挑战。

文献[4]针对高超声速飞行器助推段弹道设计方面进行了研究，但弹道计算速度和精度有待提高。文献[5]联合间接法和直接法可在3 min内计算生成高超声速飞行器助推段最优轨迹，但弹道计算耗时较长未达到快速计算的要求。文献[6]主要是运用牛顿迭代法实现对助推段弹道的快速计算，但牛顿法对初值敏感且易陷入局部最优。而L-M算法作为牛顿法的改进，融合了牛顿迭代局部快速收敛和梯度下降法全局迭代迅速的优点，通过引入阻尼因子，能够有效避免雅可比矩阵奇异时迭代不收敛问题[7]。

BP神经网络是一种多层前馈网络，网络结构简单实时性好，只要有足够的隐层和隐节点，就可以逼近任意的非线性映射关系[8]。基于BP神经网络建立发射点及终端入轨点状态量与弹道参数的映射关系，可以实现弹道诸元参数快速预测，为后续L-M方法数值寻优计算提供弹道参数初值。

因此本文采用基于BP神经网络和L-M方法的联合算法实现助推段弹道快速计算。首先综合考虑各项约束条件设计了助推段飞行程序和弹道优化模型；然后利用 BP神经网络预测计算诸元参数初值，并且建立了基于BP神经网络和L-M方法的联合数值计算模型；最后通过仿真实验验证了联合算法能够有效地实现助推段弹道的快速高精度计算。

1 助推段弹道设计模型

1.1 助推段飞行程序设计

以三级固体火箭作为高超声速飞行器助推段的运载器，假定地球是以角速度ω自转的椭球，且飞行器运动姿态能够达到瞬时平衡。

高超声速飞行器的助推段关机点高度相比弹道导弹较低，所以一级飞行程序采取二次攻角转弯的设计方式，即飞行器分别在跨音速前和跨音速后进行一次攻角转弯，跨音速时零攻角飞行。纵向俯仰程序设计如下：

式中：φcx表示飞行程序角；0～t1为垂直上升段；t1～t2为跨音速前攻角转弯段；t2～t3为跨音速飞行段，攻角为零；t3～t4为跨音速后攻角转弯段；t4～tk1为一二级分离前的等程序瞄准段；a1、a2、a～1、a～2为攻角设计参数；θ为弹道倾角，ωz为地球自转角速度分量。

二级和三级飞行程序采用分段线性化方法进行设计，具体形式如公式(3)，其中：为二级等程序飞行段；为二级转弯段，k1为该段的程序转弯角速率；为级间分离段；为三级转弯段，为该段的程序转弯角速率；为三级等程序飞行段，tk3为三级关机点。

1.2 助推段弹道优化模型

1）助推段约束条件

由于受到弹体结构、执行机构性能的限制，必须限制飞行器转弯角速率、过载和动压，以满足执行机构性能约束和稳定飞行的要求。为减小被敌方红外侦测系统识别的可能性，飞行器低弹道飞行时，高度须低于 90 km；同时，为顺利实现入轨飞行，助推段关机点还必须满足终端高度、速度和当地弹道倾角约束。具体约束形式如下所示：

2）优化变量的确定

所以最终高超声速飞行器助推段弹道参数确定为3个优化变量，具体如下：

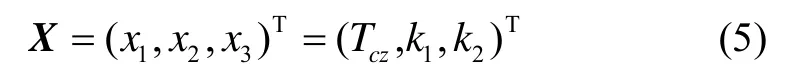
式中，Tcz为一级发动机垂直上升段工作时间。

3）目标函数

为满足高超声速飞行器终端入轨条件，采取罚函数方式将终端约束转换为目标函数，即：

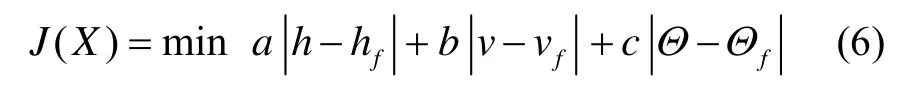
式中，a、b、c为权系数。

2 BP神经网络参数初值计算模型

以某发射区域为例进行仿真分析（假定地球为椭球，所以发射点经度改变对终端参数无影响）。为实现高超声速飞行器助推段弹道快速计算，采用 BP神经网络算法，通过训练样本，建立发射点纬度、高程、射向及关机点高度、速度、弹道倾角与助推段弹道诸元参数的函数关系式，即建立以下映射关系：

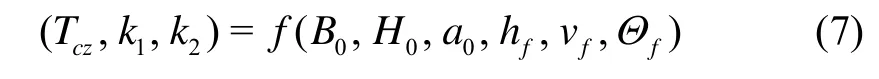
2.1 BP神经网络结构

根据BP神经网络基本原理，若确定了网络层数、各层节点数、传递函数、初始权系数和阀值、学习方法等，BP网络结构也就得以确定。

由式(7)可知，神经网络输入层节点为6个，输出层节点为3个，所以高超声速飞行器弹道模型为六输入三输出的神经网络结构。

根据Kosmogorov定理，一个具有合适参数和结构的3层BP神经网络可以完成任意的n维到m维的映射，所以可以选取3层BP神经网络结构进行仿真计算。隐层传递函数选用logsig函数，输出层传递函数选用purelin线性函数，学习方法选用L-M方法。

采用网络结构增长型方法进行仿真计算，确定隐层节点数量。通过测试误差的比较，选取隐层节点数为12个。最终确定的BP神经网络结构如图1所示。

图1 BP神经网络结构Fig.1 BP neural network structure

2.2 BP神经网络样本生成及训练

随机选取该发射区域发射点纬度、高程和射向信息，利用优化算法求解满足飞行约束和入轨终端约束的高超声速飞行器助推段弹道，从而得出5000组训练样本。由于粒子群算法具有收敛速度快、易实现的特点[9-11]，所以采用粒子群智能算法对弹道诸元参数进行优化求解，生成训练样本。

利用图1神经网络结构对样本进行训练，得到BP神经网络输入层至隐层的权值W1和阈值b1以及隐层至输出层的权值W2和阈值b2。因此可以得到发射点位置射向、关机点高度、速度、弹道倾角与弹道诸元参数的函数关系式。根据 BP神经网络结构和各层传递函数可得：

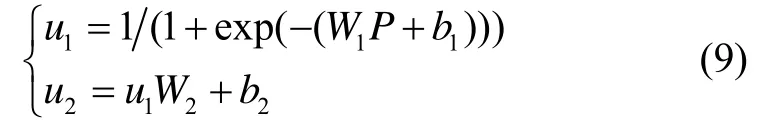
由式(8)和式(9)推导BP神经网络函数解析式的最终形式如下：

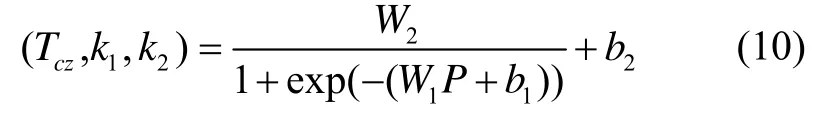
由式(10)可以快速预测计算发射区域任意发射点位相应助推段弹道诸元参数。

2.3 BP神经网络仿真计算与误差分析

训练神经网络的根本目的是确保训练好的网络模型对非训练样本具有好的泛化能力。为测试以上神经网络模型性能，再次随机选取发射区域500组测试样本，测试样本发射点位为高超声速飞行器助推段终端要求的标准高度、标准速度和标准弹道倾角为将代入BP神经网络解析式(10)即可计算得到弹道诸元参数，将该诸元参数代入高超声速飞行器标准弹道得到 BP神经网络预测的助推段终端高度、速度和弹道倾角与标准终端高度、速度和弹道倾角对比得到 BP神经网络终端高度计算偏差、速度计算偏差和弹道倾角计算偏差，如图2～4所示。基于BP神经网络方法的样本仿真统计结果如表1所示。

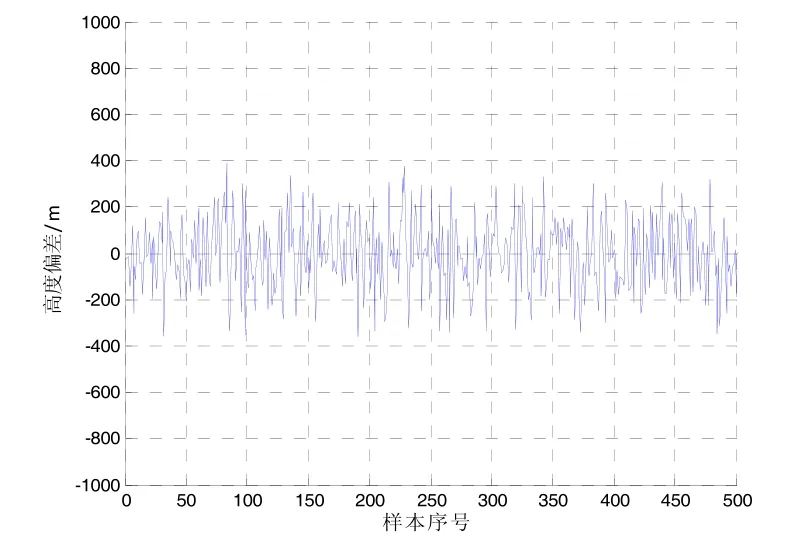
图2 BP神经网络终端高度计算偏差Fig.2 Calculated deviation of terminal height based on BP neural network

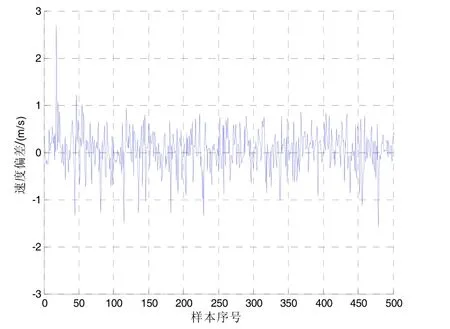
图3 BP神经网络终端速度计算偏差Fig.3 Calculated deviation of terminal velocity based on BP neural network

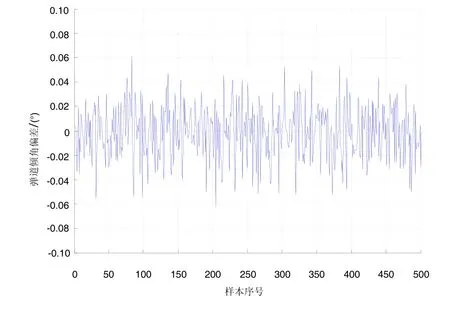
图4 BP神经网络终端弹道倾角计算偏差Fig.4 Calculated deviation of terminal inclination angle based on BP neural network

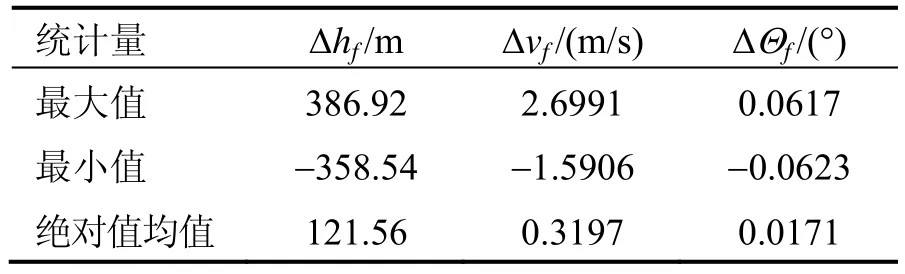
表1 基于BP神经网络的样本仿真结果Tab.1 Simulation results of samples based on BP neural network

由图2至图4和表1的仿真结果可知，基于BP神经网络求解的高超声速飞行器助推段弹道具有一定的精度，但入轨精度并不高，特别是终端高度最大入轨偏差达到386.92 m，高度平均偏差也有121.56 m，所以仅仅基于 BP神经网络计算飞行器助推段弹道精度是不够的。

BP神经网络解算的助推段弹道终端参数偏差较大，不能满足高精度入轨要求，但可以利用 BP神经网络解析式快速预测计算诸元参数，将其作为后续数值寻优计算的弹道参数初值，加快数值计算的收敛速度，以求得满足终端参数精度要求的助推段弹道。

3 BP神经网络与L-M算法联合计算模型建立

牛顿法具有收敛速度快、精度高等优点，但对初值敏感且易陷入局部最优，而L-M算法作为牛顿法的改进，通过引入阻尼因子λ，能够有效避免雅可比矩阵奇异或病态时迭代不收敛情况发生。因此可以利用BP神经网络快速预测弹道诸元参数初值，然后采用L-M算法进一步数值寻优计算，以解决机动发射条件下高超声速飞行器弹道快速计算的问题。

下面研究建立基于BP神经网络与L-M算法的联合数值寻优计算模型。

设助推段终端高度偏差Δhf、速度偏差Δvf和弹道倾角偏差ΔfΘ是诸元参数Tcz、k1、k2的三维偏差函数f(x)，即

式中，x为状态变量，将f(x)在x处进行一阶泰勒展开可得如下公式：

式中，x0为弹道诸元参数初值，Δx为迭代步长，Q为助推段终端参数偏差对诸元参数的偏导数矩阵，可采用弹道求差法计算求解。Q矩阵形式如下：

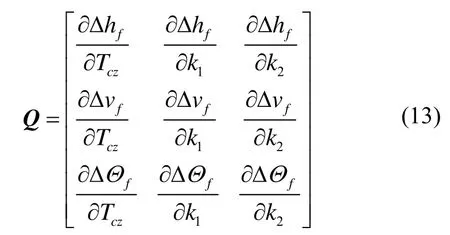
其中，弹道诸元参数初值x0的计算采用BP神经网络解析式(10)求解，即得：

助推段终端偏差函数的最小二乘模型为

将式(12)代入式(15)得到联合算法数值计算模型如下：

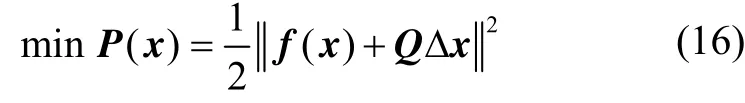
由文献[12]可知式(16)的解可表示为

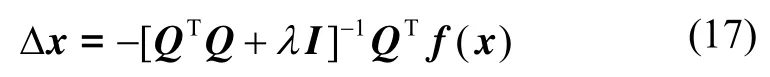
式中，λ为L-M算法的阻尼因子，λI为阻尼项。

在迭代计算过程中：当助推段终端参数偏差较大时，可以选取较大的λ，使得L-M算法具有梯度下降法下降量大、迭代迅速的特点；当助推段终端参数偏差较小时，可以选取较小的λ，使得L-M算法具有牛顿法二阶收敛的特点，从而快速收敛到最优解。

Yamashita和Fukushima在文献[13]证明了若阻尼因子时，那么在一个比非奇异性要弱的局部误差有界条件下，L-M算法将保持二次收敛。因此针对阻尼因子λ的选取，可采用如下自适应策略：

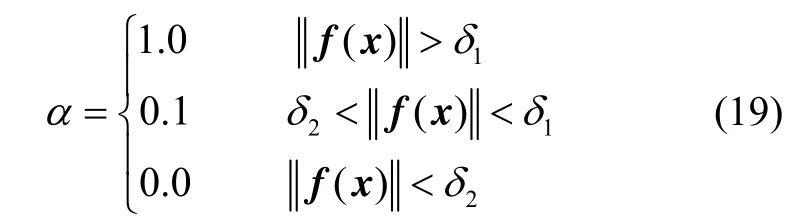
式中，1δ、2δ为终端参数偏差量范数的阀值，且0＜δ2＜δ1。

基于联合算法计算模型，根据式(17)进行多次迭代数值寻优计算，最终解得满足助推段终端入轨精度要求的弹道诸元参数。

基于BP神经网络与L-M方法的联合算法计算流程如图5所示，联合算法具体计算步骤如下：

1）将机动发射点纬度、高程和射向信息与终端入轨点高度、速度和弹道倾角参数输入到训练好的BP神经网络解析式中，计算得到弹道诸元初始值

2）再将诸元参数初值代入L-M算法数值计算模型中进行迭代寻优计算，生成新的弹道诸元参数

4）若助推段终端参数满足飞行器终端入轨精度要求或迭代达到最大次数，则退出计算，输出结果；否则，返回步骤2）。

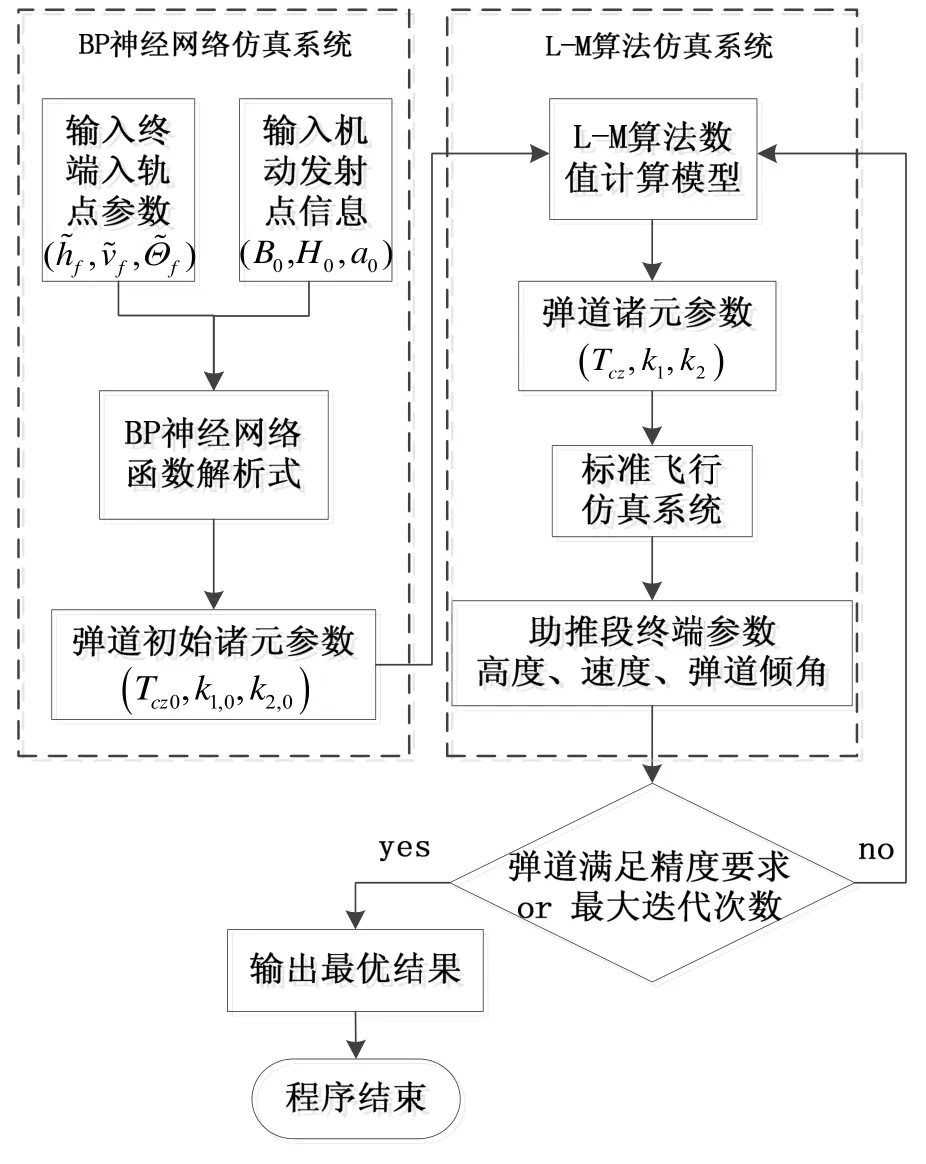
图5 联合算法计算流程图Fig.5 Flow chart of the joint algorithm

4 仿真实验结果与分析

随机选取发射区域 500组发射点位作为仿真样本，采用基于BP神经网络和L-M方法的联合算法对高超声速飞行器助推段弹道进行仿真计算得到样本助推段终端参数偏差值。基于联合算法的终端高度、速度和弹道倾角计算偏差分别如图6～8所示，助推段弹道计算耗时Ts仿真如图 9所示，基于联合算法的样本仿真统计结果如表2所示。本次仿真实验计算在普通微机上实现。

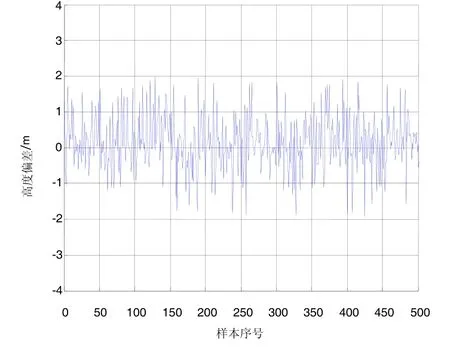
图6 联合算法终端高度计算偏差Fig.6 Calculated deviation of terminal height based on the joint algorithm

图7 联合算法终端速度计算偏差Fig.7 Calculated deviation of terminal velocity based on the joint algorithm

图8 联合算法终端弹道倾角计算偏差Fig.8 Calculated deviation of terminal inclination angle based on the joint algorithm

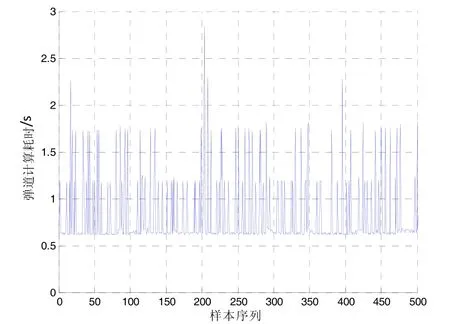
图9 弹道计算耗时仿真图Fig.9 Simulation of trajectory calculation time

由图6至图9和表2仿真结果可知，经仿真计算生成的500条助推段弹道均满足终端约束要求，并且终端高度偏差在2 m以内，终端速度偏差在0.1 m/s以内，终端弹道倾角偏差在0.01°以内，保证高超声速飞行器以较高的精度入轨。同时助推段弹道计算最大耗时为 2.84 s，平均耗时0.8211 s，弹道计算效率高、速度快。所以基于BP神经网络和L-M方法的联合算法能够较好地满足机动发射条件下高超声速飞行器助推段弹道快速高精度计算的要求。

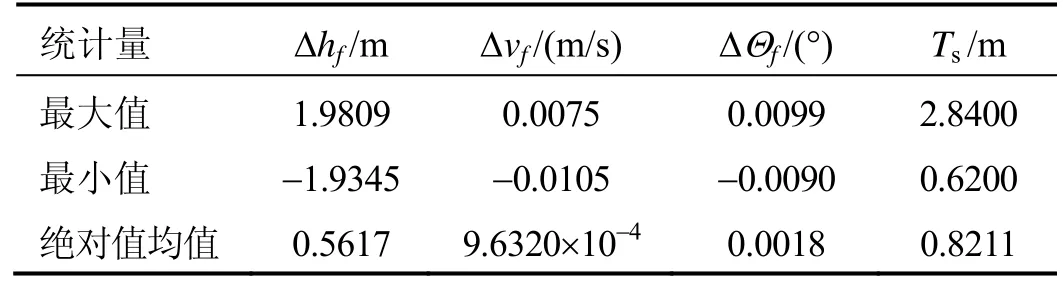
表2 基于联合算法的样本仿真结果Tab.2 Simulation results of samples based on joint algorithm

5 结 论

本文研究了机动发射条件下的高超声速飞行器助推段弹道快速计算问题。基于 BP神经网络建立了发射点及终端入轨点状态量与助推段弹道诸元参数的函数解析式，并采用 BP神经网络方法预测弹道参数初值，最终推导出基于BP神经网络和L-M算法的联合数值寻优计算模型。由仿真结果可知，采用联合算法计算得到的助推段弹道终端高度、速度和弹道倾角偏差分别在2 m、0.1 m/s和0.01°以内，弹道计算最大耗时不超过3.0 s。结果表明基于BP神经网络和L-M方法的联合算法对于机动发射高超声速飞行器助推段弹道快速高精度计算具有较强的鲁棒性和适应性。本文通过引入神经网络算法，利用BP神经网络为L-M算法数值寻优计算提供参数初值，提高了数值算法的智能化水平，较好地解决了算法计算速度的问题。

参考文献（References）：

[1]Wu G, Liu L, Wang Y, et al. Ascent trajectory optimization of hypersonic vehicle based on improved Particle Swarm algorithm[C]//IEEE Chinese Automation Congress. 2016: 115-120.

[2]Dalle D J, Torrez S M, Driscoll J F, et al. Minimum-fuel ascent of a hypersonic vehicle using surrogate optimization[J]. Journal of Aircraft, 2014, 51(6): 1973-1986.

[3]Feng L, Liu L, Wang Y. Trajectories optimization of hypersonic vehicle based on a hybrid optimization algorithm of PSO and SQP[C]//IEEE Control and Decision Conference. 2015: 4518-4522.

[4]任京涛. 助推滑翔导弹上升段多终端约束弹道设计及制导方法研究[D]. 哈尔滨: 哈尔滨工业大学硕士论文, 2013.Ren J T. Research on reconfigurable control system design of heavy launch vehicle[D]. Harbin: Harbin Institute of Technology Master Degree Dissertation,2013.

[5]崔乃刚, 傅瑜, 卢宝刚. 助推-滑翔飞行器助推段最优轨迹快速生成方法[J]. 弹道学报, 2013,25(2): 33-38.Cui N G, Fu Y, Lu B G. A fast generation method of optional trajectory of boost phase for boost-glide vehicle [J]. Journal of ballistics, 2013, 25(2): 33-38.

[6]刘开封, 陈颖, 何念念, 等. 基于正交实验与牛顿方法的滑翔导弹助推弹道设计[J]. 导弹与航天运载技术, 2014, 334(4): 50-54.Liu K F, Chen Y, He N N, et al. Boost trajectory design of boost-glide missile based on orthogonal experimental design and Newton's iterative method[J]. Missiles and Space Vehicles, 2014, 334(4): 50-54.

[7]Ma C F, Jiang L H. Some research on Levenberg-Marquardt method for the nonlinear equations[J].Applied Mathematics and Computation, 2007, 184:1032-1040.

[8]鲜勇, 李少朋, 李邦杰. 基于BP神经网络的固体导弹耗尽关机姿态调制方法的研究[J]. 兵工学报,2015, 36 (4): 668-673.Xian Y, Li S P, Li B J. An approach to attitude angle modulation of solid missiles under the condition of depleted shutdown based on BP neural network[J]. Acta Armamentarii, 2015, 36(4): 668-673.

[9]Ran M P, Wang Q. Spacecraft rendezvous trajectory optimization method based on EPSO[J]. Journal of Astronautics, 2013, 34(9): 1195-1201.

[10]Pontani M, Conway B A. Optimal finite-thrust rendezvous trajectories found via particle swarm algorithm[J]. Journal of Spacecraft and Rockets,2014, 94(1): 434-445.

[11]Zhang W, Huang X, Gao X Z, et al. Multi-objective longitudinal trajectory optimization for hypersonic reentry glide vehicle based on PSO algorithm[C]//IEEE Control Conference. 2015: 2350-2356.

[12]崔乃刚, 张亮, 韦常柱, 等. 可重复使用运载器大姿态机动自抗扰控制[J]. 中国惯性技术学报,2017, 25(3): 387-394.Cui N G, Zhang L, Wei C Z, et al. Active disturbance rejection control for reusable launch vehicle with large attitude maneuver[J]. Journal of Chinese Inertial Technology, 2017, 25(3): 387-394.

[13]Yamashita N, Fukushima M. On the rate of convergence of the Levenberg-Marquardt method[J]. Computing (Supplement 15), 2001: 239-249.