强阻尼电压源型虚拟同步发电机大扰动功角稳定性分析
孟志伟, 侯玉强,2,3,4, 方勇杰,3,4, 朱 玲,2, 杨海洋
(1. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106; 2. 国电南瑞科技股份有限公司, 江苏省南京市 211106; 3. 华北电力大学电气与电子工程学院, 北京市 102206; 4. 智能电网保护和运行控制国家重点实验室, 江苏省南京市 211106)
0 引言
随着全球范围内能源危机与环境问题的日益严重,新能源的发展得到了越来越多的重视,其在电网中的占比日益提高,并逐步进入大规模发展阶段[1]。为解决新能源机组转动惯量小,缺乏相关频率调节功能的问题,文献[2]提出了虚拟同步发电机(virtual synchronous generator,VSG)的概念。VSG将传统同步发电机的转子运动方程与电力电子的控制结合起来,通过给系统增加虚拟惯量和阻尼来改善电力系统的稳定性[3]。这一方法有效增强了电网的调节能力与抗扰动能力,但是考虑到VSG与传统同步发电机并不等价,其对电力系统的稳定性会带来更加复杂的影响。
目前,VSG稳定性的研究主要集中在小干扰稳定性方面,文献[4]给出了VSG小干扰稳定性模型,并分析了小干扰情况下,控制参数对发电机稳定性的影响;文献[5]从状态方程的角度比较了VSG控制与下垂控制技术的稳定情况; 文献[6]详细考虑了VSG滤波电感的暂态过程,指出其存在同步频率谐振现象。在大干扰稳定性研究方面,文献[7-8]给出了通过改变转动惯量,增强电力系统稳定性的方法;文献[9]指出下垂控制逆变器稳定性会受到逆变器电流限幅的影响,并给出在电流限幅影响下逆变器功角与逆变器输出电磁功率之间的关系。但是目前研究很少涉及VSG稳定性问题的定量分析,也几乎没有考虑大扰动情况下VSG阻尼系数D的影响,因此对VSG动态稳定过程的分析并不准确。
本文考虑VSG的实际运行特点,对VSG在大扰动下的功角稳定性开展研究。首先,给出VSG的一般结构,并分析其与传统同步发电机阻尼系数D及功角特性曲线之间的差异。其次,基于扩展等面积准则(EEAC)法,研究VSG-无穷大系统的稳定性问题。最后,提出了运用EEAC法判定VSG系统失稳情况的改进方法。
1 VSG基本结构
VSG有多种不同的实现方式,根据控制算法的不同,VSG分为电流控制型VSG策略和电压控制型的VSG策略[10]。对电网而言,前者可以等效为一个受控电流源,后者可以等效为一个受控电压源。从有功功率—频率控制器和无功功率—励磁控制器的角度来看,可以分为功率解耦控制的VSG和模拟同步发电机电磁方程的同步逆变器[11]。总体来说,VSG主要由能量储存单元、逆变装置及相应的VSG控制算法组成[12]。将测量的电网侧电压、频率、储能装置的充电状态信号传送到控制装置中,进而对逆变器的一侧采用VSG控制策略来使得发电系统具有类似同步发电机的控制性能,具体组成框图见附录A图A1。
VSG控制的核心环节在于有功功率—频率控制模块及无功功率—电压控制模块的实现[13]。本文采用有功功率—无功功率解耦控制的电压源型VSG的实现方案,式(1)具体给出了有功功率—频率控制和无功功率—电压控制器的相关方程。
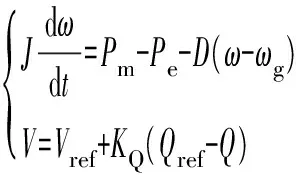
(1)
式中:J为VSG转动惯量;Pm为VSG指定机械功率;Pe为VSG的电磁功率;D为VSG阻尼系数;ω为VSG的旋转角速度;ωg为电网的旋转角速度;V为VSG的内电动势;Vref为VSG的参考电压;KQ为VSG调压系数;Qref为VSG的参考无功功率;Q为VSG的无功功率。
2 影响VSG与传统同步发电机稳定性差异的主要因素
在大扰动情况下,同步发电机的功角会发生不同程度的摆动,甚至出现功角稳定性问题。对于VSG而言,由于其模拟同步发电机的外特性,特别是模拟了同步发电机的转子运动方程,因此其具有与传统同步发电机相类似的稳定机理。为方便分析VSG在大扰动下的稳定性问题,借鉴同步发电机功角概念[14],认为VSG虚拟功角为d-q变换下d轴相对于同步旋转坐标系(x-y坐标系)实轴x轴的角位移δ,同步发电机和VSG的功角相量图详见附录A图A2。
VSG与传统同步发电机稳定性分析的不同点主要有两点:①VSG逆变器会受到电流饱和效应的影响,其电磁功率—功角曲线会发生非饱和向饱和过程的转变;②VSG阻尼系数D通常较大,应当计及其对暂态功角的影响,因此VSG的稳定性分析更加复杂。
2.1 功角特性的差异
在非饱和情况下,VSG可以等效为电压源,功角位于非饱和曲线上;而在饱和情形下,其可以等效为电流源,功角位于饱和曲线上,因此VSG功角曲线将具有式(2)所示的形式,相应的电磁功率—功角曲线图如图1所示[9]。
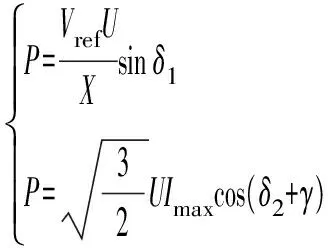
(2)
式中:P为VSG的有功功率;U为VSG的机端电压;Imax为限流电流幅值;γ为参考电流Imax与d轴之间的夹角;δ1和δ2为分别位于非饱和曲线和饱和曲线对应的虚拟功角。
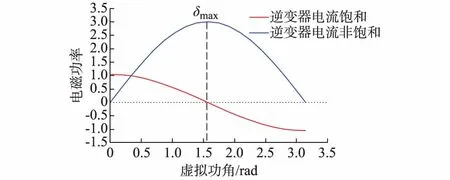
图1 VSG电磁功率-功角曲线图Fig.1 Electromagnetic power-power angle curve of VSG
2.2 阻尼系数D的差异[4]
假定VSG底层控制环响应速度足够快,在传递函数中不计其影响。而正常工作状况下,VSG运行时的虚拟功角δ′取值较小,电磁功率Pe近似满足:
(3)
式中:X为VSG的电抗。
可得到VSG近似的二阶转动方程为:

(4)
对式(4)运用拉氏变换得到其传递函数为:
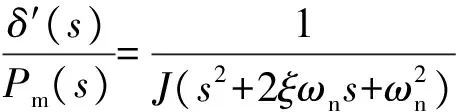
(5)
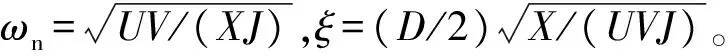
为了让二阶系统取得理想的控制性能,通常选取ξ≈0.707,在此状况下VSG阻尼系数与惯量满足关系:
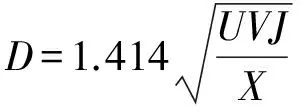
(6)
对于VSG而言,X通常很小,使得阻尼系数D取值较大,其与惯量之比的范围为10~100[15]。VSG设置强阻尼的另一个目的是改善VSG滤波电感的暂态响应过程引入的负阻尼效应[6]。但对于同步发电机而言,其阻尼系数D为发电机机械阻尼,通常仅为2%,其对暂态功角的影响可忽略不计。
3 基于EEAC法的大扰动功角稳定性分析
文献[16]表明强阻尼、低惯性的VSG在数学上可以等价为具有一阶低通滤波环节的下垂逆变器。对于此类VSG,虽然可以运用文献[9]分析下垂逆变器稳定性的方法来分析其稳定性,但是该方法一方面只能以静态情形下的等面积法则来分析下垂逆变器的功角稳定性问题,无法反映VSG系统的时变特性,尤其是无法分析系统越过不稳定平衡点后的动态行为;另一方面,该方法也无法进一步推广至多机系统,具有一定的局限性。下面采用对功角稳定性分析更为准确的EEAC法来分析大扰动下VSG的功角稳定性问题[17]。
对于VSG而言,考虑到其阻尼系数D的影响不可忽略,本文取VSG的等值参考机械功率Pm1=Pm-D(ω-ωg),此时VSG转动方程与忽略阻尼时的传统同步发电机一致,可以在P-δ相平面内分析其功角稳定性。
在P-δ相平面内考察系统运动特性可知,当Pm1-Pe与dδ符号相同时,发电机功角将加速摆动,动能增加; 相反时,动能将会减小。当动能加速面积Ainc大于动能减速面积Adec时,发电机失稳;反之,则发电机能保持稳定[17]。如图2所示,图中DSP为动态鞍点;SEP为稳定平衡点;UEP为不稳定平衡点。
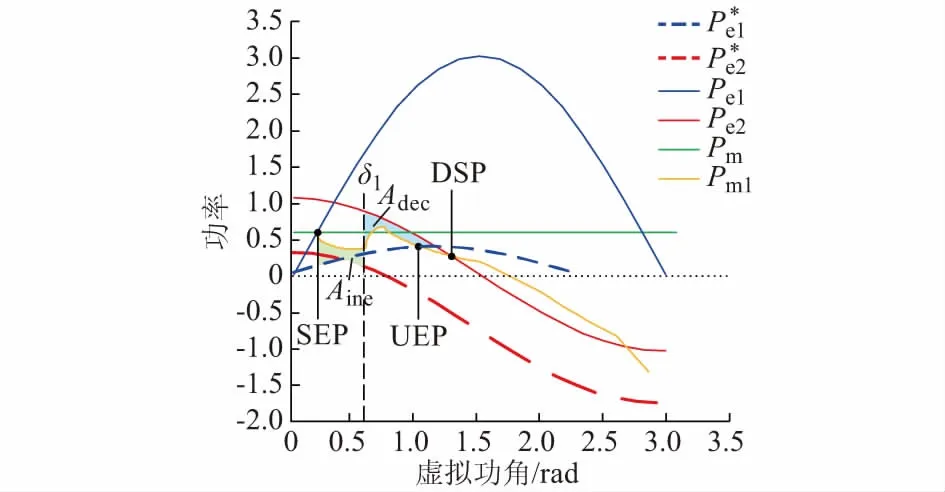
图2 VSG的P-δ相平面Fig.2 P-δ phase plane of VSG

3.1 VSG首摆稳定性判断
根据EEAC理论,DSP为在P-δ平面上,满足条件d(Pe(δ)-Pm1(δ))/dδ值为负的、时变系统的动态Pe(δ)与Pm1(δ)的交点,而系统失稳的本质是受扰轨迹经过DSP,而与UEP无直接关系。即使对于传统发电机—无穷大系统来说,当需要考虑控制器或任何时变因素时,就不能用UEP来代替DSP[17],而对于具有Pm快速受控特性的VSG则更是如此。
为了在VSG系统中验证这一结论,本文首先根据Pe2和Pm等静态特性,采用代数方法计算近似暂态稳定极限切除角,再采用基于详细模型的时域仿真方法,计算准确的极限切除角,以便将两种方法的计算结果进行比对。为了对受扰系统的首摆稳定程度进行量化,采用数字仿真和EEAC法计算轨迹稳定裕度。
3.1.1近似极限切除角的计算方法
在传统同步发电机中忽略阻尼系数D的影响,如果采用UEP代替DSP,则发电机功角首摆稳定应当满足:
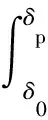
(7)
式中:δ0为发电机初始功角位置;δUEP为发电机不稳定平衡点位置;δp为故障切除时刻发电机功角位置,当δp为极限切除角δp,max时,等号成立。
由前述分析可知,VSG阻尼系数D较强,无法忽略,因此,下面将给出计及阻尼系数D情况下故障极限切除角的计算方法。对式(7)左侧运用Lagrange中值定理得到:
(8)
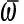
从保守角度来看,忽略式(7)右侧阻尼系数的影响,近似得到:

(9)
因此VSG极限切除角近似满足的关系为:
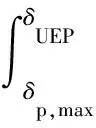
(10)
利用式(10)并采用下述迭代方法即可得到VSG的近似极限切除角δp,max:
(11)
式中:δA为给定值,一般取接近于不平衡点的值。
3.1.2基于EEAC法的轨迹稳定裕度计算
发电机功角一旦越过DSP,发电机将发生滑步,δ=δDSP首摆失稳。定义最远摆动点(FEP)为单次摆动过程中,P-δ相平面内功角δ取得极值的点[17]δ=δFEP,在这点同步发电机功角发生回摆,同时该次摆动过程中发电机功角稳定。可以得到VSG首摆轨迹稳定裕度η为:
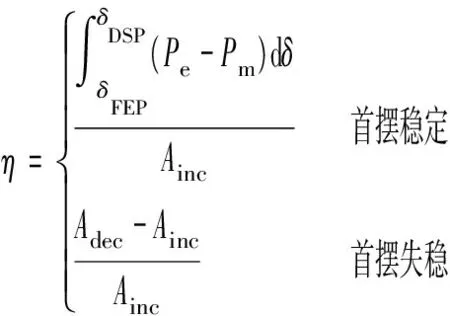
(12)
3.2 越过DSP后VSG系统稳定性判断
当虚拟功角越过DSP后,VSG发生滑步,即在首摆过程中,VSG功角失稳。但是与传统同步发电机不同,强阻尼系数D将使系统具有很强的时变特性,其稳定性将呈现出很大的不同。
事实上,VSG阻尼系数过强使得VSG参考机械功率将具有很快的响应速度及调节能力(如图2黄色实线所示),这使得VSG在越过DSP后进入多摆稳定过程。当系统的时变因素足够强时,在后续摆动中,系统仍然有可能在后一平衡点重新达到稳定,即发生滑步再同步现象[18]。
对于本文所研究的单机—无穷大系统,由于Pm1快速受控的特点,一旦前一次摆动稳定,相继的摆动必然稳定,且快速稳定于新的平衡点。但是,当前一次摆动越过DSP失稳后,在相继的摆动过程中其功角却仍可能稳定。对于这种类似于传统同步发电机中的滑步再同步现象,一方面,必须在观察时间内对受扰系统的全过程进行数字仿真;另一方面,应当尽量减少观察时间长度,以便节省计算量。为解决这一矛盾,本文采用基于EEAC法的稳定性判据,在设定的观察时间长度内,进行数字仿真,如果某一摆次稳定,则立即提前终止仿真,并判断系统稳定;如果所有摆次均越过DSP失稳,则判断系统失稳。进一步,根据受扰轨迹,计算每一摆次的动能加速面积和动能减速面积,同时结合式(12)可以得到相应摆次的系统轨迹稳定裕度,对受扰系统的稳定程度进行量化。
4 仿真验证
VSG通过变压器T,两回线L1,L2与无穷大系统相连,如附录A图A3所示。VSG采用电压控制型逆变器,并由100台光伏VSG等效而成,额定容量为50 MW,根据文献[15,19-22],设定转动惯量J=0.2(标幺值),阻尼系数D=50(标幺值),具体结构及线路图见附录B图B1, 详细参数见附录B表B1。变压器T的额定容量为100 MW,变比为0.315 kV/230 kV,漏抗为0.002(标幺值);线路L1的额定电压为230 kV,电抗为0.017 9(标幺值);线路L2的额定电压为230 kV, 电抗为0.003 44(标幺值)。逆变器在t=1 s时刻并网,并以给定功率Pm=50 MW运行。具体仿真工作在PSCAD中进行,仿真步长为500 μs。
现假定t=5 s时,线路L2发生三相短路故障;t=5.1 s时,线路L2断开,计及逆变器电流限幅作用,限幅电流Imax=170 kA。
故障切除后VSG的参考电流I随时间及虚拟功角δ的变化情况如图3和图4所示。5.1 s后故障切除,此时VSG的虚拟功角为0.624 rad,而依据前述理论,VSG此时的平衡点为0.256 rad,不平衡点为0.704 rad,功角曲线发生转变的点为0.311 rad,VSG在故障切除后将进入饱和曲线部分。在δ=π附近时,其d轴限幅效应消失,但是逆变器电流幅值仍然处于限幅状态,此时逆变器电流I与d轴的夹角γ由0逐渐变小,直到逆变器电流I与d轴负半轴重合,逆变器电流进入反向限幅状况。当虚拟功角δ=5.97 rad时,VSG逆变器电流进入非饱和状态。

图3 VSG参考电流随时间变化情况Fig.3 Reference current of VSG varied with time
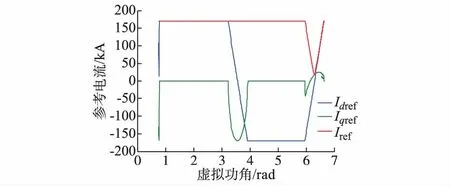
图4 VSG参考电流随虚拟功角变化情况Fig.4 Reference current of VSG varied with virtual power
VSG的输出功率Pe随时间的变化曲线如图5所示。其中红线是根据式(2)给出的逆变器电流限幅情况下VSG电磁功率的预测曲线。可见式(2)能较好地反映VSG饱和情况下的功角曲线,但由于忽略电压—电流内环的动态过程,在参考电流动态变化时,其误差较大。另一方面,图5也进一步说明了VSG功角曲线会发生非饱和向饱和之间的转变。
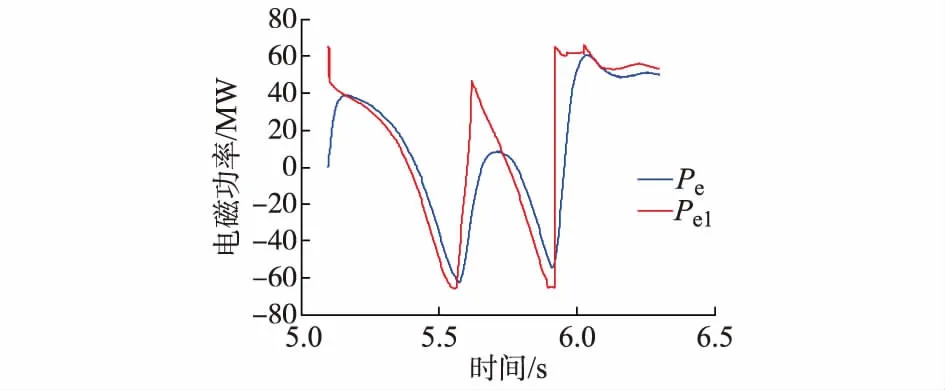
图5 VSG参考功率随时间变化情况Fig.5 Power varied with time
故障发生后,VSG故障后的各状态变量随时间的变化曲线见附录A图A4。据此,可以给出故障发生后系统的功角—角速度相平面及功角—加速度(功率差)相平面如图6所示。

图6 故障情况后VSG相平面曲线(D=50)Fig.6 Phase panel of VSG after three-phase short circuit fault (D=50)
在虚拟功角δ=δ1前,系统故障,此时参考机械功率与电磁功率之差大于0,VSG加速运动;在δ=δ1时,故障切除,此时VSG进入减速过程,并在δ=δ2处达到DSP处,此时VSG发生滑步,并进入加速摆动过程。但是由于阻尼系数D取值很大,使得系统的时变性很强,实际上在VSG虚拟功角跃过DSP后并没有彻底失步,而是进入了更为复杂的多摆过程,在[δ2,δ3]之间,VSG加速运动,而在[δ3,δ4]之间减速运动。当系统运动到后一平衡点时,由于VSG动能不足,系统将在FEP处发生回摆(此处系统频率略低于50 Hz),发生滑步—再同步现象。具体加减速面积计算结果见附录C表C1。
附录C表C1运用具体计算结果量化了强阻尼VSG跃过DSP后的运动行为,很明显,不同于传统同步发电机,具有强阻尼系数的VSG越过DSP后会发生前向多次摆动现象,但与传统同步发电机一样,在第3摆时,VSG的P-δ相平面内总减速面积大于总加速面积,致使VSG相对速度减小至负值,并进入反向摆动过程。最终VSG虚拟功角稳定在6.57 rad处,即发生了扰动后的滑步—再同步现象。
当阻尼系数D取值减小时,VSG也会发生功角失稳。依据上述方法,建立相平面如图7所示,在VSG越过DSP的后续摆次中,始终不存在减速面积大于加速面积的摆次,致使VSG频率始终大于50 Hz,其功角将不断增加而不发生回摆,最终VSG功角将失去其稳定性。
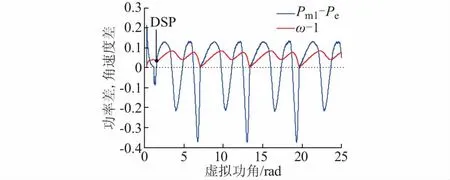
图7 故障情况后VSG相平面曲线(D=25)Fig.7 Phase panel of VSG after three-phase short circuit fault (D=25)
附录D图D1给出了不同阻尼系数情况下相对角速度和虚拟功角对比情况图,这进一步表明当阻尼系数D较强时,系统在经过DSP后,其频率仍有可能降至50 Hz以下,发生再同步现象;相反,若阻尼相对较弱,则同传统同步发电机一样,其频率将始终大于50 Hz,最终滑步失稳。
采用3.2节的判断方法,在仿真时间t=1.2 s内观察VSG功角稳定性情况,具体结果见表1。
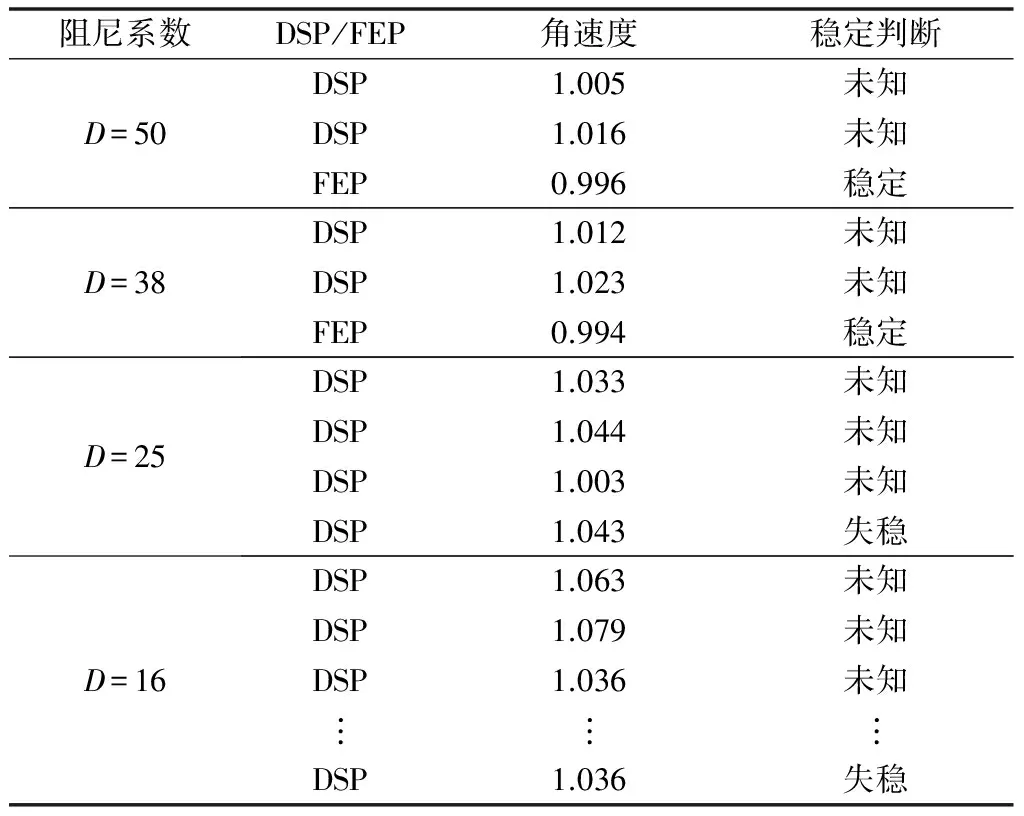
表1 不同阻尼系数下VSG功角稳定性结果Table 1 Power angle stability result of VSG in different damping coefficients
表1判断表明在D=50和D=38时,VSG功角将保持稳定;而在D=25和D=16时,VSG功角将失稳。为验证所提判断方法的合理性,图8进一步给出了多种阻尼系数下虚拟功角随时间的变化情况。由图8可见,故障情况下,D=50或D=38时,在t=6 s附近发生了再同步现象,功角稳定于6.57 rad处,当D=16或D=25时,功角不断增加以至于超过20 rad(角度为2 300°),VSG功角彻底失稳,仿真验证了所提方法的合理性。
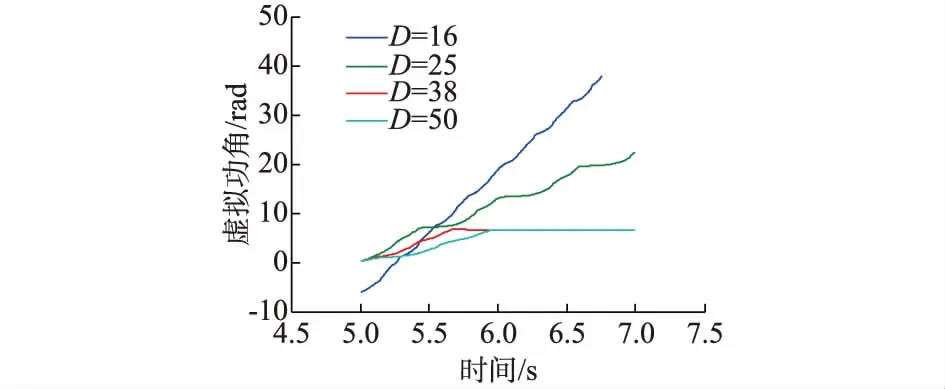
图8 不同阻尼系数下VSG虚拟功角随时间变化曲线Fig.8 Curve of VSG power angle varied with time in different damping coefficients
表2给出了按照式(11)计算出计及阻尼作用及不计阻尼系数情况下(D=0)对应首摆稳定性的故障极限切除角的近似计算结果,并与准确的实际仿真结果作对比。

表2 VSG极限切除角不同计算方法对比Table 2 Calculation results of limit clear angle in different methods
由表2可见,运用公式(12)计算极限切除角的近似值时,计及阻尼作用下的近似值更接近于准确值,但是由于在计算中忽略了线路的电磁暂态过程,忽略了VSG控制响应环节等方面的因素,导致这一计算结果与准确值之间有一定程度的偏差,结果也偏向乐观,只能作为计及首摆稳定性的极限切除角的近似评估。此外,这种近似计算没有考虑多摆稳定现象,所以无法用于实际工程。
5 结语
本文研究了强阻尼VSG-无穷大系统中在大扰动下的功角稳定性,研究表明:①在大扰动情况下,VSG阻尼系数D对其虚拟功角稳定性具有很强的影响,使得VSG系统的动态响应具有很强的时变特性,其动态过程将变得更加复杂,VSG更容易呈现多摆稳定性现象;②在单机无穷大系统中,对于VSG稳定性的判断可以基于EEAC法给出稳定性判据, 即在仿真时间内,若系统遇见FEP,则判断VSG功角在该摆次稳定; 若VSG所有摆次全部越过DSP,判断VSG失稳,进一步运用EEAC法可以给出其稳定量化裕度。
本文初步探讨了VSG功角稳定性的特性,并以此为VSG稳定性能和控制参数的进一步优化提供基础。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] 陈国平,李明节,许涛,等.关于新能源发展的技术瓶颈研究[J].中国电机工程学报,2017,37(1):20-27.
CHEN Guoping, LI Mingjie, XU Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-25.
[2] DRIESEN J, VISSCHER K, Virtual synchronous generators[C]// 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, June 20-24, 2008, Pittsburgh, USA: 1-3.
[3] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150508006.
ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150508006.
[4] 吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34(16):2591-2603.
LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.
[5] LIU Jia, MIURA Y, ISE T. Dynamic characteristics and stability comparisons between virtual synchronous generator and droop control in inverter-based distributed generators[C]// International Power Electronics Conference, May 18-21, 2014, Hiroshima, Japan: 1536-1543.
[6] 王金华.虚拟同步发电机的同步频率谐振机理和阻尼抑制[D].杭州:浙江大学,2016.
[7] ALIPOOR J, MIURA Y, ISE T. Power system stabilization using virtual synchronous generator with alternating moment of inertia[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(2): 451-458.
[8] 程冲,杨欢,曾正,等.虚拟同步发电机的转子惯量自适应控制方法[J].电力系统自动化,2015,39(19):82-89.DOI:10.7500/AEPS20141130003.
CHENG Chong, YANG Huan, ZENG Zheng, et al. Rotor inertia adaptive control method of VSG[J]. Automation of Electric Power Systems, 2015, 39(19): 82-89. DOI: 10.7500/AEPS20141130003.
[9] 黄林彬,章雷其,辛焕海,等.下垂控制逆变器的虚拟功角稳定机理分析[J].电力系统自动化,2016,40(12):117-123.DOI:10.7500/AEPS20150709007.
HUANG Linbin, ZHANG Leiqi, XIN Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123. DOI: 10.7500/AEPS20150709007.
[10] 张兴,朱德斌,徐海珍.分布式发电中的虚拟同步发电机技术[J].电源学报,2012,10(3):1-6.
ZHANG Xing, ZHU Debin, XU Haizhen. Review of virtual synchronous generator technology in distributed generation[J]. Journal of Power Supply, 2012, 10(3): 1-6.
[11] ZHONG Q, TOMAS H. Synchronverters: grid-friendly inverters that mimic synchronous generators[M]// Control of Power Inverters in Renewable Energy and Smart Grid Integration. Hoboken, USA: Wiley, 2012: 277-296.
[12] SHINTAI T, MIURA Y, ISE T. Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676.
[13] 孟建辉.分布式电源的虚拟同步发电机控制技术研究[D].北京:华北电力大学,2015.
[14] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.
[15] 李承昱,许建中,赵成勇,等.基于虚拟同步发电机控制VSC类同调等值方法[J].电工技术学报,2016,31(13):111-119.
LI Chengyu, XU Jianzhong, ZHAO Chengyong, et al. Coherency equivalence method for voltage source converter based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 111-119.
[16] D’AARCO S, SUUL A. Equivalence of virtual synchronous machines and frequency-droops for converter-based microgrids[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 394-395.
[17] 薛禹胜.运动稳定性量化理论-非自治非线性多刚体系统的稳定性分析[M].南京:江苏科学技术出版社,2002.
[18] 殷明慧,薛禹胜,邹云.受扰轨迹上动态鞍点的病态及其识别[J].电力系统自动化,2009,33(1):6-9
YIN Minghui, XUE Yusheng, ZOU Yun. Trajectory characteristic based identification of ill-conditioned DSP in EEAC[J]. Automation of Electric Power Systems, 2009, 33(1): 6-9.
[19] 吴恒,阮新波,杨东升,等.虚拟同步发电机功率环的建模与参数设计[J].中国电机工程学报,2015,35(24):6508-6518.
WU Heng, RUAN Xinbo, YANG Dongsheng, et al. Modeling of the power loop and parameter design of virtual synchronous generators[J]. Proceedings of the CSEE, 2015, 35(24): 6508-6518.
[20] CHEN Y, HESSE R, TURSCHNER D, et al. Improving the grid power quality using virtual synchronous machines[C]// International Conference on Power Engineering, Energy and Electrical Drives, May 11-13, 2011, Malaga: 1-6.
[21] 杜威,姜齐荣,陈蛟瑞.微电网电源的虚拟惯性频率控制策略[J].电力系统自动化,2011,35(23):26-31.
DU Wei, JIANG Qirong, CHEN Jiaorui. Frequency control strategy of distributed generations based on virtual inertia in a microgrid[J]. Automation of Electric Power Systems, 2011, 35(23): 26-31.
[22] 曾正,邵伟华.基于线性化模型的虚拟同步发电机惯性和阻尼辨识[J].电力系统自动化,2017,41(10):37-43.DOI:10.7500/AEPS20160729002.
ZENG Zheng, SHAO Weihua. Estimation of inertia and damping for virtual synchronous generator based on linearized model[J]. Automation of Electric Power Systems, 2017, 41(10): 37-43. DOI: 10.7500/AEPS20160729002.
孟志伟(1993—),男,硕士研究生,主要研究方向:电力系统稳定控制和新能源并网控制。
侯玉强(1983—),男,通信作者,博士研究生,高级工程师,主要研究方向:电力系统安全稳定分析与控制。E-mail: houyuqiang@sgepri.sgcc.com.cn
方勇杰(1964—),男,博士生导师,研究员级高级工程师,主要研究方向:电力系统安全稳定分析与控制。E-mail: fangyongjie@sgepri.sgcc.com.cn

