基于时间序列关联聚类的储能电池典型工况曲线提炼

杨水丽, 侯朝勇, 许守平, 赵录兴, 孙冰莹, 陈继忠

(1. 新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司), 北京市 100192; 2. 华北电力大学电气与电子工程学院, 北京市 102206)

0 引言

随着电化学储能技术在电网各领域中的应用日益广泛[1-2],建立储能电池评价体系和检测标准的紧迫性已逐渐凸显。当前主要引用相关电动汽车领域的通用检测指标或储能电池生产厂家给出的建议性测试条件,还未有针对储能电池真实工况开展评价体系和检测标准的研究[3-4],对其起重要支撑作用的储能电池典型工况适应性分析尚处于初步研究阶段。

储能典型应用工况主要有削峰填谷、调频、跟踪风电计划出力和随机出力模式等[5],通过分析储能工况适应性特性,形成适用于典型工况的通用性特征曲线,其特征参量与对应的约束条件将作为开展储能电池工况评价和检测研究的前提与依据,已受到业界关注,但尚未形成权威性的分析结果。

针对储能电池的工况特性开展的研究工作,在典型应用工况分类、工况建模以及工况测试方案等方面均取得了一定的成果。美国桑迪亚国家实验室早期将电池储能典型应用分为高倍率浅充放功率型应用与低倍率深充放能量型应用两个基本类工况[6],其研究结果适用于电池循环寿命的测试。美国西太平洋国家实验室开展了削峰填谷和调频两种工况与电池应用性能参量间的关联关系分析[3]。国际电工技术委员会在IEC标准中对储能电池的工况研究侧重于电池单体与模组[4]。文献[7]提出了一种基于实测数据统计分析的储能电池平滑风电功率波动工况曲线提取方法,该研究仅考虑了所选历史数据在统计时段内的功率—频次关系;文献[8]通过因子分析和聚类法对储能系统跟踪风电计划出力和输出功率平滑两种工况的曲线进行了提炼,以明晰各种应用中储能的工作状态及时间占比。文献[9]基于大容量储能电站在各种控制模式下的历史运行数据,提出以电池幅值分布、电流变化率及充放电转换次数等为特征值的测试工况设计方法。综观国内外研究现状,大体是基于储能工况中的运行曲线,通过独立或组合方式,重构测试工况曲线,但多为不考虑时间序列关联的特征参量聚类,缺少可动态反映储能工况数据过去及未来发展变化趋势的分析方法。

本文在未考虑时间序列而分析储能在典型工况中的功率—频次和荷电状态(SOC)—频次[10]特性关系的同时,分析考虑时间序列关联的典型工况中储能功率与SOC的周期性分布规律、交互顺序与随机变化趋势,最终提炼出具有代表性的工况曲线,为储能电池工况检测与评价提供一种更接近真实运行状态的实时动态考察手段。

1 储能电池典型工况曲线提炼分析

储能电池工况曲线获取来源于实际运行或仿真结果,通过对数据的随机与时序分布特性进行分析,辨识典型参量及外部表征。在储能电池的典型应用工况中,被重点关注的特征参量为可描述电池最大出力及出力约束的功率值,可反映电池可持续运行时长的容量值,以及用于观察运行过程中功率突变特性的功率爬坡值等。

1.1 未考虑时间序列关联的工况曲线提炼方法

储能电池典型工况提取中最基本的方法为应用概率统计法分析功率的分布特性,是应用概率的理论来研究随机现象[11],表征该事件发生的可能性数量指标,其概率值介于0和1之间。

将功率数据的分布范围等分为n段,统计各段内的数据点频次Ni(i=1,2,…,n),得到各区段内Ni个离散随机样本的频数分布函数f(x),如式(1)所示,基于函数描绘的功率—频次分布见附录A图A1(a)。将各段功率取绝对值后的频次累加,可得累计频数分布曲线,如附录A图A1(b)所示。

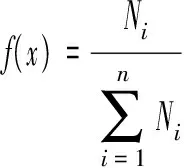
(1)

概率统计法在事件的频次比较上简单有效,可直观考察储能电池功率/SOC区间分布及对应概率(置信度),确定在满足不同置信度下所需的储能功率与容量配置值,有助于预判储能系统的实际运行状态,为工况检测与评价提供评判依据,但该方法不能动态反映工况数据过去及未来的发展变化趋势。

如附录A图A1(a)所示,基于事件频次法统计出的事件m和n在数值大小排序上处于相邻关系,但在出现时序上不一定存在前后依次关系。而典型工况曲线的提炼除了需掌握随机状态下事件的主要分布区间与频次关系,更重要的是了解它在实际运行中是如何由上一状态进入当前状态,并将怎样发展变化到下一状态,以客观真实地反映实际运行中的功率爬坡、空间特性突变及时间上的持续性等,而这些参量特性与时间序列紧密关联。

1.2 考虑时间序列关联的工况曲线提炼方法

在储能典型工况曲线提炼中,不仅需要考察特征参量发生的频次,还需分析它在时空上的演变规律和趋势特性,因而,引入一种动态数据处理的统计方法,即时间序列分析法[12],如附录B图B1所示,对按时间先后顺序排列的一组数据序列,应用数理统计方法加以处理,观测事件发展的趋势变化、周期性变化与随机性变化。由附录B图B1可知,在时间序列上,事件M发展变化到事件O经历了事件N,可反映出M发展变化到O的历程、时长及爬坡,爬坡参量影响储能实际工况中的功率特性,持续时长则影响储能实际工况中的容量特性,在附录A图A1中则不能考察出储能实际运行工况中功率与容量的实时及未来动态特性。

工况提取的目标是聚类出能表征工况特征与发展变化规律的数据群或曲线,因而需要依据某种相似性测度把需要分析的曲线集合中类似的数据对象聚成一类。聚类算法[13]中使用最为普遍的相似性测度为欧氏距离[14],能反映出在空间位置上相邻的曲线/数据点具有较高的相似性。根据全体样本点提供的信息,寻找若干符合同一分布变化规律的子数据集,并构造出一个较小的代表点集,这些代表点能够较为完整、准确地表现整个数据集的分布形状、结构特点及发展变化趋势。

数据集的分布形状、结构特点与空间距离息息相关,而事物的发展变化趋势则与时间序列强相关,因而,需要在考虑时间序列的前提下探索工况数据样本空间距离的相关性。通过分析数据样本分布与发展变化规律,确定时间序列的统计时长窗口W0,以W0为单位时间长度,将工况数据样本曲线分为n个d维曲线集,如式(2)所示。

(2)

储能系统功率P曲线集在n段d维向量间的欧氏距离描述如式(3)所示。d(Pj,Pj+m)的值越小,表征Pj和Pj+m越相似。

‖Pj-Pj+m‖2

(3)

为进一步寻找整个数据集的质心,作为将数据集聚为一类时的聚类中心[15],K类聚类问题的初始聚类中心选为(Pi1,Pi2,…,Pi(K-1),PiK),样本Pj与K个聚类中心中最近的一个之间的距离计算如式(4)所示。

bN=min{d(Pj,Pi1),…,d(Pj,PiK)}

(4)

将样本与聚类中心的最小距离定义为类内距离,选取同一聚类样本中最小的类内距离作为基点,其他样本的类内距离与该基点之差定义为类内距离缩减率[16],寻找类内距离缩减率曲线拐点,观察发展趋势的改变,以判断类内距离的截止阈值,确定第1阶段的聚类数据,如附录B图B2所示。结束第1阶段的处理后以同样的方法进入第2段阶段的辨识,以此类推。最终,确定出n个d维曲线集上具备代表性的初始聚类类数。

由于欧氏距离仅能反映聚类结构同一时刻在空间位置上相似的局部一致性特征,而无法反映聚类在基于时间序列的同一流形上相似的全局一致性。为了量度聚类数据点的全局一致性,在各个聚类样本集中定义一个流形上的线段长度[15],以量度沿着流形上的最短路径,使位于同一流形上的两点可以用较短的边相连接,而位于不同流形上的两点要用较长的边相连,放大位于不同流形上的样本间的距离。同一聚类曲线集Pi中不同时刻两点之间流形上的线段长度如式(5)所示。

L(Pji,Pj(i+t))=βd(Pji,Pj(i+t))-1

(5)

式中:d(Pji,P(j+m)i)为Pji与P(j+m)i之间的欧氏距离;β>1为伸缩因子。

根据流形上的线段长度,进一步定义一个新的距离测度,称为流形距离。将样本看作是一个加权无向图G=(V,E)的顶点V,边集合E={Wij}表示的是在每一对样本间定义的流形上的线段长度,则流形距离测度可定义为:

(6)

式中:D(Pji,Pj(i+t))为流形上两点间的距离;(Pji,Pj(i+t))表示连接样本Pi和Pj之间所有路径的集合;L(Pk,Pk+1)表示求功率两点间流形上的线段长度。

综上所述,将在初始聚类集中选取的满足流形长度量度要求的数据序列作为工况曲线提炼结果,其提炼流程如图1所示。为直观地考察工况曲线表征样本的准确性,将同一聚类曲线样本与提炼出的曲线数据间的偏差百分比及最大偏差百分比来衡量聚类后数据与实际数据的偏离程度,如式(7)所示。

(7)

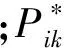
在确定的时间窗口W0内,依据在聚类类数内提炼出的功率曲线,可描述储能系统的SOC运行轨迹,如式(8)所示,可为电池的SOC控制策略制定及回归调整提供借鉴。

图1 储能电池典型工况曲线提炼流程图Fig.1 Flow chart of extraction of typical duty cycle curves of energy storage battery

(8)

式中:SSOC,k为k聚类的SOC轨迹;SSOC,e,min和SSOC,e,max为容量配置值的上、下限值。

2 算例分析

算例选取储能跟踪风电计划出力的典型应用工况,基于某100 MW风电场实际运行中的计划出力与实际出力数据[17],依据已有的风电功率预测误差标准确定储能跟踪策略生成的储能工况数据,提炼针对缩减此风电场两出力之差而所需的储能功率的特征曲线。

2.1 未考虑时间关联的工况特性分析

基于文献[17]中的风电计划出力数据与实际出力数据,计算两者的差值获得预测误差曲线,如图2(a)所示,采用概率统计分析法得出累计频数分布,如图2(b)所示。由图2(b)可知,最大功率预测误差值在25%Pe(Pe为风电场额定功率)范围内的概率约为77.8%,不满足标准要求的概率为22.15%,越过50%Pe的概率为1.6%,最大功率偏差约为76%Pe。

《风电场功率预测预报管理办法》[18]中要求风电日计划出力曲线与实际出力曲线最大误差不超过25%的风电装机容量,以平抑风电功率预测误差值至《风电场功率预测预报管理办法》中允许的范围内为控制策略,所需储能系统的功率运行曲线如附录C图C1(a)所示。依据图2(b)的频数分布特性可知,随着功率预测误差值的增大其出现概率减小,若为小概率事件而大幅提高储能功率配置值则经济性不佳。因而在配置用于跟踪风电计划出力的储能系统功率时,可考虑适当弃掉附录C图C1(a)中功率偏差值偏大而出现概率较小的情况,此类情况在提取工况特征曲线时也需对其进行处理。

图2 风电功率预测误差分布特性Fig.2 Distribution characteristics of wind power prediction error

结合文献[18]中的办法要求,得出配置不同储能系统功率值下各考核指标的完成情况如附录C图C1(b)所示。由该图中储能功率配置值与预测功率偏差合格率的对应关系可知,预测误差大小直接决定储能电池的出力,且呈正比关系,预测误差的突变决定储能电池所应具备的功率爬坡特性,其持续时长决定储能系统的容量值。因而,风电功率预测误差的校正值及校正时长为关键特征因子,直接决定储能电池SOC等相关参量的大小。

2.2 考虑时间序列关联的工况特性分析

在跟踪风电计划出力工况下确定工况数据样本合适的统计时长窗口W0,由关键特征因子即风电功率预测误差的分布与出现周期性确定。基于附录C图C1(a)中工况所需储能功率的分布曲线可知,储能系统的功率值基本在每一天的曲线中呈现出一类特性,其原因为上报调度的风电功率计划曲线以一天为周期,易出现在一天中预测功率值整体偏大或偏小的状况,且考虑到储能电池容量的持久性,选取W0=1 d的时间窗口作为分布变化周期。

以1 d为统计周期,应用聚类分析法,对n天内n个统计时段内的功率数据进行聚类划分,可基本划分为持续充电加放电、持续充电以及持续放电这3种储能运行工况模式,各模式下的特征曲线如图3所示。出现图3中3种储能运行工况分类的原因为风电预测值将在1 d或超过2 h的较长时段内整体大于/小于风电实际出力。

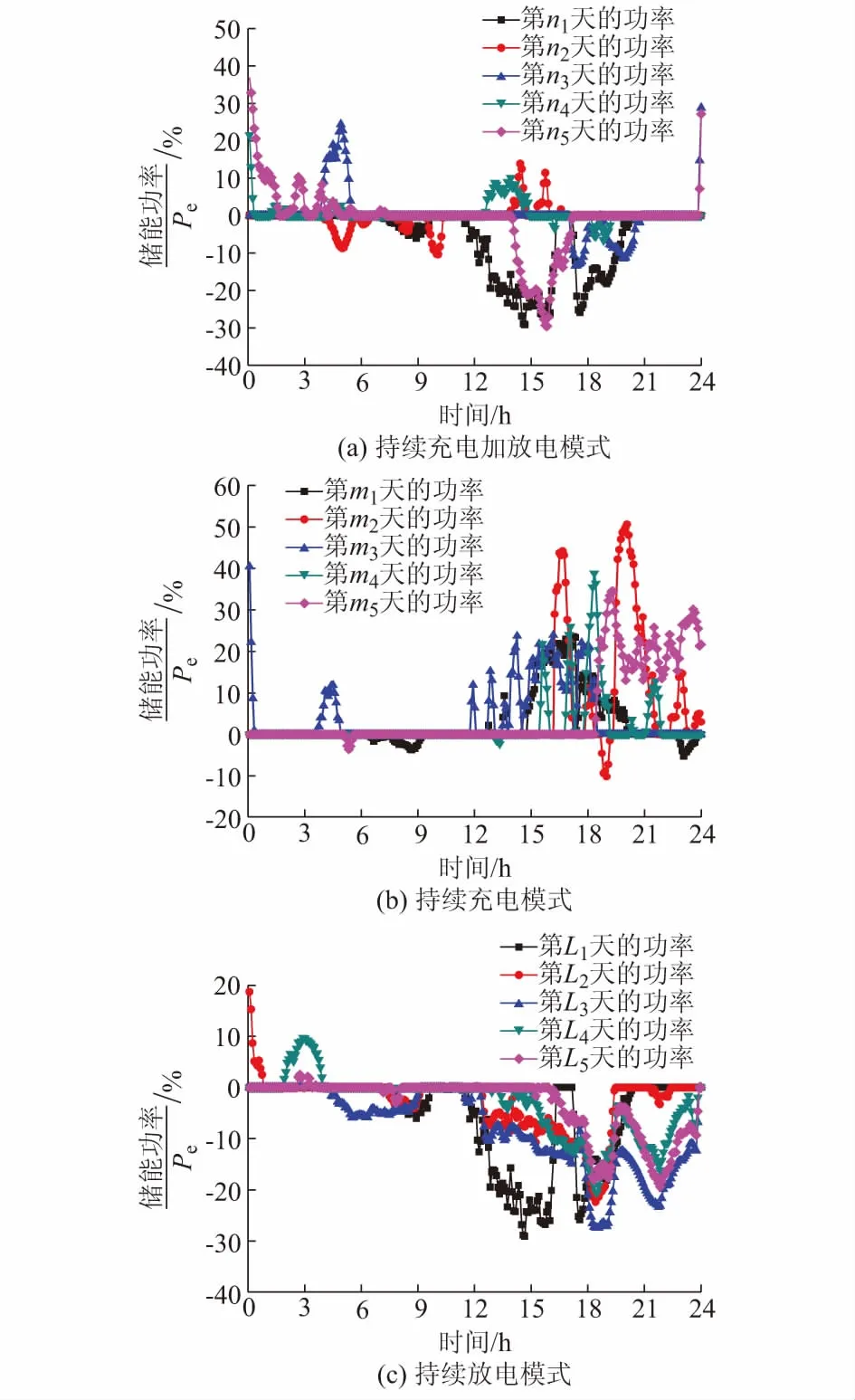
图3 储能系统运行的典型工况模式划分Fig.3 Mode division of typical duty cycle of energy storage system

针对图3中划分的3种储能典型运行工况模式,以及适当时长W0=24 h的取值,储能功率在W0时长内对时间的逐时积分可求出SOC的运行提炼曲线。计算3种储能运行工况中功率特性曲线与初始聚类样本间的类内距离,距离最小的片段即为此模式下功率轨迹相似度最大且为主要集中区的片段,根据此片段内的数据点进一步确定流形线段并计算流形距离,最终,提炼出储能电池在不同模式下的功率与SOC及爬坡率的典型曲线,如图4所示。对图3中样本数据与图4中的聚类工况数据进行偏差百分比测度,持续充电加放电、持续充电和持续放电3种模式中的最大偏差百分比分别约为12%,7%,5%,持续充电模式中出现的最大偏差百分比较大,主要原因为充电与放电交互循环中功率变化趋势难以在长时间尺度上统一。

图4 储能典型工况功率与SOC及其爬坡特 性曲线提炼图Fig.4 Extracted diagrams of power and SOC of energy storage system in typical duty cycle and their climbing characteristic curves

由图4(a)可知,在充电加放电模式中,电池储能系统的功率呈现充电与放电的阶段性状态交替特性,其最大爬坡率约为每小时7.5%Pe;由于放电状态中的深度与持续时长少于充电状态,因而,储能系统的SOC呈现缓慢正增长态势。由图4(b)可知,在持续充电模式中,储能系统的功率基本持续处于功率输入状态,其SOC处于输入累积增长态势。由图4(c)可知,在持续放电模式中,储能系统持续处于功率输出状态,其SOC处于累积增长态势。

将图4(a)、(b)、(c)中3种模式分别抽象表征为图5中的模式A、模式B和模式C,其中,模式A表征储能在一天的时长中充放电循环交互的模式,模式B表征储能的持续充电状态,模式C表征储能的持续充电状态。通过对统计时段内A,B,C这3种模式出现的概率以及交互秩序的规律分析,得出统计时段内储能系统的循环工况运行特性曲线为3B-2A-4C,如图5所示。由图5可知,3B-2A-4C的运行工况曲线表征为依次按照图4(b)中的工况曲线运行3次,图4(a)中的工况曲线运行2次,图4(c)中的曲线运行4次后,即组合成一个完整的储能运行工况特征曲线。

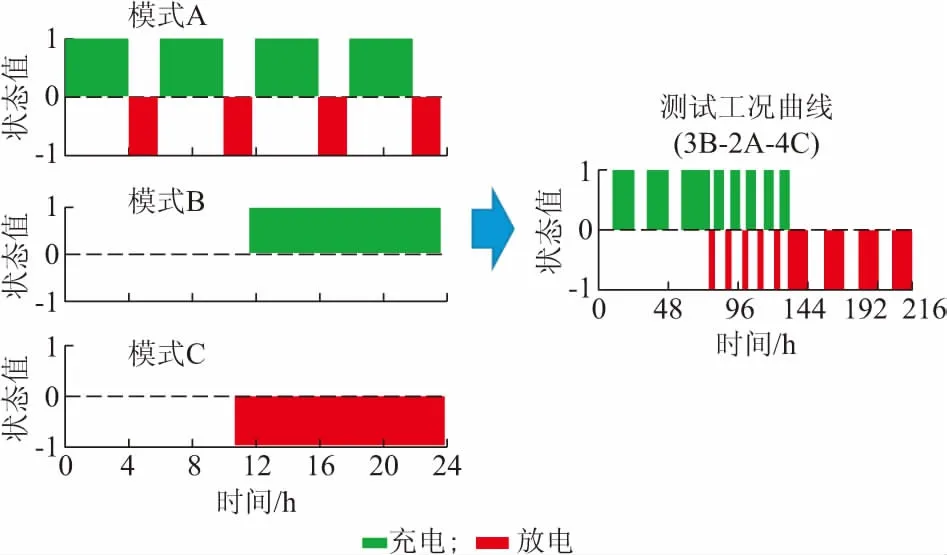
图5 储能系统运行工况特征曲线提炼过程Fig.5 Extracting process of duty cycle characteristic curve of energy storage system

2.3储能电池典型工况特征曲线对测试与运行控制的指导意义

储能电池典型工况曲线可在实验室模拟实际应用工况时,作为对试验电池进行循环充放电的参考依据,获取功率、SOC运行特性及失效表现等外在特性参数,以明确储能电池是否适应此工况下的运行需求,同时,对储能电池的测试、实际运行与控制具有指导意义,具体如下。

1)基于提炼的储能典型工况测试曲线,进行仿真或实验室工况测试,可预判此电池是否具备在此应用工况下的适用性特性,可完成对不同应用工况下适合的储能电池的筛选。

2)依据工况测试曲线中储能电池功率和SOC的分布变化规律,可有效指导电池SOC控制策略制定及回归调整。

3)为制定储能系统特性工况测试协议及工况实物测试提供参考。

4)可向储能相关消费者和使用者有效传达储能应用特性,有助于决策者在为各应用场合选择储能系统时做出更有依据的决定。

3 结语

储能电池典型应用工况特征曲线是其工况评价体系和检测标准研究的基础,本文基于储能工况运行特性,从未考虑时间序列和考虑时间序列关联两个角度对特征曲线开展了提炼分析,主要研究结论如下。

1)基于未考虑时间序列的概率统计法,可观察储能电池功率的分布变化规律及频次特性,并有助于提炼工况中的关键特征因子与参量。

2)基于时间序列关联的聚类分析法,可动态考察储能电池出力工作模式划分,各工作模式的交互顺序与出现频次及对应的SOC运行轨迹。

3)以储能电池在跟踪风电计划出力典型应用工况为例,得出风电功率预测误差的校正值及校正时长为关键特征因子,由特征因子直接决定所需储能系统相关参量,即功率、爬坡率与容量的大小;将跟踪统计时长内的储能工作模式划分为A,B,C,组合出的通用工况特征曲线为3B-2A-4C。

4)文中所提方法适用于单一应用工况曲线提炼,基于单应用工况曲线整合成适用于多应用工况下的通用性特征曲线将具有更好的工程意义。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] KOOK K S, MCKENZIE K J, LIU Y, et al. A study on applications of energy storage for the wind power operations in power system[C]// IEEE Power Engineering Society General Meeting, June 18-22, 2006, Montreal, Canada: 5p.

[2] 张文亮,丘明,来小康.储能技术在电力系统中的应用[J].电网技术,2008,32(7):1-9.

ZHANG Wenliang, QIU Ming, LAI Xiaokang. Application of energy storage technologies in power grids[J]. Power System Technology, 2008, 32(7): 1-9.

[3] FERREIRA S R, ROSE D M, SCHOENWALD D A. Protocol for uniformly measuring and expressing the performance of energy storage systems[R]. 2012.

[4] FERREIRA S, BACA W, HUND T, et al. Life cycle testing and evaluation of energy storage devices[R]. 2011.

[5] 胡娟,杨水丽,侯朝勇,等.规模化储能技术典型示范应用的现状分析与启示[J].电网技术,2015,39(4):879-885.

HU Juan, YANG Shuili, HOU Chaoyong, et al. Present condition analysis on typical demonstration application of large-scale energy storage technology and its enlightenment[J]. Power System Technology, 2015, 39(4): 879-885.

[6] EYER J, COREY G. Energy storage for the electricity grid: benefits and market potential assessment guide[R]. 2010.

[7] 仲金龙,张建文,周贤姣,等.风电场储能电池典型工况提取研究[J].电测与仪表,2015,52(9):125-128.

ZHONG Jinlong, ZHANG Jianwen, ZHOU Xianjiao, et al. Research on the typical working condition of energy storage batteries for wind farms[J]. Electrical Measurement & Instrumentation, 2015, 52(9): 125-128.

[8] 陈继忠,胡娟,武国良,等.模块化储能系统工况测试方法[J].电网技术,2016,40(11):3482-3488.

CHEN Jizhong, HU Juan, WU Guoliang, et al. Search of duty cycle test method for module ESS[J]. Power System Technology, 2016, 40(11): 3482-3488.

[9] 白恺.基于运行概率特征的电力储能系统测试工况设计方法[J].电力建设,2016,37(8):155-160.

BAI Kai. Test condition design method of power energy storage system based on operation probability characteristics[J]. Electric Power Construction, 2016, 37(8): 155-160.

[10] 全国汽车标准化技术委员会.电动汽车用电池管理系统技术条件:QC/T 897—2011[S].北京:中国计划出版社,2012.

[11] 叶瑞丽,郭志忠,刘瑞叶,等.基于风电功率预测误差分析的风电场储能容量优化方法[J].电力系统自动化,2014,38(16):28-34.DOI:10.7500/AEPS20130603009.

YE Ruili, GUO Zhizhong, LIU Ruiye, et al. A method for designing optimal energy storage system based on analysis of wind power forecast error[J]. Automation of Electric Power Systems, 2014, 38(16): 28-34. DOI: 10.7500/AEPS20130603009.

[12] 姜荣.时间序列的聚类和关联规则挖掘研究[D].大连:辽宁师范大学,2010.

[13] 白雪.聚类分析中的相似性度量及其应用研究[D].北京:北京交通大学,2012.

[14] 代倩,段善旭,蔡涛,等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报,2011,31(34):28-35.

DAI Qian, DUAN Shanxu, CAI Tao, et al. Short-term PV generation system forecasting model without irradiation based on weather type clustering[J]. Proceedings of the CSEE, 2011, 31(34): 28-35.

[15] SALVADOR S, CHAN P. Determining the number of clusters/segments in hierarchical clustering/segmentation algorithms[C]// 16th IEEE International Conference on Tools with Artificial Intelligence, November 15-17, 2004, Boca Raton, USA: 576-584.

[16] 公茂果,王爽,马萌,等.复杂分布数据的二阶段聚类算法[J].软件学报,2011,22(11):2760-2772.

GONG Maoguo, WANG Shuang, MA Meng, et al. Two-phase clustering algorithm for complex distributed data[J]. Journal of Software, 2011, 22(11): 2760-2772.

[17] 杨水丽,李建林,惠东,等.用于跟踪风电场计划出力的电池储能系统容量优化配置[J].电网技术,2014,38(6):1485-1491.

YANG Shuili, LI Jianlin, HUI Dong, et al. Optimal capacity configuration of battery energy storage system to track planned output of wind farm[J]. Power System Technology, 2014, 38(6): 1485-1491.

[18] 国家能源局.风电场功率预测预报管理暂行办法[J].太阳能,2011(14):6-7.

杨水丽(1979—),女,通信作者,硕士,工程师,主要研究方向:大规模储能技术及应用。E-mail： yangsl@epri.sgcc.cn

侯朝勇(1979—),男,博士,高级工程师,主要研究方向:大规模储能技术及应用。E-mail: houchaoyong@epri.sgcc.cn

许守平(1978—),男,博士,工程师,主要研究方向:大规模储能技术及应用。E-mail: shishouping@epri.sgcc.cn