基于自适应虚拟惯性的微电网动态频率稳定控制策略
刘 尧, 陈建福, 侯小超, 裴星宇, 李建标, 粟 梅
(1. 广东电网有限责任公司珠海供电局, 广东省珠海市 519000; 2. 中南大学信息科学与工程学院, 湖南省长沙市 410000)
0 引言
分布式发电具有环境友好、范围广、高灵活性等明显的优势,近年来越来越受到社会各界的广泛关注[1]。而微电网整合分布式发电的资源,通过电力电子变换器将发电侧和用户负荷连起来,作为整体可控的独立电网[2]。相对于传统的大电网而言,微电网具有一些固有特征:快速响应能力、缺乏惯性缓冲和较低的过载能力。所以,储能是保证微电网电力负荷供电质量的关键,特别是针对随机、高波动性的负荷,储能能起到平缓功率、提升电能质量和提高系统稳定性的作用[3-4]。
为了提高微电网系统的频率动态稳定性,利用储能的思路受到研究者的关注[5],本质上短期的储能供应为微电网提供了虚拟惯性[6-7],另一种思路是基于虚拟同步发电机(virtual synchronous generator,VSG)的控制技术[8-11]。文献[8]提出并网同步逆变器用于模仿发电机的行为。文献[9]提出一种新型的频率控制模式来调节直流电压,从而提供系统阻尼和惯性环节。文献[10]阐述了旋转式同步发电机和静止式同步发电机的固有区别,对比分析了两者的稳定性。文献[11]也在分布式电源(DG)逆变器中引入同步发电机的思想,并分析了存在中间直流扰动时的系统稳定性。尽管上述文献[8-11]建立了逆变器和同步发电机的等效关系,但是不能提高系统频率的动态稳定性。
另一方面,微电网传统下垂控制模拟电力系统发电机的行为,通过DG的频率和电压调整自身输出功率[12],然而该方法不能模拟同步发电机的暂态性能。文献[13]利用有功—频率下垂外环作为虚拟惯性部分,模仿同步发电机的行为在高压直流输电系统中应用。文献[14]建立了基于虚拟同步发电机和下垂控制的微电网小信号模型,对比分析了两者的暂态响应,并利用状态空间模型分析有功振荡问题,得出虚拟同步发电机控制不仅具有下垂控制的稳态效果,还能提供额外的虚拟惯性部分,提高系统的动态稳定性。
为此,一些研究者对下垂控制进行改造以提高系统的暂态响应能力[15-18]。文献[15]修改下垂增益,构造增益与频率微分的函数,用于减少频率的偏差变化,但没有利用频率变化符号的优势。文献[16]在文献[15]的基础上,利用频率的变化虚拟惯性部分,然而该方法仅有两个值可等效于开关控制。文献[19]根据同步发电机功角特性提出一种转动惯量自适应控制策略,实现频率动态控制。综上所述,大部分文献对传统下垂控制和虚拟同步发电机控制进行改进,但难以解决系统频率动态稳定性问题。为了克服上述固定虚拟惯量[8-11]、变惯量[15]、交替惯量[16]的缺点,本文提出一种基于自适应虚拟惯性的同步发电机控制策略,从仿真和实验验证本文方法的有效性和可行性。
1 虚拟同步发电机与下垂控制原理分析
为保证合适的功率均分和提高系统的可靠性,微电网传统下垂控制模拟电力系统发电机的行为,通过DG的频率和电压调整自身输出功率[12],是一种有效的控制策略。传统的下垂控制利用有功功率、无功功率值调节逆变器的输出频率和电压幅值,具体如下:

(1)
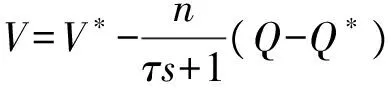
(2)
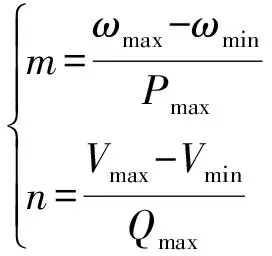
(3)
式中:ω*和V*分别为DG在额定状态下的频率和幅值;P*和Q*分别为有功和无功额定容量;τ为功率低通滤波器的滤波参数;m和n分别为有功和无功下垂增益;P和Q分别为DG在实际频率ωi和电压Ei条件下输出的有功功率和无功功率值;ωmin和ωmax分别为系统频率最小值和最大值;Pmin和Pmax分别为DG输出的最小值和最大值。
将式(1)改写为:
(4)
相对于传统同步发电机的转子方程,转动惯量J和阻尼系数D可以表达为:

(5)
根据式(5)可知,低通滤波参数τ起到虚拟惯性的作用。因此,一阶低通滤波器实现了功率控制和电压控制在时间尺度上的差异化,提高了DG逆变器的惯性和系统稳定性。
DG逆变器的控制框图见附录A图A1,由功率外环和电压、电流双闭环控制构成,其中功率外环实现多DG的有功和无功功率的均分控制性能。本文引入虚拟阻抗控制,用于有功、无功控制的解耦和减少DG线路参数差异化的影响。此外,虚拟阻抗还可以在暂态过程中增加功率振荡阻尼,而不影响有功功率分配精度[12]。
2 自适应虚拟惯性控制算法
在传统电力系统中,当发生功率供需不平衡时,同步发电机可以缓慢释放转子转动动能(约10 s),从而具有较强的抗干扰能力。然而,对于微网逆变器而言,其响应速度约为10 ms,若DG是采用传统的下垂控制,频率会随着负载的变化而快速变化。因此,要求DG的控制策略不仅要模拟一次频率控制,而且要模拟出系统惯性,避免系统频率出现突变或很大偏差。
系统大惯性可以减少暂态过程中的频率偏差,但需要较大的储能容量。系统小惯性具有很快的响应速度,并保证暂态过程的功率均分,然而在大扰动和系统突变的情况下,小惯性系统却容易导致电压和频率出现严重偏差,从而影响系统稳定性和可靠性。为了综合两者的优点,当频率偏离时,系统应该显示出很大的惯性,而在恢复频率时呈现低惯量,如附录A图A2所示。
因此,本文提出了一种自适应虚拟惯性的控制策略,其虚拟惯量J的表达式为:

(6)
式中:J0为DG的虚拟初始惯量;表达式右边项(ω-ω*)dω/dt为自适应虚拟惯性项;k为调节系数。由于频率变化ωs=ω-ω*和频率变化率dω/dt同号时,表示需增加惯性以减少频率的偏差,频率变化ωs和频率变化率dω/dt异号时,表示需减少惯性以快速恢复频率。因此,无论ωs和dω/dt怎样变化,本文算法设计的k的取值需大于0。
将式(6)代入式(4)和式(5)时,可得到改造后的动态摇摆方程为:
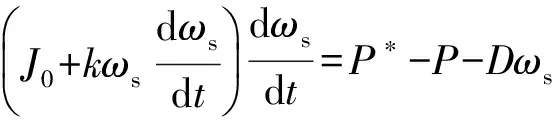
(7)
显然式(7)是关于dωs/dt的一元二次方程。根据韦达定理,且考虑系统频率与频率变化率乘积应有正负号,故舍掉一个根,得到方程的解为:

(8)
式中:ΔP=P*-P。
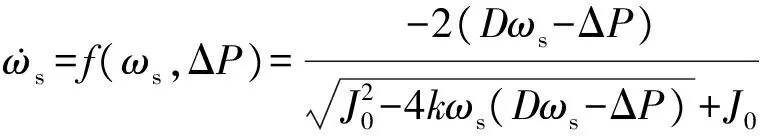
(9)
若将式(9)代入式(6),使自适应虚拟惯性中不含频率的微分项,在算法实现时避免了系统噪声的干扰,有利于系统的稳定。此外,本文的自适应虚拟惯性调节具有平滑连续性,简单实用。
3 基于自适应虚拟惯性的控制策略的收敛性和稳定性分析
3.1 收敛性分析
为分析本文提出的基于自适应虚拟惯性的控制方法的收敛性,可将式(7)简化描述为:
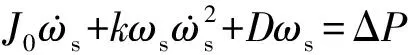
(10)
式中:ωs为系统的状态变量,有功功率P为负荷需求。而ΔP为系统的输入变量,决定系统的平衡位置[17-18]。
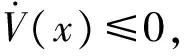
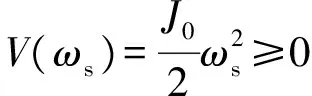
(11)
由于输入变量不影响系统稳定性,忽略式(9)中ΔP的影响,同时方程两边同乘以频率滑差ωs,可以得到:
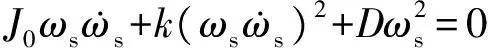
(12)

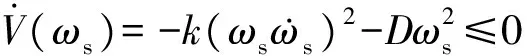
(13)
因此,通过式(13)表明:由于系数k>0,阻尼D>0,本文提出的基于自适应虚拟惯性的有功—频率控制策略是收敛的。
3.2 稳定性分析
从式(7)和式(9)可看出,构造的自适应虚拟惯性具有典型非线性的特征,利用传统的稳定性分析方法较为复杂[20-21]。为了简化分析,本文假设单机微源相对于微电网的容量比较小,公共母线近似看做一个容量较大的电源,利用电力系统的单机无穷大母线模型分析所提出的自适应虚拟惯性算法的收敛性。附录A图A3为一台DG通过电抗为Xl的线路并联至公共母线的示意图。
逆变器输出端连接配置LCL滤波器,从而改变了低压微电网的线路参数属性。此外,虚拟电抗也可等效同步增加DG的输出阻抗值[22]。此时电源的输出功率为:
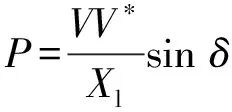
(14)
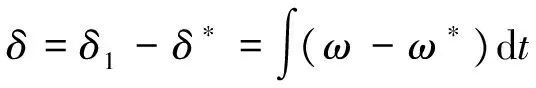
(15)
式中:V和δ1分别为DG输出电压幅值和相角;Xl为DG线路等效电抗;δ为功角,δ*为其初始值。
联立式(9)、式(14)和式(15),可以得到:

(16)
利用状态空间模型对式(16)重新描述,可以得到模型为:
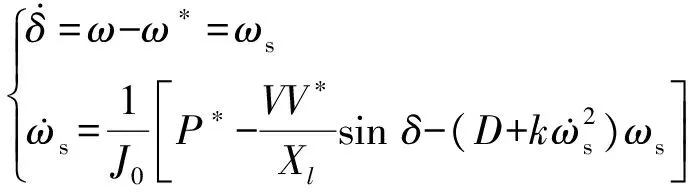
(17)
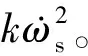
那么选择状态变量[x1,x2]T=[(δ-δ0),ωs]T,式(17)可以重新表示为:
(18)
其中,δ0,a,b参数表达式分别为:
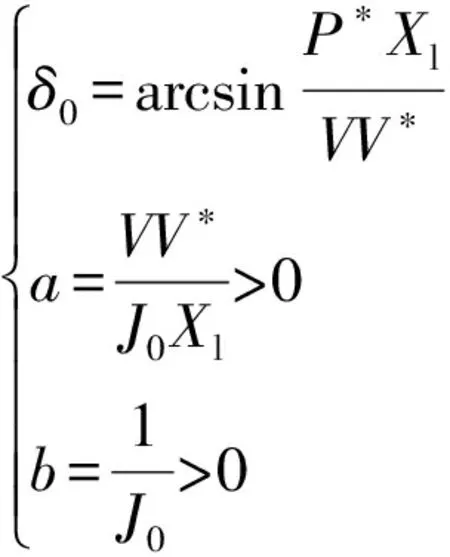
(19)
那么,本文构造的系统李雅普诺夫函数为:

(20)
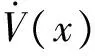

(21)
综合上述式(20)和式(21),得到系统的稳定域为:
-π+δ0≤δ≤π-δ0
(22)
此外,不适当的虚拟惯量也容易引起多DG之间的功率振荡问题。因此,有必要综合考虑惯性和阻尼共同作用下的频率动态问题。忽略自适应虚拟惯性的正阻尼项,即k=0,将式(16)线性化得到:

(23)
式(23)为一种典型的二阶系统,则系统的自然振荡频率和阻尼比必须满足如下关系式:
(24)
所以,根据式(24)可得,系统的阻尼比取决于系统的运行状态、虚拟初始惯量J0和阻尼系数D,因此需合理设计这些参数保证系统的稳定运行,详细参数分析见第4节。
4 系统参数综合分析
4.1 系统储能容量与惯量值之间的参数分析
根据上述式(7)—式(9),系统稳定时方程的根应该为一个实数,并考虑系统的有功输入,得到方程的解为:
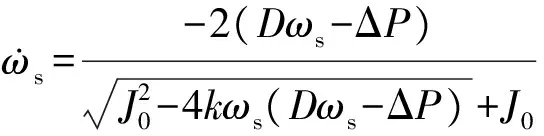
(25)
本文在实现所提的控制方法时,可直接通过式(25)实现。式(25)中已经不含频率的微分项,避免了引入系统噪声,更有利于系统稳定。此外,在暂态过程中式(26)所示条件必须成立。
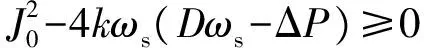
(26)
由式(4)可知,当系统达到稳态时,频率的变化率为零,所以有
Dωs=ΔP=P*-P
(27)
不妨假设系统从一个平衡状态(ωs1,P1)到另一个平衡状态(ωs2,P2)过程中,由于DG不能短时匹配负荷需求,则增加的储能容量可在此过程中提供能量缓冲和惯性,有功功率P1和P2为两种平衡状态下DG的输出。对于平衡状态1,不妨设置系统的自适应虚拟惯量为J0,于是可得到:
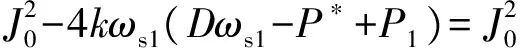
(28)
Dωs1=ΔP1=P*-P1
(29)
当微电网系统负荷从P1变化到P2时,则增加的系统储能容量缓冲为(P2-P1),由于虚拟初始惯量J0的存在使得系统频率不能瞬时变化,综合式(28)和式(29),系统的方程可变为:
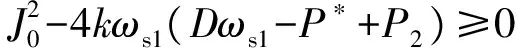
(30)
联立上述方程式(28)—式(30),可得到:

(31)
根据式(31)可知,当平衡状态1的负荷需求P1=0时,可得到系统允许最大功率为:

(32)
所以,系统从一个平衡状态(ωs1,P1)到另一个平衡状态(ωs2,P2)过程所需要的最小储能容量Ps为:
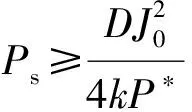
(33)
因此,式(33)表明了系统储能容量与惯量值之间的参数关系。此外,为了实现高功率快速充放电,一般考虑的储能容量方案可选择电池和超电容器复合储能系统,超级电容提供瞬时高功率,电池提供长时间的功率缺额[23-25],本文不再详细阐述。
4.2 自适应惯性控制关键参数分析
自适应惯性控制关键参数主要是指阻尼系数D、稳态时的惯量J0和调节系数k,下面给出具体设计原则。
1)根据传统的下垂控制表达式(式(1)—式(3))可知,当系统频率限定在[ωmin,ωmax]范围内时,要使系统稳定运行在允许的范围内,则有功下垂控制参数满足:
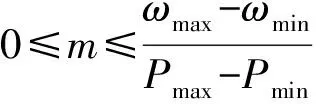
(34)
又根据式(5),得到阻尼系数D的取值范围为:

(35)
2)根据式(24)所示系统二阶方程需满足的性能要求,虚拟初始惯量J0和系统响应阻尼比ζ之间的关系为:
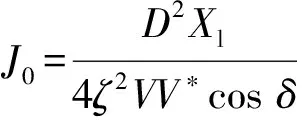
(36)
根据阻尼比的取值范围ζ∈ [0.1,0.8]、物理参数Xl和阻尼系数D,可以近似求出虚拟初始惯量J0的取值范围为:
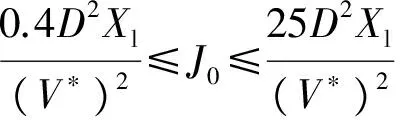
(37)
3)考虑式(25)方程有解,且为实数(非复数)的条件,要保证自适应虚拟惯性算法的稳定有效,下式需要恒成立:
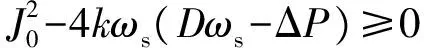
(38)
尤其在两种极端情况下(功率输出最大和输出最小)需满足:
(39)
系统稳定时,存在稳态解为:

(40)
结合式(35)和式(40),式(38)和式(39)可以化简为:
(41)

那么,调节系数k的取值范围可以表示为:
(42)
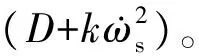
5 仿真和实验
5.1 仿真验证
为验证本文提出的基于自适应虚拟惯性的微电网动态频率稳定控制策略的可行性,基于MATLAB/Simulink软件平台搭建了微电网系统的仿真模型。整个微电网仿真系统则由两个相同容量的逆变型DG并联连接,微电网系统的额定频率和电压幅值分别为50 Hz和311 V。系统馈线参数为Z1=(0.82+j1.2)Ω,Z2=(1.0+j1.56)Ω,负荷有功功率为2 kW,无功功率为2 kvar,Lf=3 mH,Cf=20 μF。具体DG的参数如附录A表A1所示。图1为本文采用的基于自适应虚拟惯性控制的改进功率外环仿真模型示意图。
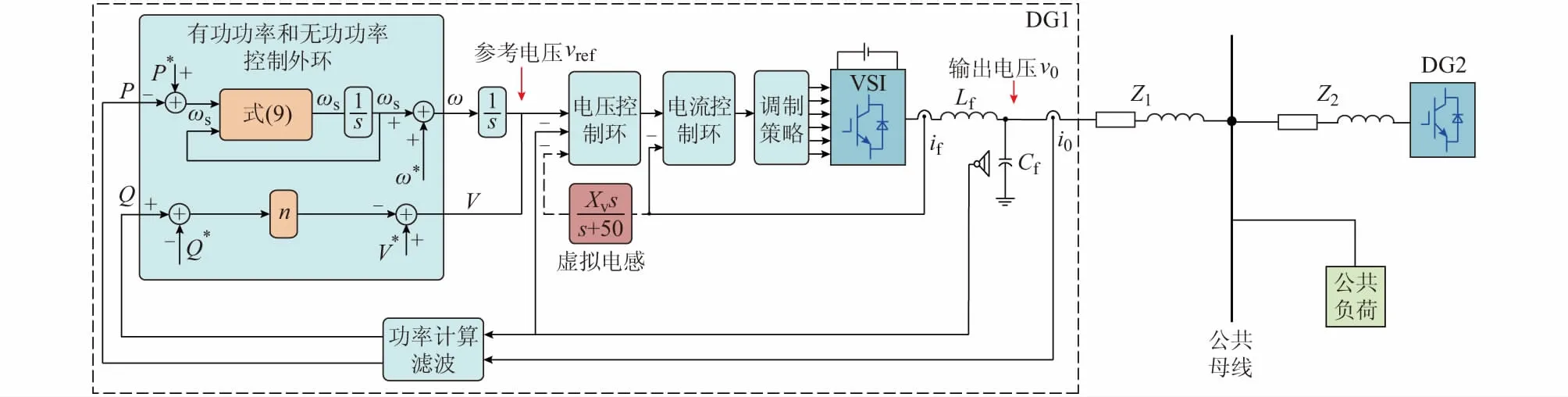
图1 基于自适应虚拟惯性控制的改进功率外环仿真模型Fig.1 Simulation model for improved power outer loop based on adaptive virtual inertia control algorithm
5.1.1仿真案例1
图2为微电网系统在负荷变化时仿真的功率结果图,为了体现本文提出的自适应虚拟惯性控制算法的优越性,共进行了3组仿真对比,其中图2(a)为采用传统下垂控制的小惯性调节仿真波形(J0=10,k=0),图2(b)为采用大惯性调节的虚拟同步发电机仿真波形(J0=100,k=0),图2(c)为采用自适应虚拟惯性调节的虚拟同步发电机仿真波形(J0=100,k=0.18),从3幅功率结果图中可看出,功率的动态响应具有近似的总体趋势,不过仍然存在差异:小惯性情况下的功率响应基本不存在振荡,动态性能良好;大惯性情况下的功率响应尽管存在数个周期振荡,但由于传统的虚拟初始惯量J0已经按照式(37)经过合理化选择,已具备一定的抗功率振荡能力,整体动态性能一般;当采用本文提出的自适应虚拟惯性方法,尽管固有参考惯性与大惯性情况下相同,但在补偿调节系数k的有效作用下,功率振荡得到了减弱,提高了系统的暂态稳定性。
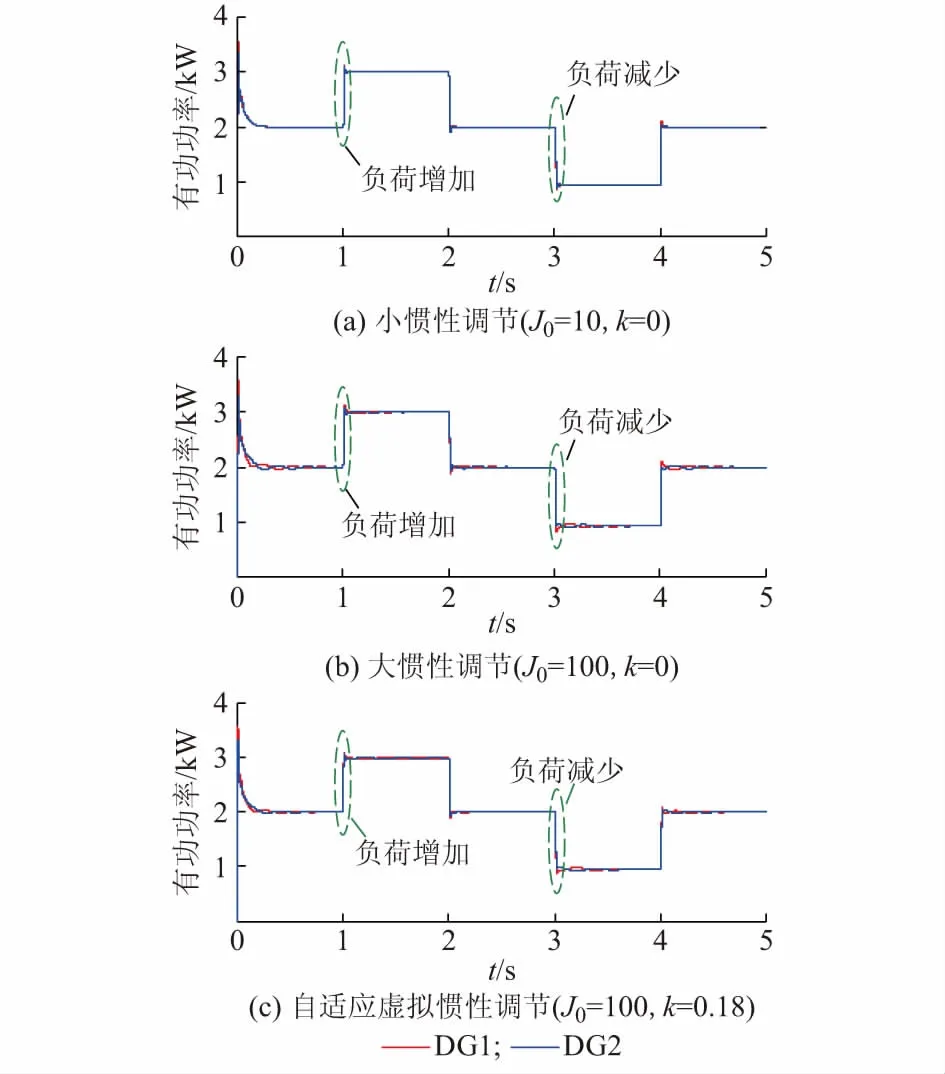
图2 负荷变化时仿真的功率结果图(案例1)Fig.2 Simulation results of active power under load variation (case 1)
图3为微电网系统在负荷变化时仿真的频率和惯量结果图,为了体现本文提出的自适应虚拟惯性控制算法的优越性,共进行了小惯性调节、大惯性调节和自适应惯性调节3组仿真对比。在图3(a)中,本文提出的自适应虚拟惯性方法在负载切换的动态过程中具有强鲁棒性。与传统的小惯性下垂控制相比较,系统频率偏离额定值的速度慢;与大惯性的虚拟同步发电机相比,系统频率恢复速度快,因此,自适应虚拟惯性控制算法兼顾了小惯性和大惯性的优点,有效提高了系统的暂态稳定性。
在图3(b)中,小惯性调节和大惯性调节系数的数值分别恒定为10和100,当采用本文提出的自适应虚拟惯性控制方法,等效虚拟惯性在频率偏离额定值时具有大惯性,在频率向额定值恢复时具有小惯性,能够根据实际运行状况自适应调节。另外,从横坐标放大的缩影图(仿真时间3.99~4.1 s)中看出,由于避免了直接采样角频率微分项,自适应惯性的调节使等效惯量中不再包含任何断续型的微分项,只与运行角频率和输出功率相关,因此系统的自适应虚拟惯性调节具有平滑连续的特性,增强了系统抗干扰的能力,更加有利于系统的稳定。
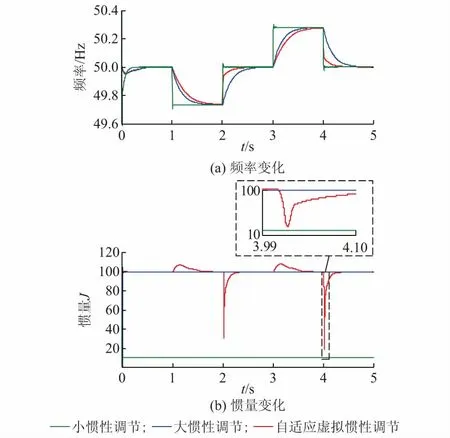
图3 负荷变化时频率和惯量的仿真结果(案例1)Fig.3 Simulation results of frequency and inertia under load variation (case 1)
5.1.2仿真案例2
为进一步验证本文提出的自适应虚拟惯性控制方法的性能,进行了在负荷频繁波动条件下的3组仿真对比。图4为微电网系统在负荷频繁波动条件下仿真的频率和惯量结果图。在图4(a)中,当采用本文提出的自适应虚拟惯性控制方法,当负荷频繁波动时,系统频率的最大变化量为0.1 Hz;大惯性情况下系统频率的最大变化量为0.3 Hz,而在小惯性情况下频率的最大变化量为0.6 Hz。因此,本文提出的方法相对大惯性和小惯性情况,系统频率变化范围小,能有效提高系统的暂态稳定性。
在图4(b)中,当采用本文提出的自适应虚拟惯性控制方法,DG的惯量随着负荷的变化而变化,等效虚拟惯量在频率偏离额定值时具有大惯性,在频率向额定值恢复时具有小惯性,能够根据实际运行状况自适应调节,其变化范围为[30,120],正是由于这种自适应的惯性调节,保证了系统的频率变化小,提高了系统的抗干扰能力和稳定性。
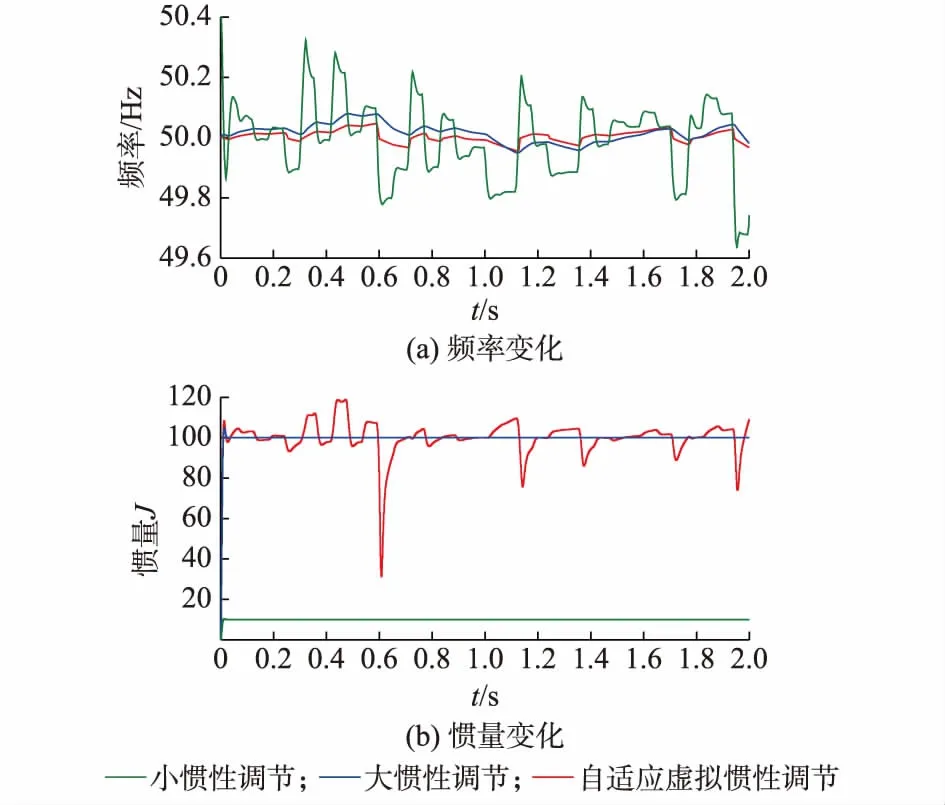
图4 负荷频繁波动时频率和惯量的仿真结果(案例2)Fig.4 Simulation results of frequency and inertia when frequent load fluctuates (case 2)
5.2 实验验证
为验证本文提出的方法,建立了一套2台DG并联运行的微电网系统实验样机,如附录A图A4所示。其主电路开关器件采用绝缘栅双极型晶体管(IGBT)器件,控制板核心由芯片DSP28335和现场可编程门阵列(FPGA)构成。样机微电网系统的额定频率、电压幅值分别为50 Hz和96 V。其中,补偿调节系数k=1.05,小惯性调节时J0=4,大惯性调节时J0=30,其他控制参数见附录A表A1。
附录A图A5(a)为采用传统下垂控制的小惯性调节实验波形(J0=4,k=0),图A5(b)为采用大惯性调节的虚拟同步发电机实验波形(J0=30,k=0),图A5(c)为采用自适应虚拟惯性的虚拟同步发电机实验波形(J0=30,k=0.18)。从3幅功率结果图中看出:具有相同惯性的2台DG在不同惯性控制策略条件下的功率动态响应具有近似的总体趋势。因此,说明本文提出的自适应虚拟惯性控制策略不影响DG的功率动态响应能力,且具有快速的响应速度。
图5为负荷变化时系统频率和惯量的实验波形。在图5(a)中,当系统频率偏离额定值50 Hz时,采用自适应虚拟惯性控制方法,系统频率偏离额定值的速度较慢;而当系统频率恢复额定值50 Hz时,系统频率恢复速度快。因此,本文方法在负载切换的动态过程中具有更强的鲁棒性。在图5(b)中,当采用本文提出的自适应虚拟惯性控制方法,虚拟惯量在频率偏离额定值时具有大惯性,在频率向额定值恢复时具有小惯性,能够根据实际运行状况自适应调节。因此,本文方法具有平滑连续的特性,并增强了系统抗干扰的能力。

图5 负荷变化时系统频率和惯量实验波形Fig.5 Experiment waveforms of system frequency and inertia under load variation
6 结语
本文在分析微电网中传统下垂控制和虚拟同步发电机控制的基础上,为了提高微电网频率的动态稳定性,提出了一种基于自适应虚拟惯性的同步发电机的控制策略,该方法模拟同步发电机的行为,构造频率变化率与虚拟惯性的关系,自适应改变虚拟同步发电机控制的惯性。
本文利用李雅普诺夫稳定理论分析了DG采用所提算法的收敛性和稳定性。仿真和实验结果表明了本文方法的有效性和可行性。本文提出的基于自适应虚拟惯性的同步发电机控制策略可实现频率动态控制,快速恢复频率,减缓频率偏离额定值,有效提高了系统的暂态稳定性和抗干扰能力,为含波动型负荷和不确定输出微源的微电网系统提供了新的解决方案。下一步工作将研究基于自适应虚拟惯性算法的多分布式微电源并联及系统稳定性问题。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] 鲁宗相,王彩霞,闵勇,等.微电网研究综述[J].电力系统自动化,2007,31(19):100-107.
LU Zongxiang, WANG Caixia, MIN Yong, et al. Overview on microgrid research[J]. Automation of Electric Power Systems, 2007, 31(19): 100-107.
[2] 王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.
WANG Chengshan, LI Peng. Development and challenges of distributed generation, the micro-grid and smart distribution system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.
[3] GUERRERO J M, CHANDORKAR M, LEE T L, et al. Advanced control architectures for intelligent microgrids: Part Ⅰ decentralized and hierarchical control[J]. IEEE Transactions on Industrial Electronics, 2013, 60(4): 1254-1262.
[4] 杨新法,苏剑,吕志鹏,等.微电网技术综述[J].中国电机工程学报,2014,34(1):57-70.
YANG Xinfa, SU Jian, LÜ Zhipeng, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70.
[5] 杜威,姜齐荣,陈蛟瑞.微电网电源的虚拟惯性频率控制策略[J].电力系统自动化,2011,35(23):26-31.
DU Wei, JIANG Qirong, CHEN Jiaorui. Frequency control strategy of distributed generations based on virtual inertia in a microgrid[J]. Automation of Electric Power Systems, 2011, 35(23): 26-31.
[6] 杨向真,苏建徽,丁明,等.微电网孤岛运行时的频率控制策略[J].电网技术,2010,34(1):164-168.
YANG Xiangzhen, SU Jianhui, DING Ming, et al. Research on frequency control for microgrid in islanded operation[J]. Power System Technology, 2010, 34(1): 164-168.
[7] 吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34(16):2591-2603.
LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.
[8] 张玉治,张辉,贺大为,等.具有同步发电机特性的微电网逆变器控制[J].电工技术学报,2014,29(7):261-268.
ZHANG Yuzhi, ZHANG Hui, HE Dawei, et al. Control strategy of micro grid converters with synchronous generator characteristic[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 261-268.
[9] ASHABANI M, MOHAMED Y A R I. Novel comprehensive control framework for incorporating VSCs to smart power grids using bidirectional synchronous-VSC[J]. IEEE Transactions on Power Systems, 2014, 29(2): 943-957.
[10] XIONG Liansong, ZHUO Fang, WANG Feng, et al. Static synchronous generator model: a new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(9): 6264-6280.
[11] ANDRADE F A, ROMERAL L, CUSIDO J, et al. New model of a converter-based generator using electrostatic synchronous machine concept[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 833-840.
[12] 刘尧,林超,陈滔,等.基于自适应虚拟阻抗的交流微电网无功功率-电压控制策略[J].电力系统自动化,2017,41(5):16-21.DOI:10.7500/AEPS20160428017.
LIU Yao, LIN Chao, CHEN Tao, et al. Research on reactive power-voltage control strategy of AC microgrid based on adaptive virtual impedance[J]. Automation of Electric Power Systems, 2017, 41(5): 16-21. DOI: 10.7500/AEPS20160428017.
[13] GUAN Minyuan, PAN Wulue, ZHANG Jing, et al. Synchronous generator emulation control strategy for voltage source converter (VSC) stations[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3093-3101.
[14] LIU J, MIURA Y, ISE T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3600-3611.
[15] SONI N, DOOLLA S, CHANDORKAR M C. Improvement of transient response in microgrids using virtual inertia[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1830-1838.
[16] ALIPOOR J, MIURA Y, ISE T. Power system stabilization using virtual synchronous generator with alternating moment of inertia[J]. IEEE Journal of Emerging Selected Topics in Power Electronics, 2015, 3(2): 451-458.
[17] ARANI M F M, MOHAMED Y A R I, El-SAADANY E F. Analysis and mitigation of the impacts of asymmetrical virtual inertia[J]. IEEE Transactions on Power Systems, 2014, 29(6): 2862-2874.
[18] URIARTE F M, SMITH C, VANBROEKHOVEN S. Microgrid ramp rates and the inertial stability margin[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3209-3216.
[19] 程冲,杨欢,曾正,等.虚拟同步发电机的转子惯量自适应控制方法[J].电力系统自动化,2015,39(19):82-89.DOI:10.7500/AEPS20141130003.
CHENG Chong, YANG Huan, ZENG Zheng, et al. Rotor inertia adaptive control method of VSG[J]. Automation of Electric Power Systems, 2015, 39(19): 82-89. DOI: 10.7500/AEPS20141130003.
[20] 徐海珍,张兴,刘芳,等.基于微分补偿环节虚拟惯性的虚拟同步发电机控制策略[J].电力系统自动化,2017,41(3):96-102.DOI:10.7500/AEPS20160420001.
XU Haizhen, ZHANG Xing, LIU Fang, et al. Control strategy of virtual synchronous generator based on differential compensation virtual inertia[J]. Automation of Electric Power Systems, 2017, 41(3): 96-102. DOI: 10.7500/AEPS20160420001.
[21] HE Jinwei, LI Yunwei, GUERRERO J M, et al. An islanding microgrid power sharing approach using enhanced virtual impedance control scheme[J]. IEEE Transactions on Power Electronics, 2013, 28(11): 5272-5282.
[22] 韩华,刘尧,孙尧,等.一种微电网无功均分的改进控制策略[J].中国电机工程学报,2014,34(16):2639-2648.
HAN Hua, LIU Yao, SUN Yao, et al. An improved control strategy for reactive power sharing in microgrids[J]. Proceedings of the CSEE, 2014, 34(16): 2639-2648.
[23] TORRES L M A, LOPES L A C, MORAN T L A. Self-tuning virtual synchronous machine: a control strategy for energy storage systems to support dynamic frequency control[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 833-840.
[24] DELILLE G, FRANCOIS B, MALARANGE G. Dynamic frequency control support by energy storage to reduce the impact of wind and solar Generation on isolated power system’s inertia[J]. IEEE Transactions on Sustainable Energy, 2012, 4(3): 931-939.
[25] HAN Yi, YOUNG P M, JAIN A, et al. Robust control for microgrid frequency deviation reduction with attached storage system[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 557-565.
刘 尧(1987—),男,硕士,工程师,主要研究方向:电力电子、微电网控制技术。
陈建福(1965—),男,博士,教授级高级工程师,主要研究方向:电力系统分析及微电网控制技术。
侯小超(1990—),男,博士研究生,主要研究方向:微电网控制及其稳定性分析。
粟 梅(1967—),女,通信作者,教授,博士生导师,主要研究方向:新能源发电与现代电力电子系统建模、优化与控制。E-mail: sumeicsu@mail.csu.edu.cn

