虚拟同步发电机的暂态稳定性分析
朱 蜀, 刘开培, 秦 亮
(武汉大学电气工程学院, 湖北省武汉市 430072)
0 引言
虚拟同步发电机通过模拟传统同步发电机的摇摆方程实现换流器的虚拟惯性控制,其在大扰动下的稳定性值得关注[1]。虚拟同步发电机是由电力电子器件及非线性的控制系统构成的装置,本质上属于非线性非自治系统,对于这样的系统,小信号分析是分析其稳定性的重要手段[2-3]。然而,小信号分析只能分析系统在稳态工作点附近的稳定性,而不能研究大扰动下系统的全局动态特性。
近年来,由电力电子装置及其构成的系统的暂态稳定性开始得到研究。文献[4-5]指出三相整流器在交流电网电压跌落时,可能发生不可逆转的不稳定现象,使系统在故障结束后无法回到正常工作点,并分别基于分岔分析和混合电势方法分析了故障前后换流器的稳定性。文献[6]建立了暂态稳定分析时间尺度下的全功率机组降阶模型,并且利用等面积法对全功率机组进行暂态稳定性分析。文献[7-8]定义了逆变器的虚拟功角,得出逆变器电流未饱和时的虚拟功角特性和电流饱和下的虚拟功角特性,并在此基础上分析了逆变器的虚拟功角同步稳定机理。文献[9-11]对由多换流器构成的微电网的暂态稳定性进行了研究。
由于各种非线性因素的相互作用,虚拟同步发电机暂态作用下的演变研究遇到了挑战[1]。目前,对非线性系统的研究主要有两种:一种是李雅普诺夫函数方法,文献[12]基于系统的简化模型,建立了能源路由器的李雅普诺夫函数,它的缺点是对一般非线性系统难以构造李雅普诺夫函数;另一种是时域仿真法,文献[13]基于系统详细模型和降阶模型通过时域仿真法研究了电力电子接口电源的暂态稳定性,这种方法的缺点是计算量过大。因此利用高效的方法对系统进行全局分析很有必要。在此情形下,本文引入胞映射方法对虚拟同步发电机大扰动下的稳定性进行分析。这种方法最早由文献[14]提出,在当前的计算机硬件条件下,可以更有效地解决高维非线性动力学复杂系统问题,定量描述非线性体系中的那些全局动态特征,并确定非线性系统的动力学机制。文献[15-16]分别应用胞映射方法对单机无穷大系统和交直流系统进行系统稳定域的评估。
在电力电子装置的暂态稳定机理研究上,文献[4-5,17]都认为大扰动下系统存在不可逆的分岔现象。文献[6-7,18-19]则认为系统在大扰动下存在类似于传统同步发电机的动力学失稳现象,本文研究的是虚拟同步发电机的动力学失稳现象。文献[20-21]都提出了提升电力电子系统暂态稳定性的控制策略,然而其暂态稳定机理有待进一步揭示。
本文的目的在于研究虚拟同步发电机的暂态稳定性,验证了以状态空间平均模型(下文亦称为大信号模型)分析虚拟同步发电机暂态稳定性的有效性,并基于奇异摄动理论建立起虚拟同步发电机暂态稳定性分析的9阶和3阶简化模型,分别用于虚拟同步发电机的吸引域计算和暂态失稳机理分析,其次引入了胞映射方法分析虚拟同步发电机的暂态稳定性,减少了计算量并求解出文献[1]提到的电力电子装置吸引域。本文方法的合理性通过MATLAB/Simulink仿真进行验证。
1 虚拟同步发电机的建模
1.1 虚拟同步发电机控制策略
采用虚拟同步发电机控制的换流器典型拓扑[22]如图1所示(图中PI为比例—积分环节),通过在控制策略中引入同步发电机的机械和电磁方程,使得换流器的外特性模拟成传统的同步发电机。正因为同步发电机机械方程的引入,使得换流器在大扰动下可能出现类似同步发电机的暂态失稳现象。
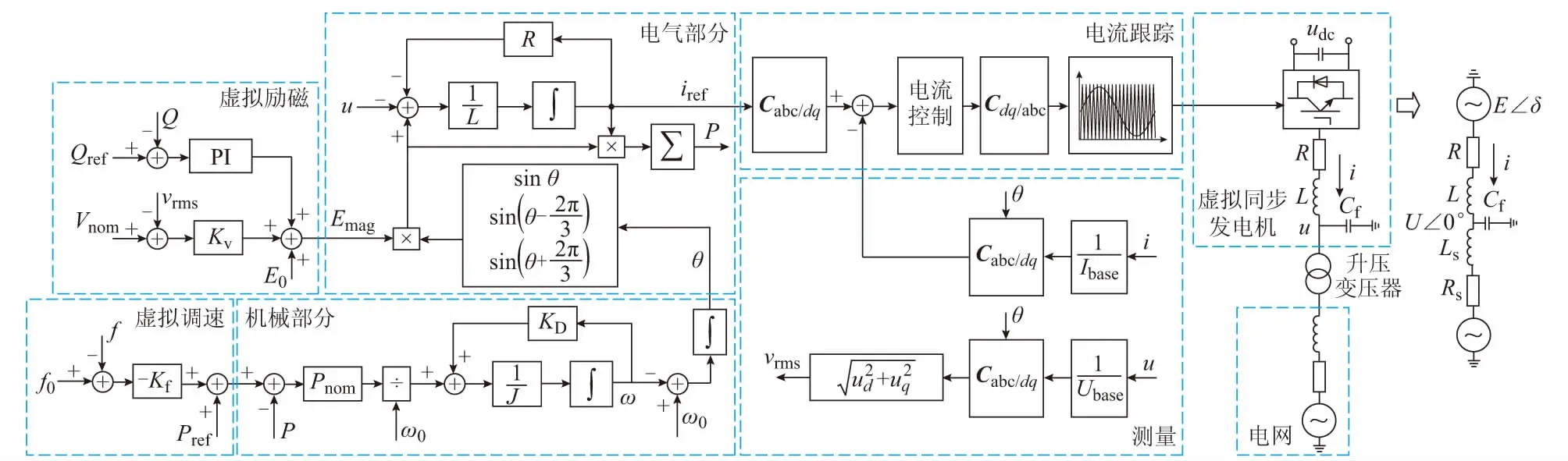
图1 虚拟同步发电机拓扑及控制策略Fig.1 Topology and control strategy of virtual synchronous generator
值得指出的是,本文的分析建立在忽略换流器继电保护装置的影响上,也就是假定换流器在大扰动期间持续运行且不采取额外控制措施。虚拟同步发电机采用的控制策略主要包括测量、虚拟励磁、虚拟调速、电气部分、机械部分和电流跟踪,电流控制采用双环解耦控制中的电流内环控制,电流控制的输出经过坐标变换送入PWM调制器。
1.2 虚拟同步发电机的完整大信号模型
电力电子装置本质上是拓扑时变的,在稳定工作时,系统的各个变量也在不同状态进行切换,因此系统实际上不存在平衡点。除了电力电子装置的详细模型,状态空间平均模型也被广泛应用于电力电子装置的暂态稳定性分析,如DC/DC变换器、电压源型换流器及双馈风机大扰动下的稳定性分析[4-8,23-26]。本文同样通过状态空间平均建模和Park变换建立起系统的大信号模型,进而分析系统平衡点的渐进稳定性。通过后续分析可以表明,大信号模型用于暂态稳定性分析时能保留电力电子装置大扰动下的基本动态特性。
本文在进行虚拟同步发电机大信号建模时采用幅值不变的Park变换。系统和控制坐标系的转换见附录A图A1,两个坐标系变量的转换关系为:
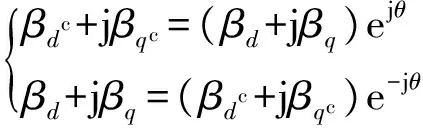
(1)
式中:βd和βq分别为交流电压或电流在d-q轴的分量;βdc和βqc分别为控制器中交流电压或电流在d-q轴的分量;θ为两个坐标系相差的角度,在稳态时为零。
为了方便后面的建模,将式(1)写成式(2)的形式。系统中电气量通过Tf1转化为控制量,控制量通过Tf2转化为电气量。
(2)
系统在标幺值下的功率计算如式(3)所示。
(3)
式中:ed和eq分别为换流器内电势在d-q轴的分量;irefd和irefq分别为控制器电气部分的输出,即参考电流在d-q轴的分量。
调制器和交流系统的建模如式(4)和式(5)所示,具体建模过程可以参考文献[27-28]。

(4)
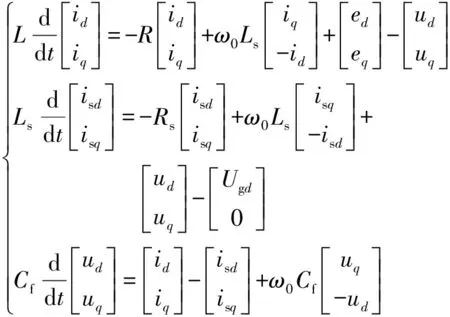
(5)
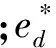
将各个模块的方程联合,可以得到虚拟同步发电机的完整大信号模型,如附录A图A2所示,完整模型的阶数为15阶,具体的状态变量及编号见附录A表A1。
1.3 模型的降阶
系统中变量的动态常可以按时间尺度分为慢动态和快动态,在分析系统的稳定性时,如果考虑系统所有动态会使分析变得复杂,也是不必要的。下文将基于奇异摄动理论进行降阶,其简介如下。
系统至少包含两种时间尺度的动态过程。即
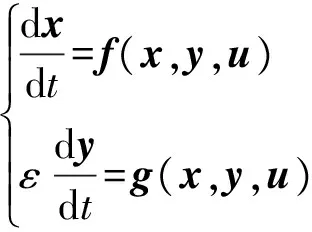
(6)
式中:f和g分别为慢动态变量和快动态变量的微分方程组中的函数;x为主导慢动态变量;y为随动快动态变量;u为输入参数;ε为奇异摄动参数,一般为杂散电感、电容等。
在运动轨迹任一点x=x0附近,只要矩阵∂g/∂y|x=x0,所有特征根实部为负值,则约束流形g=0就保持对快动态y的吸引性。此时高阶系统式(6)可降阶为:
(7)
根据文献[13],可以通过分析系统特征根的实部来对快慢时间尺度进行划分,本文根据附录A表A2所示的虚拟同步发电机参数建立模型,系统的特征根分布与特征根关联变量见附录A表A3。
从附录A表A3可以看到,系统中的慢动态特征根包括{λ11,λ12,…,λ15},如果保留这5个慢动态特征根对应的状态变量,则可以建立经典微分代数方程(DAE)降阶模型。然而文献[13]表明,采用混合DAE降阶模型(即慢动态的个数大于慢特征根数)与经典DAE降阶模型相比可以提高运算的精度,类似结论也可以从文献[26]找到,因此本文共保留9个状态变量。剩下的9个状态变量主要包括控制器中的积分变量及虚拟同步发电机输出电流,具体为[z3,θ,z2d,z2q,iq,ω,id,z1d,z1q],属于慢动态和混合动态,如果继续降阶将导致动态特性与原系统产生较大差异,后文分析亦可以验证此结论。
此外9阶模型仍然不利于虚拟同步发电机的暂态失稳机理分析,为探明系统暂态失稳的症结,本文建立了虚拟同步发电机的3阶模型(见附录B),后续分析表明,由[z3,θ,ω]构成的3阶模型同样可以模拟出虚拟同步发电机的暂态失稳现象,从后文分析可以看到,3阶模型中功率与虚拟功角的非线性关系是导致虚拟同步发电机暂态失稳的主要原因。
1.4 模型的验证
本文将各个阶数的模型与电磁暂态仿真模型进行对比,系统参数见附录A表A2,对比结果见附录A图A3。系统在4.5 s时发生交流电压跌落,跌落深度为50%,持续时间为0.2 s。从附录A图A3可见,采用15阶和9阶模型可以较好地模拟系统动态特性,采用5阶和3阶模型造成电流等快动态特性的仿真精度的缺失,然而其阶数低,仍能较准确地保留虚拟同步发电机的外特性,适于机理分析。
2 胞映射方法在暂态稳定性分析中的应用
2.1 胞映射方法的基本原理
由于非线性问题目前尚没有统一的分析方法, 因此在对系统进行全局分析时,数值方法一直占有重要的地位。直接对代数微分方程进行数值求解可以研究动力系统的全局特性,要确定相空间中系统的吸引域, 可以以某一初始点进行数值积分, 当充分长时间后系统的最终运动行为就确定了吸引子的位置, 而所有可以到达该吸引子的初始点的集合就构成了该吸引子的吸引域。这种方法计算量很大,每个初始点需要经过足够长的积分时间才能对吸引域进行准确求解。而胞映射方法则可以更加高效地对吸引域进行求解,在高维强非线性系统的全局性态分析上更有优势。
简单胞映射算法的基本流程如附录C图C1所示,其详细流程可以参考文献[14]。算法的核心思想是将连续状态空间离散化为许多小的几何体(胞),每个胞视为系统状态的一个独立实体,因此状态空间离散化为大量胞的集合。胞的集合构成胞状态空间并且被整序数所标识。对每一个胞的中心点进行短时积分(映射),则可以建立该胞与积分结果所在的胞的映射关系, 从而就构造出一个基于胞空间上的映射。对胞映射动力系统进行分析, 可求得运动方程的稳态解及其吸引域。简单胞映射就是每个胞实体只有一个映射像胞的映射,系统的演化由胞到胞的映射来描述。
2.2 虚拟同步发电机吸引域
下面将胞映射方法用于9阶模型的全局动态特性分析。因为分析的系统是高维系统,所以本文选取吸引域的两个截面来观察虚拟同步发电机的全局动态特性。将系统的稳定工作点记为xe,除了系统角频率ω和θ外其余的状态变量都取xe中对应的值时,吸引域截面记为Se;除了ω和θ外其余的状态变量都取0时,吸引域截面记为S0。两个截面的吸引域如图2所示。图2(a)为通过胞映射方法求得的Se截面的吸引域,图2(b)为根据求得的吸引域描绘的稳定边界。从图2(b)可见,当初始点位于吸引域内时,虚拟同步发电机角频率和功角经过振荡衰减逐渐回到原来的稳定工作点;而当虚拟同步发电机发生大扰动导致系统状态变量运行到吸引域外时,故障切除后系统也无法回到原来的工作点,功角不断增大,出现失稳现象。下文将分析虚拟同步发电机暂态稳定性的影响因素,并精确计算虚拟同步发电机的故障临界切除时间(CCT)。
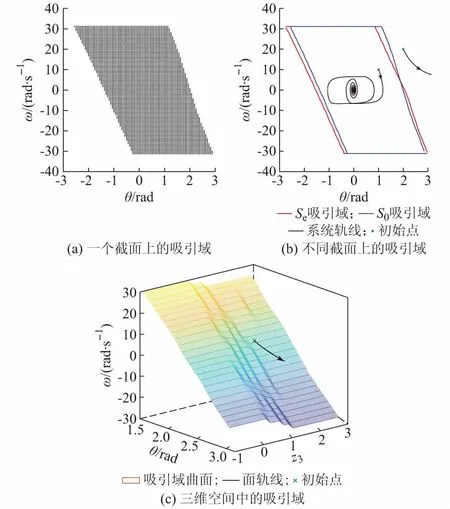
图2 虚拟同步发电机吸引域Fig.2 Attraction domain of virtual synchronous generator
2.3 失稳机理分析
文献[7]通过分析功率外环,研究了下垂控制逆变器的暂态失稳机理,本文通过对模型进行逐级降阶探寻虚拟同步发电机暂态失稳的症结。从下文的系统特征根分布可以看出,当系统参数发生改变时,特征根λ11和λ12可能从左半平面移动到右半平面,附录C图C2进一步给出了特征根λ11和λ12中各个状态变量的参与程度,可以看到状态变量x3和x8(即ω和θ)在这两个模态中的参与程度最高,可以认为其对虚拟同步发电机的稳定性影响最大。下面将上文建立的3阶模型用于验证这一结论,通过本文方法求出该模型的吸引域曲面如图2(c)所示,模型的降阶及3阶模型中保留的状态变量z3会对吸引域的精确求解产生一定影响,但是3阶模型仍能反映出虚拟同步发电机的暂态失稳机理,虚拟角速度和虚拟功角对稳定性的影响最大,在一定范围内,其他状态变量对吸引域曲面的影响较小。附录C图C3采用不同阶数模型估计的吸引域边界,可以发现使用低阶模型会使刻画的吸引域面积偏大。
为进一步分析虚拟同步发电机的暂态失稳机理,将3阶模型进一步地简化,简化过程见附录B,最终可以得到式(8)。
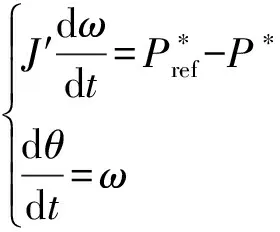
(8)
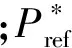
P*=
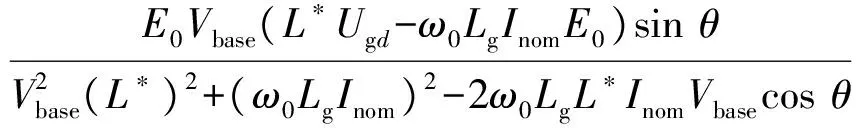
(9)
式中:E0为虚拟同步发电机额定输出电压幅值;Vbase为虚拟同步发电机电压基准值;Ugd为电网电压在d轴的分量;Lg为电网电感;L为换流器电感;L*为换流器电感标幺值;Inom为虚拟同步发电机额定电流。
根据式(9)画出虚拟同步发电机的功角曲线见图3,当电网阻抗为零时,可以发现虚拟同步发电机模型与传统同步发电机类似,功角曲线为标准正弦曲线;当电网阻抗不为零时,功率与功角呈现图3所示的非线性关系,虽然此时功角曲线不是标准的正弦波,但是根据交流同步发电机理论,在功角曲线顶点的右半边系统仍然是不稳定的。当电网电压发生跌落时,可以画出虚拟同步发电机在不同时刻的功角曲线,利用等面积法则可以发现,当交流电压发生跌落时,虚拟转子先加速然后减速,如果故障过程中加速面积A1大于减速面积A2,虚拟同步发电机将出现类似于传统同步发电机中的“失步”现象,若不采取任何措施,控制器内的虚拟功角将不断增大。
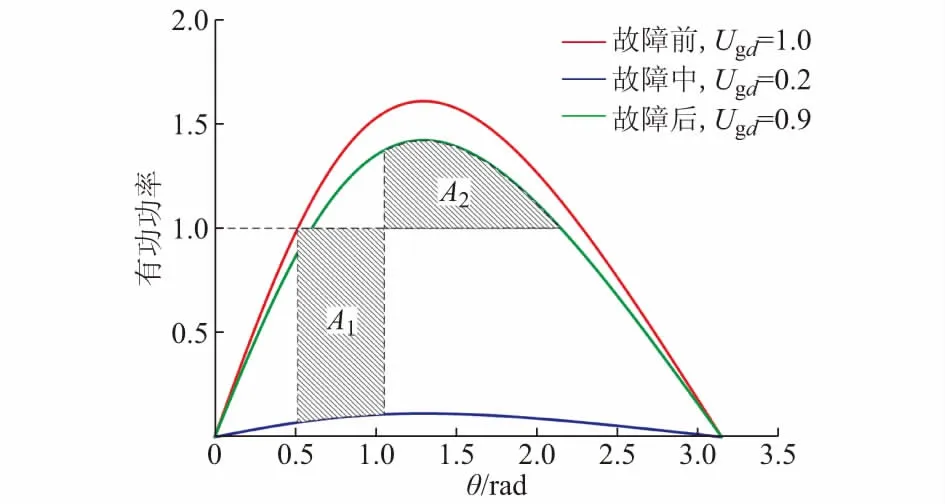
图3 虚拟同步发电机暂态失稳示意图Fig.3 Diagram of transient stability of virtual synchronous generator
图3也可以为虚拟同步发电机的暂态稳定性提升策略提供一些思路,如果能在电流电压发生跌落时检测到电压跌落,在故障期间减小虚拟同步发电机的参考功率Pref(图3中Pref=1.0(标幺值))并配合虚拟同步发电机的低电压穿越措施就可以避免暂态失稳现象的发生,本文不再展开这方面的内容。
3 大扰动下的稳定性分析
3.1 小信号分析
系统大扰动后重新回到工作点的前提是工作点附近小扰动稳定,本文先对虚拟同步发电机进行小信号分析,分析系统参数的取值范围。将上文建立的大信号模型线性化即可得到系统的小信号模型。
文献[2,5]表明,系统参数如电网阻抗、虚拟同步发电机输送功率、虚拟惯量、阻尼系数和滤波电容等会对虚拟同步发电机的稳定性产生影响。本文分析了这些参数对系统稳定性的影响,小信号分析结果见附录D图D1。随着电网阻抗、输送功率、虚拟惯量和滤波电容的增加及阻尼系数的减小,系统都有可能出现正实部特征根,导致系统小信号不稳定。CCT常作为衡量同步发电机暂态稳定性的指标,下文分析表明,小信号分析可能得出和CCT指标矛盾的结论。
3.2 大信号分析
通过小信号分析可以得到系统中参数的取值范围,然而在非线性系统中,小信号分析无法得出系统稳定程度的定量信息,根据主导极点只能判断平衡点附近系统的稳定性,无法判断系统大扰动下的暂态特性。根据系统的吸引域可以观察系统参数变化时系统稳定边界的变化趋势,在一定程度上可以分析系统的稳定裕度。如附录D图D2所示,电网阻抗、输送功率、虚拟惯量、阻尼系数和滤波电容都将对吸引域产生较显著的影响,仿真结果同样可以验证这一结论。
系统在故障期间虚拟功角和虚拟角速度总是向相平面的右上方偏移,观察附录D图D2中第一象限的吸引域大小可以发现,吸引域的变化趋势与小信号分析一致;然而此时仍然无法得出这些参数对CCT的影响情况,这是因为CCT由两方面决定,一是系统工作点到稳定边界(在传统同步发电机中可以理解为临界切除角或者临界能量,在虚拟同步发电机中理解为吸引域边界)的距离,二是故障期间状态变量的变化快慢(系统的积分时间常数)。吸引域仍然只能得出前者的信息,后者需要对系统进行时域仿真才能得出。从后面的仿真可以看到,系统工作点在离吸引域边界较远的情形下仍然可能有较小的CCT。
下文将给出吸引域的精确刻画及CCT求解方法。此外,根据式(8)和式(9)可以从理论上解释电网阻抗及输送功率对虚拟同步发电机暂态稳定性的影响。根据式(9)画出不同电网阻抗对功角曲线的影响如图4所示,电网阻抗对虚拟同步发电机的暂态稳定性的影响直观体现在虚拟同步发电机的功角曲线上,在相同的输送功率情况下,随着电网阻抗的增大,虚拟同步发电机的暂态稳定裕度减小,即可减速面积减小。此外,可以观察到系统输送功率增大时也将导致稳定裕度减小。图中Pref1=3(标幺值),Pref2=5。
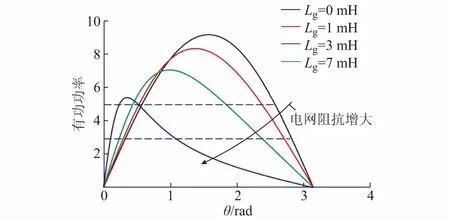
图4 电网阻抗和输送功率的影响机理Fig.4 Influence mechanism of grid impedance and transmission power
3.3 吸引域的精确刻画及CCT求解
仍然通过虚拟角速度和虚拟功角构成的相平面观察系统的吸引域,关键在于其他状态变量的值如何确定。本文采取的方法为对模型进行时域仿真,大致确定虚拟同步发电机的CCT,选取系统恰未失稳时刻的状态变量值作为系统的初始工作点,由前述分析可知,在较小范围内,其他状态变量的变化对吸引域的影响较小,此时由虚拟角速度和虚拟功角刻画的吸引域是较为精确的。在得出精确的吸引域之后,对模型进行积分、观察虚拟功角和虚拟角速度的偏移量,系统轨线跨越吸引域边界时可以认为系统将发生暂态失稳,此时的时刻确定为CCT。
4 仿真结果与讨论
通过仿真附录E表E1中的4组参数来验证本文的结论,未列出的参数见附录A表A2。首先,通过算例1来验证虚拟同步发电机中的暂态失稳现象,如图5所示。在3.2 s时交流电压跌落到0,从图5(a)可见,当故障切除时间为0.16 s时,系统经过衰减振荡重新回到稳定工作点;而如果故障持续到0.17 s时再切除,则系统无法重新回到原来的工作点,虚拟转子角速度高于电网电压角速度,虚拟同步发电机和电网电压的功角差不断变大。
下面验证本文提出的吸引域精确刻画方法。虚拟功角和虚拟角速度随时间变化的相图如图5(b)所示,相轨迹与吸引域的对比如图5(c)所示,可以看到当状态变量偏移到吸引域边界外时便发生暂态失稳现象,无法再回到稳定工作点。
电网阻抗、输送功率和虚拟惯量对临界切除时间的影响如附录E图E1所示。不同的算例仅一个变量改变,与算例1相比,算例2的电网阻抗减小,算例3的输送功率减小,算例4的虚拟惯量增加。从附录E图E1可见,随着电网阻抗和输送功率的减小,系统在故障持续时间为0.17 s时能保持稳定。值得指出的是随着虚拟惯量的增加,虚拟同步发电机的CCT增加,然而从附录D图D1(c)的小信号分析可知,随着虚拟惯量的增大,系统的主导极点向右半平面移动,系统将出现不稳定现象,这一矛盾现象已经在第3.2节中进行分析。在传统同步发电机中,以单机无穷大系统为例,同步发电机的惯量并不会对系统的稳定边界(临界切除角)产生影响(见文献[29]第13章),然而惯量大的同步发电机会有较大的CCT,这是符合直觉的,因为惯量大的发电机组的功角和转速变化较慢。虚拟惯量虽然对吸引域有一定影响,但是同样会影响模型的积分时间常数,对比算例4与算例1的波形可以发现,同样的故障持续时间,大的虚拟惯量会使虚拟角速度和虚拟功角变化更慢,从而可能导致更大的CCT。
同样可以画出不同算例时域仿真曲线的相平面图及对应的吸引域边界,如附录E图E2所示,其中实线为相轨迹,点划线为吸引域边界。从附录E图E2可见,算例1的相轨迹跨越吸引域边界后出现暂态失稳现象,而其他算例的相轨迹则在吸引域边界内,因此在故障后能重新回到稳态工作点。
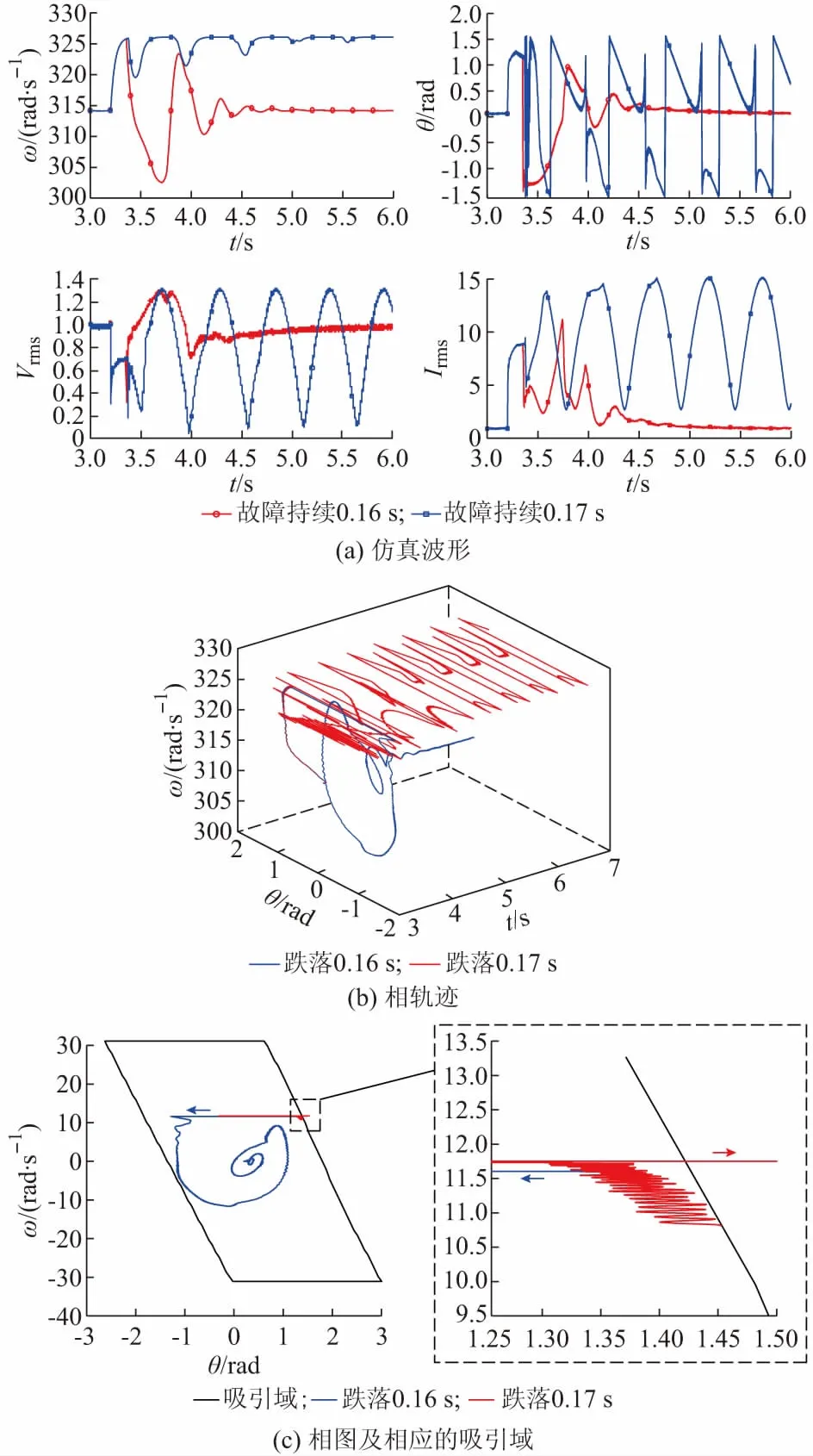
图5 不同故障切除时间对比Fig.5 Comparison of different fault clearing time
本文提出的虚拟同步发电机CCT求解方法的验证见附录E表E2,其中时域仿真的测试间隔为0.005 s,从附录E表E2可见,本文方法基本准确。
5 结论
本文研究了单机无穷大连线方式下虚拟同步发电机的暂态稳定性,其结论及下一步研究工作展望如下。
1)虚拟同步发电机在大扰动下存在类似于同步发电机中的功角失稳现象,且受到系统参数的影响。电网阻抗、滤波电容和输送功率的增加及阻尼系数和虚拟惯量的减小将导致这种现象更加容易出现。
2)状态空间平均建模和坐标变换建立的非线性微分代数方程可以较准确地描述虚拟同步发电机在大扰动下的运行特性;基于奇异摄动理论可以根据不同时间尺度对系统进行降阶,其中包含虚拟功角和虚拟角速度的3阶模型便能反映出这种失稳现象;虚拟同步发电机中功率与虚拟功角的非线性关系是导致暂态失稳的重要非线性环节。
3)基于胞映射方法的虚拟同步发电机全局动态特性分析可以研究虚拟同步发电机在大扰动下的运行特性。但是降阶后的模型仍然面临很大的计算量,计算量随着系统维数的增加呈指数增长,改进胞映射算法或采用并行计算可以提高计算效率。
4)多虚拟同步发电机中的暂态失稳机理比单机无穷大连线方式下更加复杂,其暂态稳定性的体现及失稳机理的分析是下一步研究工作的重点。此外,电力电子装置具有灵活可控的特点,从本文分析可见,控制器是导致失稳的关键因素,如何在大扰动下对换流器进行控制来避免此种现象的发生也值得进一步研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] 朱蜀,刘开培,秦亮,等.电力电子化电力系统暂态稳定性分析综述[J].中国电机工程学报,2017,37(14):3948-3962.
ZHU Shu, LIU Kaipei, QIN Liang, et al. Analysis of transient stability of power electronics dominated power system:an overview[J]. Proceedings of the CSEE, 2017, 37(14): 3948-3962.
[2] CHEN D, XU Y, HUANG A Q. Integration of DC microgrids as virtual synchronous machines into the AC grid[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7455-7466.
[3] MO O, D’ARCO S, SUUL J A. Evaluation of virtual synchronous machines with dynamic or quasi-stationary machine models[J]. IEEE Transactions on Industrial Electronics, 2016, 64(7): 5952-5962.
[4] 彭宇,黄萌,查晓明,等.三相电压源型换流器故障耐受能力分析与评估[J].电力系统自动化,2016,40(18):109-115.DOI:10.7500/AEPS20160128004.
PENG Yu, HUANG Meng, ZHA Xiaoming, et al. Fault tolerance ability analysis and evaluation of three-phase voltage source converters[J]. Automation of Electric Power Systems, 2016, 40(18): 109-115. DOI: 10.7500/AEPS20160128004.
[5] HUANG M, PENG Y, CHI K T, et al. Bifurcation and large-signal stability analysis of three-phase voltage source converter under grid voltage dips[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8868-8879.
[6] 张琛,蔡旭,李征.全功率变换风电机组的暂态稳定性分析[J].中国电机工程学报,2017,37(14):4018-4026.
ZHANG Chen, CAI Xu, LI Zheng. Transient stability analysis of wind turbines with full-scale voltage source converter[J]. Proceedings of the CSEE, 2017, 37(14): 4018-4026.
[7] 黄林彬,章雷其,辛焕海,等.下垂控制逆变器的虚拟功角稳定机理分析[J].电力系统自动化,2016,40(12):117-123.DOI:10.7500/AEPS20150709007.
HUANG Linbin, ZHANG Leiqi, XIN Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123. DOI: 10.7500/AEPS20150709007.
[8] 章雷其,黄林彬,黄伟,等.提高下垂控制逆变器虚拟功角暂态稳定性的控制方法[J].电力系统自动化,2017,41(12):56-62.DOI:10.7500/AEPS20170125007.
ZHANG Leiqi, HUANG Linbin, HUANG Wei, et al. Control methods for improving virtual power angle transient stability of droop-controlled inverters[J]. Automation of Electric Power Systems, 2017, 41(12): 56-62. DOI: 10.7500/AEPS20170125007.
[9] 帅智康,邹福筱,涂春鸣,等.微网暂态稳定性研究[J].电力系统自动化,2015,39(16):151-159.DOI:10.7500/AEPS20141118002.
SHUAI Zhikang, ZOU Fuxiao, TU Chunming, et al. Review on transient stability of microgrid[J]. Automation of Electric Power Systems, 2015, 39(16): 151-159. DOI: 10.7500/AEPS20141118002.
[10] KABALAN M, SINGH P, NIEBUR D. Large signal Lyapunov-based stability studies in microgrids: a review[J]. IEEE Transactions on Smart Grid, 2017, 8(6): 2287-2295.
[11] ZHANG Y, XIE L. A transient stability assessment framework in power electronic-interfaced distribution systems[J]. IEEE Transactions on Power Systems, 2016, 31(6): 5106-5114.
[12] SUN Q, ZHANG Y, HE H, et al. A novel energy function-based stability evaluation and nonlinear control approach for energy internet[J]. IEEE Transactions on Smart Grid, 2017, 8(3): 1195-1210.
[13] 叶一达,魏林君,阮佳阳,等.电力电子接口电源的准功率特性降阶建模体系[J].中国电机工程学报,2017,37(14):3993-4001.
YE Yida, WEI Linjun, RUAN Jiayang, et al. A generic reduced-order modeling hierarchy for power-electronic interfaced generators with the quasi-constant-power feature [J]. Proceedings of the CSEE, 2017, 37(14): 3993-4001.
[14] HSU C S. Applied mathematical sciences: cell-to-cell mapping[M].Germany: Springer, 1987.
[15] APIWON P, HSU C S. Domain of stability of synchronous generators by a cell mapping approach[J]. International Journal of Control, 1985, 41(5): 1253-1271.
[16] FERNANDOPULLE N, ALDEN R. Domain of stability of AC/DC power systems[J]. Canadian Journal of Electrical and Computer Engineering, 2007, 32(4): 215-220.
[17] 阮佳阳,鲁宗相,乔颖,等.并网型双馈异步发电机奇异诱导分岔型电压崩溃机理[J].中国电机工程学报,2014,34(31):5467-5476.
RUAN Jiayang, LU Zongxiang, QIAO Ying, et al. Study on voltage collapse caused by singularity-induced bifurcation of grid-connected doubly-fed induction generators [J]. Proceedings of the CSEE, 2014, 34(31): 5467-5476.
[18] KIM H J, KANG S W, SEO G S, et al. Large-signal stability analysis of DC power system with shunt active damper[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6270-6280.
[19] XIONG L, LIU X, WANG F, et al. Static synchronous generator model for investigating dynamic behaviors and stability issues of grid-tied inverters[C]// Applied Power Electronics Conference and Exposition, March 20-24, 2016, Long Beach, USA: 2742-2747.
[20] HART P J, LASSETER R H, JAHNS T M. Symmetric droop control for improved hybrid AC/DC microgrid transient performance[C]// Energy Conversion Congress and Exposition, September 18-22, 2017, Milwaukee, USA.
[21] HOU X, HAN H, ZHONG C, et al. Improvement of transient stability in inverter-based AC microgrid via adaptive virtual inertia[C]// Energy Conversion Congress and Exposition, September 18-22, 2017, Milwaukee, USA.
[22] 吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34(16):2591-2603.
LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.
[23] YING J, YUAN X, HU J. Inertia characteristic of DFIG-based WT under transient control and its impact on the first-swing stability of SGs[J]. IEEE Transactions on Energy Conversion, 2017, 32(4): 1502-1511.
[24] HU T. A nonlinear-system approach to analysis and design of power-electronic converters with saturation and bilinear terms[J]. IEEE Transactions on Power Electronics, 2011, 26(2): 399-410.
[25] SIEWNIAK P, GRZESIK B. A brief review of models of DC-DC power electronic converters for analysis of their stability[J]. International Journal of Electronics, 2014, 101(10): 1405-1426.
[26] KABALAN M, SINGH P, NIEBUR D. Nonlinear Lyapunov stability analysis of seven models of a DC/AC droop controlled inverter connected to an infinite bus[J/OL]. IEEE Transactions on Smart Grid[2017-09-20]. http://ieeexplore.ieee.org/document/8036269/.
[27] 杨洁,刘开培,余俞,等.交流电网互联的双端柔性直流输电系统小信号建模[J].中国电机工程学报,2015,35(9):2177-2184.
YANG Jie, LIU Kaipei, YU Yu, et al. Small signal modeling for VSC-HVDC used in AC grid interconnection[J]. Proceedings of the CSEE, 2015, 35(9): 2177-2184.
[28] 杨洁,刘开培,王东旭,等.向无源网络供电的双端柔性直流输电系统小信号稳定性分析[J].中国电机工程学报,2015,35(10):2400-2408.
YANG Jie, LIU Kaipei, WANG Dongxu, et al. Small signal stability analysis of VSC-HVSC applied to passive network[J]. Proceedings of the CSEE, 2015, 35(10): 2400-2408.
[29] PRABHA KUNDUR.电力系统稳定与控制[M].北京:中国电力出版社,2002.
朱 蜀(1994—),男,博士研究生,主要研究方向:电力电子化电力系统暂态稳定性分析。E-mail: whuzhushu@whu.edu.cn
刘开培(1962—),男,教授,博士生导师,主要研究方向:直流输电技术、电能质量及非线性控制技术。E-mail: kpliu@whu.edu.cn
秦 亮(1980—),男,通信作者,博士,副教授,主要研究方向:大功率电力电子技术及其应用、柔性直流输电系统和风电并网。E-mail: qinliang@whu.edu.cn

