松弛小功角约束条件的虚拟同步发电机功率解耦策略
李明烜, 王 跃, 徐宁一, 周 晖, 雷万钧
(电力设备电气绝缘国家重点实验室(西安交通大学), 陕西省西安市 710049)
0 引言
目前,以逆变器作为并网接口的风电、光伏等分布式电源发展迅速,渗透率不断提高,使得电网的惯性和阻尼不足、电压和频率支撑能力变弱等问题越来越突出,这严重限制了分布式电源的并网容量[1-5]。为解决此问题,虚拟同步发电机(virtual synchronous generator,VSG)的概念被提出[5-11]。VSG作为一种适合并网逆变器广泛接入的有前景的控制策略,近年来已成为新能源领域的研究热点[12-13]。
VSG通过下垂控制实现对频率和电压自动独立调节,因此VSG继承了传统下垂控制中存在的功率耦合问题[14-15]。下垂控制能有效工作的基本条件是传输线路接近纯感性且功角满足小功角近似条件[16]。然而,分布式电源往往会连接到低压或中压网络中,其阻抗比R/X往往较大。而且在许多情况下,如逆变器发生较大扰动时,小功角近似会产生较大误差。这两方面都会造成有功功率和无功功率发生耦合,进而影响功率的控制精度、动态响应以及系统稳定性。同时,由于VSG引入了虚拟惯量控制,其内在特性决定了VSG可能会产生有功功率振荡[7,17]。如果有功功率和无功功率控制环之间存在耦合,振荡会在两个环路之间传递,使无功功率也随着有功功率振荡,增加两个功率环在动态调节过程中的振荡幅值和调节时间,严重时甚至使控制失效而引发振荡发散[18]。相比传统同步发电机而言,并网逆变器的过流能力差,往往不能承受较大的功率振荡。因此,功率耦合对于VSG的影响比采用下垂控制的逆变器以及同步发电机都要严重,需要重点解决。
为了解决线路阻抗比较大引起的功率耦合,学者们提出了许多改进的下垂控制策略,主要可分为四大类:基于虚拟阻抗[19]、基于虚拟有功和无功功率坐标变换[20]、基于虚拟频率和电压坐标变换[21]以及基于电压前馈补偿[15,22]的解耦策略。这些方法可以较好地消除高线路阻抗比R/X对功率耦合的影响,但很少有文献探讨和解决小功角约束条件对于功率耦合的影响。文献[14-15]基于相对增益法分析了微网中的耦合机理,并分别提出了基于前馈和对角矩阵的解耦策略,但所提解耦策略仍然是以小功角条件为前提的近似解耦。文献[18]同时考虑到了线路阻抗比和功角对VSG有功和无功控制的影响,从优化设计阻尼系数的角度提出了VSG功率振荡抑制的方法。文献[23]通过小信号建模,分析了VSG中存在的动态耦合现象,并通过引入虚拟电阻抑制耦合引起的振荡。但文献[18,23]均没有从根本上解除有功功率和无功功率控制环之间的耦合,由功率耦合本身引起的稳态误差和稳定裕度降低等问题依然存在。文献[22]通过修改励磁电压调节器实现对公共耦合点(PCC)电压的精确跟踪来满足功率解耦的需求,但这种方法对线路阻抗参数辨识的精确度要求较高。
为解决上述问题,本文首先分析了VSG的功率耦合特性,并讨论了线路阻抗比和功角对于VSG功率耦合的作用。然后,本文提出了一种可松弛小功角约束条件的功率解耦方案,实现了更加精确的功率解耦控制。通过与传统方案的对比分析,证明了提出的解耦方法可以更有效地减弱有功环与无功环之间的耦合作用;同时证明了提出的解耦方法可以增加系统的增益裕度和相位裕度,增强了VSG系统的稳定性。最后,通过实验验证了所提方法的有效性。
1 基本的VSG控制策略
本文所研究的VSG模型的控制框图和主电路如图1(a)所示。分布式电源通过一个三相电压源型逆变器并入交流母线,控制策略在d-q坐标系下实现。功率控制环产生输出电压指令的幅值和频率。虚拟阻抗与电压控制环模拟同步发电机定子绕组的电气特性。电流控制环采用比例—积分(PI)调节器,实现电流的精确跟踪以及过电流保护。图中:vabc和iabc分别为VSG的三相输出电压和输出电流;vdq和idq分别为VSG输出电压和输出电流d轴和q轴分量;Pref和Qref分别为有功功率和无功功率指令;E为VSG的虚拟内电势,模拟了同步发电机的内电势;ω为有功控制环产生的虚拟内电势的角频率。

图1 基本VSG控制框图Fig.1 Block diagram of control of basic VSG
功率控制环是VSG的核心。其中,有功功率控制环包含图1中P-ω下垂和虚拟惯性控制两部分,控制框图如附录A图A1(a)所示。
P-ω下垂控制模拟了同步发电机一次调频功能:
Pm=Pref-mp(ω-ωref)
(1)
式中:Pref为上层调度给出的有功指令;Pm为下垂控制输出的虚拟机械功率,作为后级虚拟惯量环节的有功指令;mp为P-ω下垂系数。
在P-ω下垂控制的后级,引入虚拟惯量控制模拟同步发电机的转子惯性:

(2)
式中:P为输出有功功率;M=Jωref为惯性系数,其中J为虚拟转动惯量;D为阻尼系数。
综合式(1)和式(2),有功功率控制环可以写为:

(3)
无功功率控制采用Q-E下垂,模拟同步发电机的电压调节特性,产生VSG虚拟内电势的幅值,框图如附录A图A1(b)所示。无功功率控制环表达式为:
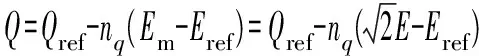
(4)
式中:nq为Q-E下垂系数;Em为VSG虚拟内电势的幅值;Eref为输出电压额定幅值;Qref为额定电压下的无功功率;Q为输出无功功率。
根据式(3)和式(4)可知,VSG分别通过控制VSG输出电压的频率(功角)和幅值来实现对输出有功功率和无功功率的各自独立的解耦控制。
2 VSG控制的功率耦合问题
VSG经阻感性线路连接到交流电网的等效电路如附录A图A2所示。线路中传输的有功和无功功率可用式(5)表示[18]:

(5)
式中:E和V分别为VSG内电势和交流母线处电压的有效值;δ为功角;R和X分别为VSG与交流母线间的等效电阻和感抗。
从式(5)中可以看出,有功功率和无功功率均为功角和电压幅值的二元函数。将式(5)在稳态工作点处进行线性化和小信号建模,得到:


(6)
式中:γc=δ+arctan(R/X);δ0和E0分别为稳态工作点处的功角和内电势有效值。
式(6)表明当γc≠0时,有功功率和无功功率是相互耦合而不是彼此独立的。
相对增益分析(Bristol-Shinskey方法) 是一种有效的量化耦合程度方法[24]。其原理如下:设yi为多变量系统的一个被控制变量,uj为一个控制变量,将uj到yi通道相对增益定义为通道在其他通道均断开时的通道增益pij(第一放大系数)与该通道在其他通道均闭合且其他被控制量均不变的通道增益qij(第二放大系数)之比,即
(7)
式中:pij为第j个控制变量到第i个被控制变量的第一放大系数,pij按矩阵位置排列可构成对应的第一放大系数矩阵P;qij为第j个控制变量到第i个被控制变量的第二放大系数,qij按矩阵位置排列可构成对应的第二放大系数矩阵Q;c为常数。
将相对增益λij按矩阵位置排列,可构成多变量控制系统对应的相对增益矩阵(RGA),其描述了整个多变量系统的耦合关系及程度。该矩阵具有每行及每列的元素之和为1的性质。
根据相对增益矩阵的定义,可以直接通过第一放大系数矩阵P的矩阵运算得到相对增益矩阵[24]:
Λ=P⊗(P-1)T
(8)
式中:Λ为相对增益矩阵;⊗表示矩阵对应元素相乘。
本文的研究对象VSG有功功率和无功功率控制环是一个两输入两输出系统。式(6)已经给出了其第一放大系数矩阵P。因此根据式(8),可以推导得出输入到输出的相对增益矩阵为:
(9)
式中:λ11=λ22=cos2γc,表征了δ-P和E-Q控制通道的相对增益;λ12=λ21=1-λ11=sin2γc,表征了δ-Q和E-P耦合通道的相对增益。它们的大小反映了系统有功环和无功环的耦合程度。
根据相对增益矩阵的性质,只有当λ11满足在(0.5,1]区间(即λ12满足在[0,0.5)区间)时,才能保证δ-P和E-Q的配对关系,即保证功率控制环的有效性;而λ11越接近于1(即λ12越接近于0),表示系统的耦合越弱,解耦控制效果越好。当λ11<0.7(即λ12>0.3) 时,表示系统的耦合已经非常严重[24]。
综上,为了量化耦合程度,本文定义相对耦合系数Kc为:
(10)
由式(10)可以看出,功率的耦合程度与功角及线路阻抗比有关,Kc越大,表示系统的耦合越强。
图2(a)给出了耦合系数与功角和阻抗比的三维关系图,其中粉色线代表耦合系数为1时的等高线。在粉色线的左侧,耦合系数随着阻抗比或功角的增大而增大,功率耦合程度加剧;而在粉色线的右侧,耦合系数则随着阻抗比或功角的增大而减小,这主要是因为在粉色线的右侧,功角与阻抗角之和大于90°,根据正弦函数的特性,进一步增大阻抗比或功角将导致耦合系数减小。由于实际运行中,功角是从0°开始增加的,在耦合系数增大并越过粉色线之前,系统已经失去稳定,故而在实际工况中逆变器不可能稳定运行在粉色线右侧的区域。

图2 耦合系数与阻抗比和功角的关系Fig.2 Relationship between coupling coefficient and impedance ratio and power angle
图2(b)给出了在满足小功角近似的条件(δ≈0°)下阻抗比与耦合系数的关系曲线,可以看出当阻抗比等于0.65时,耦合系数为0.3,此时系统功率已经存在严重的耦合,而随着阻抗比的进一步增大,功率耦合程度加剧。当阻抗比大于1时,耦合系数大于0.5,耦合通道对输出功率的影响占主导地位。
图2(c)给出了在满足阻抗比R/X=0时功角与耦合系数的关系曲线。同样,可以看出当功角等于0.58 rad时,耦合系数为0.3,此时系统功率已经存在严重的耦合,并随着功角的增大,耦合程度加剧。当功角大于0.78 rad时,耦合系数大于0.5,耦合通道对输出功率的影响大于控制通道的影响。
综上分析可知,功率耦合由线路阻抗比和功角共同产生,传统基于小功角约束条件的下垂控制策略只是近似解耦。事实上,当VSG在欠阻尼条件下,系统发生扰动时往往会引发较大的功角振荡,使得功角容易运行到较大功角的工作点。同时,有功环的振荡特性通过耦合通道会引起无功功率的振荡,并进一步耦合到有功环路中,对系统的耦合起到放大作用。因此,为了保证系统的控制性能和稳定性,功角引起的耦合作用不容忽略,需要解决此问题。
3 松弛小功角约束条件的功率解耦策略
为了同时解决线路高阻抗比以及小功角近似引起的功率耦合问题,提出了如图3所示的松弛小功角约束条件的功率解耦策略。该策略共分为虚拟稳态同步阻抗和松弛小功角约束条件的电流前馈动态解耦两个部分,分别对应于图1中虚拟阻抗和电流控制两个环节。
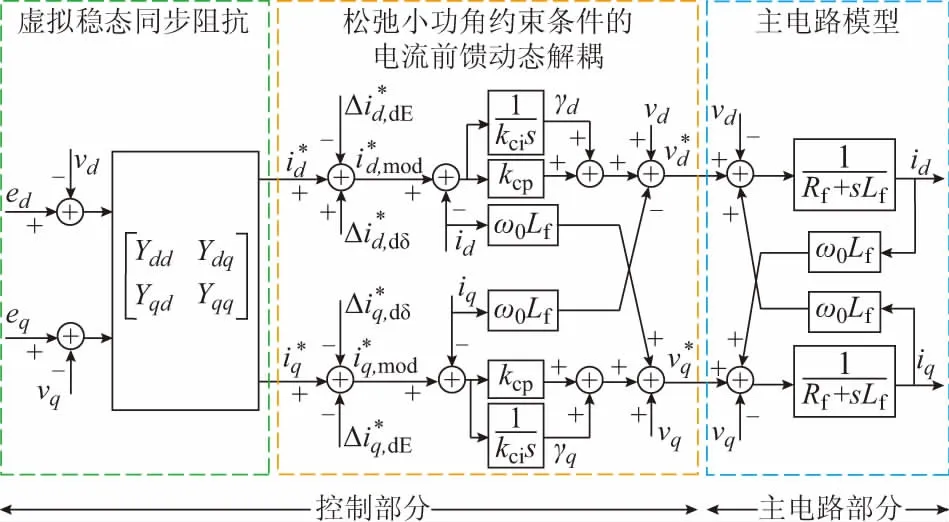
图3 松弛小功角约束条件的功率解耦策略控制框图Fig.3 Block diagram of control of power decoupling strategy relaxing small power angle condition
3.1 虚拟稳态同步输出阻抗
为了消除线路阻抗比R/X引起的功率耦合,采用如图3所示的虚拟稳态同步阻抗方案来改善VSG的输出阻抗特性。实现方法是在d-q坐标系下,将通过Q-E下垂产生VSG的虚拟内电势ed和eq与实际输出电压vd和vq的差值与虚拟稳态同步导纳矩阵相乘,得到电流指令。电流指令经过PI控制器后得到逆变器的控制信号。d-q坐标系按虚拟内电势E定向,因此ed=E,eq=0。
同步导纳矩阵可表示为:

(11)
式中:Lv为阻抗的电感;Rv为阻抗的电阻;ω0为d-q坐标系下的旋转角频率,此处选取电网额定频率。
为了验证虚拟稳态同步阻抗的有效性,推导VSG的等效输出阻抗模型。虚拟稳态同步阻抗部分方程如式(12)和式(13)所示。
(12)
(13)
电流环与主电路部分方程如式(14)和式(15)所示。
(14)
(15)
式中:kcp和kci分别为电流环PI调节器的比例系数和积分系数;Lf和Rf分别为滤波器的电感和电阻。
将式(14)和式(15)代入式(12)和式(13)中,可推导得出VSG实际的输出阻抗为:
(16)
式中:Gi=(kcps+kci)/[Lfs2+Rf+kcps+kci]。
从式(16)可以看出,对于直流分量,Gi|s=0=1。即对于d-q坐标系下直流分量的输出阻抗完全由设定的虚拟阻抗决定,与控制系统参数和输出滤波器的参数无关。因此,对应到实际三相静止坐标系中,说明工频信号的输出阻抗完全由设定的虚拟阻抗决定,避免了滤波器和控制环的影响,这大大简化了输出阻抗的设计。这在物理本质上是由于VSG控制策略通过控制虚拟内电势来控制功率的输出,而非逆变器端口电压,因此功率外环的稳态控制特性由虚拟内电势和虚拟阻抗决定。
根据式(16)可以画出采用虚拟稳态同步阻抗控制时逆变器的等效输出阻抗波特图,如图4中绿色点划线所示。由于存在对称性Zdd=Zqq,Zdq=-Zqd,因此这里只给出了Zdd和Zdq的波形。类似的,可以画出真实的物理阻抗和采用传统虚拟阻抗方法[19]的逆变器等效输出阻抗的波特图,其分别对应图中的红色虚线和蓝色实线。三种情况下电阻值均为3 Ω,电感均为25 mH(7.85 Ω)。值得注意的是,这组参数并非后文实验中所用参数。这里选取的参数同时包含了阻性和感性成分,目的是充分阐释输出阻抗在阻性和感性两个维度的特性,探究输出阻抗控制的一般规律,为塑造VSG输出阻抗以实现最优解耦性能提供参数选取的理论依据。
从图4中可以看出,在低频处,三条曲线完全重合,这表示虚拟同步稳态阻抗方案在工频处及其附近的低频段均能够较好地表现出所设定的输出阻抗特性,而不受控制系统和滤波器参数的影响。因此为了使VSG保证最优的解耦性能,可以直接通过设定Rv=0来实现纯感性输出阻抗。通过该方法塑造VSG输出阻抗十分简便,鲁棒性强。而在高频处,传统虚拟阻抗方案的Zdd比实际电感大,且相位超前真实电感90°;而虚拟稳态同步阻抗方案的Zdd比实际电感小且相位一致。这说明虚拟稳态同步阻抗方案降低了VSG在高频处的输出阻抗,当系统发生非线性负载或电网谐波扰动时,虚拟稳态同步阻抗上的谐波压降会更小,因此提高了VSG抗高频扰动的能力。同时,该方案通过电压和虚拟阻抗代数直接计算得到电流指令,而无需调节器,具有更快的调节性能。

图4 等效输出阻抗波特图Fig.4 Bode plots of equivalent output impedance
3.2 松弛小功角约束条件的电流前馈动态解耦
由3.1节可知,引入虚拟稳态同步阻抗策略可以使得VSG的输出阻抗由设定的虚拟同步阻抗决定,从而可以通过控制VSG的输出阻抗以解除由于线路阻抗比R/X引起的功率耦合。
此时,线路中功率传输方程简化为:
(17)
(18)
式中:X为VSG的等效输出感抗;E和V分别为VSG的虚拟内电势和VSG反馈的交流母线电压有效值。
根据式(9)得到此时耦合系数的表达式为:
Kc=sin2δ
(19)
进一步考虑消除功角引起的功率耦合,松弛VSG解耦控制的小功角约束条件。
为了方便阐释,将式(18)变换得到:
(20)
这在P-Q坐标系下构成一个二维功率圆,如附录A图A3所示。功率圆以(0,-V2/X)为圆心,以EV/X为半径。通常情况下,VSG作为一个发电机,其稳态运行点在第一象限。从图中可以看出,电压幅值变化的方向是在稳态工作点处的径向方向;而功角变化的方向是在稳态工作点处的切线方向。当功角或电压发生变化时,将会同时影响输出的有功功率和无功功率,即功率发生耦合。稳态工作点对应的功角越大,这种耦合作用越强烈,当且仅当功角为0°,即没有有功功率输出时,系统不存在耦合。
3.2.1无功功率动态解耦
如附录A图A4所示,当功角发生扰动时,在改变有功输出的同时由于Q-δ耦合使得无功输出发生了不期望的改变,因此偏离了期望的稳态工作点。因此,为了避免无功改变引起的误差,需相应改变VSG的虚拟内电势以抵消由功角扰动产生的无功变化。
由式(17)和式(18)可得此时在稳态工作点(E0,δ0)处的线性化小信号模型为:
(21)
令式(21)中ΔQ=0,即可以推出VSG虚拟内电势需要补偿的量为:
(22)
输出阻抗为感性时,VSG并网等效电路相量图如附录A图A5所示。根据相量图,电网电压的dq轴分量可以分别表示为:
(23)
输出电流的dq轴分量可以分别表示为:
(24)
(25)
其在稳态工作点(E0,δ0)处的小信号模型为:
(26)
(27)
有功和无功功率可由式(28)计算得出:
(28)
将其针对电流分量建立小信号模型为:
(29)
式中:Vd和Vq分别为输出电压在d-q坐标系下d轴和q轴的稳态分量。
由式(26)和式(27)可分别得到式(30)和式(31):
(30)
ΔE=-XΔiq-V(sinδ0)Δδ
(31)
将式(22)和式(30)代入式(31)中,得到
(32)
因此,无功解耦电流补偿指令的dq轴分量为:
(33)
3.2.2有功功率动态解耦
由式(21)可得在稳态工作点(E0,δ0)处,P-E耦合使得电压幅值扰动ΔE引起的有功偏差ΔP为:
(34)
设发生小扰动ΔE时,补偿P-E耦合引起的有功偏差的电流值为Δid和Δiq,则由式(29)和式(34)可得:

(35)
式中:Id和Iq分别为输出电流在d-q坐标系下d轴和q轴的稳态分量。
因此可得P-E解耦电流补偿指令为:
(36)
为了便于获得P-E解耦电流补偿指令,电压稳态值E0可由电压参考值Eref代替。
综上,根据式(33)和式(36)可以得到,加入无功和有功解耦电流补偿后的电流环指令为:
(37)
(38)

从式(37)和式(38)中可以看出,前馈补偿量的计算只需要检测电压、电流、功角等实时运行状态,而无需依赖难以实时测量或存在漂移的线路阻抗等参数,因此理论上该方案能实现功率的精确解耦并具有较好的参数鲁棒性。
4 稳定性和功率耦合特性分析
4.1 状态空间全局小信号模型
为了研究引入所提的松弛小功角约束条件解耦方案对VSG特性的影响,建立了改进前后的VSG状态空间全局小信号模型。主要参数见附录A表A1。
线性化后的状态空间小信号模型可以用式(39)和式(40)表示。
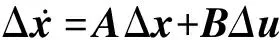
(39)
Δy=CΔx+DΔu
(40)
Δx=ΔωΔδΔidΔiqΔγdΔγqΔQfT
(41)
Δu=ΔPrefΔQrefΔωrefΔErefΔωgΔvgT
(42)

(43)
式中:A,B,C,D分别为状态矩阵、输入矩阵、输出矩阵和前馈矩阵;Δx,Δu,Δy分别为状态变量、输入向量和输出向量;Δγd和Δγq分别为电流环d轴和q轴PI调节器的积分器输出变化量;ΔQf为采样滤波后的无功功率变化量;Δωg和Δvg分别为交流母线的频率和电压变化量。
该模型以有功功率和无功功率作为输出变量,可以用来分析VSG的功率动态响应特性。传递函数矩阵G(s)的表达式为:
G(s)=C(sI-A)-1B+D
(44)
其中G(s)中的G11(s)和G22(s)两个元素分别对应VSG的有功控制环和无功控制环的传递函数ΔP(s)/ΔPref(s)和ΔQ(s)/ΔQref(s),分别描述了有功功率控制环和无功功率控制环的响应特性。VSG的功率耦合作用可用ΔQ(s)/ΔPref(s)和ΔP(s)/ΔQref(s)两个传递函数描述,分别对应G(s)中的G21(s)和G12(s)两个元素,其涵义分别是有功指令变化时输出无功功率的响应以及无功指令变化时输出有功功率的响应。
4.2 参数根轨迹和稳定性分析
附录A图A6分别给出了采用基于小功角近似的传统虚拟阻抗解耦方法以及本文提出的松弛小功角约束条件后的改进解耦方法时,VSG系统状态矩阵的特征根随转动惯量和阻尼系数增加时的轨迹图。
从图A6中可以看出,当采用相同的控制参数时,引入本文提出的解耦方法后,使得欠阻尼区域内的特征根在复平面的位置向实轴近似垂直移动,并同时略向远离虚轴的方向微微移动,系统的阻尼比也相应增加。这表明所提出的解耦方法与传统虚拟阻抗方法相比,更进一步减弱了原有系统的功率耦合对系统振荡的放大作用。因此,改进后VSG的性能也更符合有功功率控制环自身参数设计所期望的动态性能。
为了进一步对比分析系统的稳定性,附录A图A7给出了系统有功控制环路在选取不同转动惯量和阻尼系数下的系统增益裕度和相位裕度变化曲线。从两种方案的对比可以明显地看出,相比传统解耦方案,本文提出的方案增加了系统的增益裕度和相位裕度,因此更进一步增强了系统的稳定性。
4.3传统与改进VSG方案的功率耦合特性对比分析
首先分析有功功率环扰动对无功功率环的耦合作用。图5(a)给出了不加任何解耦控制、采用传统虚拟阻抗方法以及采用本文提出的解耦策略时传递函数ΔQ(s)/ΔPref(s)的波特图。ΔQ(s)/ΔPref(s)表征了有功功率控制环对无功功率的耦合影响,其增益越大,表示耦合作用越强。

图5 ΔQ(s)/ΔPref(s)和ΔP(s)/ΔQref(s)的波特图Fig.5 Bode plots of ΔQ(s)/ΔPref(s) and ΔP(s)/ΔQref(s)
从图5(a)中可以看出,当不加任何解耦控制时,ΔQ(s)/ΔPref(s)的低频和中频增益都最大,表示无功功率的动态响应受有功功率环耦合的影响最大。而且,其稳态增益不为零(-12.5 dB),表示由于耦合作用使得有功功率扰动会引起无功功率输出的稳态误差。幅频曲线在1.05 Hz处存在一个谐振峰(-5.84 dB),说明有功功率指令扰动会引发无功功率的振荡。低频段相位为180°,这表明低频段无功功率的变化方向与输入有功功率指令的变化方向相反。当引入传统的虚拟阻抗方法后,使ΔQ(s)/ΔPref(s)的稳态增益和谐振峰幅值均有所下降(分别为-19.5 dB和-12.7 dB),这减弱了因功率环间的耦合作用而引起的振荡和稳态误差。而采用本文提出的松弛小功角约束条件的解耦策略后,可以进一步减小ΔQ(s)/ΔPref(s)的稳态增益和谐振峰的幅值(分别为-37.3 dB和-30.9 dB),因此可以更加有效地解除功率环间的耦合。
同理分析无功功率环扰动对有功功率环的耦合作用。图5(b)分别给出了不加任何解耦控制、采用传统虚拟阻抗方法以及采用本文提出的解耦策略时传递函数ΔP(s)/ΔQref(s)的波特图。
从图中可以看出,与无功耦合不同的是,幅频曲线在低频段呈现出衰减特性(对应的稳态增益为0,即|G(0)|=0)。这表明无功的变化不会对输出有功功率的稳态值产生影响,功率耦合不会使有功功率产生稳态误差。这是由于有功功率环中存在积分器,输出有功功率通过积分补偿使得有功稳态时也能够实现对有功指令的无差跟踪。但在其他频率的增益仍然存在,且在1.15 Hz处存在谐振峰,这说明动态过程中无功功率控制会对有功功率起到耦合影响,且会引发有功功率振荡。对比三种控制策略的幅频曲线在各频率点处的增益和谐振峰幅值(不加解耦控制、传统虚拟阻抗和本文所提方法对应的谐振峰幅值分别为-8.93,-15.5,-25.1 dB),可以看出本文提出的松弛小功角约束条件的解耦策略与传统的虚拟阻抗解耦方法相比,可以更好地消除由于有功耦合而对输出有功功率的影响,实现了更好的解耦作用。
5 实验验证
为验证所提功率解耦方法的有效性,搭建了实验平台,主要参数见附录A表A1。控制算法通过数字信号处理器(DSP)TMS2812 芯片实现。图6分别给出了不加任何解耦控制、采用传统虚拟阻抗方法以及采用本文提出的松弛小功角约束条件解耦策略时VSG输出有功功率和无功功率的动态响应波形。
在t<2 s 时,VSG运行在稳态,输出有功功率为0 W,无功功率为1 000 var。在t=2 s 时,有功指令从0阶跃到1 000 W。从有功功率波形可以看出,系统运行在欠阻尼状态,振荡较剧烈。与从三种控制策略下的有功响应波形可以看出,采用本文提出的解耦方法之后,系统的阻尼比略增加,振荡稍降低,这与前面的根轨迹分析结果相一致。而从t=2 s时的无功响应波形可以明显地看出不同策略下有功功率控制对无功环耦合的影响,具体的无功响应性能指标见表1。
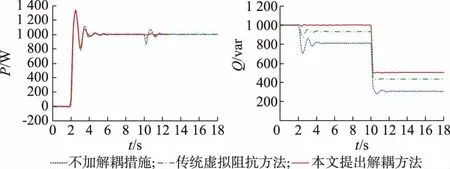
图6 有功功率和无功功率动态响应实验波形Fig.6 Experimental waveforms of dynamic response of active power and reactive power

控制策略无功功率响应性能指标(有功阶跃扰动)有功功率响应性能指标(无功阶跃扰动)动态最大偏差/var调节时间/s稳态偏差/var动态最大偏差/W调节时间/s稳态偏差/W不加解耦措施2973.41891402.50传统虚拟阻抗1313.466542.50本文提出方法101.7061.50
当按照不加解耦措施的基本VSG控制算法进行功率控制时,由于线路阻抗比较高(R/X=0.25),且此时功角为0.138 rad(7.9°),有功功率环和无功功率环之间的耦合严重,无功功率跟随有功功率的响应也发生了剧烈的振荡,动态过程中最大偏差为297 var(29.7%),调节时间约为3.4 s。同时,当达到新的稳态时,无功功率受有功输出的影响降低到811 var,产生了189 var的稳态误差,误差率为18.9%。当加入传统的虚拟阻抗策略时,功率耦合得到了明显的减弱,但由于此时稳态功角为0.176 2 rad(10.1°),小功角近似误差引起的功率耦合依然存在,因此有功阶跃对无功功率的影响依然明显。此时,无功功率的振荡频率变化不大,动态最大偏差为131 var(13.1%),调节时间仍为3.4 s,稳态输出为934 var,对应的稳态误差为66 var,误差率为6.6%。而当引入本文提出的解耦方法时,无功功率耦合得到了更好的改善。此时,无功功率响应动态过程中的最大偏差量为10 var(1%),调节时间降为1.7 s,因此很好地改善了无功功率的动态响应。达到稳态时,无功功率的偏差为0,说明本文提出的方法消除了功率耦合引起的无功稳态误差,使VSG可以按照无功环自身控制的要求输出,而不再受有功控制环的影响。
在t=10 s 时,通过调节无功功率指令,分别使得三种控制策略下VSG输出的无功功率均发生500 var的阶跃下降。在此种条件下,观察不同控制策略下VSG的有功功率和无功功率动态响应。首先,从无功功率本身的动态响应可以看出,当不加入解耦措施时,无功阶跃响应存在一个动态振荡的过程,这与无功功率控制环自身所设计的动态特性不符,这是由于功率环之间的耦合将有功环的振荡特性引入了无功环内。当加入虚拟阻抗控制策略后,动态振荡得到减弱,能更快地达到稳态,但依然存在超调。当加入本文提出的解耦方法后,无功响应的动态振荡和超调消失,很好地改善了无功功率的动态响应性能。
然后,从有功功率的响应波形可以看出不同策略下无功功率控制对有功环耦合的影响,具体的有功响应性能指标见表1。当按照不加解耦措施的基本VSG控制算法进行功率控制时,无功功率控制对有功功率输出的耦合影响较为严重,有功功率由于无功环的扰动产生了振荡过程,动态过程中最大偏差为140 W(14%),调节时间约2.5 s。由于有功功率控制环路的积分特性,耦合不会引起有功功率的稳态偏差。当加入传统的虚拟阻抗策略时,有功功率的耦合得到减弱。动态过程中最大偏差减小至54 W(5.4%),调节时间约为2.5 s。而当引入本文提出的解耦方法时,有功功率耦合得到了进一步的减弱。此时,动态过程中有功最大偏差仅为6 W(0.6%),同时调节时间降为1.5 s,因此有功功率的动态响应得到了很突出的改善。
6 结语
VSG的功率耦合问题会影响其输出功率的控制精度、动态响应以及系统稳定性。本文在对VSG的功率耦合问题分析的基础上,提出了一种可松弛小功角约束条件的功率解耦方案,阐释了其基本原理和实现方法。然后,建立了改进VSG控制策略的状态空间全局小信号模型,通过与传统解耦策略进行对比分析,论证了提出的解耦方法可以更有效地减弱有功环与无功环之间的耦合作用,同时可以增加系统的增益和相位裕度,增强VSG系统的稳定性。最后,搭建了实验平台,实验结果表明所提方法可以有效消除由于功率耦合产生的静态误差以及功率振荡,提高VSG有功功率和无功功率的动静态响应性能。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] 王成山,王守相.分布式发电供能系统若干问题研究[J].电力系统自动化,2008,32(20):1-4.
WANG Chengshan, WANG Shouxiang. Study on some key problems related to distributed generation systems[J]. Automation of Electric Power Systems, 2008, 32(20): 1-4.
[2] 帅智康,邹福筱,涂春鸣,等.微网暂态稳定性研究[J].电力系统自动化,2015,39(16):151-159.DOI:10.7500/AEPS20141118002.
SHUAI Zhikang, ZOU Fuxiao, TU Chunming, et al. Review on transient stability of microgrid[J]. Automation of Electric Power Systems, 2015, 39(16): 151-159. DOI: 10.7500/AEPS20141118002.
[3] 曾正,赵荣祥,汤胜清,等.可再生能源分散接入用先进并网逆变器研究综述[J].中国电机工程学报,2013,33(24):1-12.
ZENG Zheng, ZHAO Rongxiang, TANG Shengqing, et al. An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J]. Proceedings of the CSEE, 2013, 33(24): 1-12.
[4] 全锐,潘文霞.考虑惯性动能的风电场旋转备用容量优化方法[J].电力系统自动化,2015,39(24):23-28.DOI:10.7500/AEPS20150130009.
QUAN Rui, PAN Wenxia. Optimization of wind farm spinning reserve capacity considering rotor inertia kinetic energy[J]. Automation of Electric Power Systems, 2015, 39(24): 23-28. DOI: 10.7500/AEPS20150130009.
[5] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[6] BECK H P, HESSE R. Virtual synchronous machine[C]// 9th International Conference on Electrical Power Quality and Utilisation, October 9-11, 2007, Barcelona, Spain.
[7] GAO F, IRAVANI M R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 850-859.
[8] SALVATORE D, JON A S, OLAV B F. A virtual synchronous machine implementation for distributed control of power converters in SmartGrids[J]. Electric Power Systems Research, 2015, 122: 180-197.
[9] ALATRASH H, MENSAH A, MARK E, et al. Generator emulation controls for photovoltaic inverters [J]. IEEE Transactions on Smart Grid, 2012, 3(2): 996-1011.
[10] 张兴,朱德斌,徐海珍.分布式发电中的虚拟同步发电机技术[J].电源学报,2012,10(3):1-6.
ZHANG Xing, ZHU Debin, XU Haizhen. Review of virtual synchronous generator technology in distributed generation[J]. Journal of Power Supply, 2012, 10(3): 1-6.
[11] LIU J, MIURA Y, ISE T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J]. IEEE Transactions on Power Electronics, 2015, 31(5): 3600-3611.
[12] 吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34(16):2591-2603.
LÜ Zhipeng, SHENG Wanxing, ZHONG Qingchang, et al. Virtual synchronous generator and its applications in micro-grid[J]. Proceedings of the CSEE, 2014, 34(16): 2591-2603.
[13] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150508006.
ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150508006.
[14] 李鹏,杨世旺,王阳,等.基于相对增益分析的目标函数对角化微网功率解耦控制方法[J].中国电机工程学报,2014,34(13):2039-2046.
LI Peng, YANG Shiwang, WANG Yang, et al. Objective function diagonalization decoupling control of microgrid power based on relative gain analysis[J]. Proceedings of the CSEE, 2014, 34(13): 2039-2046.
[15] 张也,颜湘武.微网功率耦合特性分析及解耦控制[J].电网技术,2016,40(3):812-818.
ZHANG Ye, YAN Xiangwu. Coupling analysis and decoupling control of microgrid power[J]. Power System Technology, 2016, 40(3): 812-818.
[16] CHANDORKAR M C, DIVAN D M, ADAPA R. Control of parallel connected inverters in standalone AC supply systems[J]. IEEE Transactions on Industry Applications, 1993, 29(1): 136-143.
[17] 杜威,姜齐荣,陈蛟瑞.微电网电源的虚拟惯性频率控制策略[J].电力系统自动化,2011,35(23):26-31.
DU Wei, JIANG Qirong, CHEN Jiaorui. Frequency control strategy of distributed generations based on virtual inertia in a microgrid[J]. Automation of Electric Power Systems, 2011, 35(23): 26-31.
[18] SHINTAI T, MIURA Y, ISE T. Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676.
[19] GUERRERO J M, GARCIA D V L, MATAS J, et al. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control[J]. IEEE Transactions on Industrial Electronics, 2005, 52(4): 1126-1135.
[20] KAREL D B, BRUNO B, JEROEN V K, et al. A voltage and frequency droop control method for Parallel inverters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1107-1115.
[21] LI Y, LI Y W. Power management of inverter interfaced autonomous microgrid based on virtual frequency-voltage frame[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 30-40.
[22] 李武华,王金华,杨贺雅,等.虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J].中国电机工程学报,2017,37(2):381-391.
LI Wuhua, WANG Jinhua, YANG Heya, et al. Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J]. Proceedings of the CSEE, 2017, 37(2): 381-391.
[23] BIN L, LIN Z, XIRUI Y, et al. Improved power decoupling control strategy based on virtual synchronous generator[J]. IET Power Electronics, 2017(10): 462-470.
[24] BRISTOL E. On a new measure of interaction for multivariable process control[J]. IEEE Transactions on Automatic Control, 1966, 11(1): 133-134.
李明烜(1990—),男,博士研究生,主要研究方向:新能源发电与并网。E-mail: lmx2027@stu.xjtu.edu.cn
王 跃(1972—),男,通信作者,博士,教授,博士生导师,主要研究方向:大功率电能变换。E-mail: davidwangyue@mail.xjtu.edu.cn
徐宁一(1991—),男,硕士研究生,主要研究方向:新能源发电与并网。E-mail: ning1xu@163.com

