级联型储能系统中虚拟同步发电机控制及电池自均衡策略

李 新, 杨苒晨, 邵雨亭, 胡耀威, 陈国柱

(浙江大学电气工程学院, 浙江省杭州市 310027)

0 引言

近年来,风电等可再生能源装机容量、电压等级不断上升,而其间歇性和不确定性特点以及区域电网消纳有限等问题造成了广泛的“弃风弃光”现象[1],同时给电力系统调度和优化运行带来挑战[2-3]。

电池储能系统(battery energy storage system,BESS)成为解决上述问题的有效途径之一[4]。受电池特性及传统两电平或三电平拓扑耐压影响,现有BESS电压等级、系统容量较低,难以适应大规模可再生能源系统的功率波动、维持微电网稳定等。而级联H桥变流器的模块化特点可实现单机系统高压、大容量化,成为大规模储能发展方向[5]。

传统的储能系统控制方法响应快、控制灵活,但同时具有低阻尼、低惯性的不足。随着新能源对电网渗透率不断提高,电网转动惯量降低,使得电力系统频率稳定性、运行安全性逐渐降低[6-7]。为此,学者提出虚拟同步发电机(virtual synchronous generator,VSG)的控制方法[8-9],通过引入虚拟惯量提高系统的阻尼,增强电网稳定性[8],而级联H桥变流器阻抗小、调节快速、灵活,因此VSG控制的建模分析及参数整定对系统稳定性至关重要。文献[10-11] 通过建立VSG有功环路传递函数分析了虚拟惯性和阻尼系数与控制性能的关系,但未对VSG无功功率—电压调节特性进行分析。文献[12]建立了VSG控制的工频小信号模型,给出了参数快速设计方法,但并未考虑交流侧阻抗特性对模型完整性及控制分析的影响。

此外,受电池特性差异及外部环境影响,子模块电池荷电状态(SOC)存在不平衡现象,进而造成电池的过充、过放,影响系统寿命[13]。对此,文献[14]利用载波层叠调制方式实现了相内电池模组SOC的均衡,子模块较多时,该方法所需要载波较多,软、硬件资源占用较大。文献[15]提出差异化充放电方法,在不均衡时进行选择谐波消除脉宽调制(SHE-PWM),通过不同导通时间实现各子模块输出功率不同,实现SOC一致,该方法需要两种调制方式,占用资源较大且未考虑两种调制方法切换对BESS的影响。

针对上述VSG模型的不足,本文在详细分析同步发电机二阶等效模型基础上,建立反映并网交流侧阻抗特性的宽频带小信号动态模型,分析交流侧阻抗特性给VSG控制稳定性带来的潜在影响,提高了模型分析准确度。通过建立具有一次调频、调压特性的VSG频域模型分析了主要参数对有功和无功控制及VSG系统稳定性的影响关系,并利用根轨迹法对相关参数进行设计。同时针对级联型储能系统电池存在的SOC不均衡问题,给出一种基于改进型最近电平调制 (I-NLM) 方法的SOC均衡方法。最后通过搭建仿真模型,验证了建立的VSG模型及控制参数对BESS特性影响分析的正确性以及所提SOC均衡调制方法的有效性。

1 级联H桥拓扑及VSG控制策略

1.1 级联H桥拓扑及BESS控制结构

基于级联H桥拓扑的大规模储能系统结构参见附录A图A1,每相N个H桥子模块,L1和C1分别为直流侧滤波电感和滤波电容;Vdc为H桥直流侧额定电压;Za,Zb,Zc为交流侧阻抗。附录A图A2为基于级联H桥拓扑的VSG控制结构及等效示意图。图中:ei,ui,ugi分别为VSG虚拟电动势、输出电压和电网电压,其中i取a,b,c;ii为输出电流;δ为VSG虚拟功角;Lf和Lg分别为输出滤波电感和并网线路电感;Rf和Rg分别为滤波电感电阻和线路电阻;Cf滤波电容,文中忽略其影响;X=ωL为交流测线路总感抗(L=Lf+Lg),总电阻为R=Rf+Rg。

1.2 VSG数学模型

根据牛顿第二定律,在极对数p=1时,同步发电机机械特性表达式为:

(1)

(2)

式中:Pm,Pe,PD为对应功率的归一化值;ωN为额定频率;ω*为VSG输出频率的归一化值;Δδ为功角变化量;Tj为衡量不同功率、容量等级同步发电机惯性的时间常数;J为同步发电机转子转动惯量;SB为容量归一化基准值。

考虑到系统频率波动很小,近似认为ω*≈1,结合功角变化量Δδ与频率偏差Δω的关系,得出反映同步发电机转子机械特性的VSG转子模型表达式为:

(3)

其次,由附录A图A2所示控制结构及原理图可得到反映同步发电机电磁特性的VSG电磁模型表达式为:

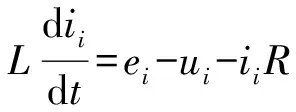
(4)

式中:下标i取a,b,c。

当VSG所接入电网为无穷大电网时,根据附录A图A3所示矢量图得出VSG输出功率表达式分别为:

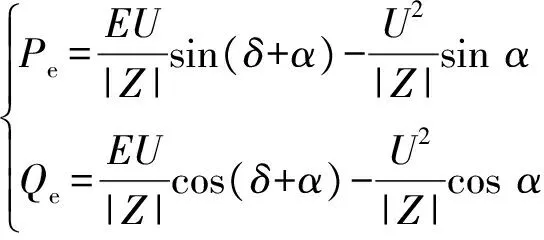
(5)

式中:α=arctan(R/X)为VSG交流侧阻抗角;E为VSG虚拟电动势;U为电网电压;Z为交流侧阻抗。

1.3 VSG控制策略

根据VSG数学模型搭建的大规模储能系统控制策略如图1所示。图中:Pref和Qref分别为BESS有功功率和无功功率的指令参考值;uiref为VSG控制输出参考信号,其中i取a,b,c;UN为电网额定电压;fN为电网额定频率;D为阻尼系数。

图1 级联型储能系统VSG控制框图Fig.1 Block diagram of control of VSG for cascaded energy storage system

图1所示VSG控制框图主要包括4个部分:一次频率调节部分、VSG虚拟转子运动部分、一次电压调节部分和虚拟自动励磁调节部分。其中,对于储能系统的一次调频、调压特性,依国标[16-17]规定:20 kV以下三相供电电压偏差为标称电压的±7%;频率偏差为±0.5 Hz;结合同步发电机的调频、调压特性,本文中储能电站虚拟同步机的一次调频和一次调压系数按依照如下规则整定。

当系统频率波动5%额定频率时,储能系统输出有功波动100%额定有功功率,即

(6)

式中:ΔP和PN分别为BESS有功波动量和额定有功功率;kf为VSG控制的一次调频系数。

当系统电压波动15%额定电压时,储能系统输出无功波动100%额定无功功率,即

(7)

式中:ΔQ和QN分别为BESS的无功波动量和额定无功功率;ΔU为电网电压波动量;ku为VSG控制的一次调压系数。

2 VSG宽频带小信号动态模型及参数分析

2.1 宽频带小信号动态模型

分析VSG参数对储能系统稳定性及动态特性的影响,根据VSG数学模型建立宽频带小信号动态模型。

参照附录A图A3,以电网电压U∠0°为d轴参考,建立d-q旋转坐标系,VSG虚拟电动势为E∠δ,在此坐标系下,式(4)所述VSG电磁方程可表示为:

(8)

(9)

代入X=ωL,求得d-q坐标系下的电流表达式为:

(10)

近似忽略交流侧阻抗的功率损耗,根据瞬时无功功率理论计算d-q坐标系下VSG输出电磁功率为:

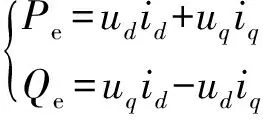
(11)

将式(9)和式(10)代入式(11),得到电磁功率频域表达式为:

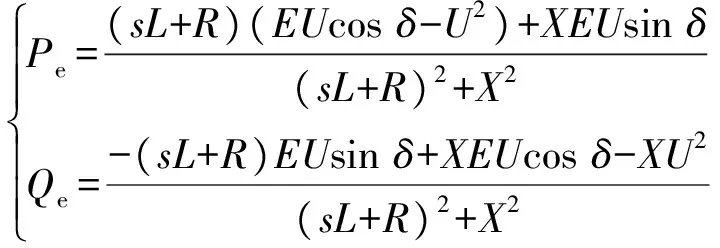
(12)

对比式(5)和式(12)可以看出,式(5)中的功率表达式即为式(12)在系统稳态时的情况。考虑虚拟电动势E和功角δ摄动对功率的影响,将E=E0+ΔE和δ=δ0+Δδ代入式(12)得到:

(13)

(14)

式中:E0和δ0分别为稳态时VSG的虚拟电动势和功角。

由式(14)可知,VSG功率关系矩阵存在一对共轭极点s1,2,且其位置由R和L决定,当R≪L时,共轭极点靠近虚轴,即VSG模型在ω处存在谐振,因此VSG模型需要考虑此部分。HPδ(s)和HQE波特图参见附录A图A4。工况为Pe=0.8(标幺值),Qe=0.3(标幺值),E=1.02(标幺值),U=1.0(标幺值),X=0.047(标幺值),R=0.008(标幺值)。

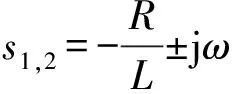
(15)

其次,式(14)表明VSG输出的有功功率和无功功率通过电压和功角存在耦合,且文献[17-18]指出耦合作用可降低VSG稳定性、促进功率振荡,为分析宽频带下的功率耦合特性及主要影响因子,引入耦合度系数。其中,定义有功功率Pe对电势E的偏导HPE(s)与有功功率Pe对功角δ的偏导HPδ(s)的比值为无功控制对有功控制的耦合度系数Kc,P,即

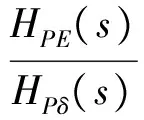
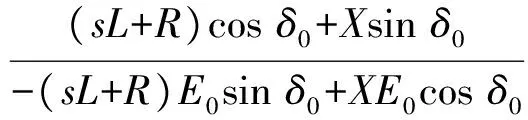
(16)

定义无功功率Qe对电势δ的偏导HQδ(s)与无功功率Qe对电势E的偏导HPE(s)的比值为有功控制对无功控制的耦合度系数Kc,Q,即

(17)

对比式(16)和式(17),在近似E0≈1时,有功和无功环路的耦合系数特性幅频特性相同而相频特性相差180°,参见附录A图A5所示耦合度系数的波特图。 稳态时,功率耦合度系数K可统一为:

(18)

根据式(18),附录A图A6给出了稳态时耦合度系数K与BESS交流测阻抗特性的关系。可以看出,交流侧R越大,X越小,功率控制的耦合度系数K越大,耦合作用对VSG稳定性影响愈大,且此时稳态功率存在控制误差。对中高压、大容量BESS,由于交流侧阻抗特性R/X较小,功率耦合关系可近似忽略。

2.2 VSG参数及稳定性分析

根据VSG宽频带小信号模型以及图1所示BESS控制框图,在不考虑功率耦合时,独立分析功率控制特性并近似E≈U。附录A图A7(a)和图A7(b)分别给出了VSG有功功率和无功控制的小信号控制环路。

根据图A7,有功和无功控制的开环传递函数表达式分别为:

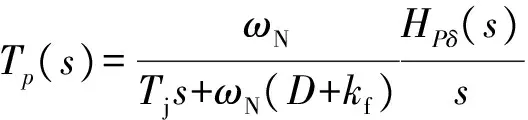
(19)

(20)

令Dp=D+kf为考虑VSG一次调频和阻尼特性的综合频率系数,GPI(s)为比例—积分(PI)调节传递函数,其比例系数和积分系数分别为kp和ki。

分析VSG中虚拟惯性时间常数Tj和综合频率系数Dp与控制稳定性的关系,由式(19)得出VSG有功控制环路的闭环特征方程为:

as4+bs3+cs2+ds+e=0

(21)

式中:

综合考虑Tj和Dp对VSG有功环路控制动态特性及稳定性的影响,给出当Tj取不同数值且Dp增大时的参数根轨迹簇,如图2(a)所示。从图2(a)可以看出,Dp为0时,闭环特征根位于虚轴左侧,系统失稳;且Dp一定时,随着Tj增大,有功控制阻尼减小,超调量增加;而在Tj一定时,随着Dp增大,控制系统阻尼增加,动态响应速度变慢。VSG有功控制参数Tj和Dp可根据图2(a)及BESS性能要求合理整定。

图2 不同控制参数下的VSG功率环路参数根轨迹簇Fig.2 Parameter root loci of active control loop for VSG with different control parameters

对于无功控制环路,根据式(20)所示无功开环传递函数得出无功闭环特征方程,展开并等效处理后得出关于参数ki根轨迹方程为:

(22)

式中:

进一步分析无功控制环路PI调节参数对控制稳定性的影响。给定不同的kp,通过根轨迹图观察ki的影响,如图2(b)所示。

从图2(b)可以看出:根据VSG宽频带小信号动态模型建立的无功控制环路,存在一个位于原点处的特征根;当系数kp较小时,随着系数ki增加,无功控制环路的闭环特征根逐渐靠近虚轴并最终进入右半平面,进一步增大ki,特征根趋于左半平面的零点,且当kp>0.36时,全部特征根均位于左半平面;在ki一定时,系统初始特征根逐渐靠近零点,无功控制动态响应速度变慢;当kp和ki均较大时,特征根与零点构成两对偶极子,无功调节性能降低。

3 电池SOC均衡调制

对于级联型BESS,由于运行工况、电池老化等导致的参数不一致性影响,存在相内子模块电池SOC不均衡的问题,而VSG无法直接实现电池SOC的均衡,文献[19]在调制波上叠加SOC偏差信号的方法控制模块输出功率,达到了电池模组间的均衡。但叠加的电池SOC偏差信号容易使输出电压存在畸变。为此,本文在VSG控制基础上,结合文献[20],利用I-NLM方法在级联H桥变流器调制过程中完成子模块SOC的自均衡,且不会引起调制波畸变。

最近电平调制(NLM)是一种利用最近电平瞬时逼近调制波的调制方法,常应用于多电平变流器子模块均压处理。实现过程中对子模块电压进行排序并根据约定条件投入其中的n个子模块,子模块数n表达式为:

(23)

最近电平调制方法实现简单,但在子模块数量较少时,最近电平调制对调制波逼近效果较差,变流器输出电压波形存在较大畸变。为此,本文采用I-NLM方法作为VSG控制的输出调制。 子模块电池SOC进行降序排序,并计算各模块电池SOC与相内电池SOC平均值的偏差ΔSSOC且偏差最大值与最小值分别为ΔSSOC,max(>0)和ΔSSOC,min(<0),根据式(23)确定投入数目,具体均衡调制原则如下。

1)处于放电,若SOC最小偏差绝对值|ΔSSOC,min|未超过设定均衡阈值SSOC,th,则依次投入SOC降序中的前n个子模块且输出电压极性与uref极性一致,利用第n+1个子模块进行脉宽调制;反之,投入SOC降序中的前n+1个子模块且输出电压极性与uref极性一致,同时反极性投入ΔSSOC,max对应模块进行充电,利用第n+2个子模块进行脉宽调制。

2)处于充电,若SOC最大偏差ΔSSOC,max未超过设定均衡阈值SSOC,th,依次投入SOC降序中的后n个子模块且输出电压极性与uref极性一致, 利用第N-n个子模块进行脉宽调制;反之,投入SOC降序中的后n+1个子模块且输出电压极性与uref极性一致,同时反极性投入ΔSSOC,min对应模块进行放电,利用第N-n-1个子模块进行脉宽调制。

经过上述调制,BESS相内模块电池SOC将迅速趋于一致。由于电池SOC在短时间(数个基波周期)内变化很小,为优化计算时间,根据设定的 SOC不均衡度阈值进行定时排序。具体流程图可参见附录A图A8。

图3(a)和图3(b)分别给出了调制过程中最近电平调制和脉宽调制的示意图。图中:uNLM为最近电平调制下BESS输出电压；uI-NLM和ueq分别为I-NLM下实际输出电压和等效电压;Ts为控制器计算周期;t1和t2分别为计算周期Ts内低电平和高电平作用时间;Vn为投入n个H桥模块时的输出电压;us为第s个控制周期参考电压信号采样值。

图3 最近电平调制及I-NLM关系示意图Fig.3 Relationship schematic diagram of NLM and I-NLM method

根据图3(b)所示I-NLM示意图, 脉宽调制子模块的低、高电平输出作用时间t1和t2满足:

Vn+1t2+Vnt1=usTs

(24)

结合t1+t2=Ts可计算出,第s个控制周期Ts时间内,时间图t1和t2分别为:

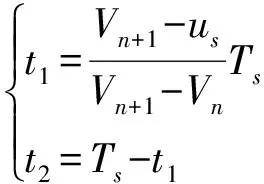
(25)

从式(23)和式(25)可以看出,I-NLM为最近电平调制和脉宽调制的结合。同时,在保证等效输出波形ueq情况下,根据图3(b)所示I-NLM示意图,将相邻控制周期内的高、低电平进行组合,从而进一步降低BESS开关损耗。

根据图3(c)所示两种调制方法的对比波形可知,I-NLM方法由于具有脉宽调制特点,输出电压波形更逼近调制波,总谐波畸变率较传统最近电平调制更小。当系统模块数较多时,可在降低谐波含量的同时,通过降低脉宽调制子模块开关频率,进一步提高BESS效率。

4 仿真分析

为了验证上述理论分析及I-NLM方法的正确性,利用Simulink/MATLAB搭建10 kV/10 MW的级联H桥型BESS仿真模型,每相H桥子模块数N=14。模型具体参数见附录B表B1。

4.1 仿真算例1

图4(a)和图4(b)分别给出了BESS在不同的VSG控制参数下,有功功率变化的动态响应结果。其中,图4(a)中选定综合频率系数Dp=0.1,分别选取不同的虚拟惯性时间常数Tj。可以看出,随着Tj增大,有功动态响应超调量增加,但Tj较小时,动态响应较快,系统惯量较小,同步发电机特性不明显。图4(b)中选定Tj=2.5 s,随着Dp增大,有功控制超调量减小,系统稳定性增强,验证了2.2节VSG宽频带频域模型中主要参数分析的正确性。

图4 BESS输出功率动态仿真波形Fig.4 Dynamic simulation waveforms of output power for BESS

结合上述不同VSG控制参数下动态仿真结果以及2.2节根轨迹分析,考虑功率器件较小的耐受过冲能力,选取Tj=3.5 s,Dp=0.45(即阻尼系数D=0.386),无功控制参数kp=0.01,ki=1.6,BESS的功率响应特性如图4(c)所示,有功指令分别在1 s和3 s时跳变至0.8(标幺值)和0.6。

由图4(c)可以看出:有功指令跳变时功率无超调量且调节时间短(<0.5 s);同时由于功率耦合关系,有功功率跳变时,无功功率出现很小范围的波动,由于R/X较小,耦合作用较弱,稳态时误差仍为0,说明了VSG控制参数分析及功率耦合关系的正确性。

4.2 仿真算例2

BESS运行过程中的输出电压、电流波形参见附录A图A9。可以看出,I-NLM下BESS输出电压波形为多电平且输出电流波形良好,畸变很小。

进一步分析I-NLM方法对电池模组SOC均衡的作用,子模块电池分别设置不同初始SOC值,给定BESS无功指令为0,初始有功指令为0.8,系统放电;4 s时跳变至-0.4,系统充电;8 s时跳变至0.8,系统放电;12 s时跳变至-0.4,系统充电。BESS功率变化波形以及电池模组SOC均衡过程分别如图5(a)和图5(b)所示。

图5 BESS输出功率及子模块电池SOC均衡变化波形Fig.5 Waveforms of output power for BESS and SOC balancing for sub-module batteries

从图5可以看出:在采用的I-NLM情况下,BESS充电、放电过程中,SOC较高的模块,放电速率较大而充电速率较小;SOC较低的模块,放电速率较小而充电速率较大。最终,相内各子模块电池SOC不断收敛,趋于一致,实现均衡。

5 结语

为保证BESS的稳定性和动态性能,VSG控制参数设计非常关键,本文在建立的宽频带VSG模型基础上详细分析了主要控制参数对系统性能的影响,并给出了参数优化、整定方法。同时利用I-NLM方法实现了BESS相内电池间SOC的均衡处理,本文主要结论如下。

1)建立反映并网交流侧阻抗特性的宽频带小信号动态模型,给出VSG电磁功率与虚拟电势E及功角δ的关系,表明VSG功率关系矩阵存在一对接近虚轴的共轭极点,降低控制稳定性;分析了阻抗特性对功率控制的耦合度系数的影响,指出R越大,X越小,耦合度系数K越大,稳态功率存在控制误差。并利用VSG频域模型和参数根轨迹簇分析法指出主要控制参数对VSG稳定性的影响,其中参数Tj和Dp决定有功控制的稳定性和动态性能,参数kp和ki影响了无功调节性能。为中高压等级BESS中VSG控制参数整定的可靠性以及控制稳定性提供了依据。

2)级联型BESS存在SOC均衡问题,所提出的I-NLM方法可在BESS运行过程中利用级联H桥变流器调制实现子模块间电池SOC的均衡,未向VSG控制引入SOC偏差反馈信息,系统输出电压、电流畸变较小。但BESS中H桥子模块存在2倍工频的电压、电流脉动,其对电池SOC检测等方面的影响还需进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 陈国平,李明节,许涛,等.关于新能源发展的技术瓶颈研究[J].中国电机工程学报,2017,37(1):20-27.

CHEN Guoping, LI Mingjie, XU Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-27.

[2] 张丽英,叶挺路,辛耀中,等.大规模风电接入电网的相关问题及措施[J].中国电机工程学报,2010,30(25):1-9.

ZHANG Liying, YE Tinglu, XIN Yaozhong, et al. Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE, 2010, 30(25): 1-9.

[3] 康重庆,姚良忠.高比例可再生能源电力系统的关键科学问题与理论研究框架[J].电力系统自动化,2017,41(9):2-11.DOI:10.7500/AEPS20170120004.

KANG Chongqing, YAO Liangzhong. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2017, 41(9): 2-11. DOI: 10.7500/AEPS20170120004.

[4] YAO L Z, YANG B, CUI H F, et al. Challenges and progresses of energy storage technology and its application in power systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 3-8.

[5] 张峰.高压级联储能功率转换系统控制策略研究[D].上海:上海交通大学,2013.

[6] SHARMA R, SINGH M, JAIN D K. Power system stability analysis with large penetration of distributed generation[C]// 2014 6th IEEE Power India International Conference, December 5-7, 2014, New Delhi, India: 1-6.

[7] 王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.

WANG Chengshan, LI Peng. The impact of AMI on the future power system[J]. Automation of Electric Power Systems, 2010, 34(2): 10-14.

[8] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150508006.

ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150508006.

[9] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators [J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1266.

[10] 魏亚龙,张辉,孙凯,等.基于虚拟功率的虚拟同步发电机预同步方法[J].电力系统自动化,2016,40(12):124-129.DOI:10.7500/AEPS20150727006.

WEI Yalong, ZHANG Hui, SUN Kai, et al. Pre-synchronization method of virtual synchronous generator using virtual power[J]. Automation of Electric Power Systems, 2016, 40(12): 124-129. DOI: 10.7500/AEPS20150727006.

[11] 石荣亮,张兴,刘芳,等.提高光储柴独立微网频率稳定性的虚拟同步发电机控制策略[J].电力系统自动化,2016,40(22):77-85.DOI:10.7500/AEPS20160322016.

SHI Rongliang, ZHANG Xing, LIU Fang, et al. Control strategy of virtual synchronous generator for improving frequency stability of islanded photovoltaic-battery-diesel microgrid[J]. Automation of Electric Power Systems, 2016, 40(22): 77-85. DOI: 10.7500/AEPS20160322016.

[12] WU Heng, RUAN Xinbo, YANG Dongsheng, et al. Small-signal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4292-4303.

[13] 马泽宇,姜久春,文锋,等.用于储能系统的梯次利用锂电池组均衡策略设计[J].电力系统自动化,2014,38(3):106-111.DOI:10.7500/AEPS20130330001.

MA Zeyu, JIANG Jiuchun, WEN Feng. Design of equilibrium strategy of echelon use Li-ion battery pack for energy storage system[J]. Automation of Electric Power Systems, 2014, 38(3): 106-111. DOI: 10.7500/AEPS20130330001.

[14] 亢玖慧.混合级联多电平储能充放电变换器研究[D].吉林:东北电力大学,2013.

[15] 艾洪克,吴俊勇,郝亮亮,等.级联式储能系统中电池自均衡控制策略研究[J].电工技术学报,2015,30(14):442-449.

AI Hongke, WU Junyong, HAO Liangliang, et al. Research on battery self-balancing control strategy in cascade energy storage system[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 442-449.

[16] 中国国家标准化管理委员会.电能质量供电电压偏差:GB/T 12325—2008[S].北京:中国标准出版社,2008.

[17] 中国国家标准化管理委员会.电能质量电力系统频率偏差:GB/T 15945—2008[S].北京:中国标准出版社,2008.

[18] SHINTAI T, MIURA Y, ISE T. Oscillation damping of a distributed generator using a virtual synchronous generator [J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676.

[19] KAWAKAMI N, OTA S, KON H, et al. Development of a 500-kW modular multilevel cascade converter for battery energy storage systems[J]. IEEE Transactions on Industry Applications, 2014, 50(6): 3902-3910.

[20] MIRANBEIGI M, IMAN-EINI H. Hybrid modulation technique for grid-connected cascaded photovoltaic systems[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12): 7843-7853.

李 新(1993—),男,通信作者,博士研究生,主要研究方向:大功率新能源并网与控制技术、储能技术。E-mail： xin_li@zju.edu.cn

杨苒晨(1996—),女,博士研究生,主要研究方向:微电网控制及储能技术。E-mail: yangranchen@163.com

邵雨亭(1993—),男,硕士研究生,主要研究方向:电能质量及数字控制技术。E-mail: yuting_shao@foxmail.com