跳出排列组合的“误区陷阱”
张津航
(河北省乐亭县第一中学 063600)
排列组合问题虽然种类繁多,稍不注意就会产生这样或那样的错误,但只要能把握住最常见的原理和方法,即:“分步用乘、分类用加、有序排列、无序组合”,留心容易出错的地方就能够以不变应万变,把排列组合学好下面我们给出一些排列组合问题的一些典型错例解析,以期能够帮助大家起到防微杜渐的作用.
一、没有理解两个基本原理出错
排列组合问题基于两个基本计数原理,即加法原理和乘法原理,故理解“分类用加、分步用乘”是解决排列组合问题的前提.
例1 从6台原装计算机和5台组装计算机中任意选取5台,其中至少有原装与组装计算机各两台,则不同的取法有 种
错解因为可以取2台原装与3台组装计算机或是3台原装与2台组装计算机,所以只有2种取法.
错因分析误解的原因在于没有意识到“选取2台原装与3台组装计算机或是3台原装与2台组装计算机”是完成任务的两“类”办法,每类办法中都还有不同的取法.
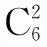
二、重复计算出错
在排列组合中常会遇到元素分配问题、平均分组问题等,这些问题要注意避免重复计数,产生错误.
例2 5本不同的书全部分给4个学生,每个学生至少一本,不同的分法种数为( ).
A.480 种 B.240种 C.120种 D.96种
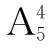
错因分析设5本书为a、b、c、d、e,四个人为甲、乙、丙、丁按照上述分法可能如下的表1和表2:
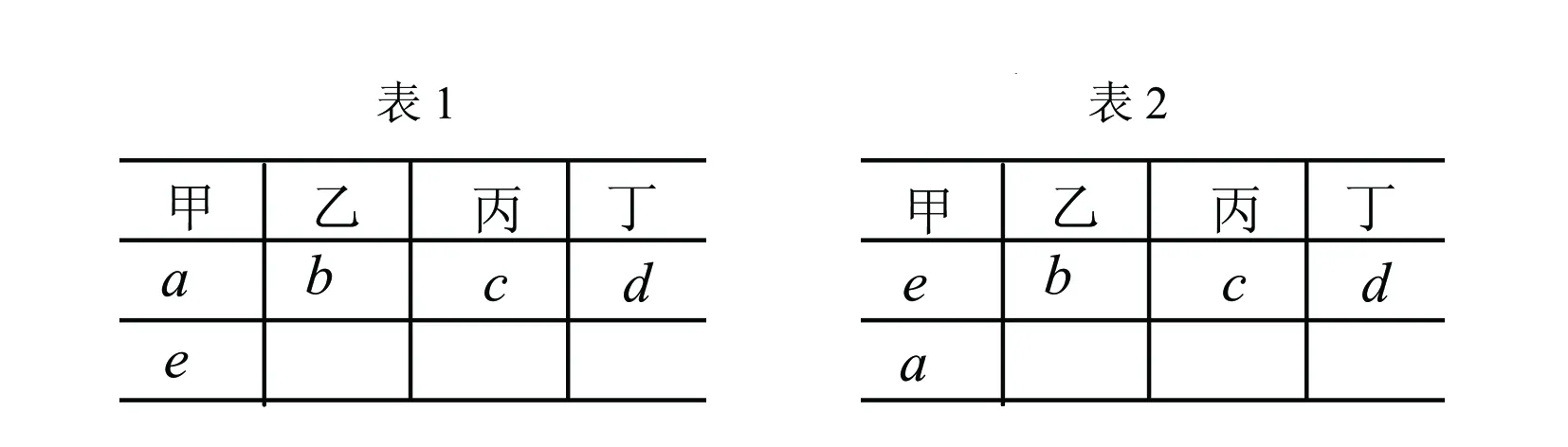
表1是甲首先分得a、乙分得b、丙分得c、丁分得d,最后一本书e给甲的情况;表2是甲首先分得e、乙分得b、丙分得c、丁分得d,最后一本书a给甲的情况这两种情况是完全相同的,而在误解中计算成了不同的情况.正好重复了一次.
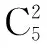
三、忽视题设条件出错
在解决排列组合问题时一定要注意题目中的每一句话甚至每一个字和符号,不然就可能多解或者漏解.
例3 如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有____种(以数字作答).

错因分析据报导,在高考中有很多考生填了48种这主要是没有看清题设“有4种颜色可供选择”,不一定需要4种颜色全部使用,用3种也可以完成任务.
四、未考虑特殊情况出错
在排列组合中要特别注意一些特殊情况,一有疏漏就会出错.
例4 现有1角、2角、5角、1元、2元、5元、10元、50元人民币各一张,100元人民币2张,从中至少取一张,共可组成不同的币值种数是( ).
A.1024种 B.1023种 C.1536种 D.1535种
错解因为共有人民币10张,每张人民币都有取和不取2种情况,减去全不取的1种情况,共有210-1=1023种.
错因分析这里100元面值比较特殊有两张,在误解中被计算成 4 种情况,实际上只有不取、取一张和取二张3种情况.
正解除100元人民币以外每张均有取和不取2种情况,100元人民币的取法有3种情况,再减去全不取的1种情况,所以共有29×3-1=1535种.
参考文献:
[1]张明艳.排列组合问题中的思想方法[J].课程教育研究,2015(09):204-205.
[2]冯芮.排列组合解题的常用策略[J].科教文汇(下旬刊),2014(05):137-138.

