以题为鉴,激活思维
——一道高考题在高三复习中的教学运用
林月霞
(广东省江门市棠下中学 529000)
一、题目分析
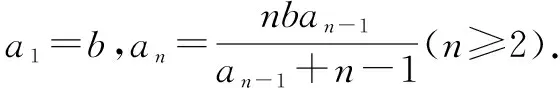
(1)求数列{an}的通项公式;
(2)证明:对于一切正整数n,2an≤bn+1+1.
纵观这个题目,主要考查的是分式型递推数列,解决它有一定的技巧性,必须先倒过来作一个处理才能转化成线性递推关系,才可以利用我们平时训练的比较多的构造法来求数列通项.但是这个题目除了是分式型递推数列外还涉及到字母,增加了难度,很多学生碰见这种题时就慌了阵脚,不知该从何下手,以致当年高考中该题收获甚微.
二、以题为鉴,设计教学
不论从选拔人才的要求,还是贯切新课标的基本理念,高考题都必然考查学生的创新意识.高考题就像一个风向标,为下一年的复习指明了一定的方向,我们必须从高考题中吸取一些经验与教训,在教学上通过优化课堂结构,开展不同形式的探究活动,并且采取逐层深入的方式,激发学生的创造力,使学生的解题思维与解题能力得到升华,籍此提高我们高三复习的教学效能.
下面就围绕这个题目进行这样的一个教学设计.
教学目标:通过分层设计几个求数列通项的例题,让同学们进一步掌握怎样用构造法来求数列的通项.
教学过程:
例1 已知数列{an}中,a1=1,an=2an-1+3(n≥2),求数列{an}的通项公式.
点评该题是形如a1=b,an=pan-1+q(p,q为常数且n≥2)的类型,可以用构造等比数列法来求数列的通项.因为之前我们对这种题目训练得比较多,所以学生对此比较熟悉,很快就把问题解决了.
例2 设b>0,已知数列{an}中,a1=b,an=pan-1+q(p,q为常数且n≥2),求数列{an}的通项公式.
点评该题是例1的推广情形,例1题目中的系数都是常数,而这里是字母,而且要对p进行分类讨论,增加了题目的难度,令利用构造法求通项的问题更加有代表性.
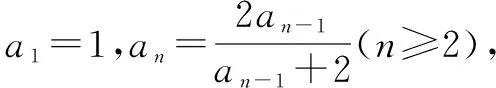
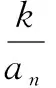

点评该题是例3的一般情形,例3题目中的系数都是常数,而这里都是字母,对等式两边取倒后就变成我们熟悉的线性递推关系,再用构造法求通项.但这里的系数比较繁琐,计算比较复杂,还要对字母进行分类讨论.
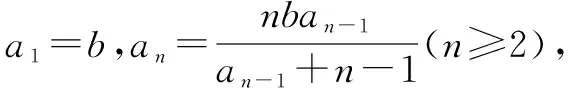
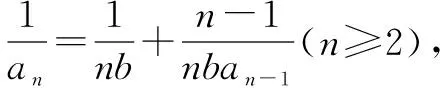
教学效果:这节课的题目设计环环相扣,层层递进,学生积极参与思考,思维活跃,直到最后,在师生的共同努力下终于揭开高考题的庐山真面目,学生感受到思考的快乐和成功的喜悦!教师也感受到育人的成就感.
三、对高三复习课教学的启示
1.精选题目,避免题海战术
在信息高度发达的今天,各种各样的高考复习辅导资料非常多,只有教师走进题海,学生才能走出题海.所以我们必须对各地各类资料、信息试卷中的题目等进行变式处理.坚决反对试卷一发,学生一做,随便一看,答案一对的重复、粗放、低效的训练方法.训练完后要求学生“借题发挥(反思)”.要进行“四类反思”,它是怎么生成的?它适用于哪一类(而不是哪一个)问题?它要考你什么——题中隐含有哪一种学科思想?它还可以生出哪些变式?
2.在学生的就近发展区域内精心设计课堂教学,提高教学效能
课堂教学是我们教学工作的一个中心环节,大部分
的知识、方法都是在课堂中生成.笔者的这节课堂设计,让学生从熟悉的题目做起,再以此为基础深入展开,层层递进,把问题设计在学生的就近发展区域内,让他们跳一跳就可以尝到成功的喜悦,既能激发学生的学习数学热情,又能达到锻炼学生的思维能力的目的,一举两得,这一节复习课达到了良好的教学效能.解题教学不能为解题而解题,不能只追求解题的数量和结果,而应注意解题过程的体验、分析和研究,不断总结经验,发现规律,提高解题的训练价值和教学效率.
我们常说高考是一根指挥棒,而高考试题则是指挥棒上明亮的标志,引领着我们高考复习的方向.只要平时我们多研究高考题,明确命题趋向,利用它潜在的价值,在课堂上进行延伸教学,那么我们的教学必定有意想不到的效果.
参考文献:
[1]李召存.课程知识论[M].上海:华东师范大学出版社,2009.
[2]陈柏良.教学立意:优质课堂教学建构的基石[J].数学通报,2011(8).

