在高三复习课中培养数学核心素养*
●
(义乌市第六中学,浙江 义乌 322000)
数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现.数学核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学学科核心素养既相对独立又相互交融,是一个有机整体[1].
数学核心素养是在数学学习和应用的过程中逐步发展的,是通过数学的反思、积累、升华孕育出来的.如何在高三的数学教学过程中落实德育,又充分发挥习题课的功能,教会学生“以不变应万变”,在减负中提升学生的数学核心素养.笔者以一道改编的高考解三角题为例,对它进行了多角度思考和分析,以提升学生的思维广度和深度,从而达到培养数学核心素养的目的.
1 问题提出
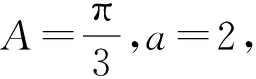
(2013年全国数学高考新课标卷Ⅱ理科试题第17题改编)
分析解三角形主要考查的是正弦定理、余弦定理及其应用,其实质是已知三角形的几个元素求其他元素的过程.具体来看主要分为以下两类:1)已知3个量,求解另外3个量;2)已知2个量,求取值范围(最值).此题属于解三角形的第二种类型,具体解法如下:
2 解法分析
思路1(余弦定理+基本不等式法)由已知条件及余弦定理得
a2=b2+c2-2bccosA,
从而
4=b2+c2-bc≥2bc-bc=bc,
当且仅当b=c=2时等号成立,于是
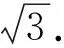
评注思路1利用余弦定理化角为边,进而根据基本不等式求出bc的取值范围.从课堂教学情况来看,多数学生能从这个角度去思考和解题.
思路2(正弦定理+三角函数)由正弦定理得
即
b=2RsinB,c=2RsinC,
从而
bc=(2R)2sinBsinC.
又因为在△ABC中,
sinBsinC= sinBsin(A+B)=
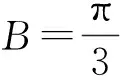
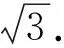
评注思路2利用正弦定理化边为角,把问题转化为三角函数的范围问题,结合三角函数图像性质来解决bc的取值范围.在教学中,多数学生不容易从这个角度去思考,少数学生化到bc=(2R)2sinBsinC这一步之后,因不知道如何处理双变量问题而停止了.在充分理解运算对象的基础上,将双变量的问题转化为单变量的三角函数的范围问题,利用三角函数这一强大工具来解决问题,有利于培养学生的数学运算核心素养.
思路3(齐次化思想)本题等价于“已知b2+c2-bc=4,求bc的最大值”,其实质是“在二元约束条件下求二元目标函数的范围(最值)问题”.可将目标函数齐次化:
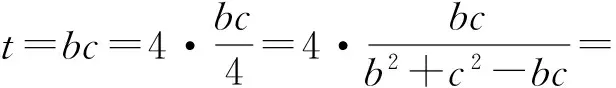
当且仅当b=c时等号成立,从而bc≤4,即
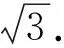
评注思路3从具体的背景中抽象出了一般的数量关系,概括出了问题的本质,认识了数学结构与体系,有利于培养学生的抽象核心素养.
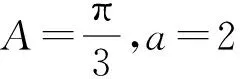
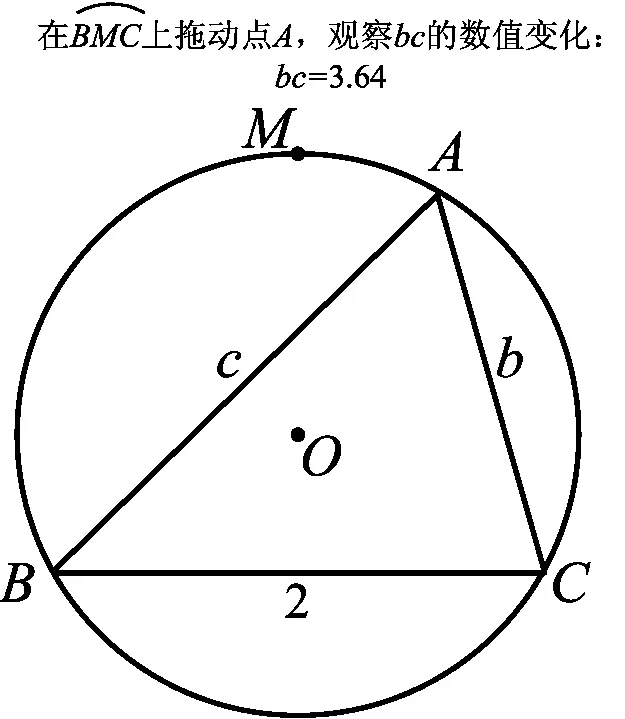
图1
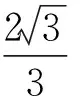
(先定性分析)由对称性知,我们可以只需考虑半边的情况,即动点A从端点B靠近点M(或动点A从端点C靠近点M)这一过程.当点A在点B附近时,b→2,c→0,其乘积bc→0;当点A在点M处时,b=c=2,其乘积bc=4.如图1,借助几何画板的动态演示,可观察出其变化过程.最终可得bc≤4,即
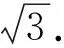
(再直观分析)当点A运动到点M处时,面积达到最大值(因为底BC=a=2为定值,当△ABC的高达到最大时,其面积也最大,显然在点M处时,高最大).此时△ABC为正三角形.
评注思路4从动态、直观的角度来解决问题,认识了数与形的关系,在解决问题的过程中,有利于培养学生直观想象的核心素养.
3 变式与拓展
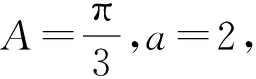
设计说明巩固以上的几种常见方法,体会解三角问题的基本思想:“统一”,即统一化成角或统一化成边的形式;体会两种常见的思路,利用正、余弦定理进行统一化.在比较的过程中选择自己擅长的方法,更重要的是学会“一角及对边的模式”的常见处理方法.

设计说明比较上述方法的优缺点,要根据具体问题进行具体的分析.思路1和思路3不能较好地体现锐角这一限制条件;思路2的关键是要分析出角度的范围;思路4中点的运动轨迹范围变小了.
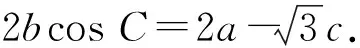
1)求∠B的大小;
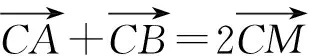
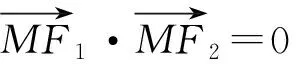
4 反思与回顾
高三复习课的首要任务是让学生的知识连成线、铺成面、织成网,教师要跳进题海,追本溯源,总结问题的变式及拓展,加深对问题本质的认识,重构知识网络.只有这样的深度学习,才能有效提高数学核心素养.
[1] 中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2017.

