数字电路中卡诺图的更多应用研究

(天津市河东区职工大学，天津 300162)

1 前言

卡诺图(karnaugh map)是逻辑函数的一种图形表示方法，由美国贝尔实验室的电信工程师莫里斯·卡诺(Maurice Karnaugh)发明，在函数化简、故障诊断、数字逻辑等许多领域中应用广泛。

2 基本应用——逻辑代数化简

逻辑代数化简在数字电路中是非常必要且重要的，经过化简的电路不仅节省原材料降低成本而且可以提高电路稳定性有助于后期维护维修。常用的化简方法包括代数化简法和卡诺图化简法。卡诺图化简法具有直观、准确、步骤清晰等特点应用较多，但在化简变量个数上有限制目前适用于2-4变量的函数化简，对于更多变量的化简就略显复杂。

2.1 卡诺图化简方法及技巧

这里我们以2-4变量卡诺图为例总结一下卡诺图化简的基本方法和在化简过程中的技巧及需要遵循的原则。

2.1.1 卡诺图中“0”和“1”的填入方法

依据变量个数选择卡诺图框架是化简的第一步，两变量的函数画4格图，三变量的函数画8格图，四变量函数画16格图。卡诺图的每个方格代表一个最小项，在题目中出现的最小项在卡诺图中填入“1”，没出现的填入“0”，填满后再化简。有时原题目中直接给出真值表、或者是非最小项的表达式再或者只有最小项编号，这些情况如果按照先变成最小项表达式再填入卡诺图的方法，会涉及将非最小项变成最小项的补项过程，其过程之繁琐不亚于代数化简，已经失去用卡诺图化简的简单、快捷的意义，所以我们在彻底理解卡诺图中的每一个方格所代表的含义基础上，应该掌握各种已知条件下都可以直接画出卡诺图的方法。下面是三种需要直接画出卡诺图的情况。

2.1.1.1 由真值表直接画出卡诺图

以三变量奇偶校验器为例 。首先把表中输出为1的项所对应的输入组合填入卡诺图对应方格中，在卡诺图方格中横行代表变量A的取值分别为0和1,纵向4列分别代表BC的取值依次为00、01、11、10也就是变量B依次取值为0、0、1、1，变量C依次取值为0、1、1、0。如输入为001，输出为1，代表A=0，B=0，C=1时输出F=1，那么A=0，B=0，C=1的输入组合对应的方格就是卡诺图中第一行第二列相交的位置，所以在此格处填上1，按照此方法将其他输出为1的项依次填入卡诺图，最后空白格处填入0即可，这样就完成了由真值表直接画出卡诺图的过程。

2.1.1.2 非标准与或式直接画出卡诺图

2.1.1.3 由最小项编号直接画出卡诺图

有些题目会给出最小项编号的求和形式，这时我们也要直接将卡诺图画出再化简，卡诺图的每一个小方格代表一个最小项同时最小项的二进制编码对应一位十进制数，这样就可以根据最小项的编号直接填入到相应的方格，在题目中出现最小项编号的项就填入1。图2-1表示每一个方格所代表最小项的编号。

在填入卡诺图变量时直接找对应编号所在位置填入即可，如下式

F(A,B,C,D)=∑m(0,1,2,3,14,15),该式表示最小项m0、m1、m2、m3、m14、m15,这6个最小项相加求和，在式中出现的最小项编号0、1、2、3、14、15的位置上填入1，其他位置上填入0再化简。填完后如图2-2所示

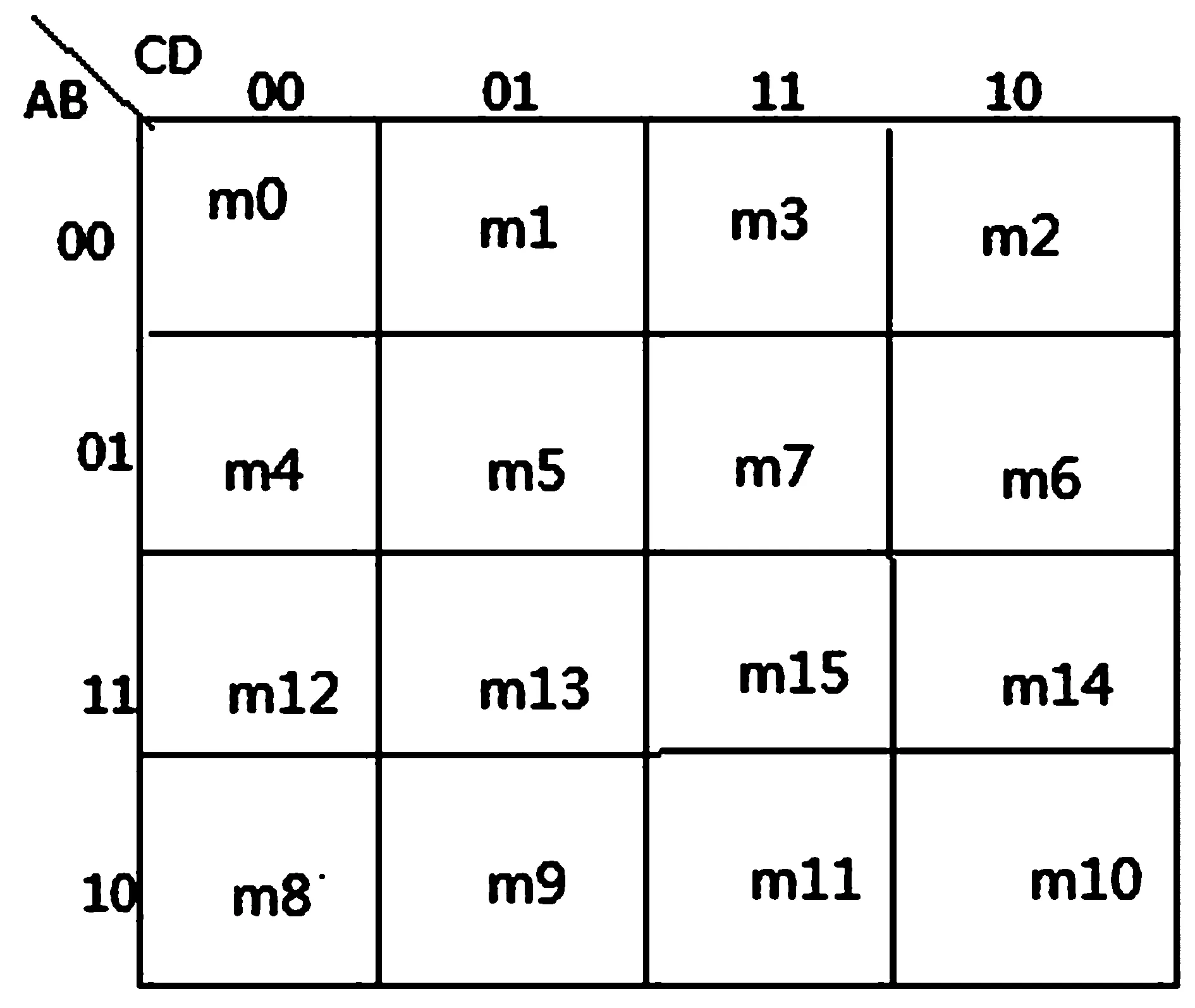
图2-1 含最小项编号卡诺图框架

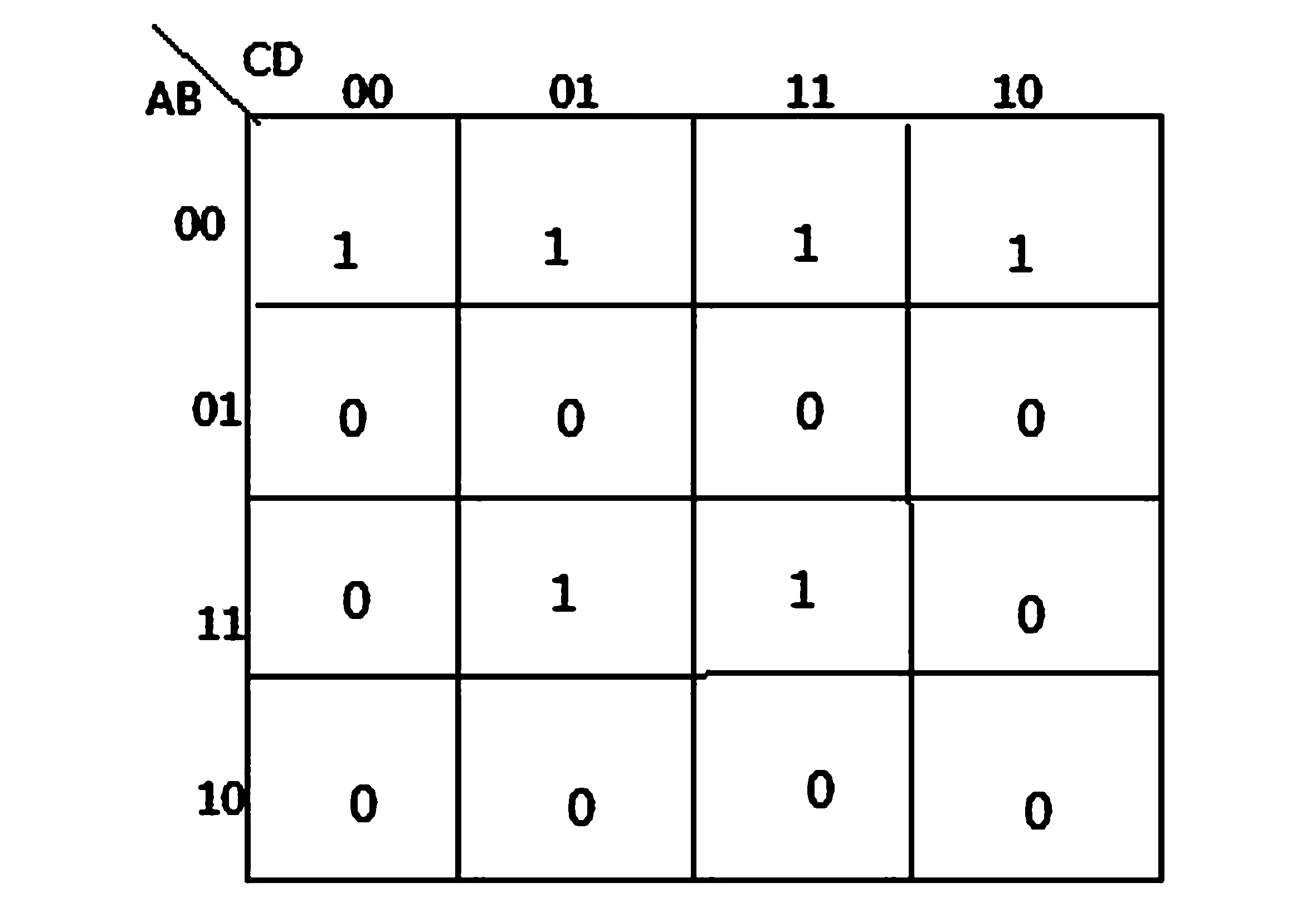
图2-2 F(A,B,C,D)=∑m(0,1,2,3,14,15),卡诺图

以上是三种特殊情况下填入卡诺图中0和1的方法，直接填入0和1直接画出卡诺图才能直接化简函数式，减少化简繁琐性。

2.1.2 卡诺图特殊相邻关系及合并规律

卡诺图化简其实就是合并相邻最小项。正确判断相邻关系、准确写出每一个卡诺圈对应的与项是化简的关键。有些特殊位置的相邻需要特殊注意，如图2-3所示。

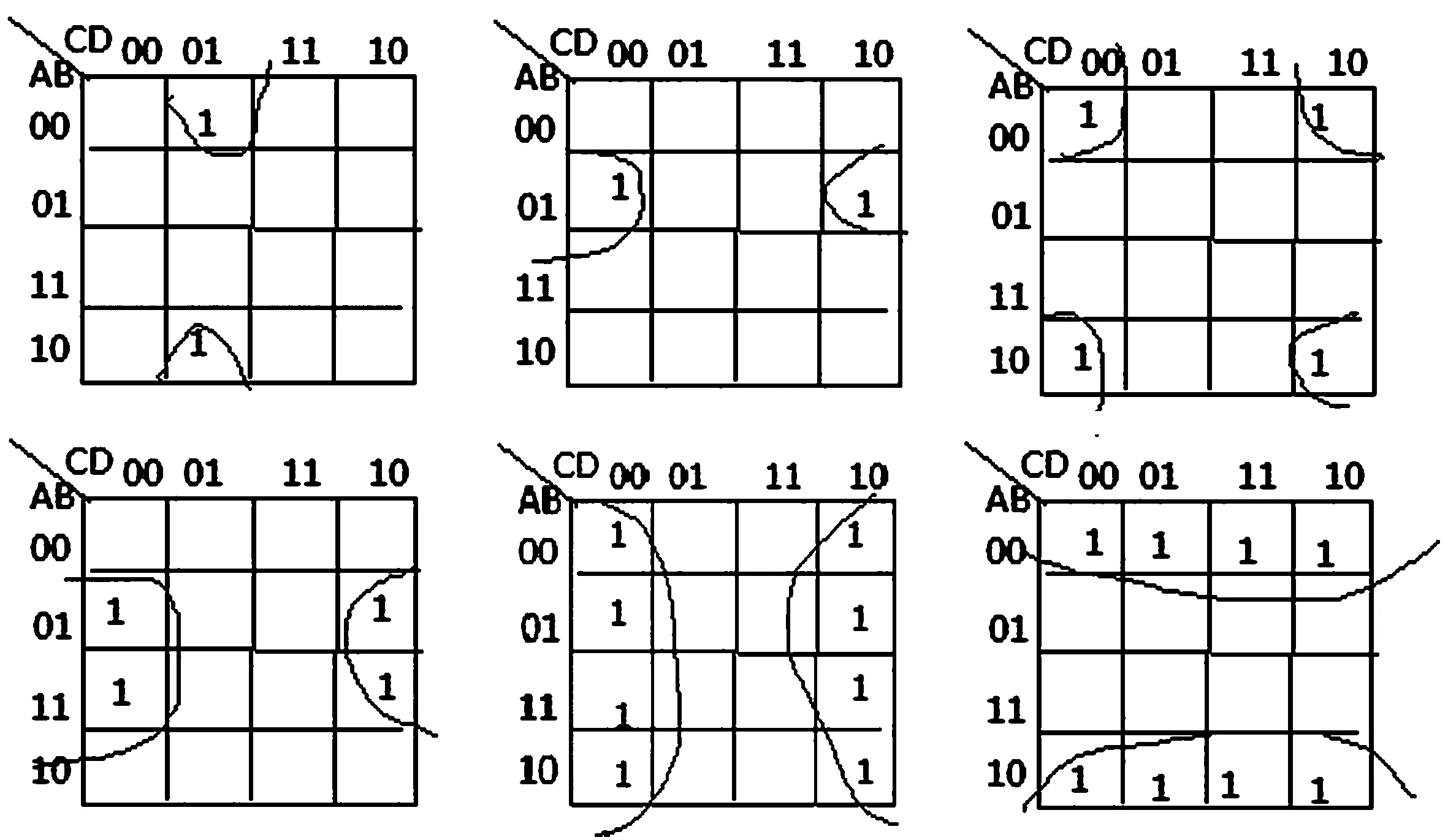
图2-3 特殊相邻关系的卡诺图

卡诺图是上下、左右闭合的图形，因此卡诺图的最上行和最下行，最左列和最右列都是位置相邻的，四角相邻也是特殊位置之一，单独一个格四周都是0的情况也要单独画出一个卡诺圈。在合并的时候还要注意以下几点：

一是，所圈取值为1的小方格的个数应为2n(n=0,1,2,3,…)即所圈格数为1,2,4,8……不允许3,6,10,12等。

二是，合并目的就是保留一个圈内最小项的相同变量，除去不同变量。相邻的两项可合并为一项，并消去一个因子，相邻的四项合并为一项，可以消去两个因子，以此类推，相邻的2n可合并为一项消去n个因子。

三是，注意相邻关系包括最上行和最下行，最左列和最右列的位置。

2.1.3 卡诺图化简原则

其一，卡诺圈越大越简单。因为一个卡诺圈就是一个与项，卡诺圈越大包含的最小项越多，消去的变量就越多，与项就越简单，化简后的表达式就越简单。

其二，卡诺圈数越少越简单。因为一个卡诺圈就是一个与项，卡诺圈越少与项就越少，与或表达式就越简单。

其三，卡诺图中所有的1都要被圈过，圈过的1可以被重复再圈，但每一个新的卡诺圈都要包含新的1。

2.1.4 卡诺图化简之画“0”求反函数

在进行卡诺图化简时，有时方格中填入1的个数远远多于填入0的个数，这时我们可以通过画0求反函数，再求原函数的方法化简，这样可以减少画更多卡诺圈的过程，但这种方法要求会正确求原函数，否则结果反倒出错，个人建议还是圈1即可，因为1占的方格数多相邻的项就多，得到的与项就简单，求得原函数更直接。

3 卡诺图更多应用探究

3.1 无关项应用技巧

数字电路中的无关项是随意项和约束项的统称。在一些实际应用中，某些输入组合不会出现或者不允许出现(即输入变量必须遵守一定的约束条件)或者当某些输入组合出现时输出可为任意值。这些情况的共同点是输出值是未指定的(或随意的)，称这些输入组合所对应的最小项为随意项，用“Φ”、“×”、“d”表示。在化简时可以将其视为“0”或“1”以求最简函数式，而约束项是值恒为0的最小项，在化简时当做0看待。如在8421BCD码中1010、1011、1100、1101、1110和1111是不允许出现的便是无关项。无关项之和也叫约束方程如∑d(10、11、12、13、14、15)=0。再如七段显示译码器中的各个字段都有约束方程，才使得其完成各字段正常显示0-9十个数字的功能，在化简时在图中把无关项视为1看待扩大卡诺圈使与项更简单， 在实际中也可以把无关项看做0使用，无关项的随意性和可塑性是我们在进行化简时的有力辅助工具。

3.2 用卡诺图判明函数关系和进行逻辑运算

3.2.1 判明函数关系

利用卡诺图可以判断函数式是相等关系还是互补关系

3.2.1.1 判断相等关系

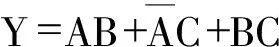
图3-1 函数相等关系

3.2.1.2 判断互补关系

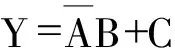
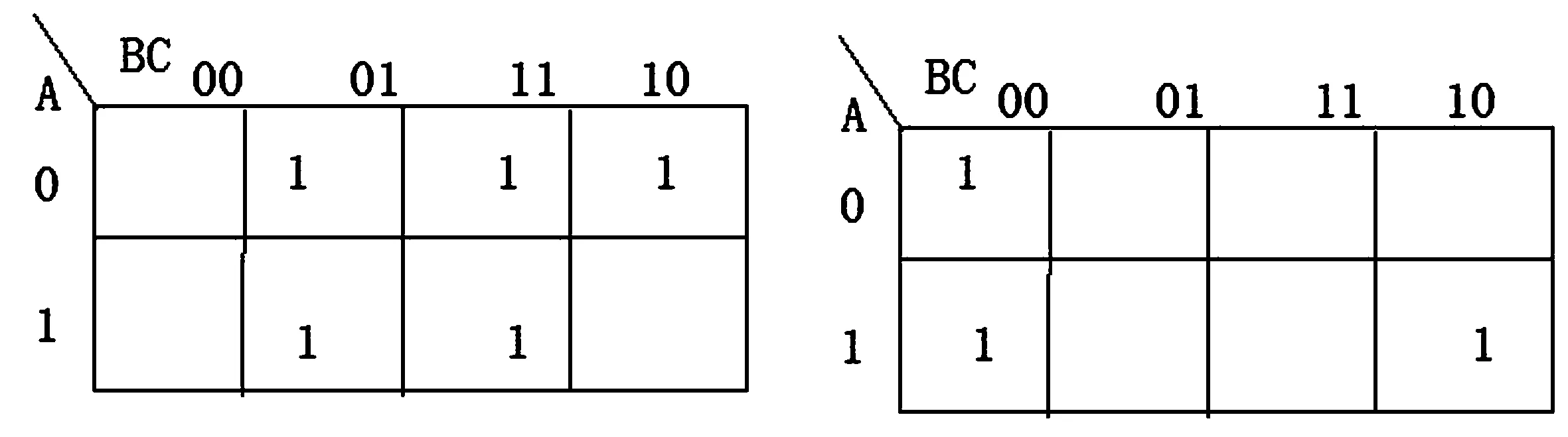
函数式的卡诺图 函数式的卡诺图图3-2 函数互补关系

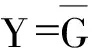
3.2.2 进行函数运算

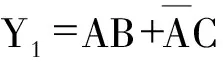
Y1·Y2与运算： 仅当所有输入为1 时，输出才为1，只要有输入为0，输出便是0。

Y1+Y2或运算：只要有一个输入为1输出便是1；只有所有的输入皆为0，输出才为0。

异或运算：输入信号不同时输出为1；当输入信号相同时输出为0。

同或运算：输入信号相同时输出为1；当输入信号不同时输出为0。将Y1和Y2的卡诺图合并。

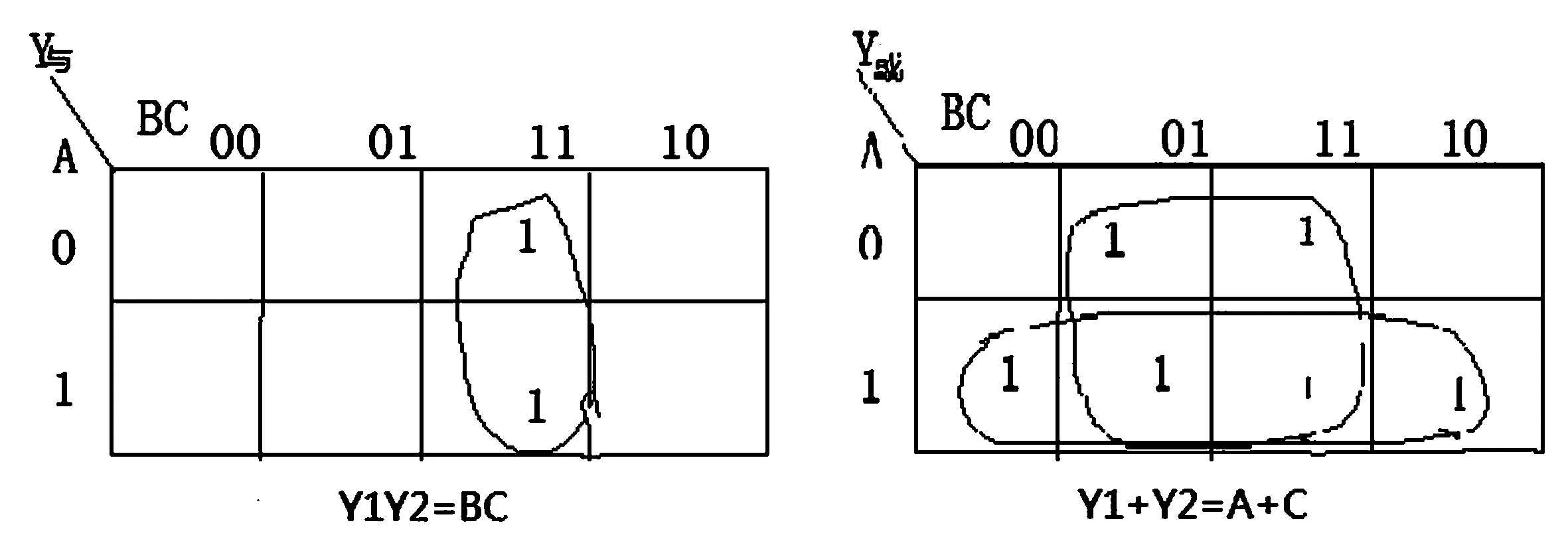
如图3-3所示

图3-3 四种运算结果卡诺图

上图显示利用卡诺图进行逻辑代数四种运算的实现过程，直观、简单、准确，卡诺图是进行逻辑运算的有力工具，除了以上四种运算还可以进行其他扩展运算，这里不再详述。

3．3 判断并消除竞争和冒险

3.3.1 竞争冒险的定义

竞争冒险，是数字电路中一种特有的现象。理想状态下电路输入输出没有延时现象，但实际电路是有传输延时的，因门电路连接方式不同延时时间也不同，使得各输入信号状态改变时刻有先有后而产生时差。这种引起时差的现象称为竞争。竞争使稳定的输出状态出现逻辑关系短暂破坏，产生尖峰脉冲，这种现象就叫做“冒险”。冒险可能使电路产生暂时或永久的逻辑错误，所以在进行逻辑电路设计时一定要提前判断竞争和冒险的存在并且将其消除，以保证电路的正常运行。判断和消除竞争冒险的方法很多，卡诺图是方法之一并且该方法简单、直观。

3.3.2 判断组合逻辑电路是否存在竞争冒险的一般步骤

首先画出待判断的组合逻辑电路的卡诺图，然后在卡诺图上画出和表达式中所有乘积项一 一对应的卡诺圈，如果卡诺图中存在相切的卡诺圈，则此逻辑电路存在着竞争冒险的情况。这里所说的卡诺圈相切是指两个卡诺圈之间存在不被同一个卡诺圈包含的相邻最小项。

3.3.3 消除竞争和冒险的方法

4 总结

通过以上的探究我们看到了卡诺图除了化简之外的其他应用，这些应用在平常不经常使用也不是必须教授内容，但是它的使用却能比很多现有常规方法更简单快捷的解决问题，为数字逻辑电路的分析和应用打开新的窗口，有待我们去熟悉应用并进一步探究其更多的应用。

参考文献：

[1]孙健.数字电子技术基础[M].重庆：西南交通大学出版社,2009.

[2]刘宝琴,沈雅芬.计算机电路基础[M].北京：中央广播电视大学出版社,2004.

[3]夏奇兵.电子技术基础[M].北京：机械工业出版社,2008.