微积分求导问题考辩与新解(上)——一种不需要极限与无穷小概念的微积分理论诠释

(西北工业大学前逻辑与人工智能研究所，西安 710072)

一、除法的本质及最简单的自函数问题分析

微积分标准分析中极限法求导数过程中，极限根本就不存在的问题，笔者在文献2、7中已经表述的很详尽了。鉴于这个问题统治微积分理论很长时间，因此这里再给出一个较为严密的证明(简单起见，同时不失一般性，就以自函数和二次函数为例)：

由文献2中的公式3、4、5(即本文的公式6)可知，这是二次函数明确无误的求导公式。如果文献2中公式2表示的传统二次函数求导过程也成立，则它们必然相等。由此可以推知、并且由自函数也可以直接推出(文献7)，此时必有关系：

(1)

但显然我们已有：

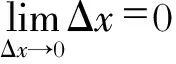
(2)

以及：

(3)

特别应该注意，由公式3，作为极限，分母上完全可以等于0。于是，由2、3式，我们可得：

(4)

可以清楚地看出，自函数的增量比值函数在自变量趋于0时的极限，明确为0/0，而不是1。也就是绝非其导数1，得证。

当然，这里必须说明，严格讲公式3中的∞所对应的，应该是分母为无穷小ε，而不是分母为0，分母为0所对应的，只能是“无意义”。这里是一种通常并不严格但又常用的写法。因此，我们不妨把公式3中的∞，就理解成“无意义”，这并不影响讨论结果。

总之，事情的本质是：既然经常在教科书中出现的公式3确定了分母上的极限值可以为0，那么对于作为导数的原始定义增量比值函数而言，我们就应该老老实实地直接对分母上的自变量取为0的极限。而不是“无意中地”把分母上的自变量先“消去”(分子分母做除法)再求极限。此时求得的极限，是另一个分母上不出现自变量的函数的极限，而不是原先的增量比值函数也就是作为导数原始定义的那个函数的极限。即：除非不定式0·∞=0·(1/0)=0/0=1/1=1，我们不可能由自函数的增量比值函数在自变量△x→0时的极限求出其导数1，因为显然，这个极限为不定式(即0/0)，也就是根本就没有确定的、有意义的值。也就是说，我们明明要求的是分母上有△x的函数A在0点的极限，但却“无意中”通过除法“消去”了分母上的这个△x，因此实际求的是分母上已经没有了△x的函数B在0点的极限，还说此极限就是函数A也就是分母上有△x的那个函数在0点的极限。甚至当笔者指出此点时，有人还说只要△x不为0，就可以相除消去它。他们忘了，分子分母相除消去分母上的△x的另一个前提是分母上的△x不能取其在0点的极限值0，但这里恰恰其极限值就是0。直观理解：设△y=△x，当△x=0时，必有△y=0，此时自然△y/△x=0/0。同理，当△x→0时，也有△y→0，此时自然△y/△x→0/0(当然这个0/0不是“有意义”的函数值或极限值，但这是另一回事。也就是先要其存在，才能确定其是否“有意义”)。因此，就求极限而言，先消去分母上的△x以求分母上明明有△x的函数在△x=0时的极限值在逻辑上是不能被允许的。可是，所谓标准分析的极限法求导，恰恰就是这么干的，因此它只能是错误的。

鉴于这个问题的重要性，我们这里可以给出一个更为严格的反证法的证明：如欲一分母上有自变量△x的式子(函数)在△x=0点有分母不等于0的“有意义”的极限值K，只能是其分母上再无△x，即通过分子分母的相除消去原式(函数)中分母上的自变量△x，也就是在保持原式的值不变时，分母上的自变量△x=1，因此可以写为K/1，也就是式中分子分母上的△x有值△x/△x=1/1。而这个所谓“消去”分母上的自变量△x的除法的前提条件(充分必要条件)，不仅要求式中分母上的△x≠0(作为也仅仅作为必要条件之一)，同时也不能有为0的极限值(如果当分母上的△x→0时竟然有极限值为1，即等于△x→1时的极限值，这当然不可能。详细论证见前面公式1～4的证明；如果当分母上的△x→0时有极限为0，则比值函数在0点必有极限0/0，当然不行；而如果以不允许或没有△x→0作为除法的先提条件之一，则当然得不到我们希望在△x→0时才会得到的分母不为0的极限值K)。即如果分母上有自变量△x，则不能有△x→0。而原式中分母上有△x，所以原式不能有△x→0时的有意义的极限值(也可以说极限与其函数值一样，也是0/0)。可见，标准分析的所谓极限法求导，实际陷入了逻辑上的循环论证，也就是：有意义的极限值的(分母无自变量△x→0的非0/0型的)求出要求分子分母先做除法消去分母上的△x，而这个除法又要求分母上的自变量△x不能趋于0(取为0的极限值)。退一步说，即使在分母有极限0的前提下也可以分子分母相除，但相除后求出的分母不为0的极限值显然与前提矛盾，这还有意义吗？因此这个方法当然不能成立。

此外，尽管除法的前提是分母上的△x≠0，但反之满足这个条件的分式可并不一定非做除法。没有一条数学规定要求逢分式必须做除法消去分母的。因此显然，如果不做除法，在分母上保留△x，则虽然其始终不能等于0，但按“不可达极限”的定义，它仍然可以趋于0而以0为其极限值。也就是得到极限0/0，这当然是所谓“无意义的”极限值，但也必须先要得到它，才知道它的无意义。因此，这里不存在在0点无有意义的函数值(函数值为0/0)而有有意义的极限值(非0/0型的极限)的情况出现。总之，无论分式除(即消去分母上的△x或令其等于1)与不除(不消去分母上的△x)，都无有意义的极限值，得证。

我们也可以用类比法帮助理解这个问题：函数△x/△x在△x=0点之值为0/0(虽然不是个有意义的函数值。这个虽然是“无意义”的“函数值”是必须要有的，因为标准分析的极限法正是根据此点也就是有0/0型的、无意义的“函数值”才可能再认定在△x=0点没有有意义的、也就是没有非0/0型的函数值，进而在该点的求极限才有必要)，于是对有意义的函数值而言，该函数在△x=0点无定义。该函数在△x=1点之值显然为1/1也就是1。现在设该函数在△x=1点上也无定义，也就是在此点也没有函数值或函数的定义域不包括此点。但显然，此时该函数在△x=1点虽然没有函数值1，但却可以有极限值1。于是同理，该函数在△x=0点虽然没有有意义的函数值(非0/0型的)，但却有尽管是无意义的函数值0/0。于是其极限值也必为0/0(尽管也不是“有意义”的极限值)。况且按照不可达极限的定义，即使我们由于在0点有不合理的函数值0/0，因此强行“规定”在0点没有函数值(指有意义的、也就是分母不为0的)，即函数的定义域不包括△x=0点。但由不可达极限的定义，此时也完全不等于没有“不可达”意义上的极限0/0(尽管它是个不合理的极限值也罢)。显然，这里完全没有在△x=0点虽然没有有意义的函数值(此时函数值为无意义的0/0)，但却可有有意义的极限值(此时为1)的任何可能。

如此说来，有人也许会提出：那么，你论证了半天，究竟自函数的比值函数△x/△x还有没有导数？我们说，当然有。它就是△x/△x=1/1=1。分子分母相除得之。“1”这个函数就是△x/△x的导函数。即使在△x=0点它也是1。这里根本不用什么在0点的极限来得到它。因为由前文的论证，△x/△x在0点的有意义的极限是没有的(要有也是0/0)，用它求导当然不可能。但导数当然有，就是1。定义域包括△x=0点。也就是说，想通过极限来求导不可能，但这不是无导数或求不出导数。这是两回事。“1”这个“函数”在0点当然可以有极限而且是可达极限值(显然仍旧是1，与其在0点的函数值一致)，但不能说1这个函数也就是“导函数”是由函数△x/△x在0点的极限求出的。

二、 连续统、测度、点与时间、时刻、瞬时、速度、瞬时速度问题分析

笔者在文献2中，讨论了测度问题，而这个问题又直接与所谓“连续统”有直接关系。事实上，这两个概念在自然界或物理上的对应概念，就是时间。总在流逝的时间，就是物理化的连续统，而抽象的“时刻”、“瞬时”概念，就对应于抽象的“点”概念，无论是有理点还是无理点。点无体积、长度(也可以说长度为0)，因此距离不应是由无数个点所构成的(无数个0相加仍旧是0，不可能无中凭空生出有来)。同理，任何时间段也不是由无数个瞬时、时刻相加得到的。这是两个虽然有关、但截然不同的概念，一如尺子与尺子上的刻度的区别。不能说一把尺子是由尺子上的刻度相加组成的。有人又说可定义尺缩为0即为点。尺缩为0即尺子上的两个端点重合。我们总不能定义点为“二点重合或合为一点即为点”吧？此为循环定义。在如此认识下，本质上依赖于时间段的速度概念和依赖于长度的导数概念，在瞬时、时刻、点上，就没有原始定义，因为不满足速度、导数的原始定义中的必要条件，也就是分母上要出现不能为0的时间段或长度、距离等概念，而时刻、瞬时、点等概念的定义就是时间段或长度为0。一般而言，速度概念是或“折合成”单位时间段(也就是数量为“1”)物体所运动的距离(也许也可以不折合成“1”，称为“广义速度”，但不能为0)。一个比式，分母上的任何数值都可以“折合”成“1”，但唯独0不成。因此，在△x=0点，原始的有意义的速度进而导数概念是没有的，连0也不是(速度为0，意味着时间段不为0时运动距离为0，而非时段为0，运动距离的为0)，而是无意义的0/0。但我们不是总有瞬时速度和导数概念吗？如何解释呢？这实际是一个“次级定义的问题”：由于匀速运动任何时段的速度值都一样(分母折合成1时，分母值一样)，于是以每一个不同的时刻为起点的时段的速度值都一样，由此之故，我们定义这个速度就是该“时刻”的速度，也就是所谓“瞬时速度”。而曲线、变速运动中的瞬时速度，是该时刻(瞬时)一旦解除曲线、变速运动所必须依赖的受力时物体的匀速直线运动的速度。换言之，如果物体始终受力，哪怕涉及的时间段、距离再小甚至“无穷小”，其速度也是始终随不断变化、流逝的时间处于变化中的，而没有一个确定的“瞬时速度”。由此分析可以看出，如果不采取上述瞬时速度进而导数的定义(笔者以往论文中早有涉及)，就不可能消除其中的本质性矛盾，也就是贝克莱悖论。

此外，就算增量比值函数在自变量△x=0点存在极限(前已述及，这个极限实际不存在)，也是所谓“不可达极限”，即只可不断、无限接近，但不能真正到达的那种类型的极限。因此，以这样的“极限值”去定义瞬时速度，是会有问题的：时间流逝中的“时刻”、“瞬时”不但在现实中“可达”，而且必被越过，因此绝不是什么“不可达极限”可以定义的。而速度(即使是瞬时速度)的定义或本质，是单位时段运动的距离，显然，“单位时段”不可能是“0”，而是“1”。所谓“不可达极限”，按古语就是“日取其半，万世不竭”。而现实世界中的“时刻”、“瞬时”，绝对不可能是不可达的。如果取不到每一个瞬时，就不可能有时间的流逝。

三、 微分的定义问题

我们从微分的定义中，也可以看出端倪：如果微分是无穷小，但以极限论为基础的标准分析是排斥无穷小的，这点显然无法解释；如果微分是极限，我们说，导数、瞬时速度等概念之所以被标准分析看成或认为是有意义的极限值而非无意义的0/0，就是因为分子分母同时趋于0。如果没有这一点，无论距离还是时间，当然都可以单独去趋于0甚至等于0。但现在的“微分”与导数完全不同，不是个比值，需要单独定义，而且并不处于分母位置上，它再也不能被要求“不允许为0”了吧？于是，人们不得不将微分定义成与其名称完全不符的宏观量，所谓的函数的“线性主部”(如是次要部分，要它几乎就没有道理)，后来发现对有的函数而言还谈不上什么“主部”，所以干脆就定义成“线性部分”。但这一定义是只图眼前过关。它明显地与导数的定义不一致甚至矛盾，是一种回避以致掩盖矛盾(所谓“把污物扫到地毯下”)的做法。我们说，定义微分的目的是什么？是求积分。当我们求积分时，也还得回来要求每一个微分段无限趋于0，原来直接定义极限不成，做积分时却可以而且必须求极限，明显矛盾。

微分定义中另一个更明显的问题，就是广被诟病的自变量dx=△x的问题，也就是自变量的微分必须等于其自身的增量。如所周知，微分的一般定义是函数的“线性主部”，二者绝不相等。但自变量的微分却必须重新定义，这要求自变量不能再是任何变量的函数(只能是其自身的函数，否则将有dx(t)=△x(t)，明显违反微分定义。其中t为自变量x(此时已经是个函数了)的自变量)，甚至不能是其函数的函数，也就是y可以是x的函数，x却不能是y的函数。著名数学、逻辑学家莫绍揆早就指出了这方面的问题，其后不断有人也指出来，但始终未见任何有力的反驳意见。可见数学界对此实际上是无话可说的。这与导数问题不同，以往对微积分求导的极限法的任何质疑，往往都会引来不少反驳意见和表态。当然，微分问题只是表象，本质上还是导数问题。笔者以往文章对此早有讨论。

四、 ε-δ语言下的相关讨论

就是在所谓的严格的极限定义也就是ε-δ语言下，对于增量比值函数而言，也没有有意义的极限值。分析或证明如下：

在文献2的分析下，我们已知，文献2公式2的求极限公式，必须首先分子分母相除以“消去”分母可能等于或趋于0的自变量。而这关键的一步，却赋予了原先的极限式以新的内容，也就是所谓“分子分母相除”或“消去分母”，本质上等于把分母值“折合”成1。这是无可否认的事实，只不过通常为了简化，我们把这个分母上的“1”省略了而已。于是，当一个函数的分母上有自变量时，每有一个与在函数的分母上的自变量有关的正数δ，如果还都有一个与比值函数有关的正数ε，则其实应该严格地是ε/1，也就是分母被“折合”成了1，但显然仍旧应该是个比值，与原比值函数一致，而ε实际上是处在分子上的。也就是说，对增量比值函数这个特殊情况而言，仅就数值意义上，应该有ε=ε/1=θ/δ,这里θ为另一个与δ相关的正数(当然也是变量)。于是，当在比值函数分母上的δ→0时，我们还能得到ε吗？当然不能。只有在δ→1或δ=1时，我们才能得到ε/1=θ。而当δ→0时，我们只能得到θ→0，也就是最终得到“极限”0/0，更确切地说也就是没有有意义的极限。

总之，牛顿、莱布尼兹求导方法无意中以除法消去了增量比值函数分母上的自变量(文献2公式1)，如此，尽管始终没有被意识到，但它实际上做的是如文献2公式5(即本文公式6)所显示的，真正决定导数定义的曲线的割线上二点的横坐标差(也就是自变量值)就是1，而且自此始终为1；而纵坐标差中包含的自变量差(横坐标差)与横坐标差之比自然就始终保持是1/1(不十分严格地或数值上看就是1)，但绝对不可能再是0或什么趋于0(再一次强调：始终如此，割线变切线后也如此)。这是因为分子分母做除法在先，既然做了除法，被除数也就是分母就只能始终事实上为1了(当然可以不写，但此时省去或消去的只能是这个1，而绝非0)。至于此后分子上如果还有自变量△x，那也是割线方程中自变量的系数中所包含的(作为线性方程中自变量系数的一部分的)自变量，它的趋于0或等于0，与比值的性质无关，而只与比值的数值也就是斜率的数值(割线或切线的斜度)有关，因此也就没有曲线上二点趋于一点或干脆二点合一时的曲线的纵、横坐标差之比(产生贝克莱悖论的根源)的问题了。至于此后作为割线系数中的那个自变量△x的趋于0或实际就是等于0，已经与割线上的真正决定其斜率所必须的两点(两点间的增量或距离不能合为一点为0)无关了。此时剩下的那个系数中的自变量△x，只决定割线与曲线相交二点的不同位置及对其斜率的影响。曲线上的二点重合为一点(即自变量的增量为0时)，割线变切线。切线的斜率即导数。此导数明确为宏观量，既不是无穷小，也不是极限。至此，微积分贝克莱悖论问题，当可彻底澄清。极限法无必要，需要无穷小的非标准分析也无必要，而且本质上都是错的。但这绝对不是反对微积分，相反，正是使微积分返璞归真，重新回到本源的牛顿、莱布尼茨求导方法。只不过他们没有意识到用除法消去分母上的自变量究竟意味着什么，因此产生了贝克莱悖论。而由笔者前期系列论文及上文分析揭示，这个除法不是随便做的，它是有其意义的。在这个意义下，不但△x=0点的极限不存在了，而且贝克莱悖论也不存在了，所需要的只是对导数重新定义，就可以解释牛顿、莱布尼兹求导方法的合理性，因此无疑可以消除微积分已知和潜在矛盾、悖论，同时使微积分理论(包括导数和微分)不但更简单，同时当然更合理。

五、 作了除法后，究竟求出的是哪个函数的极限？

总之，作了除法后，在牛顿以及极限法那里，Δx/Δx消失不见了(实际只能是“1”或更严格的“1/1”)，这等于是先令Δx=1或趋于1，然后令原分子中剩下的的Δx又等于0或趋于0(其实都一样)，总共求了两次Δx的值或极限值。注意，这是牛顿法虽然没有意识到，但实质上所做的。可是以往理论却说这就是作为导数的原比式在分母上的Δx趋于0时的一次(注意，不是实际上的两次)极限值。而实际上除法做了后，Δx/Δx当然应该等于1/1，而它是分子分母上的自变量Δx相除(自除)等于1(或更严格地分子分母都等于1)得到的。因此，除非当自变量Δx趋于0时自变量Δx等于1或趋于1这个不可能存在的事发生，否则是得不到这个1/1的。所以才可说有意义的极限根本没有，是0/0。但如何解释牛顿法可以得到导数的正确结果？必须重新解释。也就是牛顿的实际做法中，由于无意中做了除法，实际已经把分子分母上有相比关系的Δx/Δx与其它的Δx区分开了。它的几何意义，就是割线上自变量增量△x=1的那一点。它不随割线沿曲线向切线运动而变化，更不会趋于0或等于0。但在这个运动中作为线性方程系数中的那个孤立的Δx是趋于并最终等于0的。必须要强调的是，函数1(就算其在Δx=0点无定义)与函数Δx/Δx有本质的不同。前者因为在做除法消去分母上的自变量之后实际是1/1,于是作为原函数(分子上)与自变量(分母上)不再受自变量Δx的任何影响，因此在坐标图上是一条平行于横轴的平行线；而Δx/Δx的原函数即作为分子的函数Δy=Δx随其自变量Δx(分母上的)的不同取值在坐标图上是一条45度角的斜线。而那个“水平线”取值(恒为1)实际与自变量Δx无关，就算我们把定义域“人为地”、“硬性地”限定为Δx≠0，也就是在0点函数无值、不等于1，但它(也就是函数1)其实是允许在0点可以有值1或极限1的，也就是“虽然被硬性规定了没有，但其实可以有”，因此做了补充定义后就可以有函数值、有极限1了。但Δx/Δx就不仅仅是在Δx=0点“被硬性地规定”无定义这么简单的问题了，它更进一步在该点是“不允许有定义”或“不允许再有定义”(即：“没有也不允许有”)同时也没有相应的极限。如果二者相除等于1，那实际就把函数改变成1而非原先的Δx/Δx，因此二者有本质的区别。况且极限法终难逃脱循环论证的窠臼：说必须自变量Δx不能等于0而只能趋于0才能做除法消去分母中的自变量Δx，可这个“趋于0”的极限，却又是只能由作了除法之后才能得到。在做除法“求出极限”之前，怎么就知道自变量不能为0但可以有极限0的？这个断语如何下的？还不是做了除法“之后”才声称求出了极限？可以看出，这个极限在Δx=0点根本就不存在。总之，求极限之前的除法消去分母上的Δx，等价于令Δx=1或者Δx→1，得到了另一个函数z=1，此时求其在Δx→0时的极限，等于对原函数Δx/Δx求了两次极限，第一次Δx→1，把一个在坐标系中的斜线变成了平行线；第二次Δx→0，把一个平行线再求极限。此时的极限，已经不是原先那个45度斜线的极限了。

参考文献：

[1]莫绍揆.试论微分的本质[J].南京大学学报(自然科学),1994,(03).

[2]沈卫国.论增量分析视野下的测度问题、微积分求导及连续统的可数性[J].前沿科学,2017,(03).

[3]方源,王元.微积分(上)[M].北京：高等教育出版社，2014.

[4]沈卫国.论微积分求导公式的一种全新推导模式(解方程法)及贝克莱悖论的彻底消除[J].天津职业院校联合学报,2013,(02).

[5]沈卫国.微积分核心概念的无矛盾表述——不需要无穷小、极限等概念的增量分析[J].天津职业院校联合学报，2015,(05).

[6]沈卫国.微积分核心概念的无矛盾表述(续)——不需要无穷小、极限等概念的增量分析[J].天津职业院校联合学报,2015,(11).

[7]沈卫国.微积分极限法(标准分析)的本质及问题详析[J].天津职业院校联合学报,2017,(06).