基于双谱分析的雷达有源欺骗干扰识别
,
(国防科技大学电子对抗学院,安徽 合肥 230037)
0 引言
随着电子技术的迅猛发展,电子干扰与抗干扰之间的博弈越来越激烈,电磁频谱权的争夺成为了现代电子战中决定胜负的关键,雷达对抗战也随之越来越重要。作为威胁跟踪雷达的三种主要的欺骗式干扰技术,距离拖引干扰(RGPO)、速度拖引干扰(VGPO)和距离-速度同步拖引干扰(R-VGPO)通过让雷达系统接收到虚假错误的目标和信息,致使雷达无法有效检测出真实目标及其参数,从而使雷达无法正常发挥作用。因此,开展针对三种欺骗干扰的识别算法已经成为雷达对抗领域研究的热点,具有广阔的前景与价值。
鉴于研究的内容涉及军事等敏感领域,国内外在欺骗式干扰识别方面的成果报道较少,特别是国外的研究成果,能够找到的资料有限。文献[1]结合小波变换理论,提出了基于小波变换后的高频细节分量能量比的干扰识别方法,该方法受噪声影响较大,在低信噪比下识别效果一般。文献[2]通过分析DRFM产生的RGPO干扰受到DRFM相位量化失真的影响,引入信号锥理论建立检测模型,采用通用似然比检测器实现对RGPO干扰的识别。文献[3]在文献[2]的基础上进行完善,研究了真实回波和干扰同时存在情况下的检测。但是文献[3]和文献[2]的算法在相位量化位数大于4时失效,使用范围较窄。文献[4]从三种拖引干扰的二维分布特性的差异性出发,提出了基于积谱矩阵的局部二值模式识别方法。但此方法处理数据维数较大,处理速度偏慢。李建勋[5]等人根据干扰的双谱分布提出了基于双谱特征和模式识别的方法。但该算法仅提取了双谱的局部特性,整体特性没有被有效的利用。本文针对上述问题,提出了基于双谱分析的雷达有源欺骗干扰识别算法。
1 基于双谱分析的干扰识别算法基本理论
1.1 欺骗式干扰信号模型
欺骗干扰指的是通过发射或转发具有欺骗性信息的信号,扰乱或者迷惑雷达,使其不能正确的检测真正的目标或者目标参数[6]。本文以线性调频信号(LFM)为例,主要针对距离拖引干扰、速度拖引干扰以及距离速度同步拖引干扰的检测与识别。这三种干扰的实施一般经过捕获期、拖引期以及停拖期,本文主要针对拖引期的某一脉冲信号进行分析。
雷达发射信号为LFM,则其可以表示为:
S(t)=exp[φ(t)+jφ0]
(1)
式中,φ(t)=jπ(2f0t+kt2),f0为中频频率,k为调频斜率,φ0为发射信号的初始相位,假如与雷达相距R0的位置处有一个目标,则此时雷达接收机接收到的真实信号为:
ST(t)=KT·exp[φ(t-tr)+jφ0]
(2)
当DRFM干扰机实施RGPO干扰时,由于产生的干扰具有相干性,则在雷达波束内同时存在目标回波和RGPO干扰,两种信号发生相干合成,则雷达接收机接收到的合成信号为:
JR(t)=KT·exp[φ(t-tr)+jφ0]+
KR·exp[φ(t-tr-ΔτJ(t)-Δt)+jφJ]
(3)
式中,KR为RGPO干扰的幅度,Δt为DRFM干扰机从信号接收到转发的固有时延,φJ为干扰信号的初始相位,ΔτJ(t)为调制函数,在这里本文选取的调制函数为ΔτJ(t)=kt。
当DRFM干扰机实施VGPO干扰时,由于产生的干扰具有相干性,则在雷达波束内同时存在目标回波和VGPO干扰,两种信号发生相干合成,则雷达接收机接收到的合成信号为:
JV=KT·exp[φ(t-tr)+jφ0]+KV·
exp[φ(t-tr-Δt)+jφJ]·exp(2jπΔfd(t))
(4)
式中,KV为VGPO干扰的幅值,Δfd(t)为多普勒频移。
当DRFM干扰机实施R-VGPO干扰时,则雷达接收机接收到的合成信号为
JRV=KT·exp[φ(t-tr)+jφ0]+
KRV·exp[φ(t-tr-ΔτJ(t)-
Δt)+jφJ]·exp(j2πΔfd(t))
(5)
式中,KRV为R-VGPO干扰的幅值。ΔτJ(t)和Δfd(t)满足。
1.2 双谱分析的基本理论
双谱的定义为三阶累积量的二维离散时间傅里叶变换。用公式表示如下:
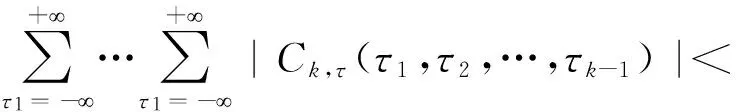
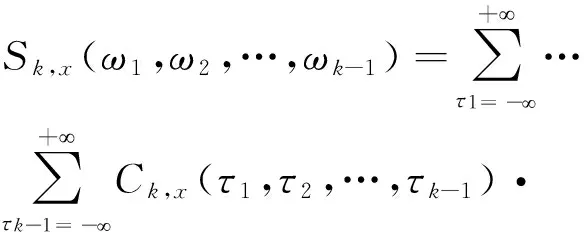
(6)
当k=3时,三阶谱即为双谱,通常用Bx(ω1,ω2)表示,则

(7)
2 干扰特征识别算法
由于DRFM可以产生高保真的相干干扰,所以根据雷达是否受到欺骗干扰以及具体的某一干扰,雷达接收信号存在下面四种情况。
(8)
其中,ST(t)代表目标回波,JR(t)代表干扰机实施RGPO欺骗式干扰时的雷达接收信号,JV(t)代表干扰机实施VGPO干扰时的雷达接收信号,JRV(t)代表干扰机实施R-VGPO干扰时的雷达接收信号,n(t)代表高斯白噪声。这四种情况在时域、频域上均存在微小差异。传统的时域或频域分析方法只能够获取信号在时域或频域的局部特性,获得的信息并不完整。高阶谱方法能够抑制高斯噪声干扰,同时能够保留信号的幅度和相位信息,在多个领域有着广泛使用,尤其以双谱应用最为广泛。本节针对这四类情况对雷达接收信号双谱估计得到的三维双谱信息进行比较,经过降维和归一化处理后,对得到的二维特征谱进行特征提取,最后通过分类器进行干扰的识别。其分类识别系统流程如图1所示。
图1 欺骗式干扰识别框图
Fig.1 Diagram of deception jamming identification
2.1 双谱分析原理
对于雷达接收信号,双谱分析不仅能够抑制接收信号的高斯噪声干扰,而且可以很好的描述和检测接收信号的非线性特征。虽然欺骗式干扰不是平稳随机过程,以RGPO为例,JR(t)=ST(t)+JRGPO,其中
JRGPO=KReφ(t-tr-ΔtJ)+jφ0=
KRejπ2f0(t-tr-ΔtJ)+k(t-tr-ΔtJ)2·ejφ0=
KRejπ-2f0ΔtJ+kΔtJ2-2k(t-tr)ΔtJ·
ejφ0·ejπ2f0(t-tr)+k(t-tr)2=
KRGPO·ejπ2f0(t-tr)+k(t-tr)2
(9)
所以其均值为KRGPO,由于单一脉冲脉宽很小,所以其自相关函数只与时间差有关,对于拖引期的某一脉冲信号来说是广义平稳随机过程。
考虑到这一特点,本文针对拖引期某一脉冲信号x(i)进行分析研究。实际应用中,参量模型法和非参量法是两种信号双谱估计方法,其中,非参量法包含间接法和直接法。本文采用间接法进行双谱估计[7]。具体的步骤如下:
1)将长度为N的观测数据等分为K段,每段数据含有M个点。
2)将第n段数据设为x(n)(0),x(n)(1),…,x(n)(M-1),分别计算每段数据的三阶累计量的估计值:
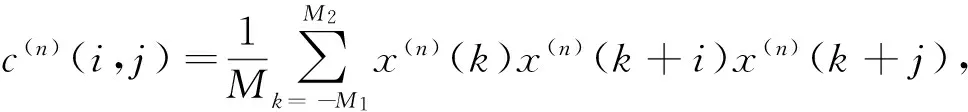
(10)
其中,M1=max(0,-i,-j),M2=min(M-1,M-1-i,M-1-j)。
3)将每段求得的三阶累计量进行统计平均,得到的结果即为该数据的三阶累计量。表示为:
(11)
则双谱估计为:
(12)
其中,L ①ω(m,n)=ω(n,m)=ω(-m,n-m)=ω(m-n,-n) ③ω(0,0)=1 ④W(ω1,ω2)≥0,∀(ω1,ω2) 图 2为在信噪比SNR=4 dB,干信比JSR=5 dB下的四种情况的雷达接收信号的双谱分析结果。从图中可以看出四种情况下的雷达接收信号的双谱估计均存在明显的差异,可以通过双谱估计提取特征。 利用上图结果直接作为特征进行干扰识别会因为特征维数的因素导致计算量偏大。增加识别的时间。因此,为了减少计算量和识别时间,需要对四种情况下的雷达接收信号的双谱特征进行降维。为了尽可能的保留四种情况下的雷达接收信号双谱估计的差异特征,本文将得到的三维双谱沿Y轴垂直投影到XOZ平面[8]。 (13) 同时由于四种情况下雷达接收信号双谱分析的幅度不同,不利于比较和分析,所以对幅度进行归一化处理。图3分别为四种情况下雷达接收信号双谱估计降维后的特征曲线。 对图3进行观察可以发现,四种情况下的雷达接收信号均有自己独特的二维双谱特征谱,可以作为干扰识别的特征。但是直接根据特征曲线判断干扰的类型计算量仍然过大,因此需要进一步对降维后的二维特征曲线提取特征参数。 从上图可以看出四种情况下雷达接收信号双谱估计降维后的特征谱均有自己独特的几何形状和复杂程度。盒维数和熵特征能够很好的描述特征谱的复杂程度和不确定性。所以本文采用提取降维后的二维特征谱的盒维数、瑞利熵以及指数熵组成特征向量,最后通过分类器进行识别。 2.3.1盒维数特征提取 作为分形理论最主要的参数,分形维数能够很好的描述分形集的复杂程度[9]。作为分形维数最基本的一种,盒维数定义如下: 假定(X,d)表示为一个度量空间,H表示为X的一个非空紧集族,令X表示为一个非负实数,B(x,ε)表示一个以x为中心,半径为ε的闭球。令A为X的一个非空紧集,对于所有正数ε,用N(A,ε)表示覆盖A的最小闭球数,即: (14) 其中,x1,x2,…,xM代表非负实数X不同的点,令A是非负的紧集,若满足: (15) 则DB称为紧集A的分形盒维数,表示为DB=DB(A)。在实际求解盒维数的过程中能够进行简化,其过程如下: 首先将二维特征序列g(i),u=1,2,…,N放置在单位正方形内,如果横坐标的最小间隔为q=1/N,假定N(q)为下式所示: (16) 则盒维数用计算式表示为: (17) 2.3.2Renyi熵特征提取 熵用来描述信息的不确定度。雷达接收信号是由有用信号与噪声相叠加构成,有一定不确定性[10],并且与信噪比的值有关,可用熵进行表示。 Renyi熵作为香农熵的延伸,可以作为信源复杂度以及信息量的测量[11]。其用公式表示为: (18) 其中,α表示Renyi熵的阶数,当α=1时,Renyi熵等价于香农熵。在此,将双谱估计降维后的特征谱看成二维随机变量的概率密度[12],则双谱估计经过降维处理后的特征谱的指数熵可以表示为: (19) 2.3.3指数熵特征提取 为了有效解决香农熵在实际问题中存在的缺陷,满足实际需要,指数熵的概念应运而生[13]。假设情况i(i=1,2,…,n)出现的概率为pi,则p(t)在状态t下指数熵的定义为: (20) 将双谱估计降维后的特征谱可以看成二维随机变量的概率密度[12],则双谱估计经过降维处理后的二维特征谱的指数熵可以表示为: (21) 其中,N为二维特征谱的运算结果总数。经过反复实验和综合考虑,本文采用盒维数、指数熵、Renyi熵组成特征参数集。具体的识别算法如图 4所示。 实验中采用RGPO,VGPO,R-VGPO三种拖引期干扰下的接收信号,设置仿真参数如下: 跟踪雷达发射波形为LFM,信号带宽5 MHz,脉宽10 μs,采样频率20 MHz;干扰机固有时延150 ns;距离拖引的拖引速度取750 m/s;速度拖引的拖引速度50 kHz/s;接收信号的信噪比从0 dB到15 dB每隔1 dB递增,JSR=5 dB,在每种信噪比条件下进行600次Monte Carlo实验。根据2.3节提取二维特征谱的盒维数、指数熵、Renyi熵作为特征参数,并求取平均值。仿真结果如图5所示。 图5为对降维后的二维特征谱进行特征提取后的特征参数随信噪比的变化曲线。从图5(b)可以看出,S3(VGPO)情况下提取的Renyi熵与其他三种情况特征差异较大,能够很好的进行区分。当SNR≥3 dB时,S4(R-VGPO)情况下的提取的Renyi熵与其他三种情况特征差异较大,能够很好的进行区分,但是在低信噪比的情况下不能很好的区分。图5(c)中能够看出,当SNR≤3 dB时,S4(R-VGPO)情况下提取的指数熵正好能够进行区分,实现对图5(b)的互补。图5(a)能够将剩下的两种情况即S1(目标回波)和S2(RGPO)进行区分。因此,将提取出的三种特征联合起来组成特征向量。 本文利用Monte Carlo实验产生的600个独立样本,四种情况下共2 400个信号放入分类器中,其中前1 200个信号为训练集,后1 200个作为测试集,由于支持向量机对于小样本的分类具有很大优势,分类器选用v-SVC,核函数为RBF。每个信号都按照前文的方法依次进行双谱估计,降维产生二维特征谱,特征提取,将提取的特征向量输入到分类器进行分类识别。仿真结果如下所示,从图中可以看出,随着信噪比的提高,这三种干扰的识别性能得到提升,在SNR=4 dB时,三种干扰的识别率均大于90%,在SNR=6 dB时,三种干扰的识别率均接近100%,该算法对于三种干扰识别的效果都比较好。 将本文结果分别与文献[1]和文献[4]作比较,图 7为3种特征提取方法识别效果图,从上图中可以发现本文的识别率受信噪比的影响最小,并且在识别率上效果最好,特别是信噪比SNR≤6 dB时,识别率较文献[4]和文献[1]有较大提高,文献[1]在SNR<4 dB时效果好于文献[4],在SNR≥4 dB时效果差于文献[4]。实验可以证明该方法的优越性。证明基于双谱估计的方法对雷达欺骗干扰信号进行分类识别是可行性。 本文提出了基于双谱特征的雷达欺骗干扰识别算法,该算法对受到干扰与否的四种情况下的雷达接收信号进行双谱分析,经过降维和归一化处理后,将三维双谱信息转化为二维特征信息,对得到的二维特征谱提取熵特征和盒维数组成特征参数集放入分类器中进行分类识别。仿真实验表明,该算法具有有效性和稳定性,为后续抗干扰措施的选取提供了先验信息。但本文仅仅考虑噪声对算法的影响,下一步需要对复杂电磁环境下的干扰识别算法进行深入的研究。 参考文献: [1]田晓,唐斌.基于归一化小波分解能量比的雷达有源欺骗干扰识别[J].数据采集与处理,2013,07(04):416-420. [2]Greco M,Gini F,Farina A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Transactions on Signal Processing,2008,56(5):1984-1993. [3]刘兴华,罗景青,王文涛.相位量化DRFM欺骗干扰的自适应检测[J]. 数据采集与处理,2015,30(06):1302-1309. [4]李艳莉,田晓.基于积谱矩阵局部二值模式的欺骗干扰识别[J]. 电讯技术, 2015(4): 441-446. [5]李建勋, 秦江敏,马晓岩. Kohonen网络用于雷达抗速度欺骗干扰中的特征提取[J]. 雷达科学与技术, 2004,02(2): 82-86. [6]张永顺,童宁宁,赵国庆.雷达电子战原理[M].北京:国防工业出版社,2010. [7]张贤达.现代信号处理[M].北京:清华大学出版社. 2002:278-280. [8]杨少奇,田波,周瑞钊.应用双谱分析和分形维数的雷达欺骗干扰识别[J].西安交通大学学报,2016,50(12):128-135. [9]Du J X,ZHAI C M,Wang Q P. Recognition of plant leaf image based on fractal dimension features[J]. Neurcomputing,2013,116:150-156. [10]张葛祥,胡来招,金炜东.基于熵特征的雷达信号识别[J].电波科学学报,2005,20(4):440-445. [11]白航,赵拥军,沈伟,等.基于时频分布Renyi熵特征的雷达辐射源识别[J].电路与系统学报,2013,18(1):437-442. [12]李建勋,唐斌,吕强.双谱特征提取在欺骗式干扰方式识别中的应用[J].电子科技大学学报,2009,38(3):329-332. [13]周林,刘先省.基于新定义信息熵的目标检测算法[J].信息与控制,2005,34(1):119-122.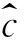
2.2 二维特征谱曲线的生成
2.3 二维特征谱的特征提取

3 仿真实验及结果分析
4 结论

