基于正交试验设计的计转数定距弹数据处理方法
,, ,
(陆军工程大学石家庄校区,河北 石家庄 050003)
0 引言
利用计转数原理实现精确定距空炸是近年来提出的新的定距原理,具有可靠性高、结构简单和定距精度高等优点[1]。根据地磁感应原理,利用安装于引信的地磁感应传感器实现精确定距是重要的定距手段[2-4]。丁立波等[5]提出了基于计转数原理的自适应炸点控制技术,进一步提高精确定距起爆的精度;朱炜等[6]提出了计转数计时的电子时间引信技术,有效提高了弹药对目标的毁伤能力,使得计转数技术不断得到完善。
从理论上分析可知,弹丸出炮口后每转一周前进的行程是一定的,且与初速无关,而实际上每发弹丸初速不同、射程不同以及射角不同都会使其遇到的阻尼不同[7],这些因素使得弹丸具有不同的弹道,严重影响弹丸的定距精度。然而,定距精度是对来袭导弹实施“弹幕”式拦截和小口径高炮实现防空反导的保证,为了提高定距精度,必须对影响定距精度的因子进行分析和修正,马少杰等[8]将定距空炸精度误差进行分类,并提出利用初速修正起爆时间;冯德朝等[9]研究了自然风对旋转弹丸外弹道性能的影响,确定了风对弹丸飞行过程的影响方式,有利于后期弹丸的进一步修正。在射击过程中满足修正条件,定距空炸精度会得到很大的提高,但是在实战条件下,由于对武器系统迅速反应的要求以及外弹道本身的复杂性,不可能将所有影响外弹道变化的因素都加以修正。因此,必须对影响计转数弹丸定距精度的因素进行综合分析,在在弹道修正过程中对不同影响程度的因素进行取舍。针对这一问题,本文利用正交试验设计,对影响弹丸转数的部分因素进行仿真计算,综合分析弹道参数变化对定距精度的影响,并确定弹道参数变化的相对影响程度,为计转数弹丸定距精度研究提供参考。
1 正交试验设计
1.1 正交试验设计的基本思想
在实际问题中,与随机变量有关的因子数往往很多,在进行全因子分析时,随着因子数的增加,分析的次数将成倍增加。例如,某个随机变量的取值可能与3个因子有关,每个因子又有3个水平,因此要探究每个水平的因子对试验结果的影响就需要做至少27次试验。在进行分析时,对每个因子的每一种水平组合,都要进行试验,称为全面试验设计[10]。正交试验设计可得到全面试验设计所需要的试验结果,而只选出一部分组合来做实验,可减少试验次数,提高试验效率,在生产实践中被证明是一种十分有效的试验方法。
1.2 正交表的设计
正交表是正交设计的工具,试验安排及对试验的结果分析均在正交表上进行。常见的正交表有L4(23)、L8(27)、L9(34)、L27(313)、L16(45)等。
下面以L9(34)以为例来说明正交表的正交性。L9(34)中,9表示试验次数,即表中的行数;3表示水平数;4表示列数,即此表能容纳的最大因素数。L9(34)是一张因素个数不超过4、所有因素均为3个水平的标准正交表。如表1所示,数码1,2,3分别表示第一、第二和第三个水平。
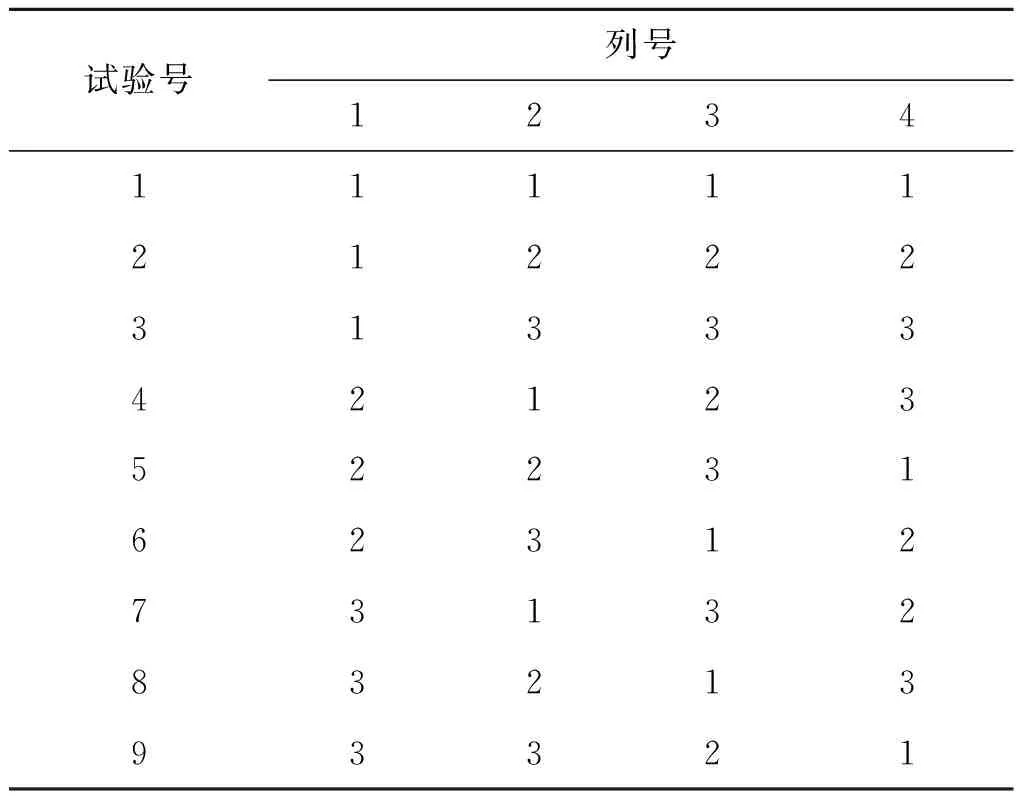
表1 L9(34)标准正交表Tab.1 Orthogonal test table
正交表的正交性体现在以下两个方面:
1)表中的任意一列中不同数码出现的次数相同,即各因素中的每一个水平在所有试验中出现的次数相同。
2)表的任意两列,若把横向的两个数码看成有序数对,则可能出现的数对均出现,并且出现的次数相同。
正交表的正交性表明,表中的各列地位平等,各列的搭配是均衡的。
正交试验设计的基本步骤如下:
1)明确试验目的,确定正确的试验指标。
2)确定因素、制定水平。确定影响试验结果指标的因素,要求这些因素都是可控的,否则无法观测到因素对指标的影响。每个因素选择a个水平,水平数可相等,也可不等。
3)根据前两个步骤,选择合适的正交表,进行表头设计。若试验中每个因素的水平数都是a,就选定Ln(am),其中m不小于试验要求的因素数。选定正交表后,将各因素分别填写在所选正交表的上方与列号相应的位置,一个因素占一列,不同因素不同列即进行表头设计。在选用正交表时,表中的列数不小于因素的个数,因此可能出现空列。
4)按设计方案进行试验并记录试验结果,以备分析。把表头上各因素的水平任意给一个水平号,并将各因素的诸水平所表示的实际状态或条件填入正交表中,正交表的每一行就代表一个试验方案。按正交表安排试验,记录各次试验结果并依次记于最后一列,利用数据进行结果分析。
1.3 正交试验设计的结果分析
为充分利用试验数据提供的信息,利用方差分析法对试验数据进行分析处理。
离差平方和的分解及自由度的计算:设试验次数为n,记第i次试验结果为Yi(i=1,2,…,n),则总平均为:
(1)
总离差平方和为:
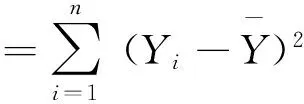
(2)
将S总分解成正交表各列的离差平方和(列数为n-1)
S总=S1+S2+S3+…+Sn-1
(3)
其中,
(4)
式中,a为水平数,r为个水平的重复次数,Kkj为第j个因素的第k个水平对应的试验数据之和。S总的自由度f总=n-1 ,即总试验次数减1。Sj的自由度fj=a-1,其中j=1,2,3,…,n-1。
每个元素各占一列,该列的离差平方和及其自由度就是该因素的离差平方和及其自由度。可用各因素对应列的离差平方和的大小来排定影响因素的次序。
2 计转数定距弹的数据处理方法
根据计转数定距弹的特点,在研究影响其定距精度的影响因子时,主要是获取单个因子变化时的有关数据,进行数据分析时,采用的是单个因子分析的方法。建立刚体外弹道模型,控制单个因子的变化,获取一系列数据,将获取的数据以表格、图像等形式呈现出来,通过对比观察,判断单个因子的影响程度。
方差分析是利用试验数据提供的信息,对试验误差进行分析,通过对获取的数据进行处理,计算出因子对所选参考指标的影响,最终的计算结果反映了各个因子所起的作用。方差分析是基于以下公式进行计算的:
(5)
式中, SST=SSA+SSE。第一式为总离差平方和,反映了全部观测值离散程度的总规模;第二式为水平项离差平方和,反映了各水平均值之间离散程度的规模;第三式为误差项离差平方和,反映了各个水平内部观察值离散程度的规模;第四式和第五式为对应的均方值,根据均值比服从F的特性,构造统计量进行离差平方和的比较,就可以确定单个因子的影响程度。对于试验值x,可以分成k个水平,其中第j(j=1,2,3,…,k)个水平的试验结果个数为nj,总的试验个数为n,利用方差分析法对试验值x进行计算,通过对计算结果的分析可以研究自变量(因子)与因变量(随机变量)之间的相关关系,分析出组间水平因子以及同一组内试验误差所引起的波动,鉴别各个因子的影响程度。
计转数定距弹的空炸精度受到多重因素的影响,为了达到方差分析的效果,确定主次因素的顺序,针对多因子多水平分析,提出了基于正交试验设计的数据处理方法对计转数定距弹的影响因子进行分析。在应用该数据处理方法时主要基于图1所示流程。
这种数据处理方法摆脱了仅仅局限于分析单个影响因子的弊端,是鉴别多个因子影响程度的有效方法。利用这种方法可有效的减少试验次数,迅速获得可靠的、有代表性的试验结果,并通过对试验结果进行计算,综合分析,利用数据来判断多个因子的相对影响程度。
3 试验设计与结果分析
3.1 试验设计
不同弹道参数变化会直接影响到定距弹的控制精度,为此,需要在不同环境下对弹道参数进行修正,但恶劣环境致使弹道修正系数不能全部满足条件,因此,必须舍弃相对不重要的影响因素。一般情况下,射距越大弹丸定距的精度就越低,随着距离的增加,不确定因素会进一步增多,从而不稳定性会进一步加大,因此弹丸在飞行过程中所累积的干扰会产生重要的影响。在计转数定距弹理论中,弹丸旋转一周前进的行程是一定的,与初速无关,但实际上每发炮弹初速不同,弹丸旋转的角速度变化就不同,从而对弹丸计转数产生影响。横风对角速度衰减影响较小,但纵风影响较大,因此必须根据当地实际情况进行弹道系数的修正。另外,在进行射击时空气密度和环境温度会对空中飞行的弹丸产生摩擦阻力,这就涉及到空气阻力系数选取的问题。因此,选取射距、初速、纵风和空气阻力系数四个因素为研究对象,每个元素选取三个水平,以此为例进行数值计算和分析探究。选取L9(34)正交表进行试验设计,如表2所示。
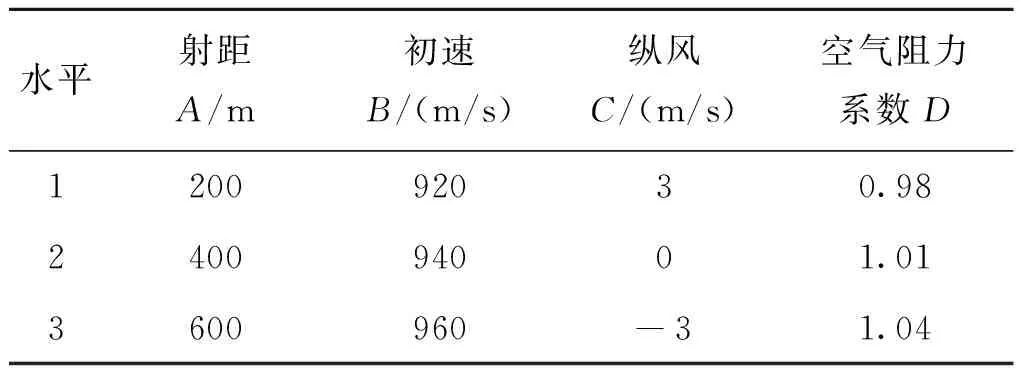
表2 元素和水平选取Tab.2 Selection of Elements and Standards
在射距选取上,以1 000 m内的短程射距为主,防止因射距过大所造成的误差掩盖了其他影响因子对精度控制的影响。在初速选取上,以普通弹丸的炮口速度为研究对象,可使研究具有普遍性。在纵风选取上,选取顺弹轴方向和逆弹轴方向进行对比,同时设置理想弹道即纵风为零,并将三者进行对比,可得出不同的纵风对控制精度所产生的影响。在空气阻力系数选取上,选取常规条件下的一般数值进行计算分析。仿真数据的选择尽量满足普遍性原则。
3.2 试验结果处理与分析
仿真实验是基于六自由度刚体弹道方程,利用气动参数建立弹丸六自由度刚体弹道模型,利用该弹道模型设计相关弹丸弹道参数,获取仿真数据。本文中将误差百分比定义如式(6)。

(6)
式中,实际转数是仿真实验得出的结果,标准转数是标准弹道环境下的的理想试验结果。利用公式(4)计算各因素水平的方差,计算结果如表3、表4所示。

表3 误差百分比计算Tab.3 Calculation of error percentage
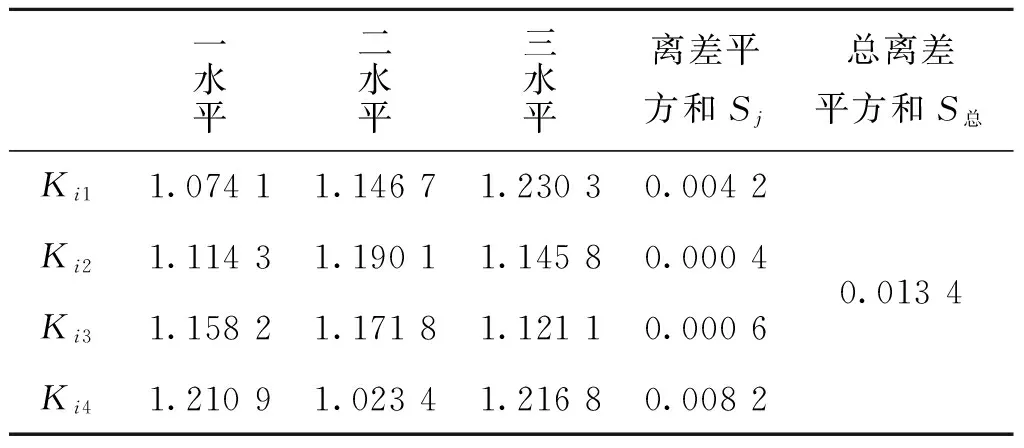
表4 各元素水平的方差Tab.4 Table variance of every element
由表3的计算结果可知,计转数定距弹具有较高的定距精度。分析表4可知,离差平方和S4>S1>S3>S2,即四个因素对计转数定距精度的影响大小排序为:4(空气阻力系数)>1(射距)>3(纵风)>2(初速)。从数值结果可以看出,初速变化对计转数定距引起的精确定距精度影响最小,主要是初速与转速成正比所致。由于弹丸出炮口以后不确定性增加,环境因素实时变化,使调整好的空气阻力系数的误差不断增大,严重影响计转数定距弹的控制精度。纵风将影响空气与炮弹的相对速度,影响飞行阻力,从而影响相同飞行距离下的时间、转数,在一定程度上影响对计转数定距弹的精度控制,且影响程度随射程的增大而增大。
4 结论
本文提出了基于正交试验设计的计转数定距弹数据处理方法,对影响定距弹精确空炸精度的影响因素进行综合处理分析。该方法对影响计转数定距弹精确空炸精度的因素进行综合处理分析,减少了试验次数,确定了影响因素的相对重要程度。仿真实验表明:
1)在所选择的因素研究中,初速对定距精度的影响最小,采用计转数方式定距,炸点位置和炸点预期非常接近,符合计转数定距弹基本不受初速影响的结论,进一步彰显了计转数定距弹的优势。
2)在四个研究因素当中,空气阻力修正系数对弹丸转数的影响最大。弹丸的射程不同,射角不同,以及弹丸在空中飞行过程中气温、气压、纵风等环境因素的实时变化,都将对空气阻力产生影响。
3)根据各影响因素可能产生误差的大小采取相应措施,才能保证计转数定距弹炸点控制达到预期作战目标。在恶劣的环境条件下进行实弹射击时,如果无法全部满足本文中四个因素的修正系数,可以按照空气阻力系数、射距、纵风和初速的顺序优先满足前者。
参考文献:
[1]李炜昕,张合,丁立波. 基于记转数测速的定距修正系统[J]. 测试技术学报, 2013, 27(2): 104-108.
[2] 常树茂,王利,弓楠. 基于地磁传感器的弹丸转数测试[J]. 弹箭与制导学报, 2011, 31(5): 200-206.
[3] 赵捍东,张亚,陈宏伟. 用地磁感应转数传感器实现引信定距方法的研究[J]. 探测与控制学报,2002, 24(1): 57-60.
[4] 张树霞,赵捍东,王占坡,等. 基于计转数定局技术和导程的弹道工程算法[J].中北大学学报(自然科学版), 2012, 33(6): 699-703.
[5] 丁立波,张合,马少杰. 计转数空炸引信自适应炸点控制技术[J]. 南京理工大学学报, 2011, 35(5): 600-603.
[6]朱炜. 基于计转数计时的电子时间引信技术[D]. 南京:南京理工大学, 2007.
[7]侯建,张方方.非标准条件下旋转弹丸刚体外弹道的建模与仿真 [J]. 海军工程大学学报, 2012, 24(5): 65-69.
[8]马少杰,张合.空炸引信定距误差分类即修正策略[J].弹道学报,2008,20(3):14-17.
[9]冯德朝,张方方,胡春晓.自然风对旋转弹丸外弹道性能影响的仿真研究[J].指挥控制与仿真,2012,34(01):96-98.
[10]李忠范,高文森. 应用数理统计[M]. 北京: 高等教育出版社, 2009.

