基于改进的正则化子空间追踪算法的ISAR成像

,,

(大连大学信息工程学院，辽宁 大连 116622)

0 引言

逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)具有全天时远距离目标成像的优势，已被广泛应用于军事及民用等领域[1]。传统的FFT成像方法，成像分辨率受发射信号带宽和目标转角的限制[2]，而发射大带宽信号以及增加相干处理时间会产生庞大的数据，对雷达系统的A/D转换速率、数据传输及存储等有较高的要求[3]。因此，有必要研究一种以较少的观测样本实现高精度ISAR成像的算法。

近年来发展迅速的压缩感知(Compressive Sensing, CS)理论[4]指出，当信号或信号在某个变换域是稀疏的，就可通过求解一个最优化问题，以少量的信号测量值通过稀疏恢复算法高概率的恢复出原始信号。而对于ISAR成像而言，目标回波由目标上所有散射点回波叠加而成[5]，其中强散射点起主导作用，其数目远小于回波采样点数，满足稀疏信号的特征[6]，因此可以将CS应用于ISAR成像领域，缓解传统成像方法带来的超大数据采集、存储和传输压力。

将CS理论应用于ISAR成像[7]的关键在于根据具体情况选择或设计一种快速有效的重构算法实现对原始信号的精确重构。近年来众多的综述类文章都对稀疏重构算法进行了归纳和分类[8]。凸优化和贪婪追踪算法是目前被广泛使用的两类算法。凸优化算法重构精度高，但计算比较复杂；相比之下，贪婪类算法在重构精度和计算量之间取得了较好的平衡，迅速成为研究的热点之一[9]。贪婪类算法的代表性算法为正交匹配追踪算法(OMP)[10]。目前大多数的贪婪类算法都是对OMP算法加以改进，以提高算法的重构精度与计算效率。例如StOMP算法是对原子识别步骤的改进[11]，而SP[12]和CoSaMp[13]等算法则是在原子识别步骤改进的基础上，增加了冗余原子修剪的步骤，来递归的进行重构支撑集选择。对于雷达信号而言，由于不同目标散射点的散射强度不同，故信号幅度往往是随机起伏的，对于这一类信号，若直接使用上述的OMP或SP等算法进行重构，则会产生两类重构错误问题：一类是幅度相对小的信号分量不能被正确重构；第二类是幅度相对较大的信号附近会产生“虚假”重构信号[14]。产生这种现象的原因在于感知阶段无法选出正确的原子，或是选出的原子不能很好地表达原信号，最终导致重构失败[15]。基于此，本文提出基于改进的正则化子空间追踪算法(MRSP)的ISAR成像方法。

1 压缩感知ISAR成像模型

ISAR成像实质上是用成像算法将回波中包含的散射点的位置和强度以图像的方式表示。若雷达与目标间平动分量已经被补偿掉，则ISAR目标成像等效为转台模型[16]。假设雷达发射线性调频信号：

(1)

其中，tr是快时间，fc是载频，γ是调频率，Tp是脉冲宽度。距离脉冲压缩后，忽略二次项与常数相位项，则目标上某散射点p(xp,yp)的回波信号表达式近似为：

(2)

其中，A表示回波信号幅度，Ta为观测时间，λ为波长，c为光速。假设观测时间内目标转角较小，则R(tm)≈R0+yp+xpωtm，R0为雷达与目标基准点的距离。根据式(2)所示脉冲压缩后的信号，假设某距离单元包含K个较强的散射点，并考虑加性噪声，则此单元的回波信号表示为：

(3)

其中，Bk和fk分别表示第k个散射点的散射系数和多普勒频率。

ISAR数据中的强散射点数相对于全部数据来说具有稀疏特性，因此原始数据图像可以通过CS技术进行感知重构[17]。定义时间向量t=[1∶N]TΔt，N=Ta/Δt为脉冲数量，Δt=1/fr表示时间分辨率，fr为脉冲重复频率。定义多普勒频域的频率分辨率为Δf，因此，离散的多普勒向量可以定义为fd=1：NTΔf。因此，构建一个傅里叶基为：

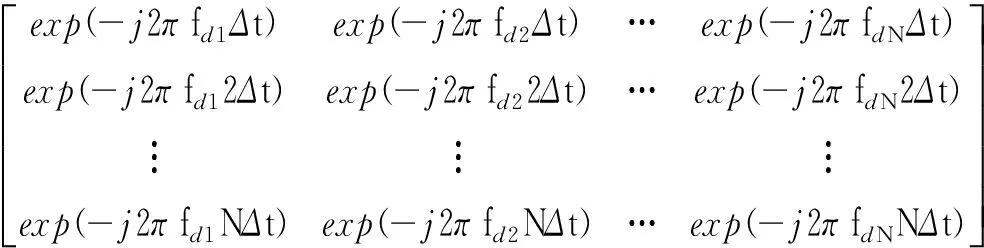
此时，将式(3)某个距离单元的回波信号写成矩阵形式为：

s=Ψα+n

(4)

其中，α为信号s在Ψ域的稀疏表示向量，其非零分量对应于K个最大散射点的复幅度。

在基于压缩感知的ISAR数据成像中，测量矩阵Φ∈RM×N(M

y=ΦΨα+n′=Θα+n′

(5)

考虑加性噪声，ISAR信号重构优化问题可以写为：

(6)

式中，ε为噪声门限，Θ=φΨ为感知矩阵。如何设计有效的重构算法重构式(6)，避免重构错误问题，提高重构效率是本文的主要目的。

2 基于改进的正则化子空间追踪算法的ISAR成像

2.1 改进的正则化子空间追踪算法(MRSP)

OMP算法作为最早的贪婪算法之一，其对于之后的各种改良算法和新提出的算法都具有重要的指导意义。从现有的研究结果来看，对OMP计算量的改善通常以损失些许重构性能为代价，而性能的改善则以较高的运算量或存储量为成本[18]。对比之下，SP算法具有较好的计算速度和重构概率，但是SP算法在每次回溯时，强信号分量总是得到保留，以至于在后续的回溯中，强信号分量遮挡弱信号分量，出现重构错误现象[14]。考虑实际应用，本文提出MRSP算法，采用黄金比例分割法(0.618法)[19]确定正则化过程实现支撑集的二次筛选，以及回溯反馈的思路来更加准确地估计、扩充目标信号的真实支撑域，最终重构出稀疏信号，使得压缩感知重构算法更具实用性。

MRSP算法在每次迭代过程中，首先计算残差r，然后求残差与感知矩阵Θ中各个原子(本文所提“原子”指组成感知矩阵Θ的各个列向量)之间的相关系数u，从u中挑选出绝对值最大的K(K为信号的稀疏度)个原子的索引值存入索引集J，然后采用正则化过程继续筛选原子，根据式0.618|u(i)|≤|u(j)|，i，j∈J，将J中索引值所对应的原子的相关系数分成若干组，选取能量最大的一组相关系数对应的原子的索引值存入J0中，完成正则化过程；然后将该索引集J0并入当前支撑集索引Λ中，更新支撑集T并利用最小二乘法进行信号估计，再根据回溯思想，选取前m(m

值得注意的是，现有的重构算法中涉及到正则化优选原子的文献都是根据式0.5|u(i)|≤|u(j)|,i,j∈J进行原子筛选，而本文所提算法采用黄金比例分割法确定正则化过程，根据式0.618|u(i)|≤|u(j)|,i,j∈J进行正则化识别候选集中能量最大的部分原子。黄金比例分割法是一种经典的优化算法，能够以尽可能少的试验次数尽快找到实验中的最优方案，故本文采用此种方法来确定正则化过程能更加精确快速的优选出真实原子，提高支撑集的可靠性。此外，本文所提算法在回溯反馈时，只选取前m(m

输入：测量向量y，感知矩阵Θ，稀疏度K；

1)初始化：迭代次数t=1；残差ro=y；索引值集合J=Ø，Λ=Ø；支撑集T=Ø；

2)计算相关系数u=abs[ΘTrt-1](即计算〈rt-1，θj〉，1≤j≤N)，并将u中绝对值最大的K个值所对应的索引值存入J；

3)正则化：根据式0.618|u(i)|≤|u(j)|，i，j∈J，将J中索引值所对应的原子的相关系数分成若干组，找出能量最大的子集J0；

4)更新Λt=Λt-1∪J0，Tt=Tt-1∪θj(j∈J0)；

6)更新残差

7)t=t+1，如果t≤K则返回第(2)步继续迭代；如果t>K或‖rt-rt-1‖2≤ε则停止迭代；

2.2 基于MRSP算法的CS-ISAR成像

基于本文所提MRSP算法的CS-ISAR成像算法步骤可以描述如下：

1)对雷达回波信号进行脉冲压缩得到频域上的稀疏信号；

2)设计测量矩阵Θ。为了能精确重建出原始信号，测量矩阵Θ与稀疏基Ψ需要满足不相关的要求，故测量矩阵Θ采用随机高斯矩阵，矩阵满足均值为0，方差为1的正态分布。

3)稀疏采样。测量矩阵在方位向总的N个脉冲中随机抽取M个脉冲，即N维的回波信号经测量矩阵Θ降维处理得到M维的观测信号y，这个低维的观测信号包含了重构信号的绝大部分信息。

4)信号重构。采用重构算法MRSP对观测信号y进行重构。选定阈值ε，当残差‖rt-rt-1‖2≤ε时停止迭代，否则继续迭代过程。

5)雷达图像后处理。将重构信号进行适当组合即可得到雷达图像。

3 仿真及实测数据实验

3.1 MRSP算法重构性能验证

为验证该算法的有效性与可行性，分别选取两种信号对该算法进行仿真验证。定义压缩率γ=M/B，M为观测数，N为原始信号长度。

1)随机信号压缩重构

随机产生一个长度N=256，稀疏度K=12的随机信号。采用高斯随机矩阵作为测量矩阵，利用MRSP算法对该随机信号进行重构。实验中选择压缩率γ=0.25，即测量点数M=64。重构信号与原信号的对比如图1所示，重构误差如图2所示。

2)线性调频信号压缩重构

选择线性调频信号s(t)=exp(1.5×1012jπt2)，信号长度取N=1 024。采用离散傅里叶变换构成的正交基作为稀疏基，采用高斯随机矩阵作为测量矩阵，利用MRSP算法对调频信号进行重构。实验中选择压缩率γ=0.5，即测量点数M=512，重构信号与原信号的对比以及重构误差如图3所示。

从以上仿真可以看出使用MRSP算法重建的信号能够较好地反映原始信号，重构误差较小，故MRSP算法重构性能较好，是一种有效可行的重构算法。

3.2 重建性能比较

本部分利用仿真实验验证OMP、SP、MRSP三种算法的信号重建性能。仿真实验选取一个长度为256的稀疏信号，稀疏度为 12，即包含 12个非零随机数，其他元素全部为0。测量矩阵采用高斯随机矩阵。仿真过程中，当残差小于1×10-6时，表示信号重建成功，停止迭代。

为验证测量数M变化对三种算法重建性能的影响，设定量测数从24以等间隔5增加到 256，每个测量数下进行500次蒙特卡洛实验，三种算法重建成功概率结果如图4所示。

可见，当测量数较少时，三种算法的重建概率都较低；随着测量数的增加，三种算法重建概率都逐渐增大。对比来讲，随着测量数的增多，MRSP算法重建成功概率要高于OMP、SP算法。

接下来验证信号稀疏度K变化对三种算法重建性能的影响。设定稀疏度从1以等间隔5增加到70，每个稀疏度下进行500次蒙特卡洛实验，重建成功概率结果如图5所示。

由图5可得，当稀疏度K>16时，OMP算法重建概率开始下降；当K>36时，SP、MRSP算法的重建概率开始下降，但SP算法重建概率下降速度较快，而MRSP算法下降速度较平缓。由此可知，随着信号稀疏度的增加，MRSP算法性能更加稳定、准确重建效果较OMP算法、SP算法更好。

3.3 实测数据成像

本节选取YaK-42飞机的一组实测数据验证本文所提算法成像性能。其相关的雷达参数为：载频5.52 GHz，脉宽25.6 μs，脉冲重复频率400 Hz。实验中选取256个脉冲序列作为全孔径数据量。

为验证本文所提算法的成像性能，对回波信号分别进行传统R-D成像、OMP算法、SP算法以及本文所提MRSP算法成像。仿真时，传统R-D算法利用256个全回波数据进行成像；基于压缩感知的OMP算法、SP算法以及本文所提算法成像时，采用离散傅里叶变换构成的正交基作为稀疏基，采用高斯随机矩阵作为测量矩阵，选择压缩率γ=2/3，即测量回波脉冲个数为M=170。仿真结果如图6所示。

图6(a)是利用256个回波的R-D成像结果，图6(b)—(d)是基于CS算法的成像结果。比较可见，利用CS成像算法，仅需170个回波脉冲即可得到相应的成像效果，甚至更少的回波都能得到有效成像，说明压缩感知方法是有效可行的，能够利用较少的回波数据进行有效成像，在数据完整性、传输以及存储空间等方面具有很高的优越性。

比较图6(b)—(d)成像结果，相同运行环境，相同回波脉冲个数条件下，MRSP算法较OMP算法、SP算法得到的成像结果聚焦性更好、更加清晰。对比这三种成像算法的峰值信噪比PSNR和运行时间：OMP算法的PSNR为5.474 3 dB，运行时间为12.246 1 s；SP算法的PSNR为4.407 8 dB，运行时间为10.420 9 s；MRSP算法的PSNR为5.662 9 dB，运行时间为7.238 4 s；与SP算法相比，MRSP算法成像结果峰值信噪比PSNR提高了约1.2 dB，运行时间提高约30%；与OMP算法相比，MRSP算法成像结果峰值信噪比PSNR提高了约0.2 dB，运行时间提高约40%。由此可以得出，本文提出的MRSP算法与OMP、SP算法相比，成像效果更好、运行时间更短，具有更好的优越性。

4 结论

本文提出了基于改进的正则化子空间追踪算法的ISAR成像方法。该方法采用压缩感知理论，将SP算法与正则化思想结合，采用回溯反馈和贪婪精选的方法进行支撑集选择，并利用黄金比例分割法确定正则化过程实现支撑集的二次筛选，提高了对稀疏信号支撑集的估计精度；减少了传统ISAR成像中对大数据的要求，降低了雷达成像系统的复杂性，以较少的观测信息获得较高质量的目标图像，在一定程度上解决了大量数据传输及存储的难题。仿真实验结果表明该算法对较少的回波数据进行重构，既能获得更加清晰的成像结果，又能进一步提高运算速度，是一种有效可行的重构算法。

参考文献:

[1]江东, 童宁宁, 冯为可, 等. 基于欠定系统局灶解法的逆合成孔径雷达成像[J]. 探测与控制学报, 2016, 38(1)：99-103.

[2]吴敏, 邢孟道, 张磊. 基于压缩感知的二维联合超分辨ISAR成像算法[J]. 电子与信息学报, 2014, 36(1)：187-193.

[3]李文静, 陈红卫. 一种基于压缩感知的ISAR成像方法[J].计算机仿真, 2015, 32(8)：10-13.

[4]Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4)：1289-1306.

[5]黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京： 电子工业出版社, 2005.

[6]李民. 基于压缩感知的雷达高分辨成像技术研究[D]. 哈尔滨：哈尔滨工业大学, 2014.

[7]HuChenxi, Liu Yimin, Li Gang, et al. Improved FOCUSS method for reconstruction of cluster structured sparse signals in radar imaging[J]. Science China Information Sciences, 2012, 55(8)：1776-1788.

[8]Qaisar S, Bilal R M, Iqbal W, et al. Compressive sensing： From theory to applications, a survey[J]. Journal of Communications & Networks, 2013,15：443-456.

[9]Chandran K S, Mishra A, Shirhatti V, et al. Comparison of matching pursuit algorithm with other signal processing techniques for computation of the time-frequency power spectrum of brain signals[J]. Journal of Neuroscience the Official Journal of the Society for Neuroscience, 2016, 36(12)：3399.

[10]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12)：4655-4666.

[11]Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2)：1094-1121.

[12]Dai W,Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5)：2230-2249.

[13]Needell D,Tropp J A. CoSaMP： Iterative signal recovery from incomplete and inaccurate samples[J]. Applied & Computational Harmonic Analysis, 2008, 26(3)：301-321.

[14]丁函,王毅,袁磊,等.一种新的贪婪回溯子空间追踪算法研究[J/OL]. [2016-10-12]. http：// www. arocmag.com/article/02-2017-10-036.html.

[15]梁丹亚, 李宏伟, 李琦,等. 一种改进的压缩感知重构算法[J]. 计算机仿真, 2014, 31(9)：310-313.

[16]李少东,杨军,马晓岩.基于压缩感知的ISAR高分辨成像算法[J].通信学报, 2013(9)：150-157.

[17]Zhang Lei, Xing Mengdao, Qiu Chengwei, et al. Achieving higher resolution ISAR imaging with limited pulses via compressed sampling[J]. IEEE Geoscience & Remote Sensing Letters, 2009, 6(3)：567-571.

[18]Majumdar A, Krishnan N, Pillai S R B, et al. Extensions to orthogonal matching pursuit for compressed sensing[C]//2011 National Conference on Communications (NCC). Bangalore: India Institute of Science,2011： 1-5.

[19]华罗庚.优选法平话及其补充[M].北京：国防工业出版社, 1972.