基于多普勒量测的UKF多目标跟踪方法

，， ，

(空军工程大学信息与导航学院，陕西 西安 710077)

0 引言

弹道导弹在飞行中段为了突破防守，经常会释放伴飞诱饵，形成密集目标群，导致防御系统估计精度低，甚至系统产生崩溃。如何解决此类群目标跟踪问题一直是多目标跟踪领域研究的热点[1]。

基于随机有限集(Random Finite Set，RFS)的多目标跟踪方法，避免了传统多目标跟踪的数据关联，是近年来解决群目标跟踪方法的常用方法。Mahler早在20世纪90年代就提出了将随机有限集运用于多目标跟踪的方法[2-3]，并于2003年通过贝叶斯滤波器的一阶距近似方法，推导出了一种计算可行的概率假设密度滤波(Probability Hypothesis Density, PHD)滤波器[4]；接着，B.N.Vo等人对PHD滤波器进行了工程实现研究，分别通过粒子滤波[5]和高斯混合[6]的形式，使得基于RFS的多目标跟踪方法得以进一步应用。其中，高斯混合概率假设密度滤波器(Gaussian Mixture Probability Hypothesis Density，GMPHD)具有计算复杂度低，容易工程实现等优点，但同时存在方法对模型依赖严重，需要先验信息，而且采用近似方法易导致估计性能较差等问题。本文针对上述问题，提出了基于多普勒量测的UKF多目标跟踪方法。

1 GMPHD算法

1.1 系统模型

假设目标的状态模型服从式(1)：

xk+1=Fxk+vk

(1)

(2)

假定二维直角坐标系下传感器位置在原点s0=0,0T，观测目标与其的斜矩为rk，方位角为θk，多普勒速度为dk。目标的观测模型为：

zk=hk(xk)+wk

(3)

其中，

(4)

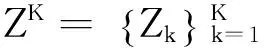
1.2 GMPHD算法流程

高斯混合PHD滤波的基本思想是：在线性高斯系统模型下，将上一时刻的存活目标、新生目标、衍生目标及目标的状态噪声、量测噪声分布分别表示成多个高斯分量的加权和形式，以此来近似目标的PHD；并利用卡尔曼等滤波对高斯分量的均值、方差及其权值迭代更新；在高斯混合分量递推的过程中可以直接提取目标的状态及数目，从而实现对多目标的实时跟踪。

GMPHD算法的流程包括了PHD预测、PHD更新、剪枝与合并、数目与状态估计四个步骤。

1.2.1PHD预测

假设k-1时刻的PHD为高斯混合分布，目标的运动模型为线性或近似线性的，状态噪声和观测噪声均为高斯分布，则k时刻多目标随机集的PHD也服从高斯混合分布。已知在k-1时刻，目标状态的后验PHD为一个高斯混合形式：

(5)

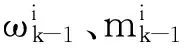
由于衍生部分占总PHD的比例很小，故在此对于衍生部分忽略不计。那么在k时刻，预测目标状态集PHD的高斯混合表示为：

Dk|k-1(x)=Ds,k|k-1(x)+Dγ,k(x)

(6)

其中，Ds,k|k-1(x)、Dγ,k(x)分别表示存活目标和新生目标的PHD。即：

(7)

则，预测PHD为：

(8)

1.2.2PHD更新

已知k时刻目标的预测PHD和量测集Zk，且预测PHD为高斯混合分布，则k时刻目标的后验PHD也是高斯混合分布，可记为：

(9)

1.2.3剪枝与合并

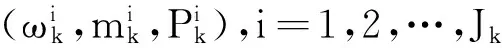
(10)

我们根据上式，进行剪枝与合并，从而降低高斯分量的数目。

1.2.4数目与状态估计

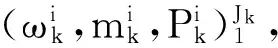
2 基于多普勒量测的UKF多目标跟踪方法

上一章主要构建了GMPHD的算法框架，本章主要给出将多普勒信息融合进框架的算法流程。

在现代战争中，实际采用的雷达，除了目标的斜矩和角度，往往还可以提供更多信息，例如多普勒量测等。理论计算与实践已经证明，充分利用多普勒量测等目标信息不仅可以加强算法的鲁棒性，而且有效地提高对目标的跟踪精度。

在以往的方法中，为了解决带多普勒量测的雷达目标跟踪问题，最常用方法是扩展卡尔曼滤波器(Extended Kalman Filter，EKF)[7]。但存在很明显的问题：此时雷达所提供的量测和目标运动状态之间的关系是完全非线性的，不能满足要求。而且在已有的带多普勒量测的雷达目标跟踪方法中，为了简便方法，文章通常假设斜矩、角度和多普勒的量测误差统计独立，然而最新研究表明[8]，对于某些波形而言，斜矩和多普勒量测误差是统计相关的。

多普勒信息的处理有两个关键步骤：第一，对新生目标PHD的初始化：将多普勒速度和斜矩、方位角量测相结合，计算新生目标强度函数[9]；第二，考虑到量测信息在加入了多普勒速度后高度非线性，同时为了去除目标的多普勒速度和斜矩的相关性，使用UKF对高斯分量进行迭代更新[10]。

2.1 新生目标初始化

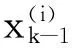
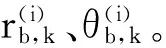
由卡尔曼滤波器公式可得，新生目标初始化速度均值为：

(11)

协方差矩阵为：

(12)

那么在k时刻，式(6)中新生目标状态集强度函数的高斯混合可表示为：

(13)

2.2 高斯分量更新

运用UKF对各高斯混合分量的均值和协方差进行更新，迭代求解。即首先计算采样点及其权值，然后根据状态方程得到点的一步预测，再根据量测方程计算预测的量测，最后结合传感器所提供的量测进行状态更新和状态协方差更新。

(14)

(15)

2)运用量测进行更新分为两步，首先进行一步预测，计算GMPHD预测步骤中的均值与协方差：

(16)

(17)

(18)

进行PHD的预测步骤时，式(8)中的均值和协方差即为式(17)、式(18)的结果。

然后再将预测量测和传感器提供的量测代入，计算GMPHD更新步骤中的均值与协方差：

(19)

(20)

(21)

(22)

(23)

(24)

进行PHD的更新步骤时，式(9)中的均值和协方差即为式(23)、式(24)的结果。

3 仿真实验

本章为验证方法有效性，将本文方法与文献[12]、文献[13]中滤波方法进行比较。性能评价标准采用运行时间、目标个数估计和最优子模式指派(Optimal Subpattern Assignment, OSPA)距离[14]。OSPA距离计算公式为：

式中，p=1，c=300，π∈Πn。

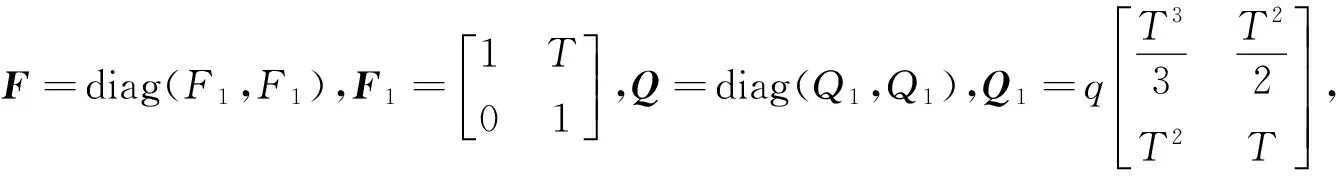
表1 目标初始状态Tab.1 Initial state and tracking of targets

图2是本文方法的单次仿真结果，可以从图上直观地看出，在没有目标初始信息的情况下，由于采用了多普勒信息进行初始化，各个时刻的估计值并未受到杂波的过多干扰，基本上都与真实位置相重合，说明本文方法能够对目标进行有效地跟踪。

为了对本文所提方法有效性进一步验证，将本文方法(UKF-GMPHD)与文献[12](C-PHD)文献[13](GMPHD)中方法进行对比。 真实航迹如图1所示，进行100次独立蒙特卡洛仿真实验平均后，目标的个数估计如图3所示，从图3可以明显看出，在目标出现和消失时，个数估计会产生一定偏差，但本文方法在个数估计基本是无偏的，而GMPHD算法在对于目标个数估计上误差较明显，C-PHD算法由于在滤波过程中同时了进行势分布的运算，所以对于个数估计性能较优，但部分阶段的偏差也大于本文方法，说明本文方法在个数估计上误差较小。

图4为三种方法对于目标估计的OSPA距离，OSPA距离越大，说明方法跟踪性能越差。从图中的曲线可以看出，在目标个数发生变化时，OSPA距离会迅速变大，但是整体看来，本文方法的OSPA距离曲线一直在其他两种方法曲线的下方，说明本文方法在跟踪性能上优于其他两种方法。

图5为三种方法的运行时间比较图，可以清楚地看到，由于其他两种方法采用的是EKF加串行更新的滤波方法，方法复杂度大大提升，所用时间较长，尤其是C-PHD算法，如上文所提，为了保证个数估计的准确性，加入了势估计，使得方法的空间复杂度较大；而本文方法采用UKF滤波方法，不仅减小了目标个数估计的误差，还进一步降低了方法的复杂度，使得方法效率较高，运行时间远小于其他两种方法。

4 结论

基于多目标跟踪的复杂背景，本文在GMPHD的框架下，提出了基于多普勒量测的UKF多目标跟踪方法。该方法通过对多普勒量测的运用，首先实现了新生目标强度函数的去先验自动更新，然后采取UKF对高斯分量进行更新，降低了非线性量测方程的估计偏差。通过仿真实验对比，本文所提方法在目标个数和位置估计精度方面以及方法运算速度方面，均较现有方法有所提高，达到了预期成果。

参考文献:

[1]Tanks R D. NMD： Policy Issues and Technological Capabilities [R]. US: The Institute for Foreign Policy Analysis,2000.

[2]Goodman I, Mahler R, Nguyen H.Mathematics of data fusion[M].Boston： Kluwer Academic Publishers,1997.

[3]Mahler R.Statistical multisource multitarget information fusion[M].Norwood MA, USA： Artech House,2007.

[4]Mahler R.Multitarget Bayes filtering via first-order multitarget moments[J].IEEE Transacions on Aerospace and Electronics Systems,2003,39(3)：1152-1178.

[5]Vo B-N, Singh S, Doucet A. Sequential Monte Carlo implementation of the PHD filter for multi-target tracking[C]// Proceedings of the International Conference on Information Fusion, Cairns, Australia:IEEE,2003：792-799.

[6]Vo B-N, Ma W-K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing,2006,54(11)：4091-4104.

[7]潘泉等.多源信息融合理论及应用[M].北京：清华大学出版社，2013.

[8]韩伟, 汤子跃, 朱振波. 利用ESM方位信息的多普勒盲区目标跟踪方法[J]. 系统工程与电子技术, 2013, 35(8)：1650-1656.

[9] 苍岩, 陈迪, 毕晓君. 自适应GM—PHD滤波器在多目标追踪的应用[J]. 哈尔滨工程大学学报, 2015, 36(11)：1526-1531.

[10]潘泉, 杨峰, 叶亮,等. 一类非线性滤波器——UKF综述[J]. 控制与決策, 2005, 20(5)：481-489.

[11]Mo LB,Song X Q,Zhou Y Y,et al.Unbiased converted measurements for tracking[J].IEEE Trans. on Aerospace and Electronic Systems,1998,34(3)：1023-1027.

[12]Yooh J H, Kim Y, Bae S H, et al. Joint initialization and tracking of multiple moving objects using Doppler information[J]. IEEE Trans. on Signal Processing,2011,59(7)：3447-3452.

[13]胡子军, 张林让, 张鹏. 利用多普勒信息的单步初始化 GMCPHD 滤波器[J]. 系统工程与电子技术, 2014, 36(11)：2122-2126.

[14]刘伟峰，文成林.随机集多目标跟踪性能评价指标比较与分析[J].光电工程，2010，37(9)：14-10.