基于字典学习的图像稀疏去噪算法
,
(1.国防科技大学电子对抗学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
0 引言
图像在获取和传输的过程中常常会受到各种噪声的污染,从而降低了图像的主观和客观质量。噪声的产生使得图像的质量变差,使得人们无法清晰地观测所采集到的图像,影响了视觉效果。图像当中许多重要的细节信息被噪声掩盖,一些需要进行提取和识别的目标也变得无法分析,给后继的图像处理和应用(如图像分割、目标识别、图像检索以及图像编码、传输等)带来了诸多不利的影响。因此,图像去噪问题在图像预处理中起着至关重要的作用。
近年来,一些基于自然图像稀疏性表示的去噪方法被提出来[1-4]。信号稀疏表示理论将信号由非稀疏域转变为稀疏域,通过捕获信号的有用信息来进行信号的处理,更好地重构出原有信息。利用图像中的有用信息一般具有稀疏性,而噪声不具有稀疏性这一特点,从而将图像中的噪声去除[5]。图像的稀疏性可通过稀疏变换实现,那么选择一个合适的稀疏变换基是图像重构精度的关键问题。
当前应用广泛的一类稀疏字典为冗余字典,根据构造方法分为两类:根据固定参数构造字典和基于样本训练方法构造字典。参数化构造的冗余字典有:Gabor字典[6]、DCT[7]字典等。文献[8]为实现图像的稀疏表示,文中构造了由多个方向字典和一个正交DCT 字典组成的冗余字典,并用l1范数作为约束条件求解稀疏优化问题。由于图像是复杂的二维信号,参数化方法构造的字典不能充分体现图像的几何特征,虽然构造简单,但是不能有效表示图像的具体结构特征,不能自适应复杂的图像结构,稀疏效果并不理想。
本文针对此问题,提出了基于字典学习的稀疏去噪算法。基于样本训练方法构造的字典具有自适应性,能够使稀疏变换系数有较高的稀疏度。
1 基本理论
1.1 稀疏表示
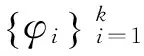
(1)
其中,αi=〈x,φi〉是x在基函数φi上组成的矩阵。由于基是线性独立的,因此展开式是唯一的。式(1)可以表示为:
x=Φα
(2)
其中,Φ∈Rn×K是基函数组成的矩阵,矩阵的每一列对应一个基。α∈Rk则是展开的系数所组成的矩阵。
通过K-n与零的关系,则可以将函数集合分为非完备、完备以及过完备这三类。当小于零时,那么空间中的某些向量不能够被φi完整的表示,此时我们则认为φi为非完备的;当公式等于零时,那么这K个基向量φi组成了一组过完备基;当公式大于零时,空间中的每一个向量都可以用φi的线性组合表示,并且表达式不唯一,对应的α有无穷多个解,此时我们称基函数的组合φi为过完备的。
1.2 冗余的稀疏表示
随着研究的不断深入,冗余字典代替传统的标准正交基成为一种趋势[10]。这是因为冗余字典可以通过训练样本得到,这就使得冗余字典中的原子与逼近信号有一致的结构,从而进行稀疏表示的时候使用的原子的数目较少,即使得信号更加稀疏,因此可以更好的还原信号。
为了更加灵活、精简地表示信号,Mallat在小波分析的理论基础上,研究了传统的正交基在稀疏表示中的缺点,设计了冗余的字典,并且从中找到了一组最佳的线性组合来表示信号,此时线性组合的系数几乎为0,即为稀疏的[11]。设存在信号x∈Rn和冗余原子库D∈Rn×K;原子库由K个原子组成,且K>n。则有
x=Dα
(3)
其中,D∈Rn×K,它的每一列代表一个原子。在已知D的情况下,x的冗余表示为α。从前面的分析可得,α存在无穷多个解,是一个欠定问题。对于该问题的求解,常见的方法包括正交匹配追踪(OMP)算法[12]、基追踪降噪(BPDN)算法[13]以及SLO算法[14]等。
2 基于字典学习的稀疏去噪
算法流程如图所示。首先是对噪声图像进行分块处理,然后通过基于噪声图像块进行训练字典,初始化字典选择是冗余的离散余弦变换字典(研究表明了当初始化字典选择冗余的DCT字典时,使用稀疏分解的算法迭代次数将会明显降低,可以得到比较理想的效果),采用K-SVD算法对字典训练。再用训练得到的字典对每个块进行稀疏分解,对得到稀疏分解进行局部到整体的平均处理,最后得到去噪图像。
2.1 离散余弦字典
离散余弦字典(DCT)是由离散余弦变换所得,给定序列x(n),n=0,1,…,N-1,其离散余弦变换:
(4)
(5)
矩阵形式:
Xc=CNx
(6)
其中,CN是N×N变换矩阵,其行向量为余弦基。
对于DCT变换后所获得的完备字典,采用分数频率法将其扩展成为过完备字典,具体的做法是将得到的完备字典对其频率上做更加精细的遍历和抽样,从而获得一个新的过完备字典。
2.2 基于K-SVD的字典训练
2.2.1K-SVD算法
噪声图像x中每一个图像块信息xij,可由训练得到的字典D中少数几个原子(列) 的一个线性相关表示:x=Dα,其中,α∈Rn×N是x的稀疏表示系数,且要求满足一定的稀疏度:
(7)
其中,ε为误差上限,上式可优化为:
(8)
K-SVD的目标函数为:
(9)
其中Rij为索引矩阵,Y为去噪目标图像。通过下式估计第i列的误差值:
(10)
K-SVD算法的主要任务是在迭代过程中交替更新字典D和稀疏系数α,最终可以得到以下去噪模型:
(11)
其中,I为单位矩阵。
2.2.2字典学习
文献[15]提出了基于K-SVD训练算法来得到过完备字典的思想,通过进行K-SVD算法对初始图像训练,由于训练得到的字典包含图像的先验信息因此能够反映图像的结构特征,所以在去噪的同时可以保留图像原有的细节信息。
基于K-SVD的字典学习有两种构建原子库的方式,一是选取和待处理图像相似的图像样本作为字典学习的图像训练集,另一种方式是用待处理本身的图像进行字典训练。前者得到的是一个全局字典,而后者由于在训练过程中可以根据不同图像的不同特点来调整,因此得到的字典称为自适应字典。
2.3 OMP算法
OMP算法主要思想为按照匹配度选择最优的原子进入原子集,求出测量信号在原子集的正交空间上的投影,通过求解一个最小二乘问题来求得原信号的最优稀疏逼近解,更新信号余量,进入下一次迭代,经过一定迭代过程,最后用原子对信号进行线性表示。具体实现步骤如下:
输入:M×N维测量矩阵,采样信号Y,稀疏度K;
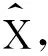
步骤1 索引集Λ0=∅,迭代次数t=1;
步骤2 找到索引集Jt,使得Jt=
argmaxi=1,2,…,n
步骤3 令Λt=Λt-1∪{Jt};
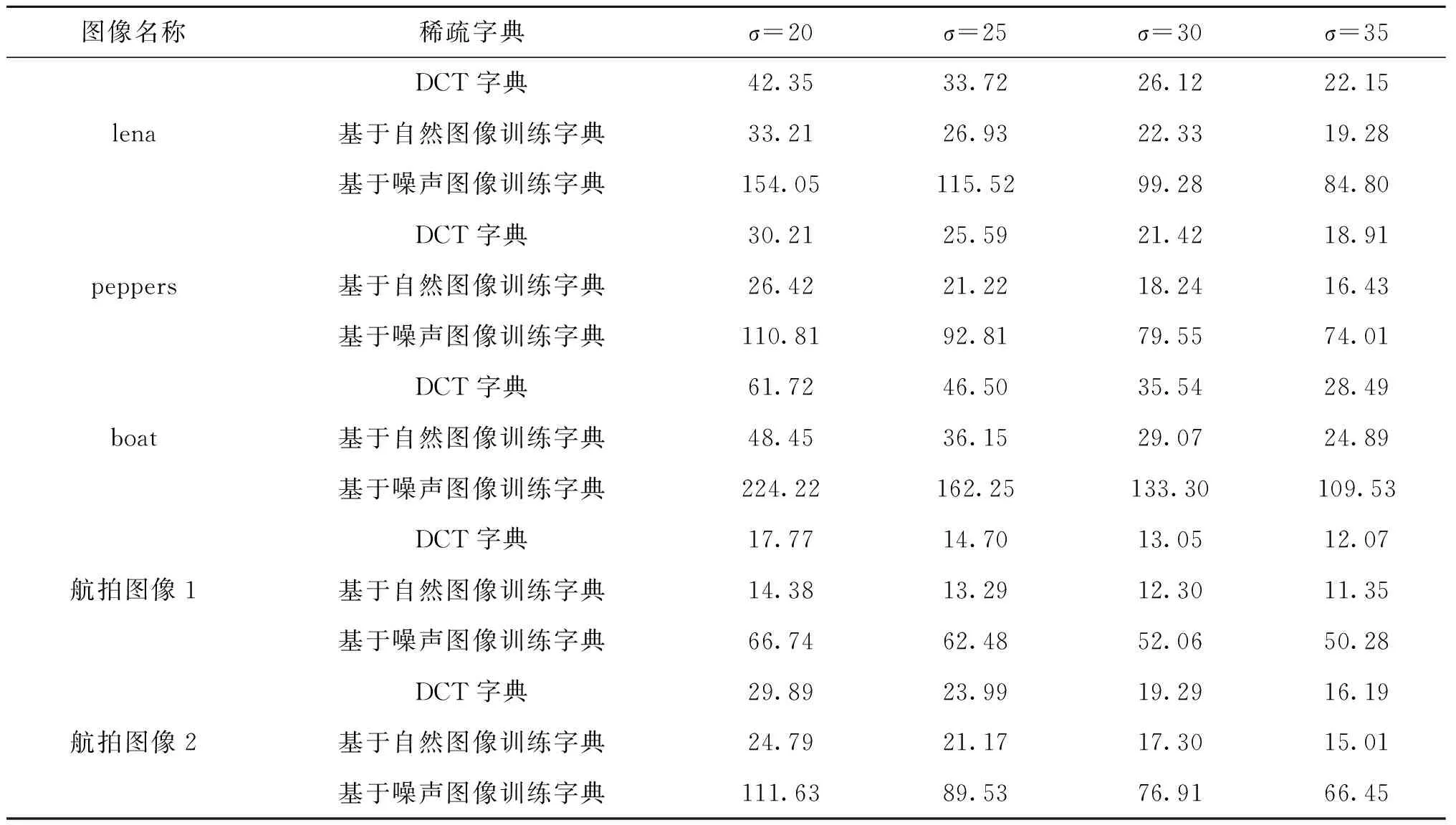
步骤6t=t+1,如果t 步骤1 将图像x按8×8大小进行分块处理。 步骤2 对图像块进行稀疏变换,对噪声图像块进行训练字典。 步骤3 字典初始化:设置DCT字典D∈Rn×L。 步骤5 更新字典:当稀疏表示完成后,忽略惩罚项‖αj‖0, 步骤6 对Ek进行奇异值分解得到Ek=UΔVT。U的第一列为主向量,将dk更新为U的第一列,同时αk更新为V的第一列与对角阵Δ的第一个值Δ(1,1)的乘积。 步骤7 将奇异值分解应用到残差矩阵的分解中,逐列更新字典中的原子;同时更新稀疏系数。回到步骤4,直至达到退出条件。 步骤8 得到去噪后图像Y。 为了比较基于稀疏表示的图像去噪算法利用K-SVD算法训练字典时,几种不同稀疏字典对实测图像重构质量的影响,利用Matlab进行实验仿真。测试图像为3幅自然图像lena图像、peppers图像和boat图像,以及2幅实测图像包括航拍图像1和航拍图像2,如图3所示,5幅图像大小均为512×512。对比的稀疏字典为DCT字典、K-SVD算法对自然图像样本训练所得字典以及K-SVD算法对噪声图像训练所得字典。实验所用软件为Matlab R2014a,选用2.6 GHz,2G内存的计算机平台。 为了对本文各组实验图像质量进行定量分析,利用峰值信噪比(PSNR)对去噪图像效果进行比较。其中,PSNR计算表达式如式(12)所示。 (12) 式中,I0(i,j)为原图像,I1(i,j)为去噪后图像。 首先,设置图像的分块大小B=8。其次测量矩阵采用正交高斯随机矩阵,重构算法选取正交匹配追踪算法(OMP)。采用三种不同字典的稀疏方法对5幅图像分别添加σ=20,25,30,35随机噪声,以保证实验可靠性。 为观察基于K-SVD算法对噪声图像训练得到的稀疏字典,对5幅图像添加σ=35随机噪声,结果如图4。 同时,以航拍图像1为代表,在σ=20,25,30,35随机噪声下,航拍图像1的基于噪声图像训练字典如图5所示。而对5幅图像添加不同随机噪声,在图像去噪过程中,得到另外两种稀疏表示方法的字典是固定字典,实验结果如图6所示。 图7给出了航拍图像1分别在σ=20,25,30,35随机噪声下,字典学习过程中每次迭代后的稀疏系数值,在达到设定条件迭代次数为10后退出循环。从图中可以看出,噪声越大每次迭代的稀疏系数越接近零。 通过图4、图5、图6的对比,可以看出三种字典有很大不同,说明KSVD算法在迭代过程中通过稀疏系数不断调整冗余字典中的原子,大幅度改进了原字典的结构,最终获得能更加有效反映图像各结构特性的冗余字典。图4和图5验证了不同类型图像不同程度噪声时,对噪声图像用K-SVD算法训练得到的字典是不同的,这种稀疏表示方法具有自适应性,图像去噪性能更优。 图6(a)是DCT冗余字典,实验中使用的初始化字典;图6(b)是对DCT冗余字典在图像样本集下用K-SVD算法训练后,获得的基于自然图像训练字典。尽管该字典是训练得到,但在不同情况下,这些自然图像样本依然不变,最终得到的是同一字典,和基于噪声图像训练的字典相比,不具有自适应性。 为了保证实验的可靠性,对不同类型图像添加相同噪声,分别对5幅图像添加35%的随机噪声,实验仿真了三种字典的稀疏方法去噪结果,如图9所示。并绘制了5幅图像在σ=20,25,30,35随机噪声下去噪后峰值信噪比(PSNR)的折线图,如图10所示。 从图8和图9可以看出,不同类型图像受不同程度噪声干扰后,基于学习字典的图像稀疏去噪方法去噪性能均优于基于固定字典的图像稀疏去噪方法,其中基于噪声图像训练字典的方法随着噪声增加去噪效果比基于自然图像训练字典的方法好。同时当图像细节较多时,lena图像、boat图像在受随机噪声干扰较小时,基于自然图像训练字典的方法与基于噪声图像训练字典的方法相比,去噪效果稍好。这是由于在低噪声下,图像具有丰富的细节信息,此时对多幅自然图像训练所得字典对图像稀疏表示更加稀疏,能更好地重构图像。 在稀疏编码过程中,使用OMP算法对训练集中每个信号的稀疏表示,测量矩阵采用高斯随机矩阵,表1给出了在算法迭代中一个信号的稀疏表示。该信号的稀疏系数矩阵大小为256×65 000,可以看出,此时稀疏系数矩阵几乎为0,是稀疏的。 表1 信号的稀疏表示Tab.1 Sparse representation of the signal 图10给出了此时更新稀疏系数时的残差(余量),其矩阵大小为64×1,为了方便显示,将其排列成8×8矩阵形式。同时计算得到索引集为{4,8}。 图9以PSNR为评价标准,将3种算法对图像去噪质量的影响进行了分析比较,但算法复杂度也是评价算法优劣的一个重要指标,本文通过实验仿真计算了3种算法重构所需时间,如表2所示。 图像名称稀疏字典σ=20σ=25σ=30σ=35lenaDCT字典42.3533.7226.1222.15基于自然图像训练字典33.2126.9322.3319.28基于噪声图像训练字典154.05115.5299.2884.80peppersDCT字典30.2125.5921.4218.91基于自然图像训练字典26.4221.2218.2416.43基于噪声图像训练字典110.8192.8179.5574.01boatDCT字典61.7246.5035.5428.49基于自然图像训练字典48.4536.1529.0724.89基于噪声图像训练字典224.22162.25133.30109.53航拍图像1DCT字典17.7714.7013.0512.07基于自然图像训练字典14.3813.2912.3011.35基于噪声图像训练字典66.7462.4852.0650.28航拍图像2DCT字典29.8923.9919.2916.19基于自然图像训练字典24.7921.1717.3015.01基于噪声图像训练字典111.6389.5376.9166.45 由表2结果可知,基于噪声图像训练字典的稀疏表示方法进行图像去噪时,其复杂度最高,该方法的稀疏字典在训练过程中K-SVD算法需要进行迭代来达到字典要求,运行时间会明显高于其他两种方法。基于DCT字典和自然图像训练字典的稀疏表示算法去噪程序运行时间明显少于基于噪声图像训练字典的稀疏表示算法。对于图像细节信息较多的lena和boat,三种算法程序运行时间比其他图像相比均较高。 本文提出了基于字典学习的图像稀疏去噪算法。该算法对图像进行分块处理,通过基于噪声图像块训练字典,采用K-SVD算法对初始化DCT字典训练,然后用训练得到的字典对图像块进行稀疏分解。仿真实验结果得出,不同稀疏字典的稀疏去噪方法对具有不同细节信息的图像去噪性能影响,在不考虑算法复杂度前提下,基于噪声图像训练字典的图像稀疏去噪算法与其他两种算法相比去噪性能较好。 参考文献: [1]Aharon M, Elad M, Bruckstein A. The K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11):4311-4322. [2]张敏. 基于KSVD的双字典学习算法及其在图像处理中的应用[D].北京:北京工业大学, 2015. [3]何俊飞, 李峰, 张建明,等. 使用双稀疏的图像去噪算法[J]. 小型微型计算机系统, 2015, 36(5):1109-1112. [4]高美凤, 王晨. 基于联合滤波的聚类稀疏表示图像去噪算法[J]. 计算机工程与应用, 2015, 51(24):180-185. [5]宋成伶. 基于稀疏表示的图像去噪的研究与实现[D].南京:南京邮电大学, 2016. [6]詹曙, 王俊, 杨福猛,等. 基于Gabor特征和字典学习的高斯混合稀疏表示图像识别[J]. 电子学报, 2015, 43(3):523-528. [7]钟桦, 焦李成, 潘秋丰,等. 基于DCT字典同步稀疏表示的SAR图像降斑方法: 中国,CN103077503A[P]. 2013. [8]练秋生, 周婷. 结合字典稀疏表示和非局部相似性的自适应压缩成像算法[J]. 电子学报, 2012, 40(7):1416-1422. [9]邓承志. 图像稀疏表示理论及其应用研究[D].武汉:华中科技大学, 2008. [10]高广春, 尚丽娜, 熊凯,等. 冗余字典在压缩感知中的应用研究[J]. 电路与系统学报, 2012(6):107-110. [11]刘世凯. 基于稀疏表示的边缘保持图像去噪方法研究[D].北京:北京理工大学, 2015. [12]Tropp J, Gilbert A. Signal recovery from random measurement via Orthogonal matching pursuit[J]. IEEE Trans. Inf. Theroy, 2007, 53(12): 4655-4666. [13]Cai T T, Xu G, Zhang J. On recovery of sparse signals via1minimization[J]. IEEE Transactions on Information Theory, 2009, 55(7):3388-3397. [14]Mohimani H, Babaie-Zadeh M, Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed0norm[J]. IEEE Transactions on Signal Processing, 2008, 57(1):289-301. [15]Ranjan Maitra, Thomas Mathew. Analysis of variance in statistical image processing[J]. Technometrics, 2000, 42(2):212-213.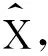
2.4 算法步骤
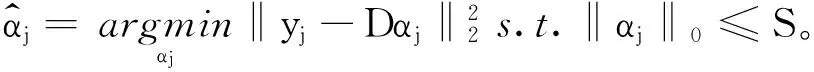
3 实验仿真与分析

4 结论

