最小偏差法船舶调度

林 辉， 陈顺怀

(武汉理工大学 a.交通学院, b.高性能船舶技术教育部重点实验室， 湖北 武汉 430063)

0 引 言

在世界海洋运输业迅速发展的今天，船舶调度作为港口调度的关键内容之一，从20世纪50年代开始就引起了许多学者的关注。船舶调度是一种能降低船务公司营运成本的手段。船舶调度方案的优劣直接关系到船舶航运过程中的船舶运输效率、油耗情况以及港口成本等诸多经济效益的好坏，从而对航运公司的盈利能力产生实质性的影响，因此对配船方案的优化就显得尤为重要。配船方案的优化过程涉及诸多问题，比如船舶运输成本的构成、客流量的满足、船舶速度和航行时间的匹配等。因此，船舶调度优化是一个多目标优化问题。

每条航线的配船方案和调度是由船务公司的专门调度人员负责安排的。一般来说，在船舶调度中所考虑的问题有许多是随机可变的，比如本文所讨论的客船调度，除淡季和旺季的客流量差异以外，其每日的客流量也是随机变化的，还有水域、天气条件也会有所差异。这些都成为影响船舶调度方案优劣的约束条件。

现今，绝大多数船舶(包括集装箱船、散货船、客船)的配船主要还是依靠专门调度人员的经验，以至于现有的船舶运输资源未得到充分的利用，从而导致运输成本相对较高，并且不能较好地满足客户的需求。因此，采用合适的方法对该问题进行优化处理非常重要。目前，已有许多学者采用蚁群算法等相关算法进行求解优化，本文在其后也对其进行了一些比较。

1 遗传算法及最小偏差法简介

1.1 遗传算法及其基本理论

遗传算法(Genetic Algorithm，GA)是一种自适应全局优化搜索算法。它主要借鉴生物在繁殖生存过程中的遗传和进化规律。早在20世纪60年代, HOLLAND就提出GA算法的理论;20世纪70年代， JONG首次根据GA理论开展计算机数值试验；20世纪80年代， GOLDBERG对之前学者所做的理论和试验研究进行总结归纳得到现今的经典遗传算法。

GA是一种传统的智能算法，它有良好的随机性和全局性，是一种高效的、并行的、全局性的成熟优化方法。经典遗传算法的优化变量是采用二进制码来描述的，多个优化变量的二进制码串接在一起形成一组染色体，这种编码方式既适用于变异操作，又可对其进行交叉操作。在创建初始种群时，代表个体的二进制串是在一定字长的限制下随机产生的。GA算法中的交叉算子其主要功能是交叉2条染色体，交叉位置是随机产生的，染色体的交叉位置也是随机选取的，从而保证后代的随机性，2个染色体在进行随机交叉后，其对应位置的二进制码将进行交换并生成新的2个染色体。变异算子作用在单一染色体上，通过1个随机概率对单个染色体上的二进制码进行变异，即将“0”变异成“1”，或者将“1”变异成“0”，从而得到新的染色体。最后将这些不断交叉变异的个体代入适应度函数进行计算，比较适应度值之间的差异是否满足精度要求，满足精度要求即可获得全局最优解。

1.2 最小偏差法

在实际的多目标寻优过程中，由于约束条件和优化目标较多，往往很难求得最优解，故在工程应用中主要以寻找多目标优化中的满意解为最终优化目标。本文采用的最小偏差法就是一种可用于多目标问题优化的决策方法。

常见的多目标优化模型可以表示为

x∈Rn(1)

式中：f1(x),f2(x),…，fl(x)为l个极小化目标函数；fl+1(x),fl+2(x),…，fm(x) 为m-l个极大化目标函数；gj为线性、非线性不等式函数式；hk为线性、非线性等式函数式；j为不等式约束编号，其值为1，2,3，…；k为等式约束编号，其值为1,2,3，…；x为决策变量，x=(xl,x2,…，xn)T。

多目标优化问题的核心思想是将多个适应度函数同时求取最优解，但是由于不同适应度函数的最优解必然是不同的值，故而在多目标优化问题中引入较优解的概念,即多个适应度函数在较优解的情况下，可同时获得相对较优的适应度值。1951年，TKOOPMANS提出一种与较优解概念相同的有效解概念，被称之为Pareto最优解。Pareto最优解是通过对多个适应度函数构成的向量函数的适应度值进行大小比较获得的。

假设X⊆Rn是多目标优化问题的约束集，若x*∈X，且不存在x∈X使得∀i∈(1,2,…,l),fi(x)≤fi(x*)，而对于∀i∈(l+1,l+2,…,m),fi(x)≥fi(x*)，则称x*为其有效解[4-5]。

对于多目标优化问题，主要工作就是寻找合适的方法来获得目标的Pareto最优解，因此，寻找一种合适的决策函数来处理多个适应度函数，使其能进行相互比较就成了关键性问题。如式(2)所示，可以通过一定的权重策略将m个函数式构成1个以x为自变量的复合函数式：

F′(x)=F′(f1(x),f2(x),…，fm(x))(2)

对式(2)中多个适应度函数共同优化问题的解是一个解集，即不只存在一个解，不同的决策方法和求解算法获得的解不尽相同，其具有的意义也存在差异，本文采用最小偏差法[5-6]作为统一适应度函数的决策方法：

2 船队调度优化模型的构建

本文主要以迅隆公司的船舶调度案例为基础，结合其公司船舶数量、航线情况和航班要求等基础条件建立数学模型。

迅隆公司拥有6艘客船构成的船队，将这6艘客船分别命名为迅隆1～6号。船型的不同导致每条船的载客人数和每公里耗油都有差异，此外所需船员人数也不同。船队航行的航线主要有4条，分别是蛇口-中环、蛇口-澳门、蛇口-机场和福永-澳门。耗油量的不同可能由航线里程和水域状况的不同导致，不同船型的吨位不同导致其在港口的停泊、服务等综合费用也存在较大的差异[8]。

2.1 航运成本组成部分

耗油量：不同船舶的主机在不同单位时间和单位里程的油耗存在较大差异。本文按如下的公式计算主机在船舶往返航班中的油耗成本：

往返航班油耗成本=往返航班里程×

油耗×单位油价 (4)

人员工资：出航的工作人员除了有基本的工资、伙食补贴之外，还有按出勤天数计算的奖金。本文通过相关薪资数据，按如下公式计算船员的航行补贴：

航行补贴=航班数×基本航线补贴×航线系数 (5)

港口费用：由于不同吨位的船舶在不同的港口收费标准存在差异，故必须根据码头的实际情况获取港口费用。

2.2 目标函数

2.2.1 总成本最小化

该优化模型以船舶日总成本费用最小化为目标构建优化模型，其中包括成本、码头综合管理费用和船员津贴成本(船员工资为固定成本，此处不作考虑)。

(1) 船舶油耗成本。不同船型的船舶在不同航线上由于主机油耗和航程的不同，成本也不尽相同，此处令不同船舶在不同航班上的油耗成本为oij，则

oij=xij×cij(6)

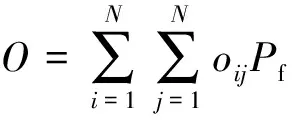
式中：xij为船舶i开往往返航班j的次数，xij∈(0,1)。它是模型的0-1变量，决定了本研究所建立的数学模型将是0-1整数规划。具体含义如下：

(8)

式中：cij为船舶i开往往返航班j的耗油量；Pf为单位油价；i为船舶编号，i=1,2,3,…,M，M为船舶数量;j为往返航班编号，j=1,2,3,…,N，N为航班数量。

(2) 船舶码头管理综合费用。由船舶i在往返航班j中的码头使用费用Wij得到1天中所有航班所需要的码头总费用为

“张勇说得已经非常直白，花如此巨资直接收购而不是战略投资饿了么，说明饿了么对于阿里未来发展之重要性，就是成为新零售战略的重要力量。”何军向《中国储运》杂志记者阐述了自己的观点。

(9)

式中：Po为1天中所有航班所需码头费用；Wij为船舶i在往返班j中的码头使用费。

(3) 船员工资。针对人员薪资基本维持不变的特性将其不予考虑，只在数学模型中包含航线补贴的计算，而略去基本工资总额。船舶i开往往返航班j支付给船员的总补贴为ρj·Cri，因此1天中往返航班总补贴P为

ρj·Cri(10)

式中：ρj为船舶往返航次数j的相关补贴系数；Cri为船舶i所有船员的基本航线补贴。

综上所述，船队1天的成本最小化目标函数为

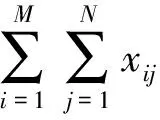
2.2.2 空载率最小化

班轮在营运过程中，在满足当天游客数量的前提下，使船舶空载率最小化，充分利用船舶的运营空间，其中的客流量Fpk使用现有的载客能力估计。于是有

,k∈SK(12)

式中：SJKk为航线k往返航班的集合；si为船舶i的座位数；Fpk为航线k的日平均客流量，人；SK为航线集合。

2.2.3 船舶调度次数差异最小化

为使船舶调度便利，M艘船舶在N个往返航班被调度的期望次数为N/M，故其第3个目标函数为

,i=1,2,…,M(13)

2.3 基于最小偏差法统一目标函数

综合上面的目标函数，得到班轮调度的多目标优化模型为

(14)

根据上述多目标优化模型和最小偏差法[7]，得到统一的目标函数为

式中：C1max，C2max，C3max和C1min，C2min，C3min分别为各目标函数在约束条件作为单目标函数进行寻优求解的最大值和最小值。

2.4 约束条件

该船队调度优化模型共有3组约束条件。

(1) 对于任一航班都须并且只须1艘船。

,i=1,2,3,…,M；j=1,2,3,…,N(16)

(2) 避免船舶在往返过程中的时间冲突。比如往返航班1和7的时间段有交集，不可能使用同一艘船舶。

xij1+xij2≤1

∀i=1,2,…,M,j1,j2=1,2,3,…,N

且j1≠j2,Ωj1∩Ωj2≠Ø(17)

(3) 每艘船舶至少被调动1次，以充分利用船队资源。

≥1,i=1,2,3,…,M(18)

3 算法运行和结果分析

3.1 基于最小偏差法遗传算法寻优步骤

本文借助MATLAB中的GA Toolbox进行求解[9]。由于班轮调度属于0-1整数规划问题，这里采用工具箱中的整数规划遗传算法工具箱进行求解。

(1) 由于最小偏差法中须得到同等约束条件下多目标中各目标函数的最大值和最小值，传统优化算法对初始解的选取较为敏感，为确保寻优结果，先采用MATLAB中遗传算法工具箱进行单目标问题的模型构建和求解，得到其最大值和最小值。

(2) 利用式(1)中计算出的最大、最小值代入最小偏差法构建的多目标优化模型中，通过MATLAB工具箱进行求解。

3.2 优化结果及分析

在完成MATLAB平台上优化模型的目标函数和约束条件的编写后，运行该优化算法，在遗传算法中，可以对其遗传策略进行设置，不同的遗传策略得到的优化方案不同。本文通过改变EliteCount这一遗传参数来得到较优方案，然后将较优方案与原方案进行对比。班轮公司现采用的方案如表1所示。

表1 原调度方案

通过遗传算法进行优化后的结果如表2所示，其过程如图1所示，优化调度方案如表3所示。

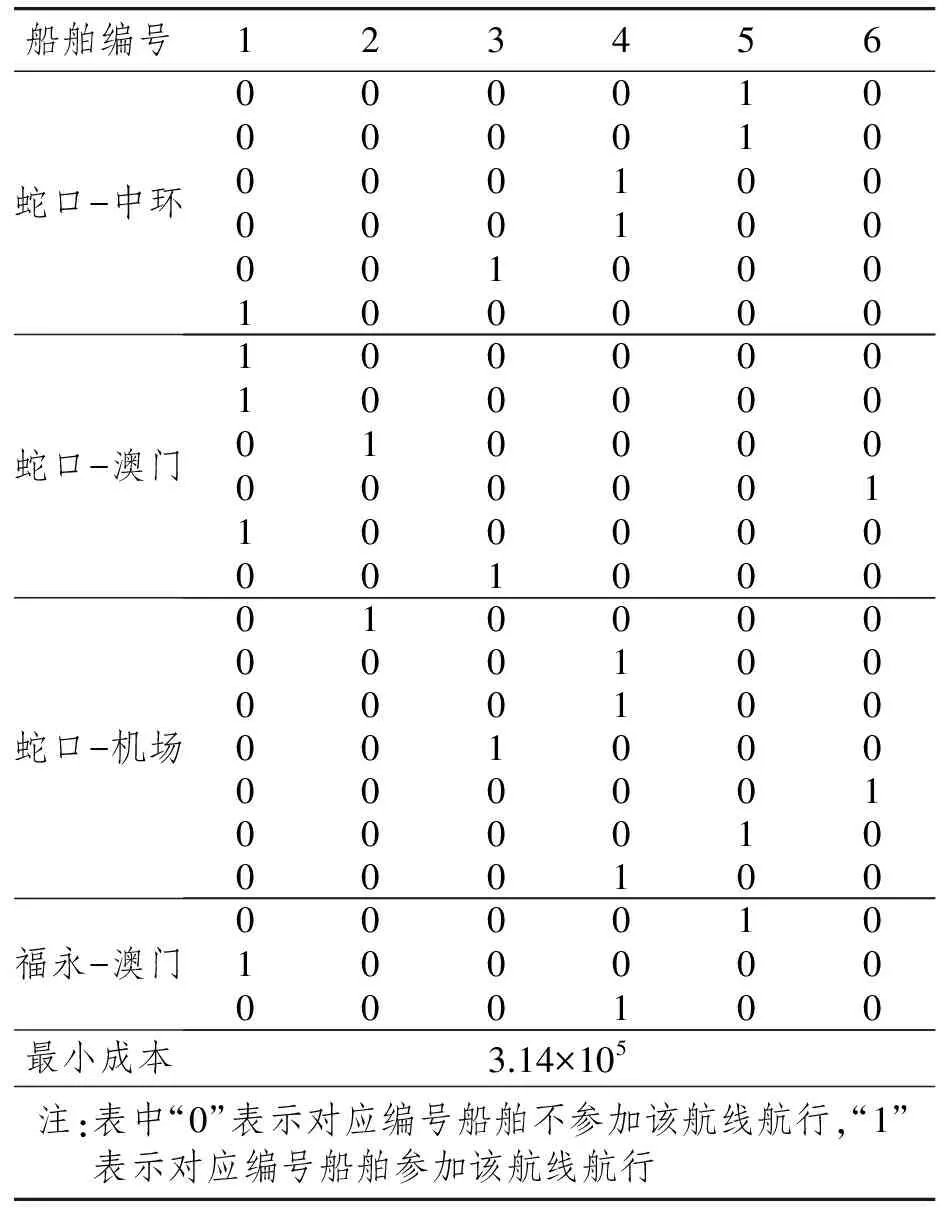
表2 优化结果

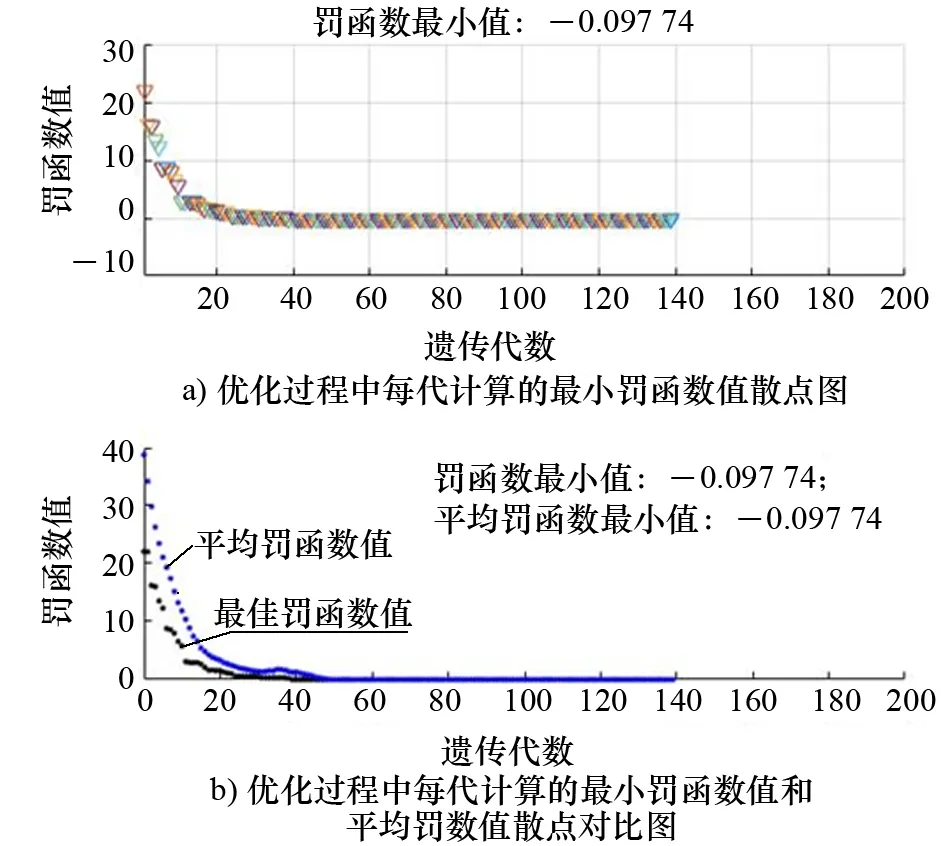
图1 遗传算法优化过程

航线编号航班编号船舶编号航线编号航班编号船舶编号1152123125313213431441443154153316316131762713185281319429242052106421121114224

方案对比结果如表4所示。

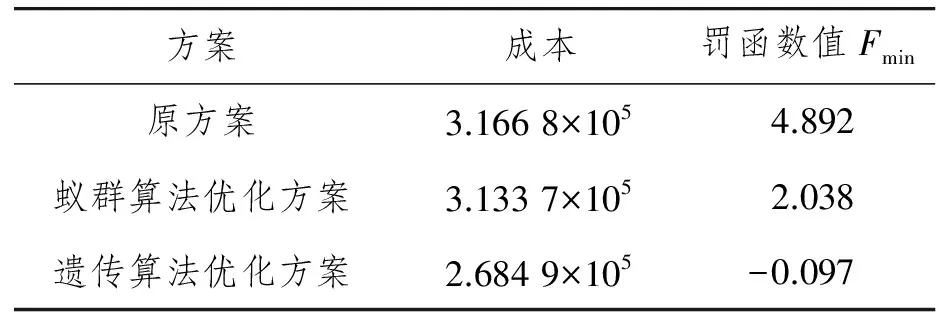
表4 3种方案的对比结果

由表4的数据分析可得：通过遗传算法进行整数规划得到的方案较原方案有明显的优势，除此之外，也比传统蚁群算法优化得到的方案[10]较优。

4 结 论

本文利用实际船舶公司的数据对船舶调度问题进行分析研究，以MATLAB为计算平台，构建遗传算法优化模型，采用最小偏差法处理船舶调度中的多目标优化，得出以下结论：

(1) 文中针对的班轮调度优化结果与原方案进行对比可得：类似船舶调度类的问题可通过采用类似整数规划的方式进行优化，这不仅可以将船舶运输效率最大化，同时营运成本最小化。

(2) 本文采用的遗传算法优化后结果与原方案相比较好，验证了遗传算法在多目标混合整数0-1规划问题中的应用优势性和合理性。

(3) 本文主要以MATLAB进行计算，可见MATLAB在工程计算中应用的便利性、合理性。

(4) 在船舶实际调度过程中还有很多因素参与影响，本文仅从成本、空载率和差异化这3个目标进行优化，故还须在日后的研究中考虑更多因素，完善调度方案，以使方案更贴近实际调度情况。

[ 1 ] 吕如福. 多目标船舶调度优化问题蚁群算法研究[D]. 杭州：浙江大学,2010.

[ 2 ] 王中华. 基于遗传算法的港口船舶调度优化问题研究[D]. 上海：上海海事大学,2007.

[ 3 ] 王冲, 茅云生, 辛锺桂. 基于遗传算法的船舶分段运输调度方法[J]. 上海交通大学学报, 2017, 51(3):338-343.

[ 4 ] 钱燕, 周良. 基于遗传算法的不定期船舶调度优化模型研究[J]. 计算机与数字工程, 2014, 42(4):601-605.

[ 5 ] 周美英, 李典庆. 多目标优化设计的最小偏差法[J]. 机械设计, 2002, 19(12):50-52.

[ 6 ] LI W L, TAN J H. Optimization of Container Ship Principal Parameters based on Minimum-Deviation Method[J]. Shipbuilding of China, 2002, 43(4):1-5.

[ 7 ] WEI F T, SONG L, YAN L. Application of Minimum-Deviation Method to Mechanical Multi-Objective Optimal Design[J].Journal of Engineering Graphics, 2011, 32(3):100-104.

[ 8 ] 王文全, 黄胜, 侯远航,等. 基于改进人工蜂群算法的大型舰船主尺度优化[J]. 武汉理工大学学报, 2012, 34(6):58-62.

[ 9 ] 周俊杰.Matlab/Simulink实例讲解[M]. 北京：中国水利水电出版社,2014.

[10] 张新宇, 林俊, 郭子坚,等. 基于模拟退火多种群遗传算法的港口船舶调度优化[J]. 中国航海, 2016, 39(1):26-30.