曲率差型模态在压电陶瓷探伤中的分析

祝敏

(昆山佰奥智能装备股份有限公司，江苏 昆山 215300)

0 引言

压电陶瓷片结构简单造价低廉，用途广泛。由于压电陶瓷器件通常是在循环交变电场下服役，或在多场合下工作，极易产生裂纹等各类缺陷，影响结构的安全运行，甚至使结构整体失效，造成重大的安全事故和人员伤亡[1]。因此器件的可靠性和失效问题一直是人们关注的焦点，而其中内部裂纹和电击穿等失效问题已成为压电陶瓷器件广泛应用的主要障碍，也是其可靠性和耐久性设计考虑的重点。为保证结构的安全与系统的正常工作,需要定期或在线对压电陶瓷进行损伤检测，尽早地发现损伤发生的位置和程度,对结构实时进行修复或改进,避免灾难性事故的发生。

压电陶瓷片由于其所具有的双向机-电耦合特性,还在混凝土的无损监测中具有其独特的优势。 姜德义[2]等人运用有限元分析软件对埋置于混凝土中的压电陶瓷片的耦合振动模态进行了分析研究，结果表明ANSYS能很好地解决压电陶瓷片的自由度耦合问题及压电耦合问题，为压电机敏混凝土健康安全监测技术的进一步研究提供了一种有效支持。王锋等人[3-4]以应变模态振型和应变模态差为损伤识别指标对悬臂梁损伤进行了有效的识别。发现应变模态振型对非模态节点损伤非常敏感，得出了损伤附近应变模态发生突变,并且突变程度随损伤量的增加而增大的结论。

然而，关于如何识别压电陶瓷片上是否存在微裂纹等缺陷的研究非常少，本文第一次将曲率差型模态这种探伤方法应用到压电陶瓷片上，并从理论上证明了该方法的可行性。

1 损伤模拟理论

结构最基本的模态信息是固有频率,测量容易且精度高。根据结构动力学理论,一旦结构发生损伤,结构的动力反应特征就会变化,在一定程度上会引起结构的模态特征发生改变[5-6]。因此,可以借助损伤前后频率的变化来判断结构是否发生损伤,该方法不失为一种最为简单而且最为实用的方法[7-9]。

结构损伤识别有4个目标：1) 判断结构损伤的存在;2) 判断结构损伤发生的位置;3) 确定结构损伤的程度;4) 预估结构的剩余寿命。目前，关于结构损伤存在与否的判定技术已较完善,而对于损伤识别的第二层次和第三层次是研究的关键和难点。运用曲率法多重损伤检测近几年正在逐渐成为研究的热点。然而，关于结构损伤识别的研究主要集中在大型钢和梁结构中，对压电陶瓷损伤识别的研究却非常少。

模态分析可以确定一个结构或机构的固有频率和振型。应用ANSYS所进行的模态分析大都是基于线性系统的,忽略了其非线性因素。经过ANSYS分析计算得出的结论是：运用模态位移是无法区分损伤单元的。实际上,位移模态对结构的局部损伤并不敏感,当结构的某一构件发生小损伤,其刚度有可能被削弱,但是这可能对结构的整体刚度影响不大,主要由于结构内部各构件间相互影响,限制了结构整体信息的改变。

曲率为振型位移的二阶导数，当结构发生损伤时，可以较明显地体现在模态振型曲率的变化上。

结构的曲率模态振型是位移模态振型的二阶导数，在结构有限元离散模型的振动模态分析中，若已知等间距的离散单元节点的位移模态振型，可以通过中央差分公式近似地求出结构的曲率模态振型：

其中：i为节点的位置，j为模态振型的阶数，φi+1,j,φi-1,j为相邻两节点的振幅，h为相邻两节点的距离。结构损伤前后的振型幅值分别为φi,j,φdi,j，幅值变化量Δφi,j=φdi,j-φi,j，即结构的振型变化曲率值为：

本文应用有限元软件对压电陶瓷片进行结构损伤的仿真模拟,讨论通过模态曲线值以及模态振型曲率差是否可以识别压电片的损伤，考察不同方法对压电片损伤程度的识别效果，从而确定该损伤定位方法的适用范围。损伤识别主要从两方面，一方面是对单处受伤的压电片损伤识别分析；另一方面是对多处受伤的压电片损伤识别分析。

2 压电陶瓷片的有限元模型

压电材料由于在力学变形与电学效应方面具有显著的耦合特性，近年来已在各种传感器和机敏结构中得到广泛的应用。通过对ANSYS的学习和研究，发现ANSYS单元库中的SOLID5单元可用于磁、热、电、压电和结构场之间的三维耦合分析。SOLID5单元具有8个结点,每个结点具有6个自由度。当应用于压电分析时，SOLID5单元具有大变形能力,此时其温度和磁场自由度不作计算，本文选用SOLID5单元作为压电陶瓷片划分网格的单元类型。

压电陶瓷片模型简化为长30 mm，宽7 mm，高3 mm的长方体。利用ANSYS对压电陶瓷片进行模态分析时，需输入压电陶瓷的材料参数，主要包括密度和3大矩阵：介电常数矩阵、弹性刚度常数矩阵和压电常数矩阵。 密度选为7 600 kg/m3。

介电常数矩阵[ε]×10-9(F/m):

压电常数矩阵[e] ×10-11(C/m2)：

弹性刚度常数矩阵e-12:

ANSYS里运用SWEEP方式对该结构划分成40个单元网格。如图1所示，从左往右分别称之为第1到第40个单元。

图1 压电陶瓷片有限元图

对于结构某一位置的损伤模拟,采用保持结构单元截面不变,即不改变单元质量,利用单元抗弯刚度的降低来模拟结构的损伤。不同损伤程度用单元抗弯刚度折减的百分比来表示,即：

式中:(EI)u表示未损伤的抗弯刚度,(EI)d表示有损伤的抗弯刚度,i表示单元号。

本文中研究单元损伤1/5、1/2、4/5三种情况下的曲率模态特性，即是分别将弹性刚度常数矩阵乘以1/5、1/2、4/5三种系数，然后选择此参数对相应的单元重新划分网格，使之具有相对应的损坏特性。

3 损伤位值识别

1) 单处损伤

建立2个有限元模型，设置第20个单元和第32个单元分别受损，其损伤程度相同，计算后显示其曲率模态曲线如图2。

图2说明无论是低阶还是高阶模态特性，22单元和32单元的单处损伤位置分别准确地反映在相对应的曲率曲线上，这将有助于损伤位置的识别与鉴定。

2) 多处损伤

如图3所示，第1个有限元模型设定第12单元和32单元受损，第2个有限元模型设置第12、22、32单元受损。其受损程度都一样，考虑其四阶曲率模态，经过计算，结果表明该曲线能够准确地识别多处损伤。

由基于振型曲率差模态对压电片损伤位置的识别结果可知，该方法既可以在单处损伤处识别损伤，也可以在多处受损的位置进行识别，四阶曲率曲线都能很好地反映损伤特性，但是由于现实中第一、第二阶比较能够容易得到，所以仿真结果只取低阶曲率特性曲线就足够了。

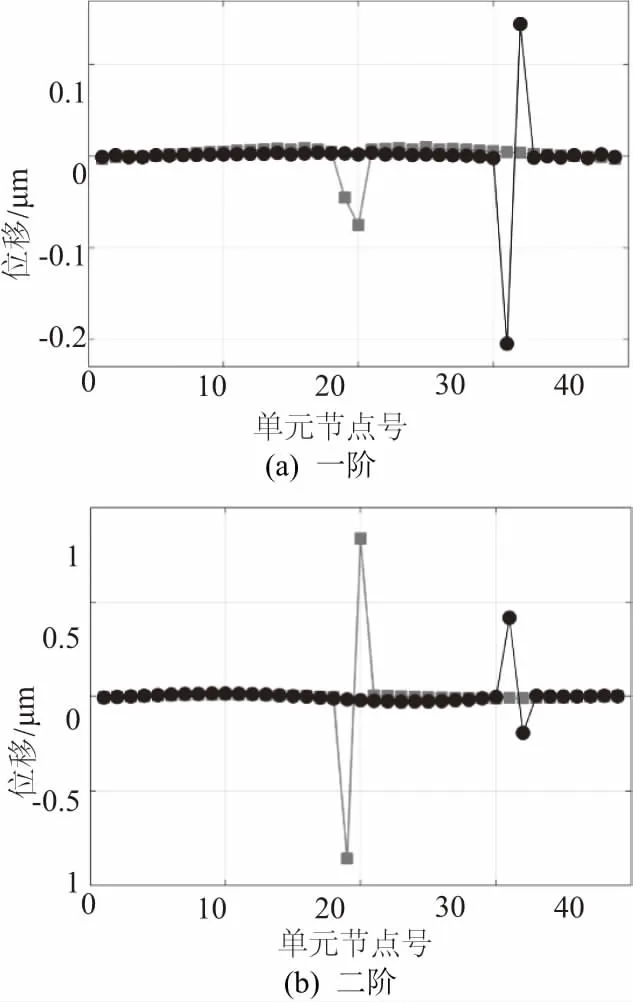
图2 单处受损位置识别结果

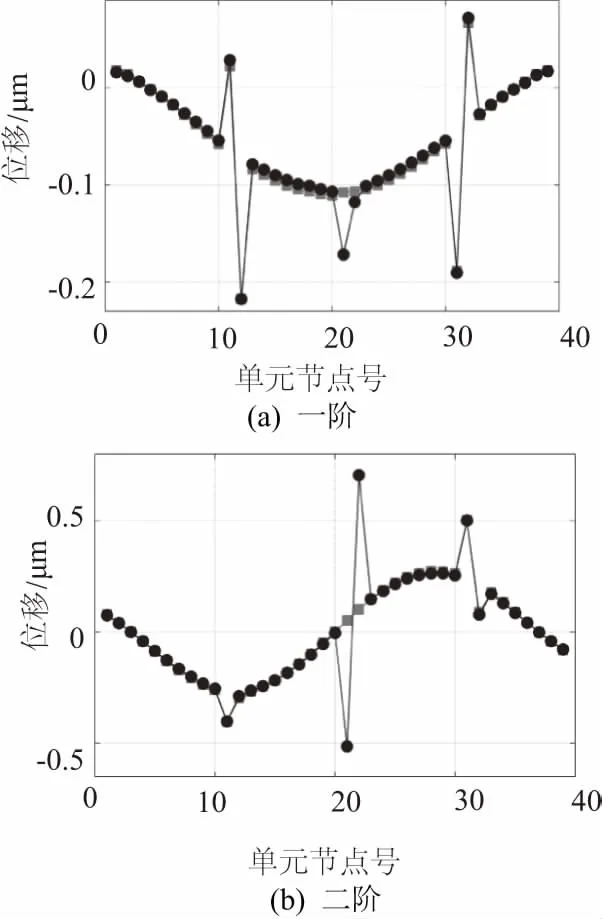
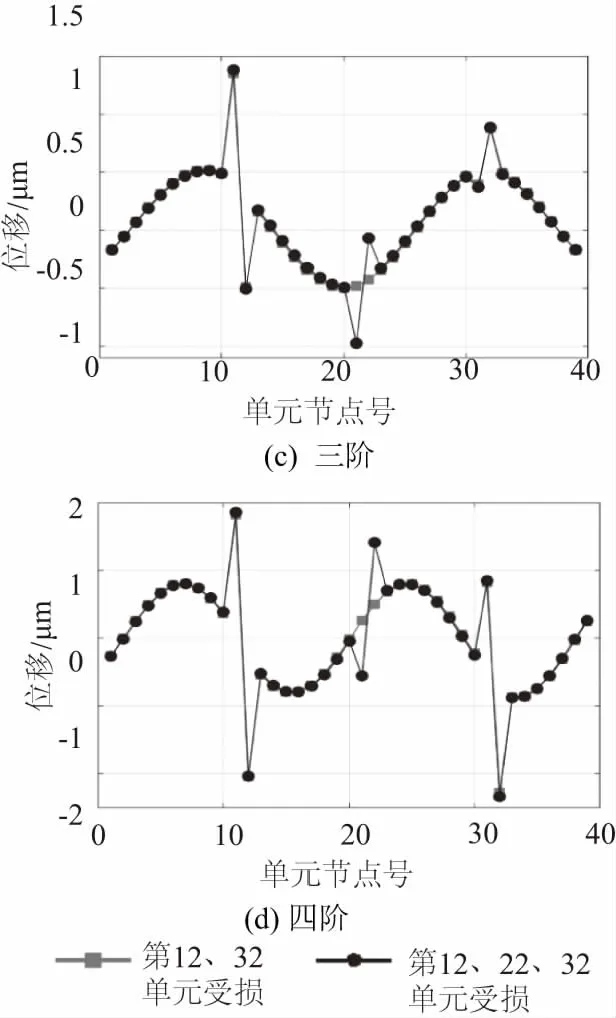
图3 多处受损位置识别结果

4 损伤程度识别

图4显示的是20单元受损1/5、1/2、4/5的情况下，其第一阶和第二阶的曲率特性曲线。这两阶特性曲线表明，损伤程度越高，突变的峰值也越高。图5则说明两阶特性曲线不仅仅适用于单处损伤程度的识别，还适用于多处损伤程度的识别。

图4中一阶曲线损伤处振幅最大值仅为0.1，二阶曲线振幅最大值达到1。图5中同样说明二阶曲率曲线损伤处的振幅比一阶曲线相同的位置要明显。

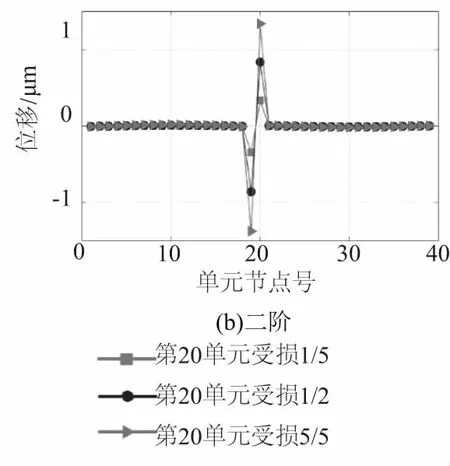
图4 单处受损不同程度识别

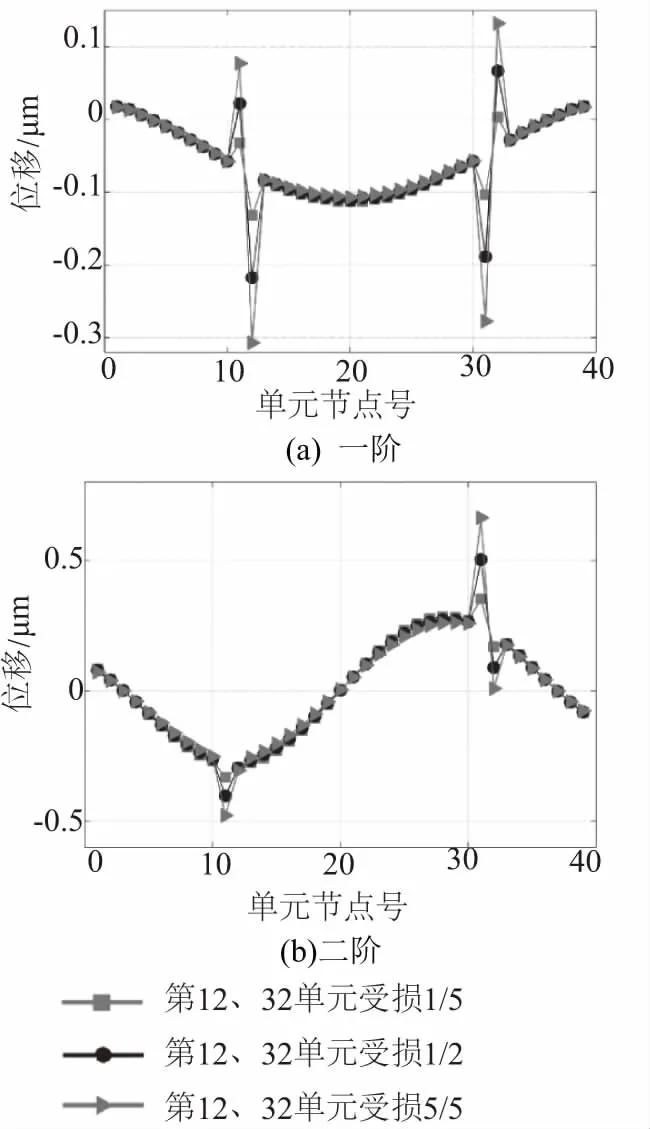
图5 两处受损不同程度识别

5 结语

模态值无法鉴别损伤特性，而曲率模态法对结构损伤较为敏感，运用曲率模态法对单处损伤、多处损伤的位置进行了分析确定。曲率模态曲线还能鉴别单、多处损伤的程度，曲线突变的程度能识别结构损伤的程度。应用曲率模态绘制出曲率模态的曲线，观察图形的突变情况判断损伤位置与程度。

1) 曲率模态曲线可以识别陶瓷片单处以及多处的损伤位置。

2) 随着损伤程度的加深，模态曲率曲线故障处的振幅也将会发生相对应的变化。说明了该方法也可以识别陶瓷片的损伤程度。

3) 与一阶曲率特性曲线相比，二阶曲线的效果更明显。

陶瓷片的曲率模态曲线可以把故障的损伤程度以及位置完美地显示出来，以后将会运用实验对这种方法进行验证。

参考文献:

[1] 刘增华，王娜，何存富，等. 基于压电陶瓷片的Lamb 波单模态激励及缺陷检测的实验研究[J]. 北京工业大学学报，2011,37(10)：1453-1458.

[2] 姜德义，郑拯宇，李林，等. 压电陶瓷片耦合振动模态的ANSYS模拟分析[J]. 传感技术学报，2003,16(4):452-456.

[3] 王锋. 应变模态分析在机械结构损伤检测中的应用[D]. 太原:太原理工大学，2011.

[4] Xiong Xiaoyan,Wang Feng,ete.Structural Damage Detection Using PCA and ImProved FRF Curvature Method[C]. 2011Fourth International Conferenee on Intelligent ComPutation Teehnology and Automation.ICICI,A20ll:723-726.

[5] 梁磊,王少萍,曹锋. 基于ANSYS的压电陶瓷PLZT特性仿真分析[J]. 北京航空航天大学学报,2008,34(7):853-856.

[6] 孙杰. 基于多模态参数的桥梁结构损伤识别方法研究[D]. 武汉:武汉理工大学,2013.

[7] 赵忠华. 基于改进模态参数灵敏度法的结构损伤识别研究[D]. 重庆:重庆大学,2010.

[8] F.J. Arnold , S.S. Muhlen, The influence of the thickness of non-piezoelectric pieces on pre-stressed piezotransducers[J]. Ultrasonics, 2004,41(3):191-196.

[9] Sandris Rucevskis, Mezhlum A. Sumbatyan, Tikhonov’s regularization approach in mode shape curvature analysisapplied to damage detection[J]. Mechanics Research Communications, 2015,65:9-16.