中低速磁浮列车-简支梁系统耦合振动试验研究

耿 杰，王党雄，李小珍，邱晓为

(1.西南交通大学 土木工程学院，四川 成都 610031；2.中铁第四勘察设计院集团有限公司，湖北 武汉430063)

中低速磁浮交通作为一种新兴的交通方式，因诸多优点受到人们的关注[1]。长沙中低速磁浮交通作为我国第一条拥有完全自主知识产权的中低速磁浮线路，已于2016年5月6日成功实现商业运营。目前，国内外诸多城市亦在建设或规划建设中低速磁浮交通。

中低速磁浮列车通过主动调节有源控制的电磁悬浮力，使磁浮列车保持在额定悬浮间隙(8～10 mm)附近，从而实现平稳运行。中低速磁浮列车运行速度较低(小于120 km/h)，所需的横向导向力较小，故横向无独立的主动导向控制，该导向力一般由悬浮电磁铁提供，在横向实现导向自稳定[1]。因此，实时调节悬浮间隙是磁浮列车实现平稳运行的关键。预应力混凝土简支梁是磁浮线路中较常用的梁型，在磁浮列车的作用下，简支梁会产生变形，影响悬浮间隙，从而影响车辆的平稳运行[2]。与轮轨交通一样，存在明显的磁浮车辆-桥梁系统耦合振动效应，该系统具有明显的时变特性。国内外学者针对磁浮车辆-桥梁系统耦合振动，进行了诸多研究。文献[3]将磁浮车体简化为两自由度悬挂系统，考虑PI神经网络悬浮控制，桥梁采用模态综合法，探讨列车在简支梁上运行时的共振效应及悬浮控制参数对耦合振动响应的影响。文献[4]建立5自由度磁浮车辆模型，探讨考虑和不考虑耦合振动时，车体及桥梁结构动力响应的差异，研究车辆5个自由度分别进行激扰时，对耦合动力响应的影响，结果表明：考虑耦合振动时系统对各自由度的激扰更敏感。文献[5]建立10自由度的TR06磁浮列车模型，将悬浮控制简化为线性弹簧阻尼系统，探讨随机轨道不平顺激励下磁浮列车-高架桥系统的竖向耦合振动特性。文献[6]建立高速磁浮车辆-桥梁系统的空间耦合振动模型，采用PID反馈控制，桥梁采用有限元法，探讨存在和不存在随机不平顺激扰时系统各动力响应的频谱分布规律。文献[7]基于传递函数法，对悬浮控制系统进行了细致探讨。文献[8-10]分析悬浮控制系统、弹性桥梁的动态特性。文献[10-13]建立磁浮列车-桥梁系统的垂向耦合振动模型，分析桥梁刚度、材料和结构形式对磁浮列车-桥梁系统动力响应的影响。文献[14]分析线路不平顺对高速磁浮铁路动力响应特性的影响。文献[15-16]探讨了风荷载对磁浮列车-桥梁系统耦合振动的影响。

以上文献从理论分析角度对磁浮列车-桥梁系统的耦合振动进行了细致分析，得出了诸多有意义的结论。本文基于目前已开通运营的长沙中低速磁浮交通运营线，以其中一孔25 m简支梁为研究对象，进行现场动载试验，从试验角度对中低速磁浮列车-桥梁系统的耦合振动进行研究，探讨系统各动力响应及变化规律，以期为中低速磁浮列车-简支梁系统耦合振动的理论分析及工程设计提供参考。

1 试验概况

1.1 试验段简介及参数

长沙中低速磁浮交通运营线起于长沙火车南站，止于长沙黄花机场，线路全长18.643 km，双线设计，线间距为4.4 m，其中高架桥区间占线路总长的86.3%。车辆采用五模块中低速磁浮列车(共有5对悬浮侧架)，三节编组，设计定员车辆总质量为(30+30+30) t，设计最高运营速度为100 km/h。

图1为线路高架段典型25 m预应力混凝土简支梁跨中横截面，计算跨径为24.2 m。左右两幅箱梁采用横隔板横向连接，横隔板纵向间距6 m，厚0.3 m。单幅箱梁高2.1 m，底板宽1.4 m，顶板宽1.3 m，顶板厚0.22 m，腹板厚0.26 m，底板厚0.30 m。采用C50混凝土，单线二期恒载20 kN/m。墩高11.25 m，采用矩形截面。桥上轨道部分由承轨台、扣件、钢轨枕、F轨组成，F轨纵向支撑间距为1.2 m，如图2所示。

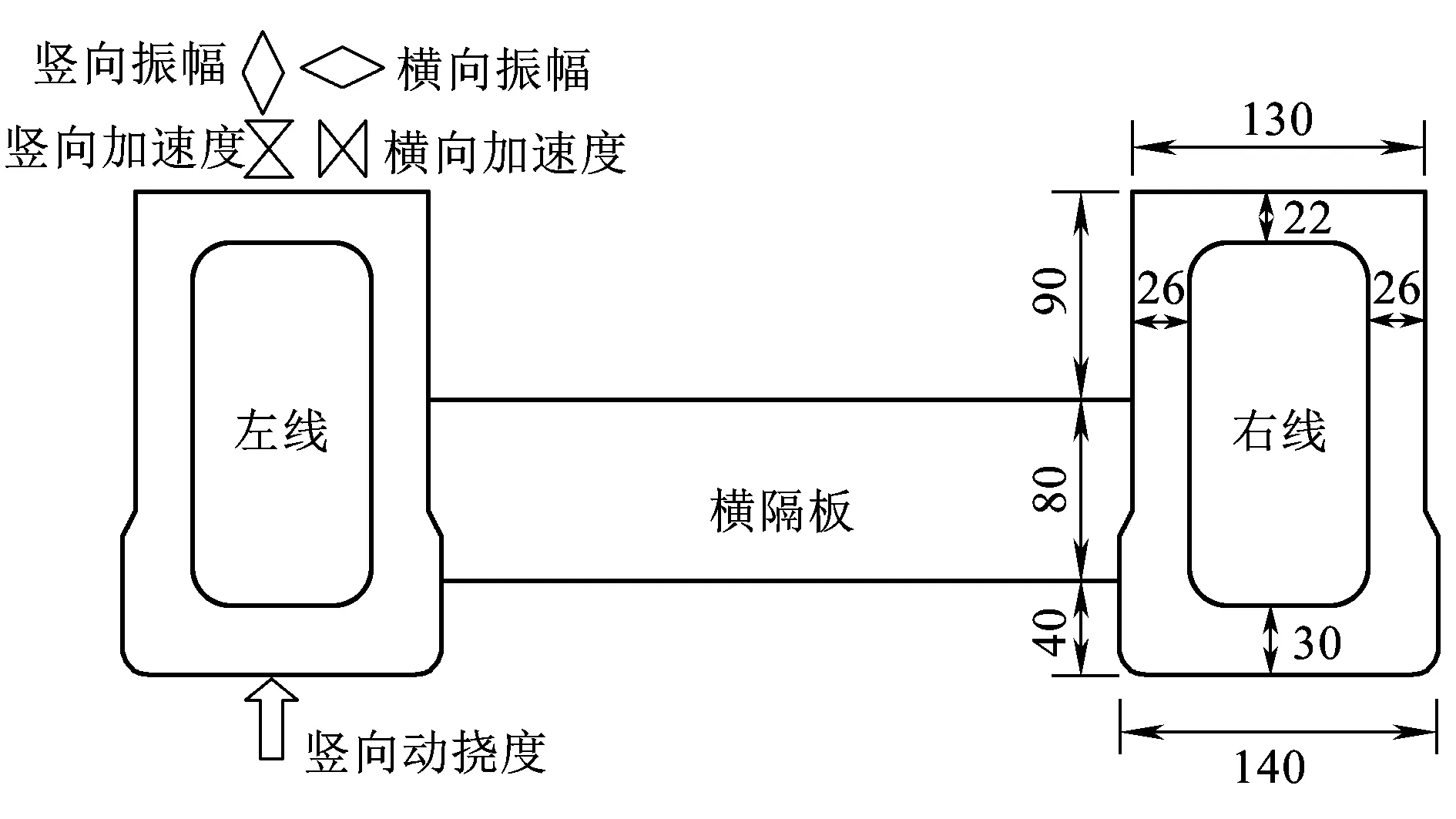
图1 25 m简支梁跨中截面尺寸及测点布置(单位：cm)

图2 轨道结构尺寸(单位：cm)

1.2 试验设计

本次试验选取其中的一孔25 m双线简支梁为测试对象。测试速度范围为10～100 km/h，级差为10 km/h，每个速度级下测试工况不少于3组。测试项目及测点位置见表1，选取一列磁浮列车中的2号车辆测试，车体加速度测点布置在2号车辆前部即1号悬浮侧架上方对应的车体地面板，悬浮侧架测点布置在1号悬浮侧架处。桥梁测点布置如图1所示，均布置于左线简支梁。图3为车体及悬浮侧架的测点布置。

表1 测点布置

图3 车体及悬浮侧架振动加速度测点布置

桥梁加速度及振幅均采用891-Ⅱ型拾振器测定(采样频率1 024 Hz)，车体加速度采用891-Ⅱ型拾振器测定(采样频率512 Hz)，悬浮侧架加速度采用CA-YD -188压电式加速度传感器测定(采样频率为1 024 Hz)，桥梁跨中竖向动挠度用百分表测定(采样频率100 Hz)。动挠度采用TML DRA-30A动静态应变仪进行数据采集，其他均采用INV3060S 24位智能采集仪进行数据采集。图4为现场试验照片。

(a)磁浮车辆 (b)车体加速度测点布置

(c)悬浮侧架加速度测点布置 (d)简支梁加速度、振幅测点布置 图4 现场试验照片

2 桥梁的动力响应分析

2.1 动挠度

图5为速度80 km/h时简支梁跨中竖向动挠度时程曲线。从图5可以看出，简支梁跨中动挠度经历磁浮列车上桥、桥上运行、出桥三个阶段，最大跨中动挠度为1.688 mm，远小于《长沙磁浮交通工程设计暂行规定》(Q/HNCFGS 001—2015)中桥梁竖向挠度限值L/4 600(L为桥梁计算跨径)。

图5 简支梁跨中竖向动挠度时程曲线

图6与图7分别为简支梁跨中竖向动挠度最大值和动力系数随速度的变化规律，表2和表3分别为对应的测试数据。从图6、图7与表2、表3可以看出，随着速度增加，竖向动挠度最大值与动力系数整体上均逐渐增大。动挠度最大值随车速的变化率为0.000 14 mm/(km/h)，变化率较小，拟合度R2为0.118，线性拟合效果较差。动力系数随车速的变化率为0.000 085/(km/h)，拟合度R2为0.592，线性拟合效果较好，最大动力系数约为1.022(100 km/h运行时)，动力系数较小，满足《长沙磁浮交通工程设计暂行规定》(Q/HNCFGS 001—2015)中桥梁动力系数小于1.15的规定。

图6 简支梁跨中竖向动挠度随速度变化情况

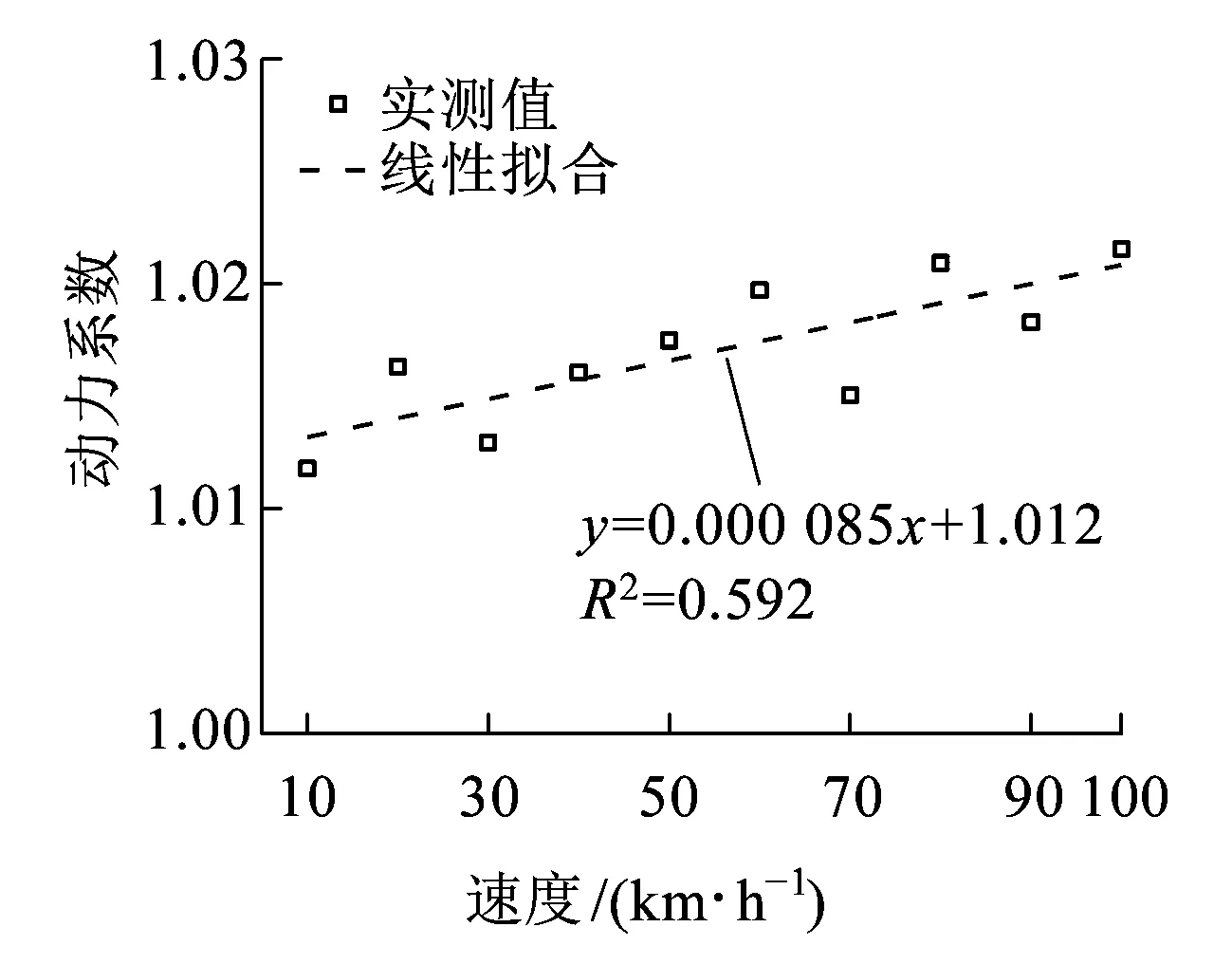
图7 简支梁动力系数随速度变化情况

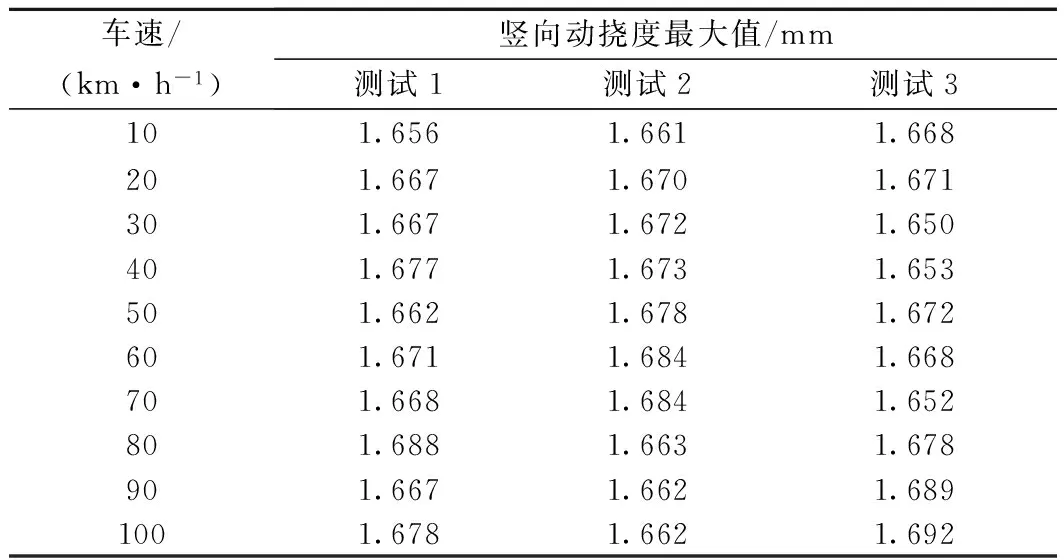
车速/(km·h-1)竖向动挠度最大值/mm测试1测试2测试3101.6561.6611.668201.6671.6701.671301.6671.6721.650401.6771.6731.653501.6621.6781.672601.6711.6841.668701.6681.6841.652801.6881.6631.678901.6671.6621.6891001.6781.6621.692

表3 不同速度工况简支梁动力系数

2.2 振动加速度

图8为速度80 km/h，简支梁跨中竖向(参考《高速铁路设计规范》[17]规定，低通20 Hz滤波)与横向(参考《欧洲ENV 1991-3规范》规定，低通40 Hz滤波)振动加速度时程曲线。从图8可知，桥梁跨中竖向与横向最大振动加速度值分别为0.192、0.065 m/s2，满足规范要求：竖向加速度小于5.0 m/s2(《高速铁路设计规范》[17]，无砟桥面)，横向加速度小于1.4 m/s2(《铁路桥梁检定规范》[18])。简支梁竖向振动加速度明显大于横向，这是由于中低速磁浮列车运行速度较低，横向导向力较小，且为双线简支梁，横向刚度比竖向刚度大。

(a)竖向振动加速度

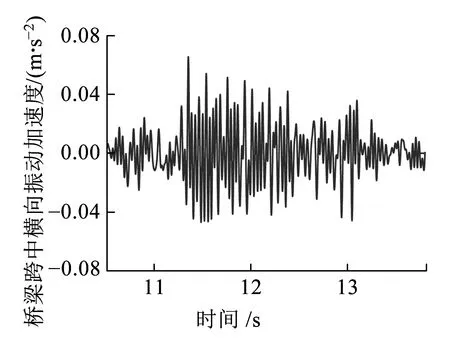
(b)横向振动加速度图8 简支梁跨中振动加速度时程曲线

图9为简支梁跨中竖向与横向加速度随车速的变化规律，表4为多次测试工况下对应的试验数据。从图9、表4可以看出，竖向与横向振动加速度均随车速的增加而增大；竖向与横向加速度随车速的变化率分别为0.001 4、0.000 54 m/s2/(km/h)，拟合度R2分别为：0.791、0.424，竖向线性拟合效果比横向好；竖向加速随车速的变化率较横向大，这是因为中低速磁浮列车车致桥梁结构振动主要为竖向振动，横向导向力小，横向振动较小。

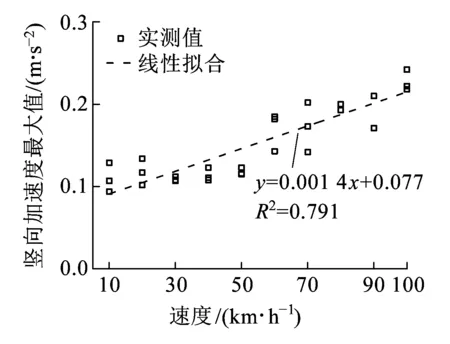
(a)竖向振动加速度

(b)横向振动加速度图9 简支梁跨中加速度随速度变化情况

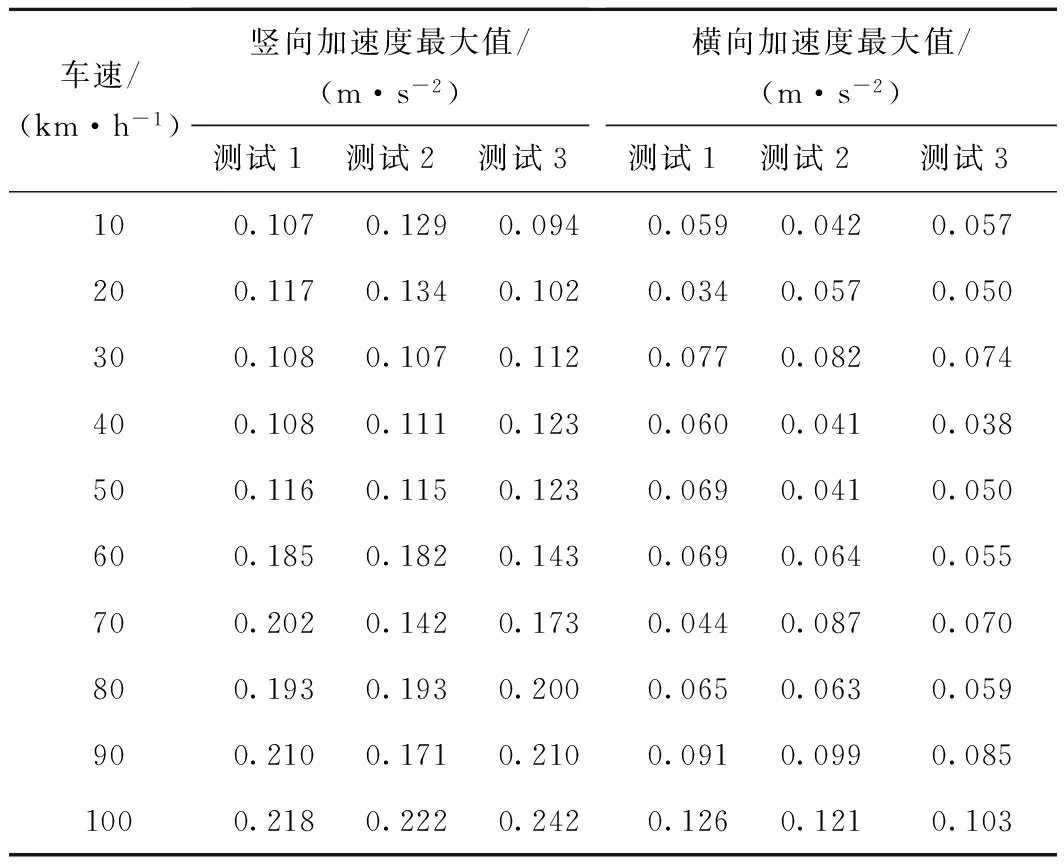
车速/(km·h-1)竖向加速度最大值/(m·s-2)测试1测试2测试3横向加速度最大值/(m·s-2)测试1测试2测试3100.1070.1290.0940.0590.0420.057200.1170.1340.1020.0340.0570.050300.1080.1070.1120.0770.0820.074400.1080.1110.1230.0600.0410.038500.1160.1150.1230.0690.0410.050600.1850.1820.1430.0690.0640.055700.2020.1420.1730.0440.0870.070800.1930.1930.2000.0650.0630.059900.2100.1710.2100.0910.0990.0851000.2180.2220.2420.1260.1210.103

为了进一步分析简支梁的振动特性，图10给出了速度80 km/h时多次测试工况下简支梁竖向与横向振动加速度频谱曲线。从图10可以看出：3次测试工况下简支梁竖向与横向振动加速度频谱曲线较一致，这也说明了测试数据的可靠性；竖向振动加速度的优势频段集中在20 Hz以内，最大峰值对应的频率点为7.0 Hz(简支梁一阶整体竖弯频率)，满足《长沙磁浮交通工程设计暂行规定》(Q/HNCFGS 001—2015)中桥梁设计的竖向一阶固有频率不小于90/L(L为桥梁计算跨径)的规定，在20 Hz以后竖向加速度均较小；横向加速度的优势频段与竖向相比较宽，集中于20～80 Hz，与竖向加速度相比，属于中高频振动。由于试验梁为双线简支梁，横向刚度较大，导致横向振动加速度优势频段的频率较大。

(a)竖向振动加速度

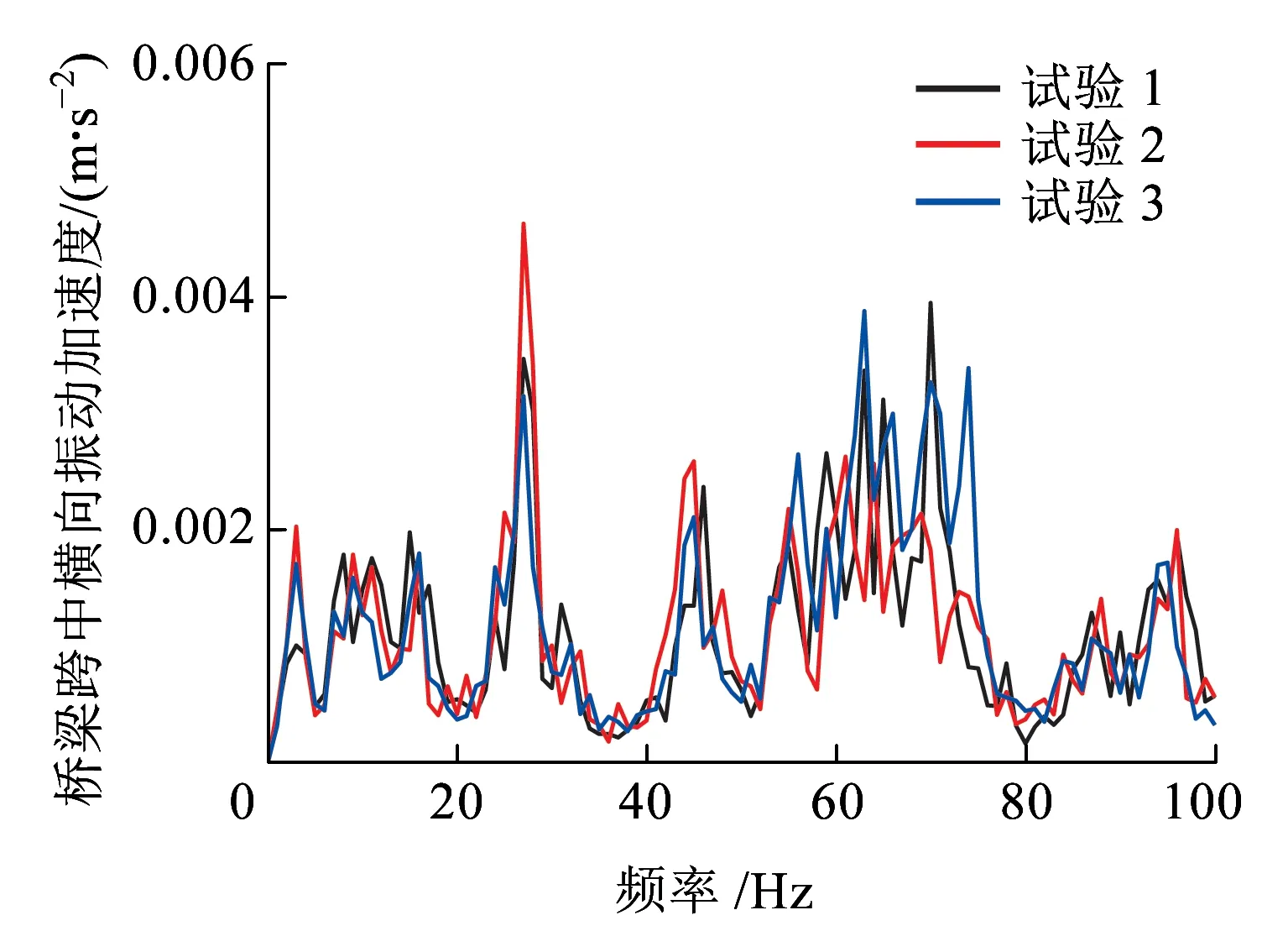
(b)横向振动加速度图10 简支梁跨中振动加速度频谱

2.3 振幅

图11为速度80 km/h时简支梁跨中竖向与横向振幅时程曲线。从图11可知，简支梁跨中竖向与横向振幅最大值分别为0.313、0.054 mm，竖向振幅远大于横向，均满足规范要求：竖向0.500 mm(《高速铁路桥梁运营性能检定规定(试行)》[19])，横向0.304 mm(《铁路桥梁检定规范》[18])。与竖向振幅相比，横向振幅波动更剧烈。由图10的分析可知，简支梁横向刚度比竖向刚度大，横向振动为中高频振动(20～80 Hz)，而竖向振动主要为低频振动(20 Hz以内)，因此，简支梁跨中横向振幅较竖向振幅变化剧烈，但幅值小。

(a)竖向振幅

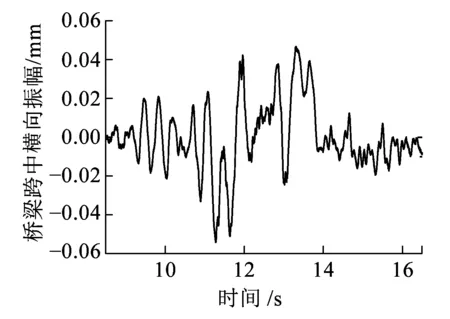
(b)横向振幅图11 简支梁跨中振幅时程曲线

图12为简支梁跨中竖向与横向振幅最大值随车速的变化规律，表5为多次测试工况下对应的试验数据。从图12、表5可以看出，随着车速增加，简支梁跨中竖向与横向振幅最大值均增加；竖向与横向振幅最大值的变化率分别为0.003、0.000 59 m/s2/(km/h)，拟合度R2分别为：0.982、0.859，线性拟合效果均较好。竖向振幅最大值的变化率较横向大，这是由于中低速磁浮列车横向导向力明显小于竖向电磁悬浮力，且简支梁横向刚度较大。

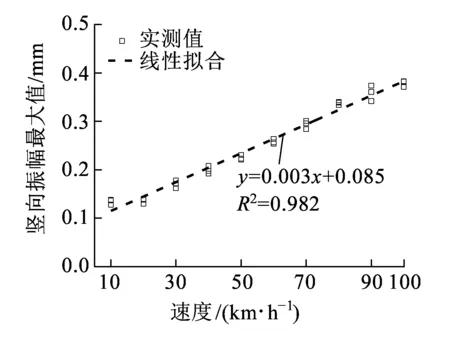
(a)竖向振幅

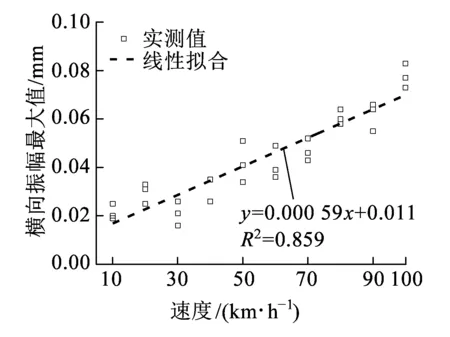
(b)横向振幅图12 简支梁跨中振幅随速度变化情况

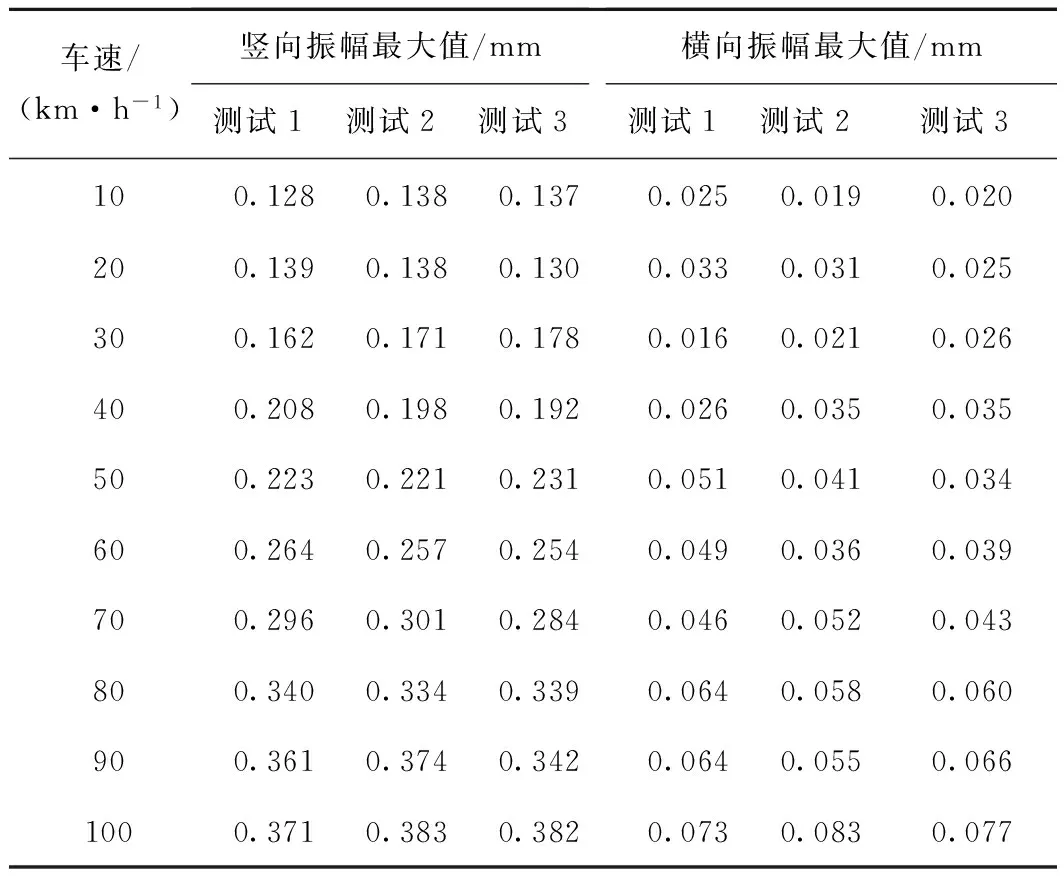
车速/(km·h-1)竖向振幅最大值/mm测试1测试2测试3横向振幅最大值/mm测试1测试2测试3100.1280.1380.1370.0250.0190.020200.1390.1380.1300.0330.0310.025300.1620.1710.1780.0160.0210.026400.2080.1980.1920.0260.0350.035500.2230.2210.2310.0510.0410.034600.2640.2570.2540.0490.0360.039700.2960.3010.2840.0460.0520.043800.3400.3340.3390.0640.0580.060900.3610.3740.3420.0640.0550.0661000.3710.3830.3820.0730.0830.077

需要指出，由于随机轨道不平顺谱的存在，列车在没有到达该25 m简支梁位置时已受到轨道不平顺谱的激励，已有动力响应。磁浮线路较长(18.643 km)，每一次测试时，即使在运行车速不变的情况下，列车即将在所测简支梁上运行时的初始动力响应也会不同。因此，每一次测试磁浮列车在所测简支梁上运行时，简支梁的动力响应亦有差别，因此图6、图7、图9及图12的测试数据具有一定的离散性。

3 磁浮列车的动力响应分析

3.1 车体

图13为速度80 km/h时车体竖向与横向加速度时程曲线。从图13可以看出：车体竖向、横向加速度最大值分别为0.335、0.289 m/s2，竖向加速度略大于横向，均满足《高速铁路设计规范》[17]中关于车体加速度应小于1.0 m/s2(竖向)、0.6 m/s2(横向)的规定。

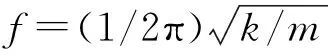
(a)竖向加速度

(b)横向加速度图13 车体加速度时程曲线

(a)竖向加速度

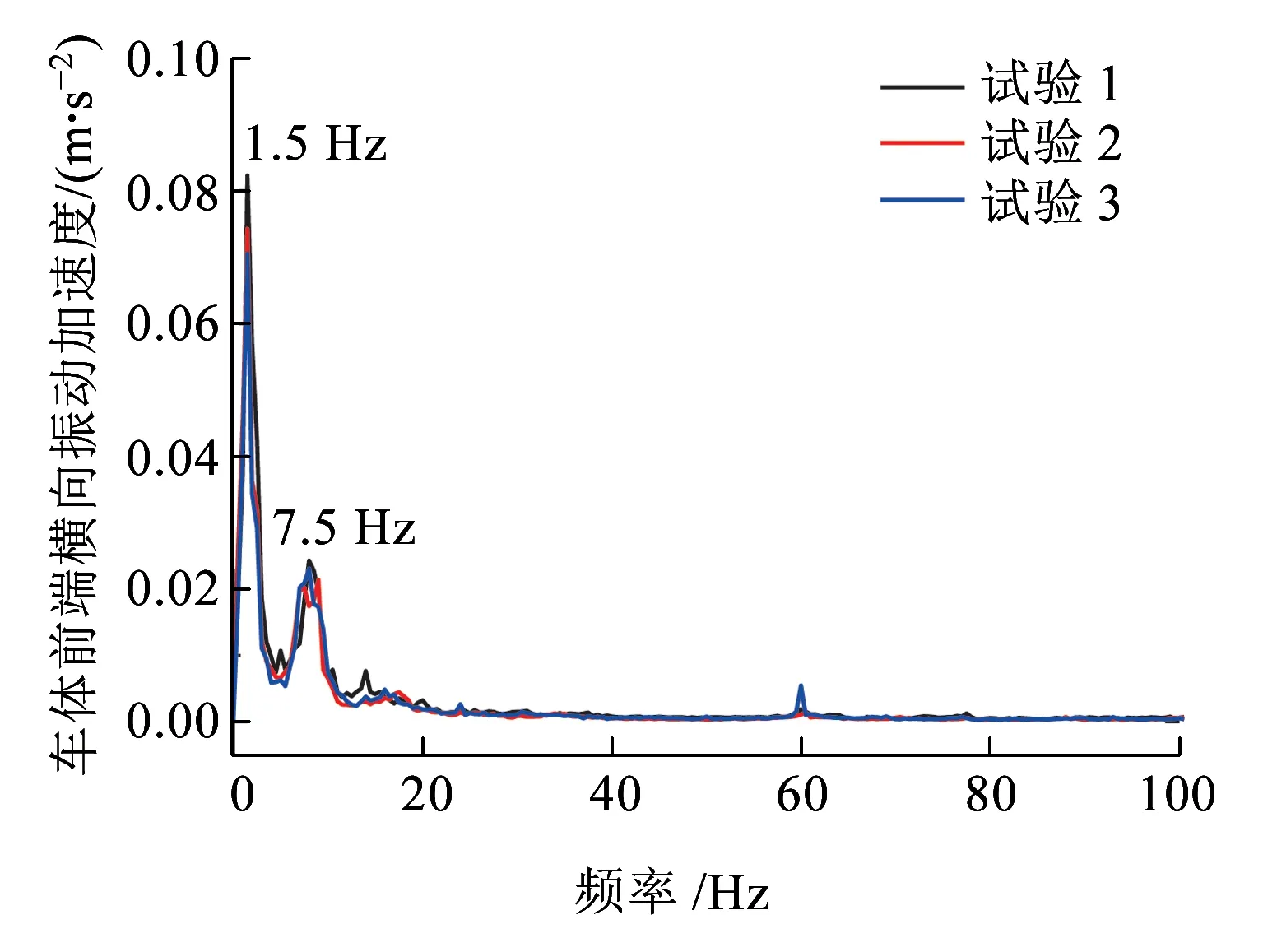
(b)横向加速度图14 车体加速度频谱

3.2 悬浮侧架

图15为速度80 km/h时，悬浮侧架竖向与横向加速度时程曲线。从图15可以得出，悬浮侧架竖向与横向加速度的最大值分别为3.071、2.131 m/s2，竖向加速度明显大于横向加速度，悬浮侧架的加速度明显大于车体加速度。

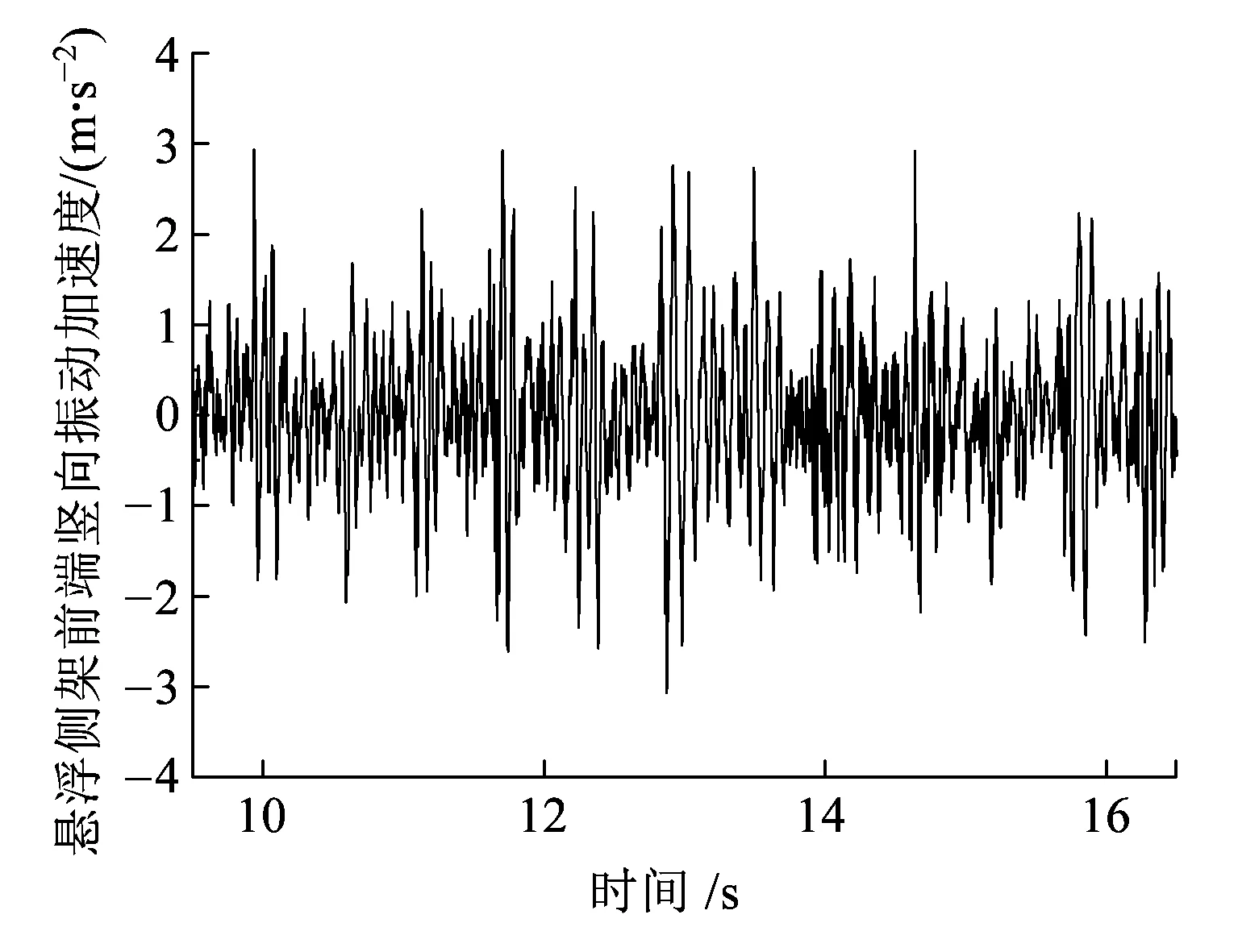
(a)竖向加速度

(b)横向加速度图15 悬浮侧架加速度时域图

图16为悬浮侧架加速度频谱曲线。从图16可以看出，与车体加速度相比，悬浮侧架加速度的优势频段均集中于20 Hz以内，频率分布较广泛，包含较显著的高频振动成分。

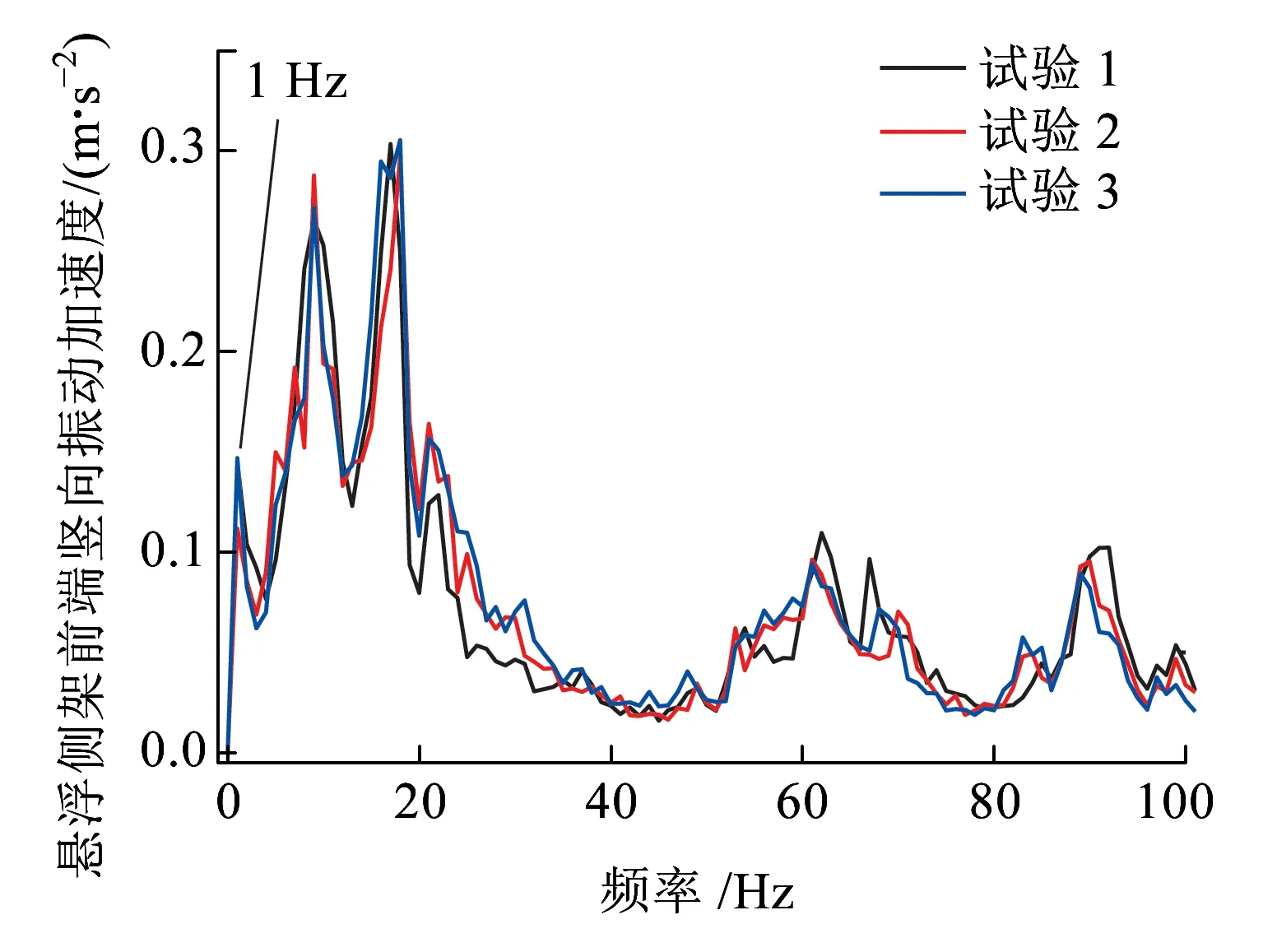
(a)竖向加速度

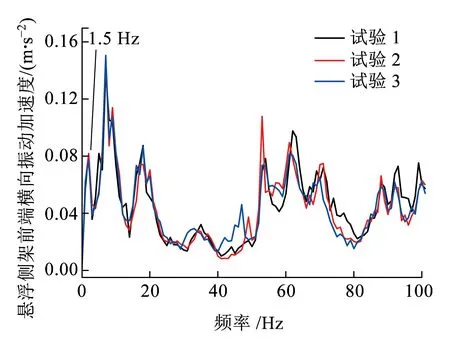
(b)横向加速度图16 悬浮侧架加速度频谱

4 结论

本文以长沙中低速磁浮交通运营线中的一跨25 m简支梁为研究对象，采用现场试验方法探讨磁浮列车在简支梁上运行时车辆-桥梁系统的耦合振动特性，得出以下结论：

(1)简支梁、车辆的动力性能均满足规范的设计要求，且动力响应值均较小，动力性能良好。随着车速的增加，简支梁各动力响应值均增大，且竖向各动力响应值的增速大于横向。

(2)中低速磁浮列车运营速度较小，横向导向力较小，且简支梁横向刚度较大，因此简支梁的横向动力响应远小于竖向。简支梁竖向振动的优势频段在20 Hz以内；简支梁横向加速度的优势频段集中于20～80 Hz，表现为中高频振动，因此横向振幅较竖向振幅变化更剧烈，但幅值较小。

(3)悬浮侧架横向与竖向加速度的优势频段均集中在20 Hz以内，同时也包含较显著的高频振动成分(50～100 Hz)；二系悬挂(空气弹簧)起到良好的隔振作用，将悬浮侧架传递到车体的高频振动能量隔掉，使得车体的振动加速度值较小，表现为低频振动(竖向1 Hz、横向1.5 Hz)。

(4)中低速磁浮交通有其自身的特点，应提出适合中低速磁浮交通的设计规范，合理指导设计。

参考文献：

[1]邓小星.中低速磁浮车辆系统动力学性能研究[D].成都:西南交通大学,2009.

[2]梁鑫,罗世辉,马卫华.常导磁浮列车动态磁轨关系研究[J].铁道学报,2013,35(9):39-45.

LIANG Xin,LUO Shihui,MA Weihua.Study on Dynamic Magnet-track Relationship of Maglev Vehicles[J].Journal of the China Railway Society,2013,35(9):39-45.

[3]YAU J D.Vibration Control of Maglev Vehicles Traveling over a Flexible Guideway[J].Journal of Sound and Vibration,2009,321(1/2):184-200.

[4]ZHENG X J,WU J J,ZHOU Y H.Numerical Analyses on Dynamic Control of Five-degree-of-freedom Maglev Vehicle Moving on Flexible Guideways[J].Journal of Sound and Vibration,2000,235(1):43-61.

[5]ZHAO C F,ZHAI W M.Maglev Vehicle/guideway Vertical Random Response and Ride Quality[J].Vehicle System Dynamics,2002,38(3):185-210.

[6]SHI J,WEI Q C,ZHAO Y.Analysis of Dynamic Response of the High-speed EMS Maglev Vehicle/guideway Coupling System with Random Irregularity[J].Vehicle System Dynamics,2007,45(12):1077-1095.

[7]GOODALL R M.Dynamic Characteristics in the Design of Maglev Suspensions[J].Journal of Rail and Rapid Transit,1994,208(1):33-41.

[8]翟婉明,赵春发.磁浮车辆/轨道系统动力学(Ⅰ):磁/轨相互作用及稳定性[J].机械工程学报,2005,41(7):1-10.

ZHAI Wanming,ZHAO Chunfa.Dynamics of Maglev Vehicle/guideway Systems(Ⅰ):Magnet/rail Interaction and System Stability[J].Chinese Journal of Mechanical Engineering,2005,41(7):1-10.

[9]赵春发,翟婉明.磁浮车辆/轨道系统动力学(Ⅱ):建模与仿真[J].机械工程学报,2005,41(8):163-175.

ZHAO Chunfa,ZHAI Wanming.Dynamics of Maglev Vehicle/guideway Systems(Ⅱ):Modeling and Simulation[J].Chinese Journal of Mechanical Engineering,2005,41(8):163-175.

[10]赵春发,翟婉明,蔡成标.磁浮列车/高架桥垂向耦合动力学研究[J].铁道学报,2001,23(5):27-33.

ZHAO Chunfa,ZHAI Wanming,CAI Chengbiao.Maglev Vehicle/elevated-beam Guideway Vertical Coupling Dynamics[J].Journal of the China Railway Society,2001,23(5):27-33.

[11]时瑾,魏庆朝,吴范玉.高速磁浮铁路轨道梁振动分析及控制研究[J].中国安全科学学报,2003,13(10):76-80.

SHI Jin,WEI Qingchao,WU Fanyu.Study on Vibration of the Beam of Magnetic Levitation Express Railway and Its Control[J].China Safety Science Journal,2003,13(10):76-80.

[12]姜卫利,高芒芒.轨道梁参数对磁浮车-高架桥垂向耦合动力响应的影响研究[J].中国铁道科学,2004,25(3):71-75.

JIANG Weili,GAO Mangmang.Study of the Effect of Track Beam Parameters on Vertical Coupled Dynamic Response of Maglev Vehicle-viaduct[J].China Railway Science,2004,25(3):71-75.

[13]LEE J S,KWON S D,KIM M Y,et al.A Parametric Study on the Dynamics of Urban Transit Maglev Vehicle Running on Flexible Guideway Bridges[J].Journal of Sound and Vibration,2009,328(3):301-317.

[14]时瑾,魏庆朝.线路不平顺对高速磁浮铁路动力响应特性的影响[J].工程力学,2006,23(1):154-159.

SHI Jin,WEI Qingchao.The Effect of Guideway Irregularity on the Dynamic Characteristics of High-speed Mag-lev Railway[J].Engineering Mechanics,2006,23(1):154-159.

[15]YAU J D.Aerodynamic Vibrations of a Maglev Vehicle Running on Flexible Guideways under Oncoming Wind Actions[J].Journal of Sound and Vibration,2009,329(10):1743-1759.

[16]KWON S D,LEE J S,MOON J W,et al.Dynamic Interaction Analysis of Urban Transit Maglev Vehicle and Guideway Suspension Bridge Subjected to Gusty Wind[J].Engineering Structure,2008,30(12):3445-3456.

[17]国家铁路局.TB 10621—2014 高速铁路设计规范[S].北京:中国铁道出版社,2015.

[18]中华人民共和国铁道部.铁路桥梁检定规范[S].北京:中国铁道出版社,2004.

[19]中国铁路总公司.高速铁路桥梁运营性能检定规定(试行)[S].北京:中国铁道出版社,2014.

[20]LI Z G,WU T X.Modelling and Analysis of Force Transmission in Floating-slab Track for Railways[J].Journal of Rail and Rapid Transit,2008,222(1):45-57.

[21]马大猷.噪声与振动控制工程手册[M].北京:机械工业出版社,2002.