基于实测应变的时域模态参与因子识别研究

胡伟钢，刘志明，王 曦，林浩博

(北京交通大学 机械与电子控制工程学院，北京 100044)

结构疲劳强度决定了机械系统的正常运转及使用寿命，且关系到飞机、铁路列车、汽车等交通工具的运行安全，在结构强度设计和运营评估中，了解结构的整体应变分布场和关键位置结构响应是十分必要的[1]。

结构响应一般分为非结构振动响应和结构振动响应[2]。铁道车辆部件对非结构振动响应测试一般采用直接测试法和准静态标定法[3-4]，对结构振动响应测试一般采用直接测试法[5-6]。目前，对于复杂结构振动响应测量一般是定性给出传感器布置方案[7-8]，在布置传感器过程中会有大量的经验性和不确定性。

本文提出一种通过优化结构表面可测部位测点的方法，逆求结构动态响应模态参与因子，获得结构整体应变响应。该方法利用应变片质量轻,在结构测试时不会改变被测结构动态参数的特点，通过在结构表面上粘贴合适数量的应变片，基于D优化理论优化最佳测点位置和方向，根据模态叠加基本原理，得到整体结构响应特征。该方法为复杂结构无法实测部位结构响应提供了一种间接测试方法。

1 模态参与因子估计基本理论

1.1 结构振动

对于一个结构可离散为N自由度的系统，其平衡运动方程为[9]

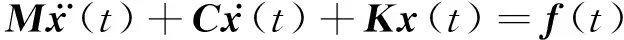
( 1 )

其中n×1的x(t)为结构振动响应。结构振动系统的振动响应可以表示为位移模态的线性组合。

( 2 )

式中：Φ=[φ1φ2…φn]，为n×n结构模态矩阵；qi(t)是模态振型φi的模态参与因子；q(t)=[q1q2…qn]为结构振型Φ模态参与因子向量。

在模态坐标下，结构运动方程可以表示为[10]

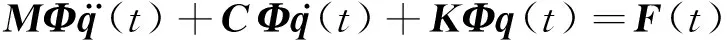
( 3 )

对于一个连续的结构体，在时域上结构变形与应变存在如下的线性微分关系

ε(t)=Dx(t)

( 4 )

式中：D是微分算子。通过微分运算对式( 2 )进行计算，对特定时间点模态的线性叠加为

( 5 )

结构模态的微分即为结构应变模态，根据式( 4 )、式( 5 )可以得到

( 6 )

式中：Ψε=[φ1φ2…φn]为结构模态应变矩阵。式( 6 )表明对于在线弹性范围内的小变形结构上任意点的时间域应变响应可以表示为模态应变的线性叠加，即模态叠加。

1.2 模态参与估计

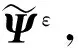
( 7 )

( 8 )

( 9 )

2 应变片测点布置方法

2.1 测试候选区

定义在结构表面上适宜安装应变片的所有区域为测试候选区，在测试候选区内可粘贴应变片测点为测试候选点，测试候选点与位置和方向有关，通过优化得到参与模态参与因子估计的测点组合为优化测点组。结合文献[3，8]所述的传感器布置方案及结构的几何特征，给出适宜布置应变片测试候选区的选择原则：

(1)测试候选区应充分反映结构弹性模态变形的整体特征，特别是结构的主要模态振动方向的变形。

(2)测试候选区必须保证本区域结构为弹性变形且应变梯度变化不应过大，这些区域包括载荷激励区、结构几何应力集中区、结构缺陷区等。

(3)测试候选区应避开应变片安装空间位置无法满足区域和传感器信号传输困难的区域，这些位置包括结构装配区域，如箱体内部、结构设计孔等。

在建立由实体单元离散的有限元模型时，利用薄膜单元在结构振动中只传递面内力，没有弯曲刚度的特点，在结构表面测试候选区域增加一层薄膜单元，通过薄膜单元应变信息来表达测试候选区的应变片信息。由于节点应变信息存在不唯一性，因此，选择单元应变信息进行分析计算。

测点方向θ是测点敏感度的变量，单元在不同角度θ(0°≤θ<180°)得到各自的应变张量，应变张量由xyz坐标系转化到任意x′y′z′坐标系[12]

式中：Tm是x′y′z′坐标系对xyz坐标系的转换矩阵。薄膜单元的局部坐标系内，z轴方向始终垂直于单元面，其转换矩阵为

2.2 D优化设计

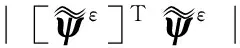
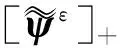
由优化矩阵[ψε]opt可得优化模态参与因子估计为

3 悬臂梁模态参与因子识别

3.1 激振悬臂梁有限元模型

将悬臂梁作为工程对象进行模态参与因子识别，搭建悬臂梁试验激振台，如图1所示，悬臂梁方形端后半部分固定，另一端开孔为激振杆装配孔，激振杆与悬臂梁之间为螺栓连接，激振器通过激振杆传递激振力。

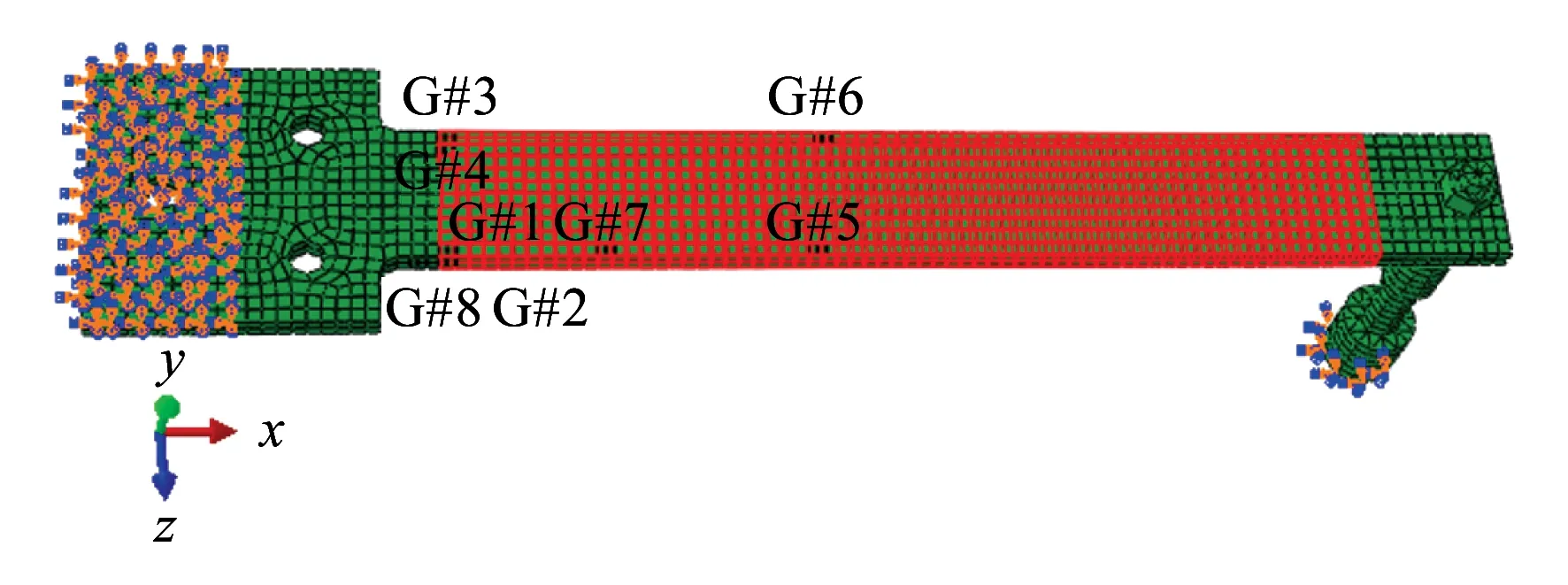
图1 试验悬臂梁

按照2.1节所述方法选择测试候选区，如图1中红色区域。对悬臂梁模型进行模态分析，表1为悬臂梁前3阶模态频率。

表1 试验悬臂梁前3阶模态频率

选择6个测点估计悬臂梁前3阶模态参与因子，按照2.2所述运用D优化法得到测试候选区内测点最佳位置和方向，图1中给出由测点G#1～G#6组成的优化测点组，预留候选区内部测点G#7和外部测点G#8验证模态参与因子估计。

图2所示为悬臂梁优化测点组G#1～G#6和验证测点G#7与G#8的前3阶模态应变矩阵。

图2 悬臂梁各测点前3阶模态应变矩阵

3.2 模态参与因子识别及验证

对激振器提供25～300 Hz的等幅值扫频信号，同步采集各应变片信号，采样频率为2 000 Hz，得到各测点的应变响应，根据式(13)，采用最小二乘法估计各阶模态参与因子，如图3所示。

图3 前3阶模态参与因子估计

根据上文的模态参与因子和模态应变矩阵，由式( 6 )模态叠加原理可得各测点应变响应时域波形。图4(a)和图5(a)所示分别为验证测点G#7和G#8的试验值和反求值时域波形。为了清晰表达时域波形的重合度，将试验信号和反求信号建立散点图，图4(b)和图5(b)所示分别为验证测点G#7和G#8的试验值和反求值的散点图。

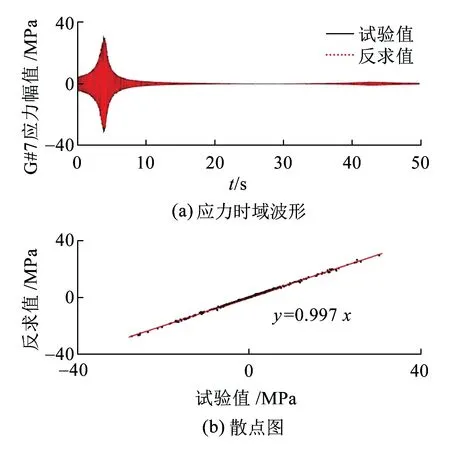
图4 测点G#7应力的试验值和反求值

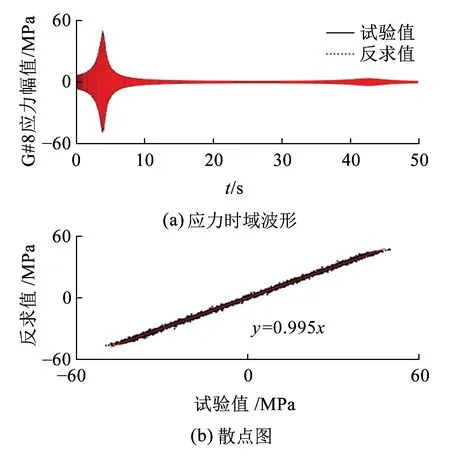
图5 测点G#8应力的试验值和反求值

表2所示为各测点试验值和反求值的散点拟合相关性及RMS误差，各测点线性拟合斜率接近1，相关性接近1，均方根误差均较小，说明试验应力信号和反求应力信号波形重合度高。验证测点G#7和G#8的散点图拟合斜率接近1，拟合相关性高，均方根误差小，反求波形和实际测试波形重合度高，说明运用模态参与因子估计的方法估计准确度高。

表2 各测点拟合相关性及RMS误差

4 箱体模态参与因子识别

4.1 箱体有限元模型

齿轮箱作为高速列车传动系统重要组成部分，对于保障高铁列车的动力传输具有重要作用，其主要由大小齿轮、箱体和联轴节构成，其中，小齿轮通过联轴节与牵引电机相连，大齿轮直接压装在轮轴上，齿轮箱箱体的一端通过抱轴承悬挂在车轴上，另一端通过吊杆吊挂在构架横悬臂梁上[15]。图6所示为齿轮箱箱体有限元模型，在箱体安装轴承的中心建立参考点RP1、RP2、RP3和RP4，吊饼区中心建立参考点RP5，箱体和轴承的接触面与对应参考点之间建立耦合关系，参考点RP5与吊饼面建立耦合关系，约束参考点RP5的Y和Y转动方向，箱体通过抱轴方式悬挂在车轴上，因此，约束参考点RP1和RP2的X、Y、Z、X转动和Y转动方向。

图6 齿轮箱箱体模型

对箱体进行模态分析，图7所示为第1阶模态应变响应，表3为前11阶模态频率。

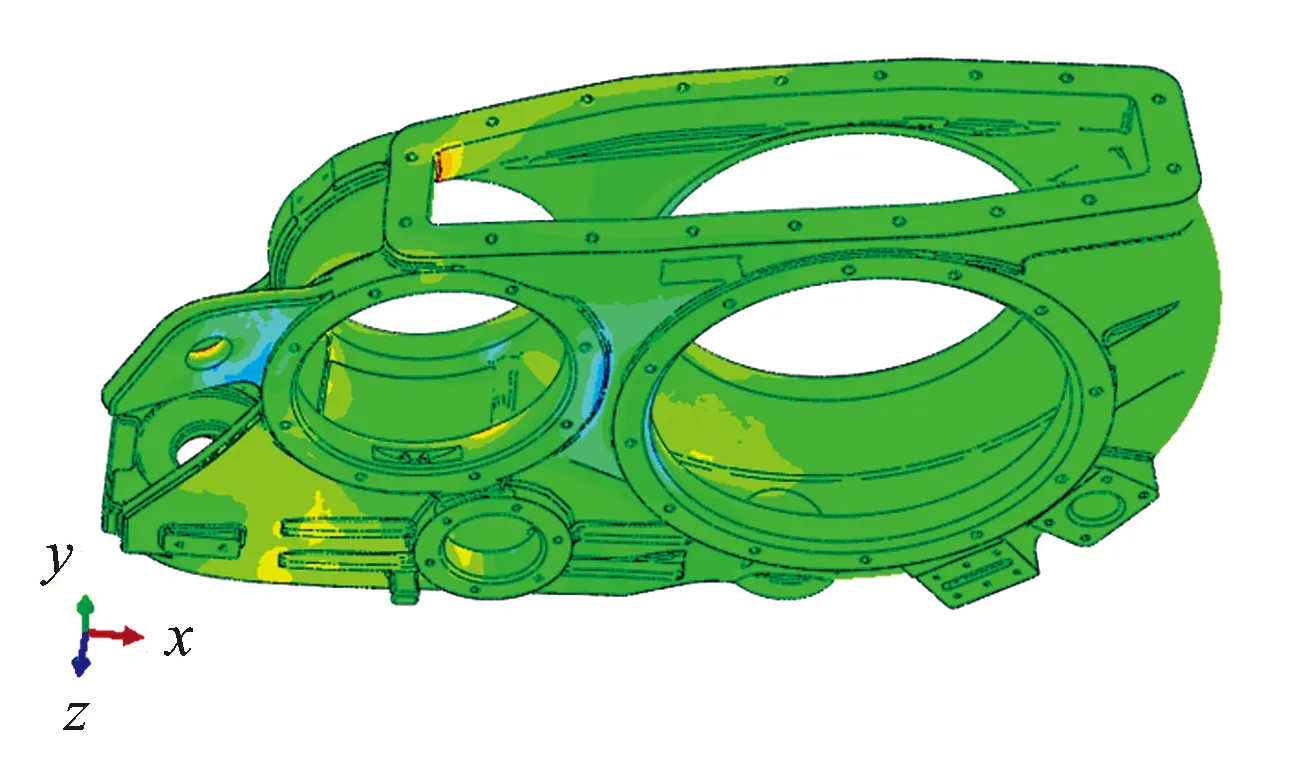
图7 第1阶约束模态响应

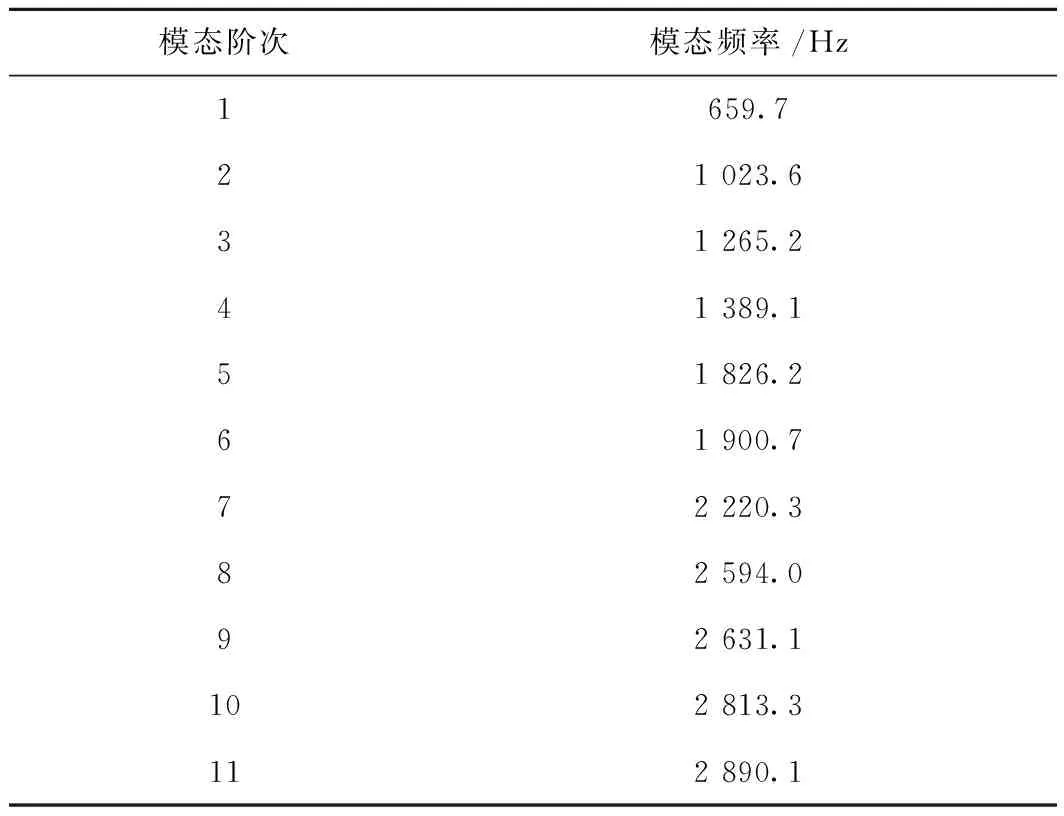
模态阶次模态频率/Hz1659.721023.631265.241389.151826.261900.772220.382594.092631.1102813.3112890.1

按照2.1节所述方法选择适宜的测试候选区，如图8所示，去掉所有不适合粘贴应变片位置(包括箱盖、吊杆、铭牌、轴承盖等附近)。选择22个测点估计箱体的前11阶模态参与因子，按照2.2节所述D优化得到测试候选区内测点最佳位置和方向，图8给出了由优化得到测点G&1～G&22的优化测点组。

图8 箱体测试候选区及优化测点组测点

图9所示为箱体优化测点组测点G&1～G&22前11阶模态应变矩阵。

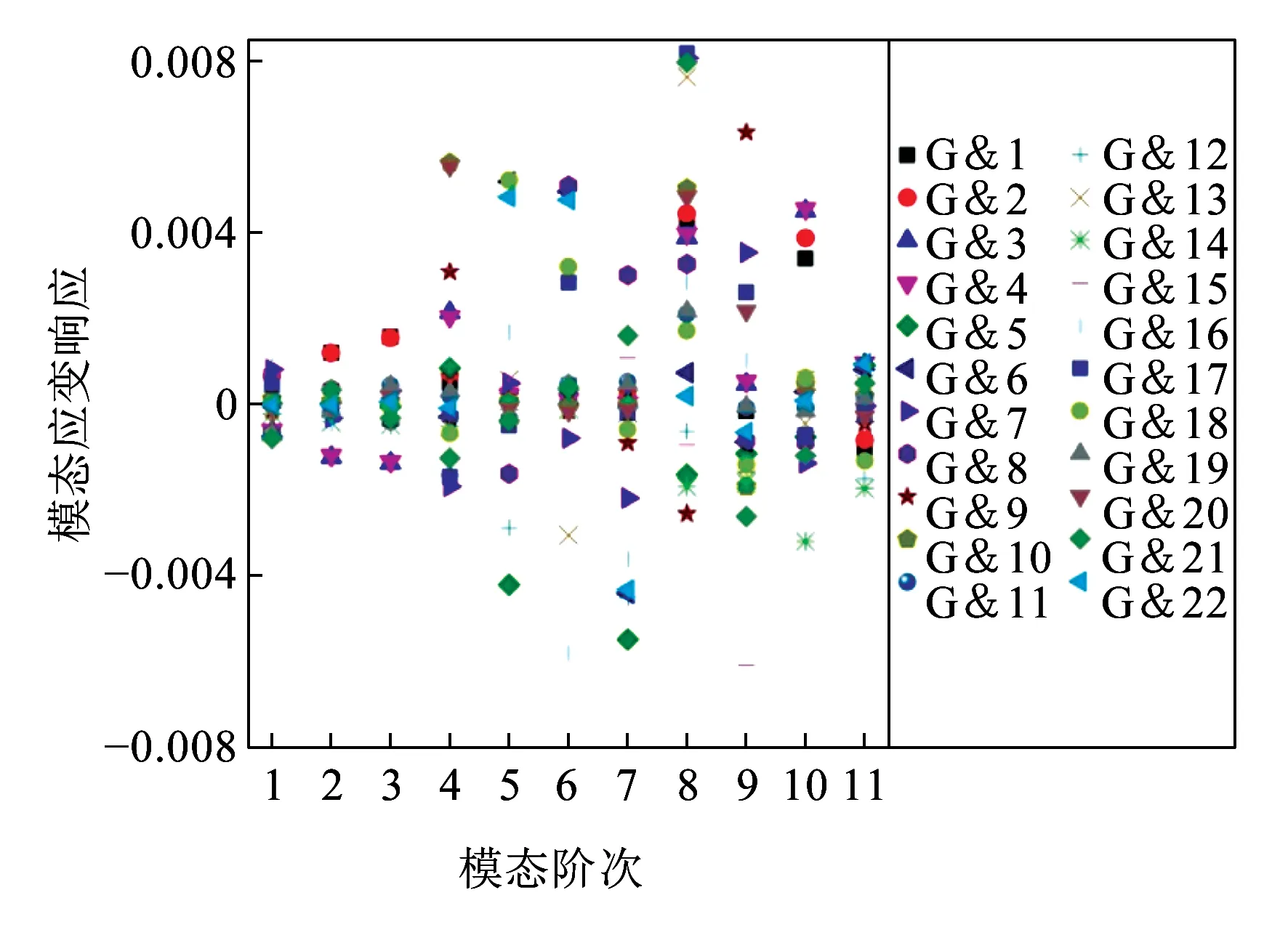
图9 箱体各测点前11阶模态应变矩阵

4.2 箱体模态参与因子识别

高速列车齿轮传动系统通常采用斜齿轮单级传动，轮齿啮合产生轴向力、径向力和垂向力，这三个方向的力由轴承传递给箱体。根据文献[15]齿轮箱箱体轴承载荷分布关系和文献[16]中运营工况下齿轮箱箱体载荷值，参考点RP3的纵向载荷幅值、垂向载荷幅值分别2 194、4 227 N，参考点RP4的纵向载荷幅值、垂向载荷幅值、横向载荷幅值分别2 194、4 227、3 077 N。对RP3和RP4按照上述对应载荷幅值加载动态扫频载荷，扫频范围为500～1 500 Hz，扫频时间为1 s，运用瞬态动力学仿真模拟，提取测点G&1～G&22应变响应。

实际测试和模拟仿真一般存在误差，如式(14)所示，对应变测点G&1～G&22理论值加15%的白噪声幅值误差进行模态参与因子估计，如图10所示。

εTest(t)=εth(t)+Δε(t)

(14)

式中：εTest(t)为实际测量应变响应；εth(t)为理论应变响应；Δε(t)为误差应变。

图10 测点G&1理论应变响应波形和15%白噪声幅值误差波形

根据式(13)，运用最小二乘法估计各阶模态参与因子，如图11所示(GU1为仿真波形，MPF1为识别波形)。表4给出15%应变幅值误差的各阶模态参与因子理论值和反求值拟合相关性及RMS误差。

图11 第1阶模态参与因子波形及散点图

模态阶次模态参与量/%斜率k拟合优度r2RMS误差/%180.1600.99980.99961.03211.8000.99990.99593.6646.9500.99960.99812.1831.0101.00040.953711.94100.0700.99860.96809.2850.0041.00120.923622.0760.0031.00100.942418.9570.0021.00000.904224.75801.00420.3822130.2590.0011.00090.97008.801101.01520.0920171.50

由表4可知，第1、2、4阶模态参与量之和占总模态的98.91%，模态参与因子的识别波形与理论波形之间RMS误差较小，第3、10阶模态参与量之和占总模态1.08%，模态参与因子的识别信号与理论信号的RMS误差不超过12%；第5、6、7、8、9和11阶模态的模态参与量之和占总模态的0.01%，对结构振动贡献量较少，即使RMS误差较大，对结构应变响应的能量贡献较小，可以忽略。

箱体的第1、2、4阶模态可以表达结构的整体振动特征，通过本文提出的方法可以准确识别结构振动的主要模态参与因子，说明运用有限测点测试可以识别箱体整体结构特征。

5 结论

本文提出了一种基于优化结构表面应变测点实现结构振动模态参与因子的时域识别方法，结合模态应变响应矩阵，可以获得结构整体响应。文中将悬臂梁板作为研究对象，选择6个应变测点对25～300 Hz的扫频信号进行前3阶模态参与因子时域波形估计，由模态叠加反求的两验证测点应力的RMS误差值较小，说明该方法模态参与因子估计准确度高。

对高速列车齿轮箱箱体进行小齿轮轴承座位置500～1 500 Hz扫频仿真，选择22个测点的仿真应变响应并对每个测点加15%的白噪声幅值误差，根据模态叠加基本原理，结合模态应变响应，运用最小二乘法估计前11阶模态参与因子时域波形，其中，模态参与量总和为98.9%的第1、2、4阶模态参与因子估计的RMS误差最大为3.66%，而其他阶模态参与因子虽然误差较大，但模态参与量较小，对结构振动响应误差较小，箱体的模态参与因子识别效果好。

参考文献：

[1]王萌,李强,孙守光.基于应力响应的多频率激励载荷识别研究[J].铁道学报,2015,37(2):27-33.

WANG Meng,LI Qiang,SUN Shouguang.Study of Multi-frequency Exciting Load Identification Based on Dynamic Stress Response[J].Journal of the China Railway Society,2015,37(2):27-33.

[2]姚起杭,姚军.工程结构的振动疲劳问题[J].应用力学学报,2006,23(1):12-15.

YAO Qihang,YAO Jun.Vibration Fatigue in Engineering Structure[J].Chinese Journal of Applied Mechanics,2006,23(1):12-15.

[3]ZHU N,SUN S,LI Q,et al.Theoretical Research and Experimental Validation of Elastic Dynamic Load Spectra on Bogie Frame of High-speed Train[J].Chinese Journal of Mechanical Engineering,2016,29(3):498-506.

[4]邹骅,李强,孙守光.基于载荷标定的城际列车转向架载荷及应力分布特征研究[J].铁道学报,2016,38(10):27-33.

ZOU Hua,LI Qiang,SUN Shouguang.Study on Intercity Train Load Spectrum Distribution Estimation and Calibration Methods Based on Load Demarcation[J].Journal of the China Railway Society,2016,38(10):27-33.

[5]FU D,WANG W,DONG L.Analysis on the Fatigue Cracks in the Bogie Frame[J].Engineering Failure Analysis,2015,58:307-319.

[6]王文静,惠晓龙,马纪军.高速列车设备舱支架疲劳裂纹机理研究[J].机械工程学报,2015,51(6):142-147.

WANG Wenjing,HUI Xiaolong,MA Jijun.Fatigue Crack Mechanism Research on High Speed Train Equipment Cabin Frame[J].Journal of Mechanical Engineering,2015,51(6):142-147.

[7]廖芳,高卫民,王承,等.基于模态扩展的变速器箱体振动识别及辐射噪声优化[J].同济大学学报:自然科学版,2012,40(11):1698-1703.

LIAO Fang,GAO Weimin,WAN Cheng,et al.Vibration Identification of Gearbox Housing by Modal Expansion and Radiation Sound Optimization[J].Journal of Tongji University:Natural Science,2012,40(11):1698-1703.

[8]张方,秦远田.工程结构动载荷识别方法[M].北京:国防工业出版社,2011.

[9]克雷格.结构动力学[M].常玲,李振邦,译.北京:人民交通出版社,1996.

[10]RAO S S.Mechanical Vibrations[M].5th ed.New Jersey:Prentice Hall,2010.

[11]CHATTERJEE S,HADI A S.Sensitivity Analysis in Linear Regression[M].New Jersey:John Wiley,1988.

[12]MITCHELL T J.An Algorithm for the Construction of D-optimal Experimental Designs[J].Technometrics,2000,16(2):203-210.

[13]GUPTA D K,DHINGRA A K.Input Load Identification from Optimally Placed Strain Gages Using D-optimal Design and Model Reduction[J].Mechanical Systems & Signal Processing,2013,40(2):556-570.

[14]GALIL Z,KIEFER J.Time and Space-saving Computer Methods,Related to Mitchell’s DETMAX,for Finding D-Optimum Designs[J].Technometrics,1980,22(3):301-313.

[15]黄冠华.高速列车齿轮传动系统动态特性研究[D].成都:西南交通大学,2015.

[16]STREET T,LONDON E C.GMRT2100:Railway Group Standard-requirements for Rail Vehicle Structures PartⅡ[S].2012.